Some subordination results for certain class with complex order defined by Salagean type q-difference operator

Let A denote the class of functions of the form:

∞ f (z) = z + ^ ak zk,                               (1.1)

k =2

which are analytic in the open unit disc U = {z E C : | z | < 1 } . We also denote by K the class of functions f ∈ A that are convex in U. For two functions f and g, analytic in U, we say that f is subordinated to g in U, written f (z) ^ g (z), if there exists a Schwarz function w (z), which (by definition) is analytic in U with w (0) = 0 and | w (z) | < 1, such that f (z) = g (w (z)) , z E U. Furthermore, if the function g is univalent in U, then (see [1, 2])

^{f (z)} ^ g^(z) ^ ^{f (0)} = g^{(0) and f ( U ) C} g^{( U )}.

Given two functions f, g G A , where f is given by (1.1) and g is given by

∞

g(z) = z + ^bk z^k , k=2

(1.2)

the Hadamard product (or convolution ) f * g is defined by

∞

(f * g) (z) = z + f akbk z ^k = (g * f) (z).

k =2

For 0 < q < 1, the q - derivative of a function f G A is defined by (see [3-9])

D q f(z) =

f ‘ (0), f ( qz )- f (z)

(q-1)z ^,

z = 0, z = 0,

(1.3)

and Dqf (z) = D q (D q f(z)). From (1.3), we have

∞

Dqf (z) = 1+^[k^q k =2

k-A akz    ,

(1.4)

where

Ml = 11

q ^{k q}

1 + q + q ²

+ . . . + q ^{k - l} ,

(1.5)

and

n \         f(qz) — f(z)        \ lim Dqf (z) = lim --7----7Г---- = f (z), q zl                q zl (q — 1)z for a function f which is differentiable in a given subset of C.

For f G A , Govindaraj and Sivasubramanian [10] defined the Salagean type q-difference operator as follows:

^D 0 ^{f (z)} = ^{f (z)},

D\f (z) = zDqf (z) = z + ^[k]q akzk, k=2

Dqf (z) = zDq (D l f (z) ) = z + f; ([k] q ) ² ak z^k , D qn f (z) = zDq ( nn ^-1 f (z) ) , n G N = { 1, 2, 3,... } .

It is easily see that

∞

Dqf (z) = z + f ([k] q ) ⁿ akz^k,  n G N o = N U { 0 } .

(1.6)

k=2

We note that lim Dnf (z) = Dnf (z) = z + f kn akzk,  n G No.

k=2

The differential operator D ⁿ was introduced and studied by Salagean [11] (see also Srivastava and Aouf [12]).

Let Gn (A, b, A, B) denote the subclass of A consisting of functions f (z) which satisfy

1 + H⁽1 — ^A) D n f^z) + ^AD q ( D n f (z) ) — 1] ^ 1 + A U                                        +z

(1.7)

or satisfying

(1 — A) f- + AD q ( D n f (z) ) — 1

f ) + ADq ( D n f (z))] — [B + (A — B) b]

<

1,

(1.8)

b E C * = C \{ 0 } ; 0 ^ A ^ 1; — 1 ^ A

z ∈ U.

We note that:

(i) lim Gn (A, b, A, B) = Gⁿ (A, b, A, B) (see [13]) q '■

= p E A : ¹ + b

(1 — A) Dn^z-M + A (D n f (z)) ’ —

1 + Az ^ 1 + Bz

}

;

(ii)

lim Gn (A, b, 1, — 1) = Gⁿ (A, b) (see [14]) q '■

= p E A : R (1 + b [(1 - A)

D f    + A (D n f (z)) ’ — 1]) > 0^

;

(iv)

(v)

(vi)

(vii)

G (A, b, A, B)= G_q (A, b, A, B)

= p ^E A ^{: 1 +} b

(1 — A) fzz)

G qn (A,b, — 1, 1)= G qn (A,b)

D ⁿ f (z)

= p E A : R (1 + b (1 — A) -q^

G _q ⁿ (0, 1 — a) = G _q ⁿ (a) = f E A : R

G qⁿ (0, 1

G qⁿ (A, 1

D qⁿ f (z)

z

-

-

G qⁿ λ, e

⁺  '• ^f <^z) - ^l] ^ r+A}

+ AD q ( D n f (z) ) - 1] } > 0^

> a, 0 <  a <  p ,

a) = R n (a) = {f E A : R [D q DDff (z)] > a, 0 ^ a < 1} ;

a, — 1,1)= G qn (A, a)

= p E A : R (1 - A)

D n f (z)

z

+ ADq ( D n f (z) ) >a},

-

i⁶ (1 — a) cos 9, — 1,1 ) = Gn (A, a, 9)

;

;

0 ^ a < 1;

= p E A : R (e i⁶ [(1 — A) Dq^zM + AD q ( D n f (z))] ) > a cos 91,

| 9 | < П, 0 ^ a < 1.

2.    Main Result

To prove our main result we need the following definition and lemmas.

Definition 1 (Subordinating Factor Sequence [15]). A sequence {bk } k=i of complex numbers is said to be a subordinating factor sequence if, whenever f (z) of the form (1.1) is analytic, univalent and convex in U, we have the subordination given by

∞

5 akbk z k ^ f (z), z £ U, a i = 1.

k=1

Lemma 1 [15] . The sequence {bk } k=i is a subordinating factor sequence if and only if

R

{1+2 E b k = k}

> 0,

z ∈ U.

Now, we prove the following lemma which gives a sufficient condition for functions to belong to the class Gn (A, b, A, B).

Lemma 2. Let the function f which is defined by (1.1) satisfy the following condition:

∞

E (1 + B ) {1 + A ([k] , - 1)} ([k],)" | a k | < (B - A) | b | ,              (2.1)

k=2

then f £ Gn (A, b, A, B) .

• <1 Suppose that the inequality (2.1) holds. Then we have for z £ U,

D ⁿ f (z)

(1 - A) -qiu + ad , ( Df (z) ) - 1

Г         D n f (z)

B (1 - A) -qiu + ad , ( Df (z) )

- B - (A - B ) b

∞

E{ 1 + A ([k], - 1)}([k],)"ak zk-i k=2

∞

(B - A) b + B £ {1 + A ([k] , - 1) } ([k],) " ak z ^{k- i} k =2

< V { 1 + A ( [k] , - 1 )}( [k] , ) " | akHz | ^{k- i} k=2

• - | (B - A) | b | - B £ { 1 + A ( [k] , - 1 ) } ( [k] , ) " | a k | | z | ^{k- i} I k=2

∞

< £ (1 + B) {1 + A ([k], - 1)} ([k],)“ |ak| zk-i - (B - A) |b| < 0, k=2

which shows that f (z) belongs to the class Gn (A, b, A, B). >

Let Gn * (A, b, A, B) denote the class of functions f (z) £ A whose coefficients satisfy the condition (2.1). We note that Gn * (A, b, A, B) C Gn (A,b, A, B). Also, let G. (A, b, A, B) = G * (A,b,A,B), GП * (A,b, - 1,1) = GП * (A,b), Gn * (A, 1 - a, - 1,1) = Gn * (A, a), Gn * ( A,e ^-i6 (1 - a) cos 0, - 1,1 ) = Gn * (A,b,0) ( | 0 | <  ^п , 0 ^ a < 1 ) .

In this paper we prove several subordination relationships involving the functional class Gn* (A,b, A, B) employing the technique used earlier by Attiya [16] and Srivastava and Attiya [17] (see also [13, 14, 18–22]).

Theorem 1. Let the function f defined by (1.1) be in the class Gn* (A, b, A, B) and g ∈ K . Then

У (1 + b ) (1 + Aq) (1 + q) ⁿ            / f w f \

(2 [(1 + B)(1 + Aq) (1 + q) ⁿ + (B - A) | b | ]) ^(f * g) ^(z) ^ g ^{(z)           ( )}

(L+BH^+^^i+syn+SB-AiM.

R {f ^(z)} >          (1+ B)(1 + Aq) (1 + q) ⁿ        ’ z ^e U’           ^{( )}

qq t ne constant factor 2[(1+B)(1+Aq)(1+€i)n+(B A)|b|] in the subordination result (2.2) cannot be replaced by a larger one.

< Let f E Gn* (A, b, A, B ) and let g (z) = z + £ ckz^k E K . Then we have k=2

(      (1+^{B H1}+^Na+q) ⁿ

V2 [(1 + B)(1+ Aq) (1 + q) ⁿ + (B - A) \b\]) ^(J g⁾⁽ )

-(

(1 + B )(1 + Aq)(1 + q) n

2 [(1 + B)(1+ Aq)(1 + q) ⁿ + (B - A) | b | ]

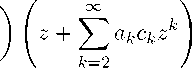
(2.4)

Thus, by Definition 1, the subordination result (2.2) will hold true if the sequence

■ . B ■ . >q ■ . q

^{(1+ b ) (1+Aq) (1+}q^{) n + (}B - ^A) | b | ^k) k=i

(2.5)

is a subordinating factor sequence, with a i = 1. In view of Lemma 1, this is equivalent to the following inequality:

^ / 1 + ^E_____ ^{(1+ B)(1+ Aq)(1 + q}T ______o /1 > ₀ G U (2 6)

R k= (1 + b)(1 + Aq)(1 + q) ⁿ + (b — a) \ b l a k zi> ⁰ z^EU’      ^{( )}

Since

ф(к) = |1 + a ([k]q - 1)}([k]q)n , k > 2, 0 ^ A ^ 1, 0

{DC

1+E k=i

(1+ B)(1+ Aq)(1 + q)n

(1 + B )(1 + Aq)(1+ q)ⁿ+ (B - A) |b|

akz^k

₌ U i ₊      (1 + B)(1 + ^Aq)(1 + q)ⁿ      .

1 ⁺(1 + B )(1 + Aq)(1+ q)ⁿ+ (B - A) |b|

∞

+

(1 + B) £ (1 + Aq)(1+ q)n k=2

(1+ B)(1+ Aq)(1 + q)n + (B

-

A)|b|“^kzk}

> 1 -

(1+ B)(1+ Aq)(1 + q)n

>1

(1+ B)(1+ Aq)(1+ q)n + (B - A) |b| r (1 + B )(1 + Aq)(1+ q)n

-

-

(1 + B )(1 + Aq)(1+ q)n + (B - A) |b| r

k£ (1 + B){1 + A ([k]q - 1)}([k]q)n |ak| (1 + B )(1 + Aq)(1+ q)ⁿ+ (B - A) |b| r

(B - A) \b|

-

(1+ B)(1+ Aq)(1+ q)n + (B - A) |b| r

= 1 - r > 0,   |z| = r < 1, where we have also made use of assertion (2.1) of Lemma 2. Thus (2.6) holds true in U and also the subordination result (2.2) asserted by Theorem 1. The inequality (2.3) follows from (2.2)

by taking the convex function g (z) = y-z = z + ^k= zk• To prove the

constant by

(1+B)(1+Aq)(1+q)ⁿ

2[(1+B)(1+Aq)(1+q)n+(B-A)|b|]

, we consider the function fo (z) € Gn*

sharpness of the (A, b, A, B) given

Thus from (2.2), we have

г / \ _              (B — A) |b|          2

f^{0 (z)} =^{z —} (T+B)a"+^Aqya"+^f^z.

(2.7)

(1 + B )(1 + Aq)(1+ q)n

2 [(1 + B)(1 + Aq) (1 + q)n + (B - A) |b|]

^f0 ^(z)^ 1

z

-

, z

z ∈U.

(2.8)

Moreover, it can easily be verified for the function fo (z) given by (2.7) that

min < R f

|z|Cr I V

(1+ B)(1+ Aq)(1 + q)ⁿ

2 [(1 + B) (1 + Aq) (1 + q)ⁿ+ (B — A) |b|]

^{fo (z)})}=- 2

.

(2.9)

This shows that the constant the proof of Theorem 1. >

(1+B)(1+Aq)(1+q)ⁿ

2[(1+B)(1+Aq)(1+q)ⁿ+(B-A)|b|]

is the best possible, this completes

Putting n = 0 in Theorem 1, we have

Corollary 1. Let the function f defined by (1.1) be in the class G* (A, b, A, B) and g € K. Then

/        (1 + B )(1 + Aq)        A _             .

(2[(1+ B)(1+ Aq) + (B - A) |b|]J ^(f* g^)(z)^ g ^(z) ’ z ^€ U’

(2.10)

and

- ^{(1 + B)(1 + Aq) + (B — A) |b|}

R{f (z)} >        (1+ B)(1+ Aq)

.

(2.11)

The constant factor 2[(1+B)(1+Ay)+(B A)|b|] in the subordination result (2.10) cannot be rep laced by a larger one.

Putting A = -1 and B = 1 in Theorem 1, we have

Corollary 2. Let the function f defined by (1.1) be in the class Gqn* (A, b) and g € K.

Then

/    ^{(1 +} A^{q) (1 + q)}

V 2 [(1 + Aq)(1 + q)n

n

+ |b|]

) ^(f* g)^(z)^ g^(z), z ^€ U

(2.12)

and

R{f (z)} >

-

(1 + ^AqlO + 9r±Ibl

(1 + Aq)(1+ q)ⁿ’ z^€ U

(2.13)

The constant factor by a larger one.

(1+Aq)(1+q)ⁿ

2[(1+Aq)(1+q)ⁿ+|b|]

in the subordination result (2.12) cannot be replaced

Putting b = 1 — a(0 C a < 1), A = —1 and B = 1 in Theorem 1, we have

Corollary 3. Let the function f defined by (1.1) be in the class Gn* (A, a) (0 C a < 1) and g ∈ K . Then

n

/      ^{(1 + Aq) (1 + q)}

\^{2 [(1 + Aq) (1 + q)n + 1}

-

—г) (f * g)(z) ^ g(z), z € U aU

(2.14)

and

тг/мт. ^{(1 + Xq)} (1 ^{+ q)}n + 1 ^{— a} c

R^{f (z)} >       _{(1+ A}q_{)(1 +}q)n    , z ^E U               ⁽².1⁵⁾

(1+^q)(1+q)n

in the subordination result (2.14) cannot be replaced

The constant factor 2[(1+Aq)(1+q)n+1-a] by a larger one.

Putting b = e i⁶ (1 — a) cos 6 (|6| < П; 0 C a < 1) , A = —1 and B = 1 in Theorem 1, we have

Corollary 4. Let the function f defined by (1.1) be in the class Gn* (X-a-G} (|6| < П; 0 C a < 1) and g E K. Then

n

2 .. ,_: +.     T.    .       )*»^)(z)"»«- ^zEU-       ^(2Л6)

and

R f «} > — ^(1±X7r++f^^- ZE U.       (2.17)

C^+^q^C^+q)

The constant factor 2[(1+Aq)(1+q)n+(1-a) cos6] replaced by a larger one.

in the subordination result (2.14) cannot be

Remark 1. Taking A = — 1, B = 1 and letting q ^ 1 in Theorem 1, we get the result obtained by Aouf [14, Theorem 1].

Remark 2. Replacing A by —A, B by —B and letting q ^ 1 in Theorem 1, we obtain the result get by Sivasubramanian et al. [13, Theorem 2.2].

Remark 3. Putting n = Х = 0, b = 1 — а (0 C а < 1) and letting q ^ 1- in Corollary 2, we get the result obtained by Aouf [14, Corollary 3].

Remark 4. Putting n = 0, Х = 1, b = 1—a (0 C а < 1) and letting q ^ 1- in Corollary 2, we get the result obtained by Aouf [14, Corollary 4].