Соотношение структурных показателей речных бассейнов Верхнего Приангарья

Введение. Изучая структуру речного бассейна, как геоморфологической и природной системы, мы выявляем основные закономерности распределения потоков вещества в пространстве и времени на различных иерархических уровнях. Цель исследования — выявление структуры речных бассейнов Верхнего Приангарья, на примере модельного объекта бассейн реки Оек (приток р. Куды).

Объект и методы исследования. Бассейн р. Оек расположен в пределах нескольких геоморфологических районов. Его северная часть, включающая бассейны рек Рассошина и Молька, находится в пределах Лено-Ангарского плато

[1]. Восточная часть бассейна (реки Хуширей-Гол и Кударейка) относятся к Ку-динской депрессии Предбайкальского прогиба. Его южная часть входит в область Присаянского краевого прогиба, выполненного Иркутско-Черемховской равниной.

Бассейн реки Оек вытянут в субмеридиональном направлении, а его площадь составляет 600 км2 (рис. 1). Ширина бассейна увеличивается от 10 км в верхнем течении до 23 км в среднем за счет бассейна р. Уня. Плотность эрозионного расчленения изменяется в интервалах 1,3-1,4 км/км2. Большая часть бассейна р. Оек лежит в пределах распространения юрских песчаниковых и песчаниковогалечниковых отложений.

Река относится к группе рек с недостаточно обеспеченным стоком, а также характеризуется промерзанием русла в зимний период, сокращением стока в летний период, значительными мутностью и температурами в летний период [2].

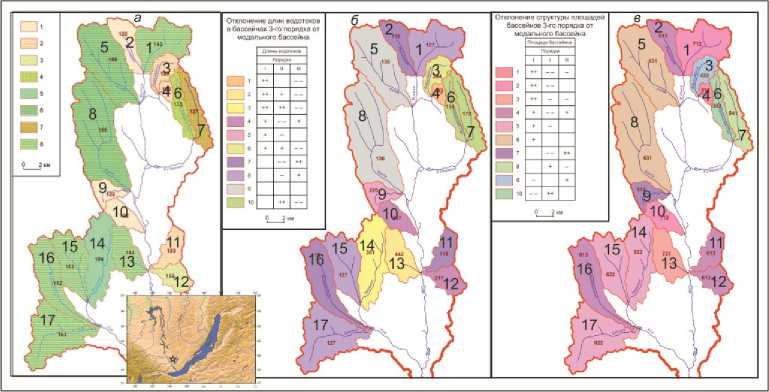
Рис. 1. Картосхема распределения индексов структуры бифуркации и длин для подбассейнов 3-го порядка бассейна р. Оек: а — картосхема распределения индексов структуры бифуркации в подбассейнах 3-го порядка бассейна р. Оек. Бассейны с простой структурой : 1 — с минимальным количеством водотоков. Бассейны с упрощенной структурой : 2 — с минимальным количеством водотоков 2-го порядка; 3 — с минимальным количеством водотоков 1-го порядка. Бассейны со структурой близкой к модальной: 4 — с пониженным количеством водотоков 1-го порядка. Бассейны с усложненной структурой : 5 — с высоким количеством водотоков 2-го порядка. Бассейны со сложной структурой : 6 — с высоким количеством водотоков 1-го и 2-го порядков. Бассейны смешанного типа : 7 — с высоким количеством водотоков 1-го порядка и низким количеством 2-го; 8 — с низким количеством водотоков 1-го порядка и высоким количеством 2-го; б — картосхема распределения индексов структуры длин для подбассейнов 3-го порядка бассейна р. Оек. в — картосхема распределения индексов структуры площадей для подбассейнов 3-го порядка бассейна р. Оек. Цифрами от 1-17 обозначены номера бассейнов (совпадают с нумерацией в таблицах), индексы структуры обозначены трехзначными числами. Во врезке знаком звездочка обозначен бассейн р. Оек.

В формировании рельефа кроме флювиального, активно принимают участие процессы карстообразования и криогенеза, которые во многом обусловили особенности формирования современного облика речных долин. Наиболее подвержен процессам карстообразования бассейн р. Заельник, а полигональный криогенный рельеф ярко представлен в бассейне р. Барды.

Для анализа бассейна использовался методический подход, основанный на морфометрическом анализе речных бассейнов (Хортон-анализ) [7-11]. Суть системы кодирования водотоков Стралера-Философова [7] заключается в том, что водоток (или русло временного водотока), не получающий притоков, относится к руслам 1-го порядка, два русла 1-го порядка при слиянии образуют русло 2-го порядка и т. д.. Анализ речных бассейнов широко применяется при геоморфологических и гидрологических исследованиях как в нашей стране [8-11], так и за рубежом [3,4]. Детально проработан и значительно усовершенствован для геоморфологических исследований он был в работах Ю. Г. Симонова, В. В. Кружалина и Т. Ю. Симоновой [9-11], в которых для анализа речных бассейнов был предложен ряд структурных индексов.

Анализ бассейнов проводился с помощью структурных индексов [8, 9], выражающих соотношение морфометрических характеристик разнопорядковых водотоков в бассейнах третьих порядков. Для каждого индекса бассейнов третьего порядка в работах [8, 9] рассчитаны модальные индексы, которые не зависят от генетической, структурно-тектонической, литологической, ландшафтногидрологической составляющих и рассматриваются в качестве эталонных. 1) Индекс структуры бифуркации (ИСБ), выражает соотношение количества разнопорядковых водотоков в бассейнах третьего порядка. Модальный индекс равен 134, где 1 — количество водотоков третьего порядка; 3 — количество водотоков второго порядка; 4 — количество водотоков первого порядка на каждый водоток второго.

• 1)    Индекс структуры длин (ИСД) показывает соотношение средних длин водотоков разных порядков — в модальном показателе ИСД=136, первая цифра показывает, что средние длины водотоков первых порядков составляют около 10 %, длины — вторых порядков — 30 %, длины третьего порядка — 60 %.

• 2)    Индекс структуры площадей (ИСП) выражает соотношение средних площадей разнопорядковых бассейнов. Модальный ИСП составляет 532 и означает, что в бассейне 3-го порядка 50% занимают водосборы первого порядка, 30% — площади склонов, опирающиеся на притоки второго, 20% — площади склонов, опирающиеся на притоки третьего порядка.

• 3)    Индекс структуры уклонов (ИСУ) выражает соотношение средних уклонов (уклон — тангенс угла наклона) разнопорядковых водотоков в бассейне в процентном соотношении, где 100% — сумма средних уклонов в бассейне. Модальный индекс равен 631, где первая цифра — 60%, приходится на уклоны водотоков первого, 30% — второго, 10% — третьего порядка.

• 4)    Геоморфологическая работа водотоков (М) — отношение индекса структуры площадей к индексу бифуркации бассейна, выражается в разделении площадей определенного порядка на число водотоков соответствующего порядка и позволяет определитьнагрузку на единичный водоток. Модальное значение для

бассейнов третьего порядка составляет 6:3:1, то есть нагрузка на водоток первого порядка составляет 6, второго –3, третьего — 1.

Расчет, согласно методическим указаниям, проводился для следующих индексов (табл. 1). Дополнительно для анализа морфометрических структурных характеристик бассейнов использовались коэффициенты, широко применяемые зарубежными исследователями [3-7] (табл. 2).

В качестве исходных данных использовалась цифровая модель SRTM v.4 с разрешением 3 угловых секунды, доступная на сайте консорциума CGIAR-CSI . Обработка исходных данных производилась в открытой настольной ГИС SAGA . Цифровая модель SRTM была пере-проецирована в прямоугольную систему координат и подвергнута гидрологической коррекции, при которой были заполнены локальные бессточные впадины. С помощью модулей гидрологического анализа была выделена эрозионная сеть и элементарные бассейны, получены их высотные характеристики. Дальнейшая обработка данных проводилась в векторном формате в программной среде ГИС MapInfo Professional. Полученная эрозионная сеть была скорректирована по топографическим картам масштаба 1:50 000, определены морфометрические характеристики водотоков и их бассейнов — длины, площади, уклоны, показатели расчлененности, ряд морфометрических и структурных параметров.

Результаты исследования и обсуждение. Структурные индексы подбассейнов третьего порядка. Порядок р. Оек, рассчитанный по системе Стралера-Философова составляет 5 [7, 9]. Для структурного анализа по методике Ю. Г. Симонова [8, 9] используются показатели бассейнов третьего порядка. В бассейне р. Оек выделено 17 подбассейнов третьего порядка, 10 из них расположены в правобережной части бассейна (табл. 1).

Таблица 1

Структурные индексы подбассейнов 3-го порядка бассейна р. Оек

Название и номер водотока третьего порядка	Структурные индексы					Пло щадь, 2 км2
	бифуркации (ИСБ=134)	площадей (ИСП=53 2)	уклонов (ИСУ=63 1)	длин (ИСД=13 6)	геоморфологическая работа (М=6:3:1)
Верхнеленское плато
Водотоки 3 порядка бассейна р. Оёк
Подбассейны водотоков 3-го порядка бассейна р.Мольки (левый приток р. Оек)
1. р. Моль-ка (до устья Рас-сошины)	143	712	541	127	6:3:1	26,01
2. р.  Рас- сошина	122	613	712	118	5:1:1	14,05
Кудинская депрессия (Предбайкальский прогиб)
Подбассейны водотоков 3-го порядка бассейна р. Барходайка (левый приток р. Оек)
3. р.  Бар- ходайка	123	433	631	244	5:2:2	9,67
4. р. Мостки	123	811	523	433	6:2:3	3,34

Подбассейны водотоков 3-го порядка бассейна р. Кударейка (левый приток р. Оек)
6. р. Хурши-рей-Гол (правый приток р. Куда-рейка)	133	352	532	154	2:2:1	10,53
7. р. Куда-рейка    (до устья      р. Хурширей-Гол)	127	541	631	172	6:3:1	14,96
Иркутско-Черемховская равнина (Присаянский прогиб)
Подбассейн 3-го порядка правого притока р. Оек
5. р. Оечек	155	631	631	136	10:6:1	41,26
Водотоки бассейна р. Барда (правый приток р. Оек)
8. р. Барда	155	631	721	136	10:6:1	57,99
9. Правый приток р. Барды (ур. Буржин)	122	514	631	226	7:3:2	8,33
Притоки р. Оек
10. Правый приток р. Оек (падь Загунтуй)	122	712	631	217	6:2:1	10,01
11. Левый приток р. Оек (падь Черемуховая)	123	613	361	118	5:5:1	10,67
12. Левый приток р. Оек (падь Глубокая)	132	613	532	217	7:3:2	9,98
13. Правый приток р. Оек (падь Скулина)	142	721	631	442	3:1:2	16,9
Водотоки бассейна р. Уня (правый приток р. Оек)
14. р. Заель-ник (левый приток р. Уня)	154	622	631	361	2:1:3	29,65
15. р. Уня	153	622	631	127	10:6:1	23,37
16. р. Моза-линская (правый приток р. Уня)	152	613	631	118	6:2:1	26,35
17. р. Елкина	163	622	631	127	7:3:2	36,4

Рассчитанные индексы структуры бифуркации (ИСБ), выражающие соотношение количества разнопорядковых русел в бассейнах третьего порядка отклоняются от модального значения. Анализ пространственного распределения показал, что западная часть территории исследования наиболее расчленена в пределах средних звеньев эрозионной сети, исключая небольшие по площади подбассейны. Тогда как для бассейнов, расположенных в восточной части, характерно снижение количества водотоков второго порядка по сравнению с модальными (рис. 1, а). В то же время бассейны с небольшой площадью обладают простой структурой бифуркации, тогда как вариативность распределения русел разных порядков возрастает с площадью подбассейнов.

Анализ распределения структурного индекса длин выявил два бассейна с модальным показателем (ИСД=136) — реки Оечек (до устья р. Мольта) и р. Барда, которые обладают наибольшей площадью (рис. 1, б, табл.1). В целом для большинства бассейнов распределение средних длин близко к нормальному и характеризуется увеличением средних длин водотоков первого порядка и уменьшением длин водотоков второго порядка. В этих бассейнах скорость получения водотоком второго порядка падает, а третьего напротив — возрастает. Наиболее длинные водотоки второго порядка расположены в пределах Кудинской депрессии.

Анализ распределения структурного индекса площадей (модальный ИСП=532) показал, что в большинстве случаев площади бассейнов первого порядка больше, а второго — меньше модальных значений (рис. 1, в, табл.1). В бассейнах с максимальными площадями незначительно увеличены средние значения площадей бассейнов первого порядка, но уменьшены третьего.

Большинство значений структурного индекса уклонов (модальный ИСУ=631) бассейнов третьего порядка совпадают с модальным (табл. 1). Для двух бассейнов рек Барда и Рассошина (ИСУ соответственно 712 и 721) уклоны водотоков первого порядка незначительно повышены, уклоны водотоков второго порядка — понижены, третьего или соответствует модальному или повышены. Бассейн пади Черемуховая, напротив, обладает низким значением уклонов водотоков первого порядка, значения уклонов водотоков второго порядка повышены, а третьего — совпадают с модальным (ИСУ=361). Значения уклонов водотоков первого порядка незначительно понижены относительно модального, а уклоны второго и третьего порядков либо завышены, либо занижены (падь Глубокая; р. Молька, р. Мостки).

Динамические показтели подбассейнов третьего порядка. Распределение геоморфологической работы (М) в бассейнах третьего порядка. Интенсивность геоморфологической работы является результирующим показателем структуры бассейна, которая иллюстрирует нагрузку на водотоки разного порядка в бассейне. Этот показатель определяется уклоном, длиной и площадью для каждого водотока [2, 4-5]. В бассейне р. Уня показатели работы водотоков совпадают с модальным: для водотоков первого порядка равны 6, для водотоков второго порядка — 3, для водотоков третьего порядка — 1. Наибольшей нагрузкой на водотоки первого и вторых порядков отличаются бассейны рек Оечек, Барда и Уня (табл. 2). Бассейн р. Мостки также выделяется повышенной нагрузкой на водотоки первого порядка, однако здесь повышается нагрузка и на водоток третьего порядка (табл. 1).

Дополнительно для морфометрического структурного анализа бассейнов использовались следующие характеристики (табл. 2).

Параметр Rbm (Mean Bifurcation Ratio) — коэффициент среднего разветвления (бифуркации) водотоков всех порядков. Рассчитывается из среднего арифметического между соотношениями количества русел 1-го к 2-му и 2-го к 3-му порядков. Rbwm (Weighted Mean Bifurcation Ratio) — коэффициент средневзвешенного разветвления (бифуркации) водотоков всех порядков). Для получения этого коэффициента отношение длин (Rbwm) умножается на количество водотоков порядков, которые используется при расчете (отношение средних длин 2-го к 1-му порядку умножается на количество водотоков 1-го и 2-го порядков и т.д.).

Коэффициенты Rbm и Rbwm показывают хорошую корреляцию с таковыми ИСБ. Максимальные значения Rbm у бассейнов рек Молька. Кударейка, Оечек, Барда, Заельник, Елкина, вссе эти бассейны характеризуются также повышенными значениями ИСБ (табл. 1).

Коэффициент Lur (Stream Lenght Ratio) — отношение средних длин разнопорядковых водотоков). Рассчитывается Lur, как отношение средней длины одного порядка к средней длине следующего низшего порядка. Конечное значение составляет среднее арифметическое между отношениями средних длин вторых и первых и третьего и вторых порядков.

Коэффициент Luwm ( Weighted Mean Stream Length Ratio) — отношение средневзвешенных длин разнопорядковых водотока. Для получения этого коэффициента отношение длин (Lur) умножается на количество водотоков порядков, которые используется при расчете (отношение средних длин 2-го к 1-му порядку умножается на количество водотоков 1-го и 2-го порядков и т. д.). Наименьшие значения Luwm у бассейнов рек Мостки и Скулина, ИСД которых значительно отклоняются от модального и имеют значительно завышенные показатели средних длин русел 1-го и заниженные 3-го порядков. Максимальные значения Luwm в бассейнах рек Мозалинская. Загунтуй, Рассошина, значения их ИСД показывает завышенные значения для длин 3-го и заниженные — для длин 2-го порядков.

Arm (Mean Area Ratio) — отношение средних площадей разнопорядковых водотоков. Значение этого коэффициента представляет отношение средней площади одного порядка к средней площади следующего низшего порядка. Конечное значение составляет среднее арифметическое между отношениями средних площадей вторых и первых и третьего и вторых порядков. Arwm (Weighted Mean Area Ratio) — отношение средневзвешенных площадей разнопорядковых водотока. Для получения этого коэффициента отношение площадей (Lur) умножается на количество водотоков порядков, которые используется при расчете (отношение средних площадей 2-го к 1-му порядку умножается на количество водотоков 1-го и 2-го порядков и т. д.). Анализ значений этих коэффициентов и индекса структуры площадей (ИСП) для бассейнов 3-го порядка р. Оек показал значительное расхождение данных характеристик.

Подводя итог вышесказанному, можно отметить, что структурные индексы полнее показывают взаимосвязи морфометрических характеристик разнопорядковых русел (с дальнейшим выходом на динамические показатели) внутри бассейна, тогда как структурные коэффициенты целесообразней использовать для характе- ристики бассейнов в целом, так как информации о внутренней структуре бассейна они не несут.

Таблица 2

Структурные коэффициенты подбассейнов 3-го порядка бассейна р. Оек

Название и номер	Структурные коэффициенты
	Rbm	Rbwm	Lur	Luwm	Arm	Arwm
1. Молька	4,63	5,04	3,11	2,34	3,29	2,31
2. Рассошина	3,5	4,4	10,6	7,55	12,13	9,41
3. Барходайка	2,75	3,13	1,7	1,88	2,19	2,23
4. Мостки	2,5	2,73	0,85	0,9	0,78	0,63
5. Оечек	5,1	5,17	2,43	2,41	2,37	2,39
6. Хурширей-Гол	2,25	2,35	1,98	2,11	3,04	3,06
7. Кударейка	4,5	6,21	2,36	3,2	3,15	4,12
8. Барда	5,8	6,38	2,46	2,65	2,53	2,74
9. ур. Буржин	2,25	2,35	2,38	2,04	3,55	3,3
10. п. Загунтуй	3,25	3,96	9,3	5,98	16,92	9,97
11.п. Черемуховая	3,75	4,84	4,94	3,86	5,67	3,72
12.п. Глубокая	2,83	2,76	3,13	2,32	3,77	2,61
13. п. Скулина	3,38	3,06	0,71	0,88	1,19	1,03
14. Заельник	5,42	5,03	1,13	1,61	2,95	2,54
15. Уня	4,3	3,89	2,91	2,48	2,74	2,23
16. Мозалинская	4,1	3,6	11,29	9,05	15,76	12,6
17. Елкина	5,5	5,16	2,43	2,01	4,3	3,27

Выводы Сопоставление значений структурных коэффициентов и структурных индексов для бассейнов третьего порядка р. Оек проиллюстрировал их хорошую корреляцию (исключая параметры площадей). В целом, наибольшей однородностью показателей структурных индексов отличаются бассейны третьего порядка Иркутско-Черемховской равнины, сосредоточенные в юго-западной (притоки р. Уня) и северо-западной частях (реки Оечек и Барда) бассейна. Наибольшим разнообразием в распределении структурных индексов обладают бассейны Кудинской депрессии Предбайкальского прогиба. Максимальная работа по переносу вещества в бассейнах выполняется водотоками первого порядка в западной части бассейна р. Оек.