Совершенствование методов количественной интерпретации геопотенциальных полей

Состоятельность любого метода решения обратных задач геофизики определяется его адекватностью реалиям и целям геофизических исследований, открытостью к использованию различной априорной информации о помехах и источниках поля, наличием средств оценивания точности и достоверности собственных результатов. В полной мере удовлетворить этим требованиям могут лишь методы, сочетающие достоинства детерминистского и вероятностно-статистического подходов [5].

Как правило, присутствие какого-то одного из подходов в алгоритме решения обратной задачи носит вынужденный, безальтернативный характер, а не определяется какими-то методологическими соображениями. Так, в методах решения обратных задач гравиметрии и магнитометрии, относящихся к вероятностно-ста- тистическим, детерминированная составляющая представлена одной лишь процедурой вычисления поля от заданного распределения масс. В методах с преобладанием детерминированной составляющей аппарат теории вероятностей и математической статистики используется разве что для оценки уровня помех в измерениях поля, тогда как сами ограничения на допустимые значения невязки носят уже детерминистский характер. Собственно критерий выбора оптимального решения из множества допустимых при этом никак не привязан к вероятностным свойствам помех.

В число требований, которым должны удовлетворять новые алгоритмы решения обратных задач геофизики (помимо адекватности геофизический практике), целесообразно включить:

и робастность результатов интерпретации;

U использование как детерминистских, так и вероятностных приемов описания свойств случайных помех при ослаблении априорных предпосылок о законах их распределения;

U построение геологически содержательной оценки точности полученных результатов;

и сохранение всех возможностей детерминистского подхода в вопросах формализации априорных ограничений и описания множества допустимых решений обратной задачи [2].

Оценка достоверности результатов интерпретации данных гравиразведки и магниторазведки

Методологической основой для решения этой задачи служит гарантированный подход, вобравший в себя идеи из многих разделов прикладной математики, направленный на извлечение достоверной информации в условиях неопределенности и успешно зарекомендовавший себя в различных областях науки (прежде всего – в теории управления). Объектом исследования при гарантированном подходе являются многозначные отображения совокупной априорной информации в множества допустимых решений; при этом описание неопределенностей имеет вид включений неизвестных величин в некоторые множества.

Центральная идея гарантированного подхода была изложена еще в работе Л.В. Канторовича (1962) в связи с решением задачи оценки избыточной массы М геологических тел по данным гравиразведки. В качестве результата интерпретации было предложено включение м х 3 м 1, м 2 3, где M 1 и M 2 – неулучшае-мые оценки минимально и максимально возможного значения М . При вычислении M 1 и M 2 использовался метод линейного программирования. К сожалению, эта работа осталась практически незамеченной геофизиками и предложен- ный в ней подход не получил какого-либо заметного развития.

Как альтернативу апостериорной неопределенности, когда при решении практических задач остается неясным, какие свойства «оптимального» решения действительно согласуются с реальным распределением масс в геологической среде, гарантированный подход предлагает тот объем достоверной информации об изучаемом объекте, который фактически содержится в совокупных данных. Такая информация представляет некоторый набор содержательных инвариантов на множестве допустимых решений обратной задачи X 0 . Разыгрывается простая логическая посылка: свойства, присущие всем допустимым решениям из X 0 , присущи и истинному решению X , которое - при условии адекватности модельных представлений – содержится в X 0 , и, следовательно, эти свойства можно рассматривать как достоверную информацию об объекте исследования (в нашем случае – об источниках поля).

Применительно к нелинейной обратной задаче гравиразведки термин «гарантированный подход» был введен в работах П.И. Балка, опубликованных в 80-х гг. прошлого века. Задачу локализации тела S ; предлагалось рассматривать как задачу построения пары t D 1 , D 2 t , где D 1 - минимальная область, содержащая все допустимые решения S * х X 0 (а значит, и S ), а D ₂ – максимальная область, являющаяся фрагментом всех допустимых решений S * (а значит, и фрагментом тела S ). Иначе говоря, для неизвестной области S, занятой аномалиеобразующими массами, предлагалось искать двухстороннюю неу-лучшаемую оценку: D 2 + S + D 1 .

Границы областей D1 и D2 для любого математического метода представляют собой границы возможного решения конкретной обратной задачи. Часть пространства, заключенная между границами областей D 1 и D2 , представляет собой об- ласть неопределенности (ни одну ее точку никаким математическим методом нельзя однозначно идентифицировать на предмет принадлежности носителю S), ее мера t( D 1\ D 2) — есть мера проявления ^ -эквивалентности в конкретной постановке обратной задачи, а величина 1Н t(D2) /1(D1) - мера информативности данных, участвующих в интерпретации [3].

При гарантированном подходе качество результатов интерпретации – это объем извлеченной достоверной информации, предопределяемый совокупной априорной информацией. Это качество (что очень важно) отражает не возможности какого-то математического метода, а реальные возможности геофизического метода в конкретных физико-геологических условиях, что представляет принципиально иной, более высокий уровень понимания проблемы извлечения информации из данных геофизических измерений.

Приведем пример использования гарантированного подхода при интерпрета- ции данных крупномасштабной гравиметрической съемки, выполненной над месторождением платиномедно-никелевых руд (рис. 1). Значительные размеры аномалиеобразующих объектов по простиранию позволяют решать обратную задачу в рамках двумерной постановки. В основу модели среды положены следующие допущения: аномалия поля в основном обусловлена рудоносной интрузией базит-ги-пербазитового состава, ее избыточная плотность (по отношению к вмещающим породам трапповой формации) составляет 0,2 г/см 3 , а суммарная среднеквадратическая невязка поля не превосходит 0,15 мГал.

С помощью монтажного алгоритма решения обратной задачи гравиметрии [1] удалось построить порядка 400 вариантов конфигурационного носителя аномалиеобразующих масс, удовлетворяющих априорным допущениям. Синтез найденных решений позволил установить область (контур 8), с высокой достоверностью принадлежащую источнику аномалии.

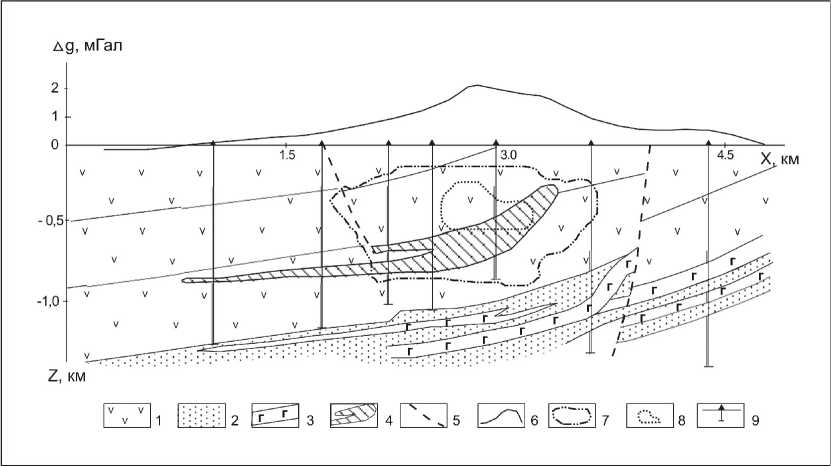
Рис. 1. Результаты интерпретации поля о g месторождения Норильск-1: 1 - породы туфолавовой толщи; 2 – отложения тунгусской серии; 3 – силлы габбро-долеритов; 4 – рудоносная интрузия; 5 – дизъюнктивные нарушения; 6 – локальная составляющая наблюденного поля; 7,8 – результаты интерпретации в предположении адекватности модельных представлений: 7 – область пространства, содержащая источники аномалии, 8 - фрагмент среды, гарантированно принадлежащий источнику поля; 9 – буровые скважины

Смещение ее (относительно фактического положения рудоносной интрузии) в верхнюю часть разреза может свидетельствовать о наличии неучтенного в модели среды ореола уплотнения вмещающих эффузивных пород, что весьма характерно для надинтрузивных зон месторождений Норильского района.

В рамках дальнейших исследований предлагается синтезировать частные решения обратной задачи ж , Ж, ..., & n , опираясь на конечноэлементное представление этих решений, а также на понятие геометрической вероятности. Это понятие фигурирует, в частности, в задаче о бросании точки в ограниченную область G , включающую в себя подобласть g: g + G, в ероятность P попадания точки в эту подобласть определяется как P = mes g/mes G ( mes – мера, здесь размер площади). В данном случае речь пойдет об оценке вероятности P присутствия носителя масс внутри весьма малых фрагментов изучаемого объема геологической среды.

Суть предлагаемого подхода заключается в следующем.

Каждое частное решение представляется в виде совокупности элементарных объемов Ъ , образующих регулярное замощение некоторой части нижнего полупространства. Необходимо пояснить, что регулярным замощением плоскости называется представление этой плоскости некоторым числом правильных замкнутых многоугольников (элементов замощения) f , плотно прилегающих друг к другу по целой стороне. В трехмерном случае элементами замощения могут являться, например, кубы или прямоугольные призмы. Ж 1 , Ж ' , .., Ж представляют собой конфигурационные распределения масс, т.е. произвольные совокупности элементов 3D-нормального регулярного замощения ^ Т U F^ , по каждому из которых распределены массы с постоянной плотностью 4 0 .

По аналогии с детерминистской оценкой достоверности решения ОЗГ строится такая функция ^h ), что ^f ) = 1, если

F ^ + Ж * ; ^h ) = 0, если V ~ X ж * ; при этом получается N вариантов пространственных распределений ее значений (бинарных матриц), отвечающих всем имеющимся решениям ОЗГ. Затем проводится объединение всех этих решений, сводящееся к суммированию N значений ^ F ), характеризующих одни и те же относительно малые области изучаемого объема геологической среды. Результаты такого суммирования представляют собой целочисленную функцию пространственных координат \ = %f ), значения которой располагаются внутри отрезка [0, N ]. Функция X отвечает пересечению допустимых решений ОЗГ, если каждое из них считать конечным множеством, состоящим из элементов F ~ - Ж ^ &₂⁾⁽ U 3 ^U N .

Эту функцию \f ) можно также рассматривать как частоту попадания элемента замощения F во фрагмент моделируемой конфигурации Ж в серии решений ОЗГ, что позволяет естественным образом перейти к вероятностной оценке искомых геометрических параметров. Нормированная функция ^f ) * = ^F )/ N характеризует вероятность P присутствия аномалиеобразующего объекта в элементарном объеме среды F , полученную в результате N равновозможных исходов эксперимента. Очевидно, что в пределах области с нулевыми значениями функции Х = 0 аномалиеобразующие массы будут отсутствовать, а область значений Х = 1 представляет собой фрагмент, гарантированно принадлежащий возмущающему объекту Ж .

Оценка достоверности результатов количественной интерпретации на основе функции \ может существенно повысить вероятность вскрытия искомых аномалиеобразующих объектов в заданных интервалах глубин [ z^н , z^в ] поисковыми и разведочными скважинами, рекомендованными по геофизическим данным.

Локализация геологических объектов по данным гравиразведки и магнито- разведки при неполной информации о физических свойствах горных пород

В известных алгоритмах определения конфигурации геологических тел по гравитационному (магнитному) полю принимается, что плотности (намагниченности) пород, слагающих эти тела, постоянны и заданы априори. В какой-то степени это стало результатом деления обратных задач на линейные и нелинейные, приведшего к двум обособленным направлениям разработки численных методов количественной интерпретации гравитационных (магнитных) аномалий. Вместе с тем по современным представлениям геологические тела – это неоднородные по физическим свойствам мультифрактальные объекты, а постоянная плотность (намагниченность) – это всего лишь условный «эффективный» параметр, замена которым фактического распределения плотности не приводит к заметному изменению поля. Благодаря интегральной природе геопотенциальных полей посылка о существовании «эффективной» плотности (намагниченности) вполне допустима. Но предположение, по которому это значение априори известно, уже не отвечает практике геофизических исследований, особенно если учесть, что значения физических свойств в образцах могут существенно отличаться от физических свойств горной породы в естественном залегании.

В типичных для практики условиях приходится сталкиваться с отсутствием точных сведений о плотности (намагниченности) горных пород, слагающих изучаемые геологические объекты. В этом случае за результат интерпретации целесообразно принимать не точечные оценки параметров аномалиеобразующих объектов, качество которых, строго говоря, случайно, а тот объем достоверной информации об источниках поля, который объективно содержится в исходных данных при условии адекватности модельных представлений. Подобная постановка обратных задач демонстрирует более высокий уровень понимания проблемы извлечения информации из результатов полевых на- блюдений при наличии неопределенности.

Благодаря многочисленным примерам совпадения аномальных эффектов различных однородных тел сложилось мнение, что результаты совместного оценивания физических и геометрических параметров объекта не могут быть удовлетворительными. Но именно смешанные постановки, будучи адекватными реалиям, востребованы на практике, и проблема состоит лишь в том, чтобы обнаружить те типы априорной информации, которые способны уменьшить возросшую неопределенность, довести «размеры» множества всех возможных вариантов интерпретации Q до приемлемых и подобрать подходящий математический аппарат для их реализации. Объективной предпосылкой к успешному решению совмещенной ОЗГ является принцип взаимозаменяемости информации. Предваряя основную постановку задачи, проиллюстрируем его действие на модельном примере, используя 2D-моди-фикацию монтажного метода в варианте регулируемой направленной кристаллизации [1].

Аномалия поля о g обусловлена изолированным выпуклым телом S избыточной плотности ^ t 0,2 г/см3, а среднеквадратическое значение помехи в измерениях поля о g(x,) не превосходит 0,1 мГал (рис. 2, а). На рис. 2,б и 2,в приведены результаты интерпретации при невязке «наблюденного» и модельного полей сЛ 0,2 мГал в терминах пары t D1, D2 t в случае, когда точное значение ^ задано априори (вариант «б»), и в случае, когда известно лишь, что истинное значение ^ лежит в достаточно широком интервале 30,1; 0,э8 г/см3 (вариант «в»). В последнем случае в качестве дополнительной информации выступает предположение, что максимальная вертикальная мощность тела не превышает 2 км (фактически она равна 1,75 км). Легко заметить, что размеры области D1 , гарантированно содержащей аномалиеобразующее тело, в обо- их вариантах оказались сопоставимыми. Область D2 , которая согласно используемому методу заведомо является частью неизвестного тела £, в варианте с нечеткой априорной информацией о плотности лишь на 15% меньше той, что в варианте с известной плотностью. Ясно, что в постановку ОЗГ можно внести еще некоторую дополнительную априорную информацию, которая позволила бы «склонить чашу весов» в пользу последнего варианта.

Создание алгоритмов для решения такого типа задач обеспечит принципиальный прорыв в проблеме наиболее полного извлечения достоверной информации из результатов полевых наблюдений, т. к. построение отдельных приемлемых вариантов интерпретации станет элементом более общей технологии, реализующей концепцию гарантированного подхода и заключающейся в поисках геологически содержательных свойств, присущих всем альтернативным вариантам интерпретации.

Развитие смешанных вероятностно-детерминистских методов решения линейных обратных задач

В 2008–2011 гг. с участием автора статьи был разработан принципиально новый метод решения линейных обратных задач, апробированный для методов

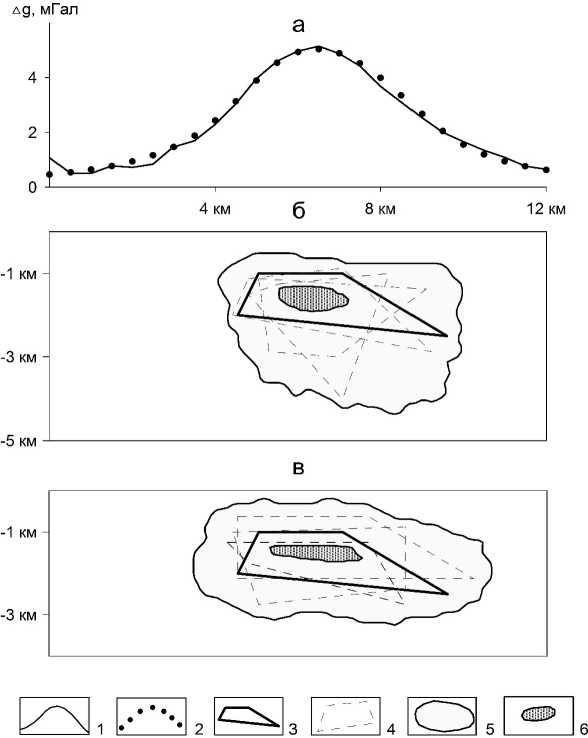
Рис. 2. Результаты интерпретации гравитационной аномалии (а) при точной (б) и интервально заданной (в) плотности ее источника: 1 – «наблюденное» гравитационное поле; 2 – подобранное гравитационное поле для одного из допустимых решений ОЗГ; 3 – источник аномалии; 4 – отдельные допустимые решения ОЗГ; 5 – область D 1 ; 6 – область D 2

гравиразведки, магниторазведки и элек- нировании функционально–аналити-че-троразведки ВЭЗ, основанный на комби-

ского и вероятностно-статистического подходов [6].

Отличительной особенностью метода является способность к подавлению интенсивных знакопеременных помех, закон распределения которых заметно отличается от нормального, а также возможность приближенной оценки точности определения петрофизических параметров изучаемых объектов.

Предположим, что аддитивные помехи ^ i , отягощающие точные значения поля, являются реализациями случайной величины ^ с нулевым медианным значением Me 3 fy 8 1 0 . Если множество D допустимых решений линейной обратной задачи рассматривать как область определения случайного вектора ^- , описывающего возможные значения неизвестных параметров "■■ j , то проблема совмещения двух подходов заключается в том, чтобы по имеющейся информации о свойствах помехи ^fy построить функцию P ( ^ ) плотности вероятностей вектора ^- на множестве D . Фактически определяется вектор оценок - j , минимизирующих математическое ожидание R ( - •) i «( ^ , ~ •) P o C - ) d ~ 1 d ~ 2^ — оши-

D бки Q(-, - *) приближенного решения - * обратной задачи.

Если A – система всех пар (Xs,Xt ) ближайших друг к другу точек измерения поля и K – число таких пар, то необходимо взять множества допустимых решений - , для которых число пар точек (Xt, Xs), в которых разности наблюденного и модельного полей противоположны по знаку, равно r. Вероятности pr подчиняются биномиальному закону, и можно утверждать, что множества 4 r, индексы r которых близки к целому 3 K /28, не могут быть образованы без наиболее точных измерений. Но именно эти множества полу- чают в -ji ^ ?r . —"jd"—d-2---d-m ri i t(® r)•r наибольшие биномиальные «веса» pr , что заставляет график функции u (— *) «прижиматься» к графику функции н(X). Таким образом, предлагаемый метод непосредственно направлен на минимизацию невязки подбираемого и точного поля й( X), тогда как традиционные методы решают эту проблему опосредованно, путем минимизации подобранного и (- *) и наблюденного (зашумленного) поля u~(X), что неэффективно при асимметричных распределениях помех.

Проиллюстрируем возможности этого метода на примере. Оценке подлежит эффективная намагниченность никеленосной интрузии, залегающей под трапповой мульдой на глубине 1500 м (рис. 3). Модули знакопеременных помех распределены по логнормальному закону. Интерпретация выполняется по измерениям поля d Z в 160 точках. Априори известно: 1 1 J 1 , J ₂ I 5, 2 х J 3 х 10 (А/м). Преимущество предлагаемого метода (по результатам 100 вариантов решения обратной задачи) очевидно: средняя суммарная погрешность оценки магнитных свойств по предлагаемому методу составляет 0.52 А/м, а в случае использования минимизации среднеквадратического расхождения полей – 1.25 А/м.

Приведем еще один пример уже для электроразведки методом ВЭЗ. Возьмем геоэлектрический разрез с параметрами * 1 i 1500 Омм, h1 i 10 м; * 2 i 100 Омм, h2 i 50 м; *3 i 900 Омм, h3 i 160 Омм; * 4 i 50 Омм. Кривая ВЭЗ типа НК осложнена равномерно распределенными помехами, амплитуда которых составляет ® 50% от значений "'k на каждом разносе АВ (рис. 4). Средняя (по 50 вариантам решения обратной задачи) точность оценки сопротивлений горизонтов по предложенному методу в 1,5 раза выше, чем при обычной минимизации невязки – 84 против 127 Омм. Прогнозируемая оценка точности результатов интерпретации близка к фактической - R (т (ММР)) t 91

Омм.

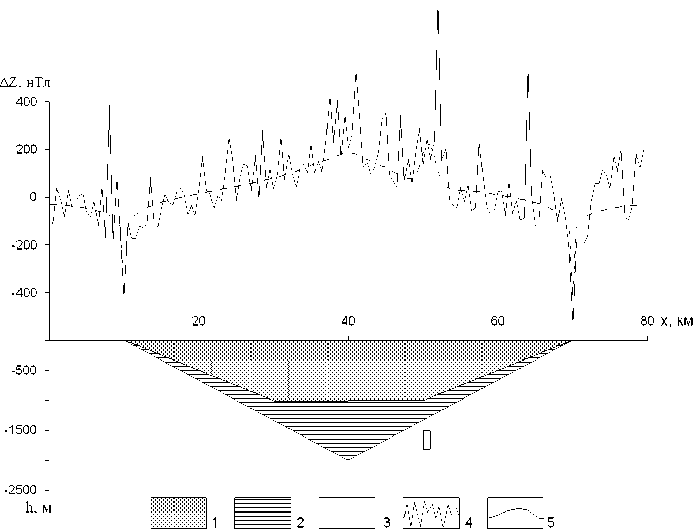
Рис. 3 . Частное решение обратной задачи магниторазведки методом минимизации эмпирического риска: 1 – верхний горизонт эффузивных пород, J 1 = 4 А/м; 2 – нижний горизонт эффузивных пород, J 2 = 2 А/м; 3 - никеленосная интрузия, J 3 = 2 А/м; 4 - магнитное поле aZ без помех; 5 - исходное магнитное поле aZ, осложненное помехами. Подобранные значения намагниченности: J 1 = 3.0 А/м, J 2 = 2.3 Ам, J 3 = 5.5 А/м

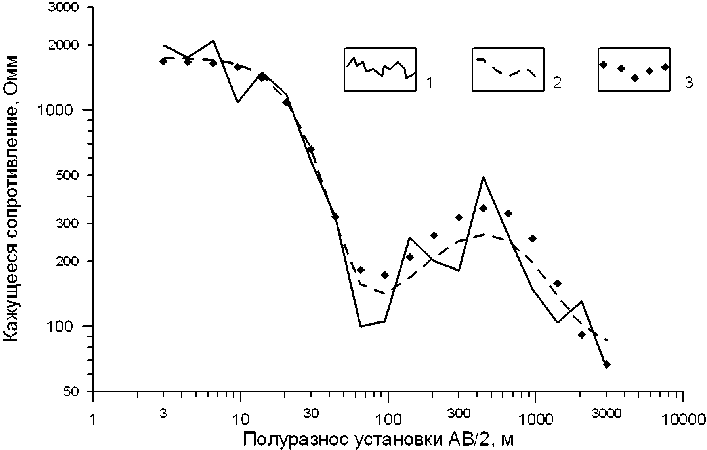
Рис. 4. Частное решение обратной задачи ВЭЗ двумя методами: 1 – исходная кривая ВЭЗ осложненная помехой; модельные кривые ВЭЗ, построенные: 2 – ММН, 3 – ММР. Удельное сопротивление горизонтов, определенное ММН: "'=1750, "2=103, "' з =540, '"=80 Омм; ММР: "'=1692, " 2 =122, " 3 829, ""=50 Омм

Установлена высокая информативность условия равенства нулю медианного значения помех в измерениях, сопоставимая с информативностью детерминистских ограничений на параметры плотностной среды, что лишний раз убеждает в плодотворности идеи комплексирования функционально-аналитического и вероятностно-статистического подходов в алгоритмах решения обратных задач.

В настоящее время данный подход реализован лишь в двухмерном варианте при числе оцениваемых параметров m порядка 4-6. Существенную вычислительную сложность при этом представляет перебор