Совершенствование методов расчета и оценки теплоизоляционных свойств нетканых материалов

Уровень требований к изготовлению и качеству теплоизоляционных материалов вследствие высокой стоимости энергоресурсов, достаточно больших потерь тепла при их транспортировке и экологически вредным производством используемых материалов (например пенополиуретана) сейчас возрос. Особенно важна проблема ухудшения экологии, связанная с нарушением температурновлажностного режима вечной мерзлоты в районах Западной Сибири и Крайнего Севера при прокладке нетеплоизолированных нефте- и газопроводов, что приводит к изменению привычных мест обитания животных и растений. Указанным требованиям отвечают нетканые текстильные материалы, поскольку они имеют достаточную высокую механическую прочность, плотность и пористость, просты и экономичны при производстве.

При математическом моделировании теплофизических характеристик волокнистого материала, предполагаемого к использованию в качестве теплоизолятора, прежде всего необходимо учитывать условия перспективной эксплуатации, которые, в основном, определяются взаимодействием внешней поверхности теплоизоляции с окружающей средой [1; 2].

Анализ исследований, посвященных изучению теплофизических свойств различных дисперсных материалов [3] показывает, что с увеличением плотности возрастает и эффективный коэффициент теплопроводности материала, характеризующий интенсивность молекулярного теплопереноса в структурных элементах, молекулярного и конвективного теплообмена между частицами среды, находя- щейся в порах материала и долю тепла, передаваемого излучением.

Технический текстиль широко используется в различных отраслях народного хозяйства. Ведущее место в указанном классе текстильных изделий занимают нетканые материалы, которые применяются в качестве фильтрующих, геотек-стильных, агротекстильных, звуко- и теплозащитных материалов. Нетканые теплозащитные материалы используются в швейных изделиях, в строительных объектах, в коммунальном хозяйстве, на предприятиях сферы сервиса, для тепловой защиты различных трубопроводов. Для проектирования теплозащитных нетканых материалов и прогнозирования их надежности и работоспособности необходимо знать характеристики их теплозащитных свойств. Одной из основных причин малоэффективного функционирования теплоизоляции является отсутствие методов, которые позволяют определить теплофизические свойства теплоизоляционных материалов с учетом требований, обусловленных условиями эксплуатации в различных областях промышленности и строительства.

Следовательно, разработка методов оценки теплофизических свойств и создание эффективных, экологически чистых, дешевых теплоизоляторов на базе нетканых материалов – весьма своевременная и актуальная задача.

Целью работы является совершенствование методов расчета и оценки свойств нетканых текстильных полотен технического назначения с учетом требований эксплуатации и параметров структуры материалов.

Достижение поставленной цели предполагает: — разработку метода определения эффективного коэффициента теплопроводности λэф теплоизолятора, в зависимости от плотности и пористости материала;

• —    определение рационального волокнистого состава нетканых материалов;

• —    экспериментальную оценку правомерности использования предлагаемой аналитической модели для расчета λ_эф рассматриваемых материалов;

• —    изготовление опытного образца нетканого текстильного материала в соответствии с результатами, полученными аналитическим путем;

• —    разработку и создание экспериментальной установки для определения коэффициента теплопроводности волокнистых материалов на базе современной электронно-вычислительной техники;

• —    разработку методики определения λ_эф волокнистых материалов на новой экспериментальной установке;

• —    экспериментальное определение эффективного коэффициента теплопроводности изготовленного нетканого текстильного материала;

• —    расчет рациональной толщины материала предназначенного для теплоизоляции холодильных установок, горячих трубопроводов и газопроводов;

• —    разработку методики проектирования нетканых текстильных теплоизоляционных материалов с учетом условий эксплуатации.

В процессе проведения теоретических исследований применялись: математические методы анализа функции на экстремум, основные уравнения теории теплообмена в двухфазных средах, табличный редактор Microsoft Excel, программный комплекс «Mathcad PLUS 6.0».

Экспериментальные исследования проводились при помощи: измерителя теплопроводности ИТ-400, разработанной экспериментальной установки с использованием программно-аппаратных средств, лабораторного оборудования.

Проведенный анализ методов математического моделирования и экспериментального определения коэффициента теплопроводности дисперсных материалов, а также требований, предъявляемых к теплоизоляционным материалам в зависимости от условий эксплуатации позволил определить основные направления исследования.

Анализ работ А.В. Лыкова, П.А. Колесникова, Г.М. Кондратьева, А.Ф. Чудновского, В.И. Стельмашенко, Б.Н. Кауфмана, Г.Н. Дуль-нева и др. показал, что в настоящее время не разработаны математические зависимости, которые позволили бы с достаточной для технических расчетов точностью вычислить значение коэффициента теплопроводности дисперсных материалов теоретическим путем, что обусловлено рядом грубых допущений, связанных с заранее заданными формой структурных элементов, градиентом температуры на границе твердой и газовой фаз, размеров пор. Использовать какую-либо из существующих моделей для оценки свойств нетканых полотен крайне затруднительно в связи с хаотическим расположением волокон в материале.

Анализируя методы экспериментального определения коэффициента теплопроводности волокнистых материалов, можно сделать следующие выводы. Приборы, в основу работы которых положен стационарный метод, имеют малую эффективность, обусловленную длительностью проведения опыта, необходимостью в специальных теплоизоляционных устройствах, использованием большого количества термопар и т.д. Более целесообразно использовать приборы, основанные на методе регулярного теплового режима, что основывается на относительной простоте и точности проведения эксперимента, независимости результатов опытов от начального теплового состояния образца.

Разработка метода анализа и расчета эффективного коэффициента теплопроводности нетканого теплоизоляционного материала.

Необходимость разработки нового метода обусловлена тем, что ни один из существующих методов не учитывает условий перспективной эксплуатации теплоизоляционного материала, а также хаотическое расположение волокон в иглопробивных нетканых полотнах.

При разработке нового метода, позволяющего провести расчет эффективного коэффициента теплопроводности, целесообразно представить рассматриваемый нетканый материал как вязкоупругую сплошную среду, имеющую капиллярнопористое строение и волокнистую структуру.

Положенная в основу аналитических исследований степенная зависимость эффективного коэффициента теплопроводности материала Хэф от отношения плотностей материала pv и волокон Y базируется на результатах анализа научных работ Б.А. Бузова, П.А. Колесникова, В.И. Стельма-шенко, А.П. Жихарева, К. Торкара, А.С. Лялико-ва, В.З. Богомолова и других ученых:

Х эф = L х (p_v / Y) m ,                           (1)

Для вычисления значений Х _{э ф}, p_V/y, L и m использован метод исследования на экстремум заданной функции при наличии дополнительных условий:

• 0, при P 1 <  ⁽ p V / Y) < Р 2

• ^F( Y) = ^[(P v / Y ) — Р 2 ^] при ⁽P v / Y) ^ P 2   >

[Pi — (Pv / Y)] при (Pv / Y) < Pi где p1 , p2 - величины отношения (pv / y) соответственно при минимальном Х1 и максимальном Х2 значениях эффективного коэффициента теплопроводности.

Искомым является вариант, при котором в интервале p₁< (p_v /у) < p₂ минимумы F(Y) и исследуемой функции L х Y ^m = L х е ^{[m x ln (Y)]} совпадают:

dM1

----- = 2 х J [ L х Ym - F (Y) ] Y m dY = 0

dL0

dM1

----— = 2 х J [L х Ym - F (Y)] х L х Ym х In (Y )d Y=0 dm0

где M i ( L, m) = J [ L х Y ^m - F(Y) ]² dY.

После преобразований приведенных уравнений получены зависимости для определения параметров модели: показателя нелинейности функции m в виде

[1/(m +1)]х {p₂^{( m +} ° х [1- (m + 1)х In (p₂)] -- P₂ - P₁^{(m +1} ) х [( m + 1)х In (p₁) - 1]} +

+ [1/(m +1)²]х{p₁^{(m + 2} ) х [(m +2)х In (p₁) - 1] -- p₂^{(m + 2)} х [1 - (m + 2)х In (p₂)] + 1} —

• - {1/[(2m +1)х(m + 1)х(m +2)]}х [p₁⁽ m ^{+ 2)}+ m х х (1 - p₂) + (1- 2хр 2 ) + p₂^{(m + 2} ) = 0;

• — коэффициента пропорциональности L:

L = [(2хm + 1) / (m +1)х(m +2)] х [p₁^{(m + 2} ) + + шх(1 - p₂) + (1 - 2хр 2 ) + p₂^{(m + 2} ) ].

В качестве замыкающих используется выражение (1), записанное для Х1 и Х2:

ln(X1) = ln(L) + m х In (p1); ln(X2) = ln(L) + m х х ln (p2).

Величины Х₁ и X₂ определяются исходя из условий эксплуатации материала. Численные значения Х_эф зависят от среды, заполняющей поры: воздух, вода, лед. Для каждого варианта вычислены L, ш и получены формулы для определения Х_эф:

I вариант — воздух: Х_эф = 0,982х(p_V / y)^1,119;

II вариант — вода: Х_эф = 0,502х(p_V / y)⁰ , ⁰¹⁰³;

III вариант — лед: Х_эф = 0,248х(p_V/ y)^{— о} , ²⁹⁰.

В случае, если часть объема материала занимает вода, а другую часть лед, для расчета Х_эф в зависимости от X_v и (p_v / y) было получено следующее выражение, описывающее взаимосвязь Х_эф, X_v и ⁽ P v / Y)

Хэф = Х31 х Х2 / {\1 х [(Уi — У0) / (У 1 — У0)] + Х2 х х [ 1 — (Уi — У0) / (У1 — Уо)]} где (y1 — y0) — толщина материала; yi — граница раздела «лед – вода»;

Х₅₁, Х _б2 — коэффициенты теплопроводности твердой (лед) и жидкой фаз (вода).

Кроме соотношения p_v / y, определение рациональных Х_эф следует проводить на основании общих и специальных требований к структурным элементам теплоизолятора, к которым относятся устойчивость к воздействию: микроорганизмов, минеральных кислот и щелочей, некоторых органических соединений, светопогоды, температуры, влаги и т.д. С учетом изложенных требований целесообразно применять химические волокна, из которых наименее гигроскопичны полиэфирные, полипропиленовые, полиамидные и стеклянные.

Для простоты и удобства определения волокнистого состава при изготовлении качественного теплоизоляционного нетканого материала по заданным значениям Хэф и pv / y, на основании про- веденных расчетов разработан графический метод. Для пользования такими номограммами достаточно знать или задать какую-либо из характеристик: эффективный коэффициент теплопроводности материала λэф или коэффициент теплопроводности волокон λv или соотношение плотностей материала и структурных элементов ρV / γ. Пример такой номограммы представлен на рис. 1.

проведение опыта, оценкой термоЭДС по стрелочному прибору и ручным регулированием режима измерений. В связи с этим разработана измерительная установка на базе компьютера IBM, позволяющая автоматизировать процесс проведения опыта, фиксировать значения термоЭДС посредством программно-аппаратных средств и сократить время эксперимента.

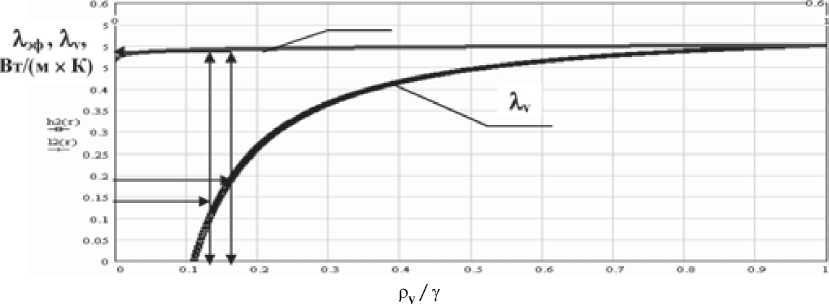
рис. 1 . Определение рациональных значений эффективного коэффициента теплопроводности λ _эф в зависимости от λ _v и ρ_v/ γ . Вариант II

Экспериментальные исследования коэффициента теплопроводности нетканых текстильных материалов технического назначения.

С целью оценки правомерности предложенного аналитического метода расчета λэф = f(ρV/γ) были проведены измерения λ на приборе ИТ-λ-400 в соответствии с методикой для пользователей. В процессе исследований использовались образцы холста стекловолокнистого ХСБТ-90 и полотна нитепрошивного стекловолокнистого НПГ-750. В результате эксперимента установлено, что погрешность расчетов λэф по отношению к опытным данным не превышает 7,38% при температурах –30 …–20 °С. В области положительных температур 0 ÷ 190 °С погрешность составляет не более 5%. Таким образом, можно сделать вывод о правомерности использования предложенной методики для расчета λэф.

На основании проведенных исследований определены требуемые параметры теплоизоляционного нетканого материала, в соответствии с которыми разработан и изготовлен опытный образец из полиэфирных волокон, имеющий: толщину 12 мм; поверхностную плотность – 500 ± 15 г/м2; объемную плотность – 46 кг / м3.

Использование ИТ–λ–400 имеет недостатки, связанные с большими затратами времени на

В основу создания такой установки положен метод регулярного теплового режима. Управление экспериментальной установкой осуществлялось через коммуникационный порт, режимы работы которого заданы специально написанным драйвером. В результате этого обеспечивается: включение и выключение нагревательного элемента; измерение температуры в нагревательной камере; численное и графическое отражение результатов измерений во времени.

Методика проведения эксперимента заключается в следующем. Образец исследуемого материала помещался между пластинами, одна из которых контактировала с нагревательным элементом (сердечником), а другая – с буферной жидкостью, находящейся в измерительной камере. Эта жидкость необходима для уменьшения температурного градиента и увеличения инерционности хромель-копелевых термопар, расположенных на поверхностях пластин. Скорость и диапазон изменения температуры определялись опытным путем. После достижения заданного перепада температур на образце, электронагреватель отключался, и дальнейший подвод тепла происходил по инерции. По окончании инерционного периода образец охлаждался в диапазоне заданных температур, отслеживаемых аналого-цифровым преобразователем (АЦП) и ЭВМ. Термопары подключались на вход АЦП таким образом, чтобы ЭВМ регистрировала термоЭДС, соответствующую разности температур ∆t на обеих пластинах. В экспериментальной установке применялся АЦП марки ADC-12-60 с гальванической изоляцией каналов измерения, позволяющий преобразовывать в 12-разрядный двоичный код аналоговые сигналы, подаваемые на вход устройства. Для подключения АЦП к каналу ЭВМ были разработаны интерфейсы на базе интерфейса параллельного обмена МИТ (модуля интерфейсного типового), выполненного в виде двух печатных плат. Значения термоЭДС в характерных точках и времени проведения эксперимента были получены при тарировочных испытаниях установки. В качестве эталонного образца использовался поролон толщиной 10 мм и λ = 0,03555 Вт/(м × К).

С целью проверки точности измерений λ на новой экспериментальной установке, первоначально подвергались испытаниям образцы материалов ХСБТ–90 и НПГ–750, коэффициенты

Измерения λ нетканых материалов

теплопроводности которых были определены при помощи ИТ–λ–400. Затем проводились измерения λ других нетканых материалов (табл. 1). Результаты эксперимента представлены на рис. 2.

В результате эксперимента установлено, что для выработки теплоизоляционных нетканых полотен целесообразно применять полиэфирные волокна, так как их теплопроводность меньше полипропиленовых. Кроме того, установлено, что структура (волокна или элементарные нити из одного полимера) не оказывает существенного влияние на теплофизические свойства материала.

Анализ результатов исследований коэффициента теплопроводности разработанного нетканого материала (образец № 8) показывает, что он может быть использован в качестве теплоизолятора. Погрешность значений коэффициента теплопроводности изготовленного материала, определенных опытным путем по отношению к рекомендуемым расчетным величинам λэф не превышает 3,46%.

Таблица 1

Образец			№ 1	№ 2	№ 3	№ 4	№ 5	№ 6	№ 7	№ 8
Сырьевой состав			о m EZ	1 11	1 11	Ct 1 1	EZ EZ		EZ	II
ρ V, кг/м3	51.4	37	173.1	121.9	84.2	85.81	77.71	82.8	55.6	46

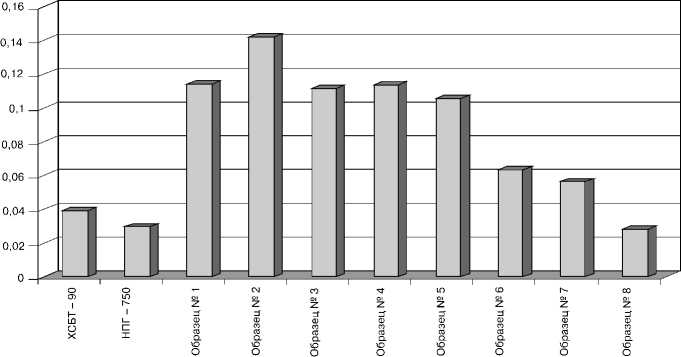
рис. 2 . Результаты измерений коэффициента теплопроводности материалов

Практическое применение результатов исследований для расчета рациональной толщины теплоизоляционного материала в зависимости от условий эксплуатации.

Толщина теплоизоляции холодильных установок определяется исходя из анализа теплообмена между холодильной камерой и окружающей средой:

S i = X i X [(1 / {1 / [(1 / a . ) + (S i / X i ) + (1 / « 2 ) ]})— — ⁽¹ / ^a 1 ) — ⁽¹ / ^a₂ ^)] , где a 1 и a₂ — коэффициенты теплоотдачи от воздуха к стенке с холодной стороны и от стенки к воздуху с теплой стороны;

S . , X i — толщина и эффективный коэффициент теплопроводности теплоизоляции.

Расчет S i проводился по общепринятым величинам коэффициентов теплопередачи и теплоотдачи, а также температурам воздуха в помещении и холодильной камере, рекомендуемым НИИ Гипрохолод, СНиП II-А.7-71 «Строительная теплотехника. Нормы проектирования», СНиП II-А.6– 72 «Строительная климатология и геофизика». Результаты расчета приведены в табл. 2.

Таблица 2

Температура в камере, 0С	Толщина изоляционного материала в м при температуре окружающей среды, °С
	12	20
–0	0,055	0,063
–5	0,063	0,075
–10	0,075	0,092

Расчет теплоизоляции горячих трубопроводов производятся исходя из норм теплопотерь, установленных в зависимости от диаметра трубопровода и величины полного температурного напора между теплоносителем и окружающей средой. Полное термическое сопротивление трубопровода R определяется:

R = 1 / (a x d 2 ) + (1/ Х_ст) x ln(d 1 / d 2 ) + [1 / (2 x x п x X i )] x ln(d i / d 1 ) + 1/[ nxa₂xd1], где d_i, d₁, d₂ — диаметр теплоизоляции; внешний и внутренний диаметры трубы;

• a, a₂ = 8,1 + 0,045 х (1 т — 1_н) — коэффициенты теплоотдачи от теплоносителя к внутренней стенке трубы и от трубы в среду с температурой t_в.

Анализ величин термических сопротивлений показывает, что величина R_e = 1/(axd₂) минимум в 10^20 раз меньше R i = [1/(2xnxX i )] х ln(d i /d₁). Также весьма незначительно R_o = (1/Х_ст) х ln(d 1 / d₂). В этом случае определение R упрощается:

R = [1 / (2 х п х X i )] х ln(d i / d 1 ) + 1 / [пх a₂ х d 1 ].

Отсюда получены уравнения для вычисления диаметра и толщины теплоизоляции:

d i = d , x e^A и S i = (d i — d 1 ) / 2, где: А = (2xnxX i )x[R — (1/nxa2xd1)].

Расчет толщины теплоизоляции проводился при значениях: 1_т = 100 °С; X i = X_эф = (0,025^0,028) Вт/(мхК); 1 н = 0^5; 10; 15; 20‘°С. '

Сравнение полученных результатов и данных по наиболее экономичной толщине теплоизоляции показывает, что расчетные значения более рациональны с точки зрения стоимости тепла и времени эксплуатации трубопровода.

Критерием при определении рациональной толщины теплоизоляционного пакета подземного газопровода является минимальный ореол (зона) оттаивания вечномерзлых грунтов вокруг трубопровода.

При расчете теплопотерь с одного погонного метра трубопровода, находящегося на глубине h, применяется закон Фурье, который для рассматриваемой задачи с учетом незначительности Rв и Rп имеет вид:

q = ^{2 х} п ^{х (t} _T ^— t_r) / ⁽ 1 / ^X i ) ^х ln ⁽ r i / r₁ ⁾ + (1 / X) х In [2 х ( h + r i ) / r i )]

где tт, tг – температура теплоносителя и грунта соответственно;

• X i , X_r, X_ct - коэффициенты теплопроводности теплоизоляции, грунта и трубы;

ri, r1, r2 – радиус теплоизоляции, внешний и внутренний радиусы трубопровода.

Радиус ореола оттаивания вокруг трубы r0 и смещение вниз центра ореола оттаивания по отношению к центру трубопровода С вычисляется:

r₀ = 0,5 х (h 1 — h 2 ); C = 0,5 х (h 1 + h 2 ) — (h + r i ). где h 1 = {{r i х {[( h + r i )/ r i ]² - 1} °.5 x(e^d + 1)}}/(e^d — 1) — глубина оттаивания грунта;

h₂ = {{r i х {[(h + r i ) /r i ]² - 1}^0A х (e^d — 1)}} / (e^d + 1) — мощность мерзлого грунта;

d = 2xnxX_rrxb_ix{ln [(h + r . )/r] + [(h/r i )² — 1] °. ⁵/2хпхX_rт}/(1 + ^b); b t =^—L^{х tr/(X}„^х V;

X™, X_гт — коэффициент теплопроводности грунта в мерзлом и талом с остоянии.

В результате расчетов установлена минимальная толщина слоя Smin = 0,01 м (радиус трубы 0,2645 м) и максимальная Smax = 0,1205 м (радиус трубы 0,710 м).

С целью унификации теплоизолятора при его производстве следует принять минимальную толщину материала 0,012 м и 0,017 м, а достижение требуемой толщины теплоизоляционного пакета осуществлять путем наматывания на трубопровод необходимого числа витков.

На основании проведенных исследований разработана методика проектирования нетканых материалов с учетом условий эксплуатации.

исcледование эксплуатационных показателей качества материалов...

ВЫВОДЫ

• 1.    Разработан метод расчета эффективного коэффициента теплопроводности λ_эф в зависимости от отношения плотностей материала и волокон. Погрешность расчетных значений по отношению к экспериментальным данным в диапазоне температур (-30) ÷200 °С не превышает 5%.

• 2.    Для простоты и удобства определения волокнистого состава при изготовлении качественного теплоизоляционного нетканого материала по заданным значениям λ_эф и ρ_V / γ, разработан графический способ определения волокнистого состава и требуемых параметров нетканого теплоизоляционного материала.

• 3.    Разработана, изготовлена и прошла лабораторные испытания установка для измерения коэффициента теплопроводности волокнистых материалов, а также разработана методика определения λ_эф на новой экспериментальной установке.

• 4.    Разработана методика проектирования нетканых материалов с учетом условий эксплуатации, предназначенная для расчета параметров теплоизоляции газопроводов, прокладываемых в районах вечной мерзлоты.