Совершенствование профессиональных компетенций учителей математики по использованию задач на готовых чертежах

Введение. Вопросы, связанные с совершенствованием компетентностей, направленными на применение задач на готовых чертежах в условиях развития информационнокоммуникационных технологий (ИКТ), являются достаточно важными для современного учителя математики.

Таблица 1

Некоторые проблемы и надежды на их решение, возникающие при изучении геометрии в школе

Возможности совершенствования изучения геометрии	Проблемы освоения геометрии
Развитие ИКТ	Затруднения у многих школьников с получением качественных рисунков к задачам
	Трудности с обоснованием решения задач
Интерес школьников к освоению современных инструментов построения и анализа рисунков
	Достаточно низкие результаты в геометрической части ЕГЭ(ОГЭ) и олимпиад

Таблица 2

Некоторые результаты регионального этапа ВсОШ по математике в текущем году

Класс	Количество учащихся	Первый день		Второй день
		номер задачи	количество решений	номер задачи	количество решений
8	30	8.3	4	8.9	1
9	23	9.5	0	9.8	1
10	27	10.5	0	10.8	0
11	24	11.4	0	11.8	2,5

В частности, это обосновывается наличием следующих противоречий в овладении современными школьниками учебного геометрического материала (табл. 1).

Отмечаются достаточно низкие результаты в геометрической части ЕГЭ (ОГЭ) и олимпиад весьма заметных как на федеральном, так и на региональном уровнях. Причем это касается, как участия школьников Липецкой области в перечневых (вузовских) олимпиадах, так и наблюдается на различных этапах Всероссийской олимпиады школьников (ВсОШ) по математике. Например, в текущем году, представитель региона на финальном этапе ВсОШ не сумел набрать баллов по геометрической части заданий, не было у него баллов по геометрии и на региональном этапе. С другой стороны, набранные 8 баллов в геометрической части финального этапа прошлого года, позволили представителю региона стать призером олимпиады.

Некоторая статистика по решению геометрических задач на региональных этапах ВсОШ и олимпиады Эйлера в текущем году приведена в таблице 2.

Аналогичные результаты просматриваются и при анализе итогов ЕГЭ (ОГЭ).

Данное исследование, в частности, направленно на то, чтобы чаша весов на рисунке 1 наклонилась в другую сторону.

Одной из существенных причин выявленных проблем является потребность в совершенствовании уровня профессиональной подготовки, как предметной, так и методической, учителя математики и педагога дополнительного образования (ДО).

Цель исследования заключается в обосновании совершенствования содержания повышения уровня профессиональной компетентности учителя математики в части применения задач на готовых чертежах с учетом современного развития информационно-коммуникационных технологий (ИКТ).

Обзор литературы. В научно-методической литературе структура и содержание курсов повышения квалификации (ПК) различной направленности обсуждается достаточно широко. Например, А. В. Грошева анализирует технологические аспекты разработки дополнительных профессиональных программ повышения квалификации педагогических работников [1].

Многие авторы выделяют проблемы непосредственно геометрического образования. Так, Н. А. Бородулина отмечает «… умение решать геометрические задачи является у современного школьника наименее развитым. Об этом свидетельствуют результаты ОГЭ в Калининградской области» [2, с. 63].

Ряд исследователей активно обсуждает целесообразность применения устных упражнений [3], в частности на таких этапах урока математики, как этапы мотивации, целеполагания и организации деятельности, актуализации опорных знаний [4, с. 271], анализируют формы организации устного счета [5, с. 115–116], особенности использования устных заданий развивающего характера c помощью средств ИКТ [6, с. 347–348]. Е. Р. Данилкова проводит анализ геометрических устных упражнений как со словесным условием, так и заданий на готовых чертежах, в том числе исследует некоторые возможности применения сервиса geogebra.org [7, с. 149]. Ю. О. Слета выделяет типы заданий, направленных на обучение анализировать условие задачи и соответственно строить чертеж: «задачи на выделение объекта и записи его названия; задачи на комбинацию фигур; задачи на нетипичное расположение фигуры; задачи с недостающими данными; задачи без сформулированного вопроса» [8, с. 86]. А. Б. Гимаева обосновывает необходимость использования задач на готовых чертежах при подготовке к ОГЭ [9].

Сфера применения заданий на готовых чертежах не ограничивается применением их на классических уроках, они предлагаются во внеурочной деятельности [10, с. 146–147], при дистанционной работе [11, с 59]. Ряд педагогов исследуют возможности различных программных систем. Так, К. К. Ляпина отмечает, что «среда „1С: Математический конструктор“ рассчитана на создание интерактивных чертежей по математике, включающих и конструирование, и моделирование, а также динамическое варьирование с возможностью экспериментировать» [12, с. 61].

Вопросы, связанные с формированием цифровых компетенций в процессе повышения квалификации учителя математики, рассматриваются достаточно часто. Например, анализируются особенности математического модели- рования с применением цифровых технологий [13, с. 48].

Практическая составляющая по созданию учебных моделей с использованием программы динамической геометрии GeoGebra на КПК учителей математики может формироваться при разработке соответствующих дидактических средств [14, с. 51–52]. Все перечисленное подтверждает разумность разработки краткосрочных курсов по развитию компетенции учителей математики и педагогов ДО в контексте использования задач на готовых чертежах с применением ИКТ.

Методология (материалы и методы). Методологическую основу исследования составляют теоретические методы: изучение и анализ научно-методической литературы, сравнительно-сопоставительный анализ существующих точек зрения, обобщение опыта повышения компетентности педагогов в направлении применения задач на готовых чертежах. Для уточнения отдельных аспектов обучения школьников геометрии, в частности планиметрии, в условиях развития ИКТ и построения примерной схемы организации работы с заданиями на готовых чертежах использовались эмпирические методы (наблюдение, анкетирование, анализ результатов исследования, опытноэкспериментальная работа).

Результаты и их описание. В рамках исследования проводились систематизация и планирование определенных действий с акцентом на повышение квалификации учителей с целью совершенствования профессиональных компетенций, направленных на применение задач на готовых чертежах в условиях развития ИКТ. Предлагаемые шаги, на наш взгляд, должны повысить профессиональную подготовку учителя математики и педагога дополнительного образования. А работа педагогов, в свою очередь, будет повышать геометрическую подготовку учащихся. Первоначально выделим некоторые положительные аспекты влияние развитие ИКТ на расширение возможностей применения в школе заданий на готовых чертежах:

• —    улучшение качества применяемых рисунков (geogebra.org, «1С: математический конструктор» и т. д.);

• —    уменьшение времени на предварительную подготовку чертежей;

• —    оперативное дополнение и/или модификации заранее подготовленных изображений (особенно при использовании интерактивных экранов);

• —    одновременное предъявление на экране (мониторе) нескольких задач (серии задач);

• —    повышения уровня сложности рассматриваемых в устном режиме задач, благодаря возможности разбиения задачи на подзадачи, с поочередным предъявлением рисунков;

• —    расширение потенциала использования игрофикации (геймификации);

• —    возможность применения интерактивной визуализации, например, при изучении геометрических преобразований, а также при обучении решению соответствующих задач;

• —    оперативное сочетание практической деятельности с повторением теоретического материала;

• —    повышения уровня межпредметных компетенций школьников (в случае привлечения учащихся к подготовке рисунков, разработке игровых компьютерных приложений с геометрическим материалом, квестов, квизов и т. д.).

На основе проведенного анализа выявлена целесообразность проведения курсов ПК, позволяющих помочь педагогам использовать преимущества современного уровня развития ИКТ для уменьшения проблем в освоении школьниками геометрии, планиметрии в частности.

Приведем примерную структуру краткосрочных курсов повышения квалификации учителей с целью совершенствования профессиональных компетенций, направленных на применение задач на готовых чертежах с пользованием современных ИКТ (табл. 3). В модуле «Обзор средств построения планиметрических чертежей (рисунков)» анализируются такие инструменты, как geogebra.org, «1С: математический конструктор» и т. д. В разделе «Изучение возможностей сервиса geogebra» предлагается рассмотреть следующие структурные элементы:

• —    анализ возможностей построения некоторых планиметрических фигур;

• —    примеры построения фигур, удовлетворяющих определенным свойства: фигуры, имеющие фиксированные размеры или другие метрики, правильные многоугольники, дуги по отдельным точкам и т. д.;

  Примерная обобщенная структура краткосрочных КПК

  
  

  Таблица 3

  Обзор средств построения планиметрических чертежей (рисунков)
  Изучение возможностей сервиса geogebra	Формирование набора задач/теорем
  Формирование банка заданий
  Методические особенности применения подготовленных заданий на уроках геометрии	Методические особенности применения подготовленных заданий в системе дополнительного образования

  
  

• —    формирование элементов, связанных с ранее построенными: точки пересечения, перпендикулярные прямые, биссектрисы, касательные и т. д.;

• —    оформление сопроводительных надписей, в том числе, в формате Latex;

• —    построение фигур с использованием алгебраического инструментария, например построение фигуры по имеющемуся ее уравнению (неравенству);

• —    применение геометрических преобразований;

• —    получение метрических значений: длин отрезков, площадей фигур, угла наклона;

• —    размещение на рисунке элементов управления: кнопок, ползунков, окон ввода, флажков и т. д.

Модуль «Формирование банка заданий» предусматривает сетевую работы для получения большего количества иллюстраций для задач разного уровня сложности.

В предлагаемых курсах повышения квалификации существенный акцент делается на выполнение практических заданий.

Практические задания могут содержать примеры построения рисунков к заданиям ЕГЭ, ОГЭ, задачам различных олимпиад. Также предлагается формирование банка заданий для геометрического брейн-ринга. Описание предлагаемого нами командного соревнования «Геометрический брейн-ринг» приведено ниже.

Приведем сокращенные примеры предлагаемых практических заданий.

Условие задачи (отборочный этап инженерной олимпиады школьников центра России по математике, 2023/24 уч. г.): «На окружности ω, вписанной в равносторонний треугольник ABC, взята такая точка M, что угол AMC равен 120º. Докажите, что окружность ω делит отрезок BM пополам».

Для данной задачи выполните следующие действия:

• —    постройте рисунок по исходным данным задачи;

• —    получите второй рисунок, содержащий дополнительные построения, облегчающие получение решения задачи;

— определите, средствами geogebra, длины частей отрезка BM , на которые он делится окружностью ω .

Три полученных варианта приведены на рисунке 1.

Еще один пример практического задания. Составить три варианта заданий разного уровня сложности, иллюстрирующих одинаковый теоретический материал, для геометрического брейн-ринга. Результат выполненной работы приведен на рисунке 2.

Слушателям предлагается достаточно стандартная тематика заданий данного вида (предлагаются, как темы базового курса геометрии, так и темы для профильных классов и групп олимпиадной подготовки).

Развитие ИКТ позволяет достаточно быстро получать не только качественные чертежи (рисунки), но и более сложные, мультимедийные элементы. Таким образом, решение задач на готовых чертежах в современных условиях может трансформироваться в решение задач с использованием готовых видеофрагментов, сценариев, проектов.

В рамках курсов повышения квалификации рассматриваются и методические вопросы, связанные с организацией работы с заданиями на готовых чертежах.

Нами предлагается следующая примерная схема сочетания современных возможностей ИКТ и решения задач на готовых чертежах или с применением готовых видеофрагментов, сценариев, проектов:

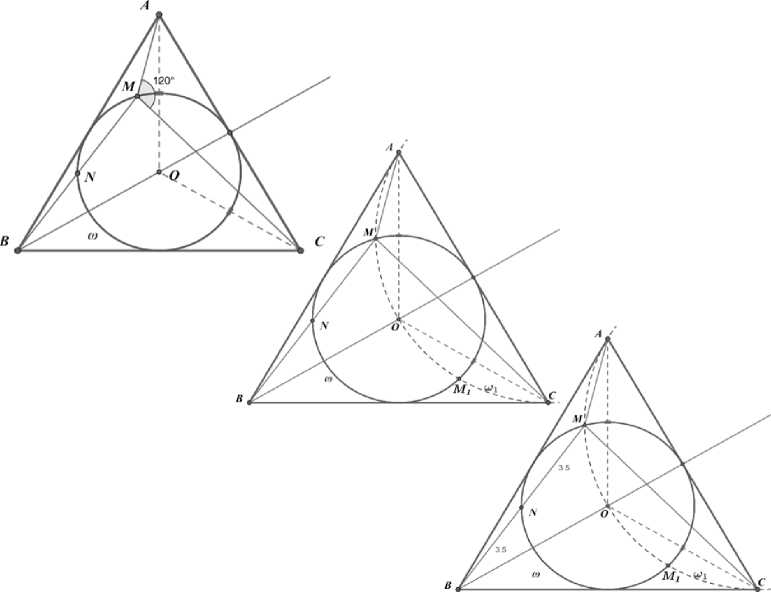
Рис. 1. Пример результата выполнения практического задания

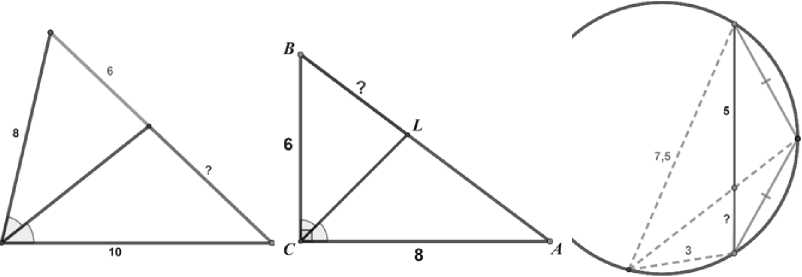
Рис. 2. Пример результата выполнения практического задания второго вида

• —    выбор задачи (задач, теорем);

• —    формирование сценария (примерной схемы рисунка, серии рисунков и т. д.);

• —    разработка рисунка (рисунков);

• —    реализация плана (сценария) решения задачи;

• —    подведение итогов, формулировка выводов.

Классификация организации работы с геометрическими задачами в школе по уровням использования рисунков (чертежей):

• —    построение рисунков выполняется самостоятельно с использованием только чертежных принадлежностей, разрешенных форматом ЕГЭ/ОГЭ;

• —    школьники выполняют построение рисунков самостоятельно с использованием всех чертежных принадлежностей;

• —    самостоятельное построение рисунков с помощью сервиса geogebra.org или аналогичных средств;

• —    учитель предлагает готовый чертеж только на основе данных из условия задачи;

• —    предлагается готовый рисунок/рисунки на основе данных из условия задачи и данных, достаточно очевидно вытекающих из него;

• —    задачу иллюстрирует готовый чертеж, отражающий информацию из условия задачи, дополнительно он содержит подсказки для получения решения;

• —    преподаватель поочередно предъявляет серию готовых рисунков, которые подводят школьника к получению решения.

Современные ИКТ позволяют в большей мере совмещать серьезное и несерьезное. В частности, отработку достаточно важных для учащихся знаний, можно объединять с геймификацией (игрофикацией) учебного процесса.

Например, нами предлагается математическое соревнование с игровыми элементами «Геометрический брейн-ринг». Соревнование состоит из некоторого количества боев, проходящих по достаточно известным правилам брейн-ринга, в каждом поединке может участвовать от двух до четырех команд. Для проведения мероприятия требуется определенное оборудование (кнопки для сигнализации о решении задач, компьютер для фиксации времени и перехода между вопросами, проектор (интерактивная или сенсорная доски), а также необходимо подключение к интернету для фиксации результатов поединков и ведения таблицы этих результатов.

Бой состоит из нескольких вопросов (обычно 5–7) предполагающих решение планиметрических задач. В отличие от обычного варианта брейн-ринга, в предлагаемом нами варианте, ведущий не читает вопрос, задание отображается на экране в виде чертежа. Чертеж содержит информацию об известных в задаче данных, вопросительный знак соответствует искомой величине. После этого команде дается 30–60 секунд на размышление. Объем времени на раздумья зависит от цели мероприятия, сложности задач, договоренности между участниками. Команда, готовая ответить на вопрос, нажимает на кнопку. Команда, нажавшая кнопку первой, получает право ответа. Капитан называет игрока, который будет отвечать, после этого игрок дает ответ и пояснение, если вопрос требует до- полнительных комментариев. При этом отвечающий игрок не имеет права совещаться с командой и затягивать время, в противном случае ответ будет признан неверным. Если команда ответила неправильно, то 30 секунд (при 30 секундном формате) на размышление получает команда соперника. В случае количества команд большего, чем две, время на раздумья в дальнейшем уменьшается. Нажимать на кнопку можно в любой момент после объявления номера вопроса до истечения времени на размышление (игра без фальстартов).

Большинство задач, упоминаемых в данной статье, а также другие несложные планиметрические задачи на готовых чертежах вполне можно применять в соревновании «Геометрический брейн-ринг». Требуется следить за соответствием уровня подготовки учащихся степени сложности задач. Задания на рисунке 3 направлены на отработку важного навыка поиска вписанного четырехугольника, если напрямую в задаче он не упоминается. Предлагаемые задания дают возможность примерно за 15 минут устного счета повторить или закрепить основные признаки вписанного четырехугольника. Учащиеся могут выбрать произвольный порядок выполнения заданий.

Обсуждение. По итогам проведения курсов повышения квалификации было проведено анкетирование слушателей с целью определения примерного количественного объема заданий на готовых рисунках в общем количестве планиметрических задач, разбираемых на занятиях.

Слушателям были предложены шесть вопросов о роли геометрии в развитии математической культуры школьника и использовании задач на готовых чертежах.

В рамках исследования нас интересовали ответы на вопрос: «Выберите один вариант ответа, соответствующий вашему мнению о количественном объеме заданий на готовых чертежах в общем количестве планиметрических задач, разбираемых на уроках (на занятиях в системе дополнительного образования)».

Предлагаемые варианты ответов: свыше 50% (проголосовало 9,5% анкетируемых), от 30% до 50% (21,4%), от 10% до 30% (57,1%), менее 10% (11,9%), нецелесообразно использовать (0%).

Найдите вписанный четырехугольник

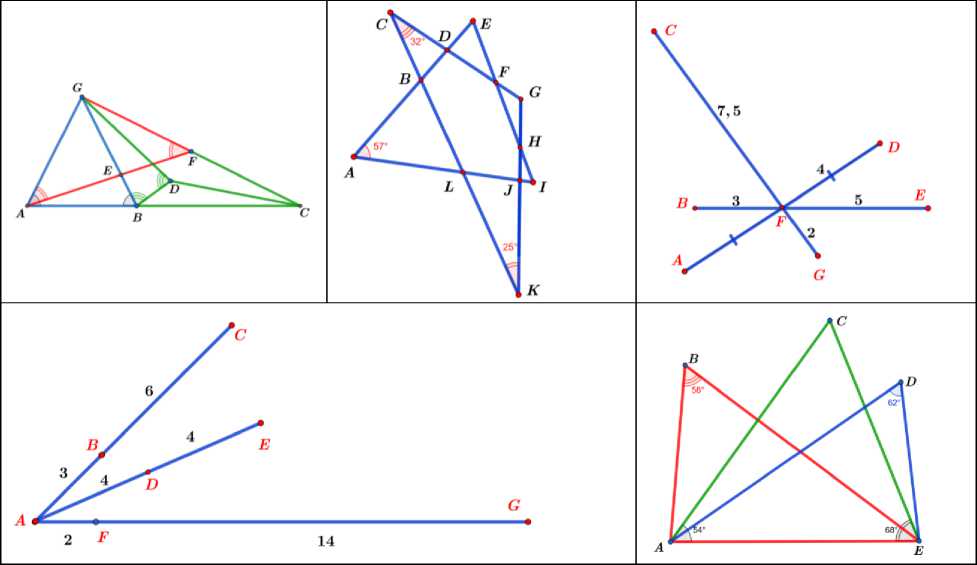
Рис. 3. Пример заданий на готовых чертежах с произвольным выбором порядка их выполнения

Также слушателям предлагалось в произвольной форме выразить свое мнение о провидимой курсовой подготовке и в целом о целесообразности применения средств ИКТ при обучении школьников решению планиметрических задач. В анкетировании приняло участие 42 педагога, больше половины из которых принимали участие в работе курсов ПК.

Многие учителя, наряду с пониманием необходимости использования средств ИКТ, выразили озабоченность присутствием тенденции подмены нахождения решения задачи самим учащимся на угадывание ответа с помощью соответствующих компьютерных систем. После получения ответа, точного или примерного, учащиеся пытаются сформировать решение, что редко является самым продуктивным подходом.

Заключение. В рамках исследования обоснована необходимость повышения уровня компетентности учителя математики в направлении применения задач на готовых чертежах с учетом современного развития ИКТ, описаны некоторые подходы для эффективного повышения уровня этой компетентности.

В процессе проведенного анализа выявлены некоторые проблемы, возникающие при изуче- нии геометрии в школе, построена структура краткосрочных курсов повышения квалификации, разработана примерная схема организации работы с заданиями на готовых чертежах, отмечена возможность сочетания задания на готовых чертежах с геймификацией (игрофикацией) учебного процесса.

В дальнейшем планируется развитие системы курсов повышения квалификации учителей математики и педагогов ДО в плане совершенствования профессиональных компетенций по использованию устных заданий в обучении школьников геометрии с использованием различных обучающих сред.