Совершенствование работы оборудования для противоточной экстракции на основе моделирования процесса

Современные тенденции рационального природопользования предполагают все более широкое применение технологий глубокой переработки пищевого сырья. Одним из направлений реализации таких тенденций является переработка вторичных пищевых ресурсов как дополнительного источника ценных пищевых веществ [1–3]. Непременным этапом такой переработки является экстракция предварительно измельченных и гидратированных вторичных пищевых ресурсов [4,5]. Экстракционный способ извлечения полезных ингредиентов из вторичного сырья широко спространен во многих сферах пищевой промышленности и его совершенствование определяет эффективность работы отрасли [6–8].

Как правило, цель экстракции – извлечение ценных пищевых компонентов из растительного или животного сырья. Так, например, благодаря процессу экстракции, из топинамбура извлекается пектин – вещество, имеющее высокую пищевую ценность. Поскольку. в основе процесса экстракции лежат явления тепло- и массообмена, для прогнозирования результатов работы технологического оборудования необходимо знать влияние различных параметров системы (температура, давление, гидромодуль, степень измельчения сырья) на протекание этих процессов [9, 10–20].

Цель работы состоит в оптимизации процесса экстракции ценных пищевых веществ из растительного сырья путем разработки математической модели процесса экстрагирования на примере извлечения пектина или инулина из такого растительного сырья как, топинамбур, при многоступенчатом противоточном циклическом процессе экстракции. Для этого необходимо учесть эффект обратного перемешивания растворителя, время стока растворителя из твердой фазы в зоне отсутствия орошения, влияние времени выдержки материала на эффективность последующей ступени орошения, и усовершенствовать действующие экстракторы, предназначенных для этих целей.

Материалы и методы

Концентрация наружного раствора от времени в промышленных аппаратах экстракторах типа ДС 70 и НД 1250 напрямую зависит от математической задачи, а так же ее модели дискретной диффузии. Нужно отметить, что решения задач экстрагирования выполнены при допущении, что внутренняя структура частиц изотропна, но это условие не является постоянным. Было замечено, что масличность различных слоев материала в ходе его прессования различна. Одной из причин этого является определенная ориентация и более плотная упаковка белковых молекул в слоях, примыкающих к валу шнекового пресса, что, естественно, свидетельствует и о различиях во внутренней структуре различных слоев. При ступенчатом сбросе давления при экстрагировании сжиженными газами происходит разрушение клеточной структуры наружных слоев частиц, так что внутренняя их структура заведомо анизотропна.

Для получения математической модели дискретной диффузии при многоступенчатом экстрагировании растительного материала с различной степенью вскрытия клеточной структуры из частиц шарообразной формы (соответствует подготовке материала к экстрагированию в виде крупки), состоящей из двух зон с различными коэффициентами диффузии D1

и поверхностного слоя, состоящего из разрушенных клеток с соответственно большим коэффициентом диффузии D2. Из этой двухзонной частицы вещество отводится многократно (многоступенчатое экстрагирование).

Математически задача формулируется следующим образом: требуется решить уравнение нестанционарной диффузии dCj)     fd2Cj)  2 dCj))

= Dk■ бт          dr2    r

V7

^{( т} >  ⁰ , R k - 1 <  ^rk , R = °)

При следующих краевых условиях:

C^k ) ( ^{r, т} ° ) = f ( ^r ) ;

при т = 0 f ( r ) = C_o = const

C ;j' ( R„t ) = C j ²¹ ( R„t )

dc^ =- D Ci^n d r               d r

® C^°^ = °; C ¹ ) (°, _r ) <„

В r                i'

C(2)( R2,T ) = Cn = const

C^Г'( R 2 , T )

dr

Условие (2) – начальное, определяющее распределение концентрации извлекаемого вещества в начальный момент соответствующего периода.

Уравнения (3)–(4) являются математическим выражением граничного условия четвертого рода, определяющего равенства концентраций и потоков массы вещества при хорошем массообменном контакте между ядром и поверхностным слоем.

Выражения (5) – условия симметрии и физической ограниченности распределения извлекаемого вещества.

Условия (6) и (7) являются математическим выражением взаимодействия частиц (семени) с окружающей средой в первом и втором периодах процесса. Не уменьшает общности постановки задачи взятое C п = 0. Таким образом, приведенная формулировка данной комплексной задачи содержит ряд отдельных задач, решения которых порознь известны. В данном случае задача существенно сложнее: рассматривается диффузия вещества в двухслойной частице с попеременным непрерывным и дискретным отводом вещества.

В результате применения методов математической физики получено решение краевой задачи (1)–(7), которое для регулярной стадии процесса и для усредненных значений концентрации можно записать в следующем виде:

Ф 11 = V k D Y 11 ^sin 2 Р 11 ⁺ Р 11 ^{5in 2} / 11 ⁺

1 - kD     . 2    . 2

+ Г—D - sin /nsin An

V kD Yn

Ф 12 = ^kD ^{(sin Р 12 ⁺ 7 k D^kD / 12 cos Р 12 ) ^X

^X ( / 12 ^- sin /12 ^cos / 12 ) ⁺

^{+ k}D sin / 12 ( / 12 cos / 12 ^- sin / 12 ) ^X

C o - C j ) = 1 + ( - 1 ) j M j ) , где

M 1 = 3 k m k R ^ /( sin Р 11 ) ^{2- j} x

1 - Y

x (sin /1 j - /1 jcos /1 j) —x

v                     щ2(kR)

^{x (cos} Р 12 ^- Р 12 ^kR sin Р 12 ) ^-

^- / 12 ^sin2 / 12 [ ^kR Р 12 cos Р 12 ⁺ ( ^kR ⁺ 1 ) sin Р 12 ] ^} Щ 2 ( k R ) = T k D / 12 s ⁱⁿ / 12 ^COs( Jk D / 12 ( ^kR - 1 ) ) ^{+ +} [ ( 1 ^{- k}D ) sin / 12 ^{+ k}D / 12 cos / 12 ] ^X

^{x sin(} Jk D / 12 ( ^kR ^{- 1} ) );

x

² Ж 2 ( ^k R ) sin /11 ( 1 ^- Y ²) Ф 11

n

x

2sin y _nsm y₁₂

_ (1 - Y2) Ф11

x

x exp

-

-   ^F o „

sin Г _п (sin Р и + k D Yr _ncos

M = I

k Dn> ( 1 - k R ) Y 11 sin P 11 (sin / j! - / ц cos / _п) .

D M ^{( 1 )} для остальных i и j

1 — k R   i

M^ при i = j = 1

5 = j - 3 + (к - 1)( 2 - j );

m =

1_i+ (-1)j-(k-1)_ ;

;

i + ( - 1 ) ^j приi = 1; n = i + j - 2;

i = I i + (-1)j + 2 при i > 1;/ =     '

/ 12

i - номер ступени ( i — 1,2,3, ^ J ); j - номер периода на ступени ( j = 1,2) ; k - номер зоны частицы ( k = 1 – ядро, k = 2 – поверхностный слой); c – концентрация диффундирующих веществ; k_c = D , ID 2 ; k R = R ,/ R 2 ; Р = ,/ k D ( k R - 1 ) / ;

Jk_D ( k_R - 1 ) - иррациональное число;

Fo = Dxt/R2 ; Fo = DTj /R2 - числа Фурье.

Таким образом, определено распределение концентраций в каждой из зон на любой ступени и любом периоде на ступени. Пользуясь полученными результатами, можно оценить коэффициенты диффузии реальных материалов по зонам, и, применяя интервальный метод расчета, оценить степень вскрытия клеточной структуры на каждой ступени. Наличие адекватного аналитического описания ступенчатого процесса экстрагирования позволяет осуществить и оптимизацию процесса.

Полученная модель дала возможность разработать аналитическую оценку эффективности дискретной диффузии из двухзонных частиц шарообразной формы в сравнении с непрерывной диффузией при многоступенчатом экстрагировании растительного материала в виде неравенства:

0 <  A <  1, (11)

Здесь Yn - первый положительный рень характеристического уравнения

ко-

1    i +1      .

A = -2 kD2 /11Y ■

3 ф(1 - Y2 )sin /12 - /12 cos /12 x Щ2 (kR ) sin YXX - /11cos Yn

Y_n - положительный корень характеристического уравнения

x

2sin Yu

FT) J

J 2

—

^k R Ж 2 ( ^k R ) sin / 12 ^ф 11 ^ф 12

x

- ( ^kD^kR X ^{2 +} 1 ) = ⁰

^{x e} xp - ZE Y 1^{2 F}o y - 121^^0

*

* = Dt

^O R ^{2 ,}

– время соб- диф    изол , диф     р

ственно диффузии (отвода вещества) на ступени;

t изол – время отсутствия потока вещества через внешнюю поверхность частицы.

Данный подход может быть использован и при делении частицы на произвольное число зон с различной внутренней структурой.

Экстрагирование и адсорбцию в системе твердое тело-жидкость, широко используемые в пищевой промышленности, можно рассматривать с единой позиции массообмена как процессы с противоположными направлениями потоков массы.

Вещество в твердой фазе, подвергаемое экстрагированию, в общем случае состоит из двух частей: удерживаемой сорбционными силами и распределенной, обычно равномерно, в поровом пространстве тела. При сорбции в твердой фазе вещество накапливается за счет собственно сорбции и за счет его диффузии в поровом пространстве. Сказанное предопределяет следующую постановку вопроса: необходимо исследовать диффузионно-сорбционную задачу с внутренним источником массы, зависящим от времени и положительным в случаях адсорбции и экстрагирования.

В общем виде поставленная задача

для частиц шарообразной формы может записана следующим образом:

быть

® С = D дт

д ² C.   2 д C

—51 +--1

д r    r д r

+ a о ( ^т ) ;

т > 0; 0 < r < R

C2 (R ,т) =

C( r ,0 ) = C106 > C20

C1( r ,0 ) = C 06 < C20;

C ( r ,0 ) = 0;

C (0,т) ^ rc;

д^ (0,т)

d r

= 0;

где C , C – текущее и начальное значение

концентрации раствора внутри частиц; C ₂ , C – текущее и начальное значение концен-

трации раствора снаружи частиц; т - время; r – текущее значение радиуса; R - радиус шара; a_c - скорость адсорбции (десорбции); Y – координата, нормальная к поверхности шара.

Формула (14) соответствует экстрагированию, формулы (15) и (16) адсорбции.

Отметим, что в написанную систему изотерма адсорбции не входит, поскольку она характеризует равновесное состояние, т. е. должна быть получена из решения поставленной задачи как предельное состояние системы.

Условия (14) –  (16) соответствуют направлениям потоков массы при экстрагировании и адсорбции, (17) и (18) – общеизвестны. Функция ас (т) отражает изменение скорости адсорбции (десорбции) во времени и, естественно, определяется природой адсорбционных сил, величиной удельной поверхности адсорбента, свойствами адсорбируемого вещества, его концентрацией и другими характеристиками сорбционных свойств системы твердое тело-жидкость.

Если для адсорбции газов (паров) собственно сорбция протекает, очень быстро ( 10 - 8 - 10 - 9 с ), то адсорбция из растворов длится несколько десятков минут, что по порядку величин равно продолжительности реальных диффузионных процессов. Что касается десорбции при экстрагировании, то при некоторых случаях собственно десорбция протекает длительнее процесса экстрагирования. Таким образом, для системы твердое тело-жидкость 0 < а_с ( т ) < а_нс , где 0 < а_нс < гс ( а_{н с} - начальная скорость адсорбции), и поэтому необходимо определять вид этой функции. Выбор здесь ограничен: из функций, при использовании которых возможно решение системы (12)–(18), приведенному условию удовлетворяют лишь функция косинуса, экспонента и функция Гаусса; две последние требуют экспериментального определения входящих в них коэффициентов, но по виду графиков мало отличаются от функции косинуса. С учетом сказанного будем иметь:

ac (т) =

пт

a _нсcos      ,

^{2 т} кс

где т_кс — конечное время собственно сорбции.

В качестве краевого условия (13) для противо-потока, что практически наиболее важно, предлагается принять:

C 2 ( R , т ) = C 20 + ( C 2 k-.-C 20 )sin П!_ ±

2 т ^к    (20)

+5 dC 2 ( ^Г , т )

dY

где C – конечная концентрация наружного раствора; тк - конечное время процесса в целом; 5 - толщина пограничного слоя; знак “плюс” относится к экстрагированию, “минус” к адсорбции.

Алексеев Г.В. и др. Вестник ВГУИТ, 2022, Т. 84, №. 2, С. 27-33 Результаты и обсуждение

Данная функция (20) при С_гк = 0 и

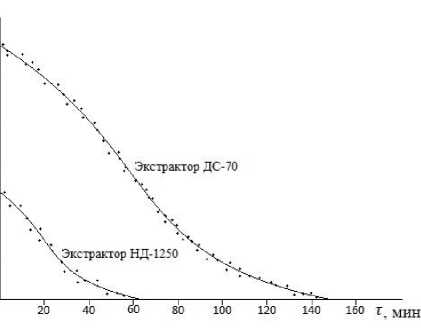
5 = 0 исследована при изучении только одного процесса противоточного экстрагирования, она адекватна изменению концентрации наружного C раствора ² в зависимости от времени ^т в промышленных экстракторах (рисунок 1) и по сравнению с другими функциями обладает тем же преимуществом, что и функция (19).

с 60

5040-зо-2010-

τ, min

Рисунок 1. Зависимость концентрации наружного раствора (мисцеллы) от времени в промышленных аппаратах

Figure 1. The dependence of the concentration of the external solution (miscella) on time in industrial devices

Третий член функции (20) отражает существование пограничного слоя на поверхности сорбента. Введение третьего члена в условие (20) позволяет обосновать его корректность, например, для адсорбции при т ^ 0, C (R,0) ^ 0, что соответствует условию (16), в то время как если бы в условии (20) не было третьего члена, то было бы С2 (R,0) ^ С20 . Последнее может быть объяснено, в частности, тем, что при определенных гидродинамических условиях 5 ^ 0 . Наконец, третий член позволяет привести в соответствие с экспериментом условие (20) путем правильного выбора функции С2 ( Y,т ) = А ( Y )• При т >да С (R, да) ^ C2t ^ С20, так как в этом случае концентрация по толщине пограничного слоя выравнивается, т. е dC^ ( Y, т )/dY = 0.

Поскольку задачи можно было бы усложнить путем введения граничных условий третьего рода, но это привело бы к дополнительному учету лишь конвективного массообмена, что общеизвестно и для современных интенсифицированных процессов экстрагирования и адсорбции малозначимо.

Заключение

Полученные результаты позволяют с высокой степенью достоверности прогнозировать концентрацию наружного раствора в зависимости от времени процесса экстрагирования. Это подтверждается измерениями концентрации экстрагируемого вещества в течение эксперимента и близостью их значений к расчетным. Таким образом, можно считать, что полученное уравнение (20) позволяет провести анализ влияния степени пропитки мисцеллы, взятой с промежуточной ступени противоточного многоступенчатого экстрактора, на эффективность процесса. Благодаря аналитическим расчетам с использованием полученной математической зависимости можно оптимизировать работу оборудования путем внесения изменений в его конструкцию, обеспечивающих влияние рассчитанных технологических параметров на ход процесса