Совместная работа навесной фасадной системы и железобетонного каркаса здания при сейсмическом воздействии

Конструкции навесных фасадных систем уже с конца XX века используются в строительстве. Они применяются как для нового строительства, так и при реконструкции старых зданий. На данный момент наиболее распространенными вариантами наружных ограждающих конструкций являются стены из малоразмерных блоков, светопрозрачные конструкции и навесные фасадные системы (НФС). В России основные виды конструкций НФС с различными видами облицовок обсуждаются многими авторами [1]–[5]. Фасадные конструкции приобрели широкую популярность в современном строительстве, и их анализ на примере новостроек рассматривается в работе Волковой А.А. [6]. Также в практике стали более популярны каркасно–обшивные стены из легких стальных тонкостенных профилей [7].

Однако методики детализированного расчета ограждающих конструкций стали развиваться относительно недавно. Существует несколько нормативных документов, действующих в РФ, в которых поднимается вопрос расчета и проектирования наружных ограждающих конструкций [8]– [12].

В научной литературе к вопросу расчета наружных ограждающих конструкций обращаются чаще. Так в статьях российских ученых [13]–[15] рассматривается вопрос расчета навесных фасадных систем и светопрозрачных конструкций при воздействии статических нагрузок. Тем не Rybakov, V.; Saburov, D.; Gusev, K.; Galyamichev A.

Combined behavior of the hinged facade system and reinforced concrete frame of the building under seismic impact

менее, в статье [16] коллектив авторов выделяет проблему отсутствия в нормативно–технической документации РФ единых норм и правил проектирования НФС с различными видами облицовок. Необходимо отметить, что на момент написания статьи появился новый нормативный документ, посвященный проектированию, монтажу и эксплуатации НФС СП 522 «Системы фасадные навесные вентилируемые» [12].

Более того, вопросы изучения ограждающих конструкций, в частности, навесных фасадных систем, активно поднимаются авторами в других странах. В работах рассматриваются основные принципы правильного проектирования и особенности выполнения статического расчёта НФС с помощью метода конечных элементов [17]–[20].

Важно отметить, что навесные фасадные системы, несмотря на их разнообразие и преимущества, имеют отрицательные стороны применения и проблемы, возникающие при их работе [21], [22]

В статьях [23] рассматривается вопрос работы наружных ограждающих конструкций при динамическом сейсмическом воздействии. Поднимая тему динамических воздействий, хочется отметить, что авторы в своей статье [24] разработали требования к методике определения динамических нагрузок на облицовку здания в составе НФС при ветровых порывах.

В исследовании [25] рассматривается вопрос влияния способа крепления облицовки на расчетную модель несущих элементов системы.

В исследовании [26] поднимается вопрос совместного расчета НФС и каркаса здания. В исследовании делается вывод, что при расчете навесных фасадных систем необходимо учитывать их совместную работу с каркасом здания.

Исходя из обзора существующих научных работ, можно сделать вывод о том, что имеется значительное представление о численном моделировании и расчёте НФС при действии статических нагрузок. Однако, вопрос работы НФС совместно с каркасом зданий при действии динамических нагрузок до конца не изучен. Как правило, НФС рассчитываются в изолированной постановке как при действии статических, так и динамических нагрузок.

Цель работы заключается в исследовании влияния каркасов зданий на НДС конструкции навесных фасадных систем при их совместной работе при сейсмическом воздействии.

Объект исследования – это элементы системы навесной фасадной конструкции.

Предмет исследования – это совместная работа НФС и каркаса зданий при действии сейсмической нагрузки.

2    Materials and Methods

Для проведения научного исследования была использована навесная фасадная система, предназначенная для облицовки зданий и сооружений различного назначения фиброцементными панелями. Основными несущими элементами каркаса являются кронштейны, удерживающие вертикальные направляющие на необходимом вылете от стены, и сами направляющие, к которым крепятся облицовочные панели при помощи иклевого соединения. Несущий кронштейн, опорный кронштейн и направляющий профиль образуют крепёжный блок, представленный на рисунке 1.

Рис. 1 – Общий вид НФС и крепёжного блока

Fig. 1 – General view of the HFS and the mounting block

Для проведения численных расчётов была создана конечно–элементная модель НФС в ПК

SCAD Office . Расчётная схема предусматривалась на 3 пролета здания.

Фрагмент расчётной схемы представлен на рисунке 2.

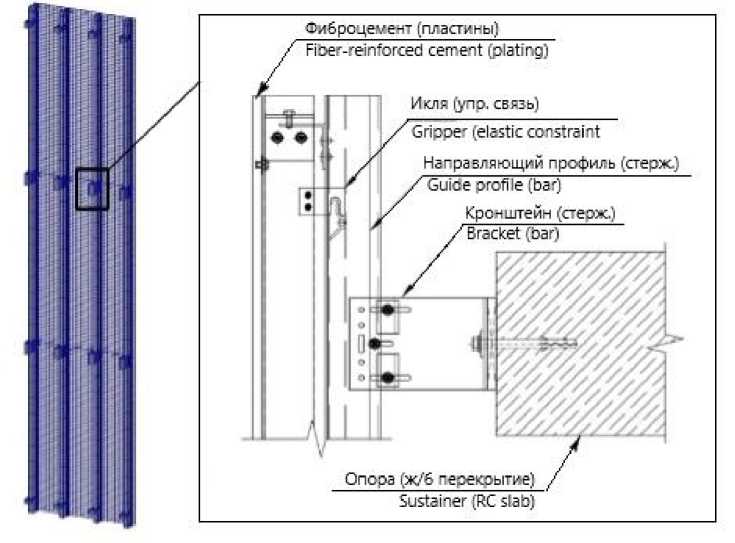
Рисунок 2. Фрагмент расчётной схемы и общий вид НФС в ПК SCAD Office

Figure 2. A fragment of the calculation scheme and a general view of the HFS in the SCAD Office

В качестве материала для подконструкции НФС используется алюминиевый сплав AlMgSi (6060) Т66 в соответствии с государственным стандартом ГОСТ 22233–2018 «Профили прессованные из алюминиевых сплавов для ограждающих конструкций» [27]. Модуль упругости на растяжение/сжатие 69000 МПа, на сдвиг 26000 МПа. Коэффициент Пуассона равен 0.33.

Основные нагрузки, действующие на навесную фасадную систему приведены в таблице 1.

Таблица 1. Нагрузки, действующие на навесную фасадную систему Table 1. Loads acting on the hinged faсade system

	Вид нагрузки / Type of load	Значение нагрузки, кгс/м2/ Load value, kgf/m2
1	Собственный вес алюминиевых конструкций / Dead–weight of aluminum structures	Учитывается ПК SCAD исходя из плотности 2700 кг/м3 / The SCAD PC is taken into account based on the density of 2700 kg/m3
2	Собственный вес облицовки / Dead–weight of cladding	19.8

В качестве модели для исследования были смоделированы два здания с железобетонным каркасом различной формы: первое – квадратное в плане с несущими колоннами (рис. 3), второе – прямоугольное со стеновой конструктивной схемой (рис. 4). Размеры квадратного здания в плане: 31х31 м; прямоугольного: 31х24 м. Высота этажа в обоих зданиях равна 3 м. Модели зданий были основаны на ранее использованных конструктивных решениях для строительства в сейсмически опасных районах. Шаг сетки и конечных элементов (КЭ) в моделях составлял 0.6 м.

В обоих зданиях использовался бетон класса B30 в соответствии с государственным стандартом ГОСТ 26633–2015 «Бетоны тяжелые и мелкозернистые» [28]. Модуль упругости 32.5 МПа. Коэффициент Пуассона равен 0.2. Оба каркаса имели стены подземной части толщиной 300 мм, стены надземной части толщиной 250 мм, перекрытия толщиной 250 мм, фундаментную плиту толщиной 600 мм, сваи сечением 400х400 мм. Квадратное в плане здание предусматривало колонны и балки сечением 450х450 мм.

Основные нагрузки, действующие на здание приведены в таблице 2. Нагрузка от воздействия ветра не учитывалась, согласно требованию нормативного документа по проектированию в сейсмически опасных районах СП 14.13330.2018 «Строительство в сейсмических районах» [29].

Таблица 2. Нагрузки, действующие на здание

Table 2. Loads acting on the building

	Вид нагрузки / Type of load	Значение нагрузки, кгс/м2/ Load value, kgf/m2
1	Собственный вес ЖБ / Dead–weight of reinforced concrete	Учитывается ПК SCAD исходя из плотности 2500 кг/м3 / The SCAD PC is taken into account based on the density of 2500 kg/m3
2	Собственный вес кровли / Dead–weight of roofing system	246.2
3	Собственный вес пола подвала/первого этажа/типового этажа / Dead–weight of basement flooring/ground flooring/standard flooring	105.3/264.3/95.1
4	Собственный вес перегородок из кирпича / Dead–weight of brick parting wall	140
5	Собственный вес ограждающих стен (без НФС) / Dead– weight of non–bearing wall (without NSF)	2276
6	Собственный вес парапетов / Dead–weight of barrier wall	911
7	Полезная нагрузка МОП/Жилые помещения / Running load of common facilities / domestic premises	367.2/180
8	Вес снега / Snow load	214

Сбор расчётных нагрузок, действующих на навесную фасадную системы и каркасы зданий осуществлялся на основании нормативного документа, регламентирующего используемые при расчете нагрузки СП 20.13330.2016 «Нагрузки и воздействия» [30].

Этажность зданий подобрана с целью обеспечения одинаковой первой собственной частоты колебаний для обоих каркасов. В результате высота надземной части квадратного здания составляет 27 метров (9 этажей), а прямоугольного 45 метров (15 этажей) без учета надстройки лестнично–лифтового узла. Собственные частоты зданий: 1.197 Гц (квадратное), 1.166 Гц (прямоугольное). Расхождение составило 2.6 %.

Для проведения совместного расчёта НФС в составе каркасов железобетонных зданий вышеупомянутые конечно–элементные модели каркасов зданий и НФС были объединены при помощи «режима сборки». При этом граничные условия закрепления НФС к каркасу зданий были приняты аналогичными изолированному подходу к расчёту. Анкерное соединение кронштейнов и перекрытий зданий было выполнено при помощи ввода абсолютно жестких тел (АЖТ). Узлам кронштейнов и перекрытий были заданы объединения перемещений – при упорах кронштейнов в перекрытие и запретам поворотов, обуславливающие работу НФС и взаимодействие горизонтальных несущих элементов здания с кронштейнами фасадной системы. Сгущение сетки конечных элементов перекрытий расчётных моделей каркасов зданий было выполнено при помощи разбиения на треугольные КЭ таким образом, чтобы узлы кронштейнов НФС совпадали с сеткой перекрытий. Наименьший шаг сетки при этом составляет 0.03 м. В начале исследования в обоих расчётных случаях НФС была расположена на верхних этажах каркасов зданий.

Общие виды конечно–элементных моделей зданий и присоединенных к ним НФС приведены на рисунках 3–4.

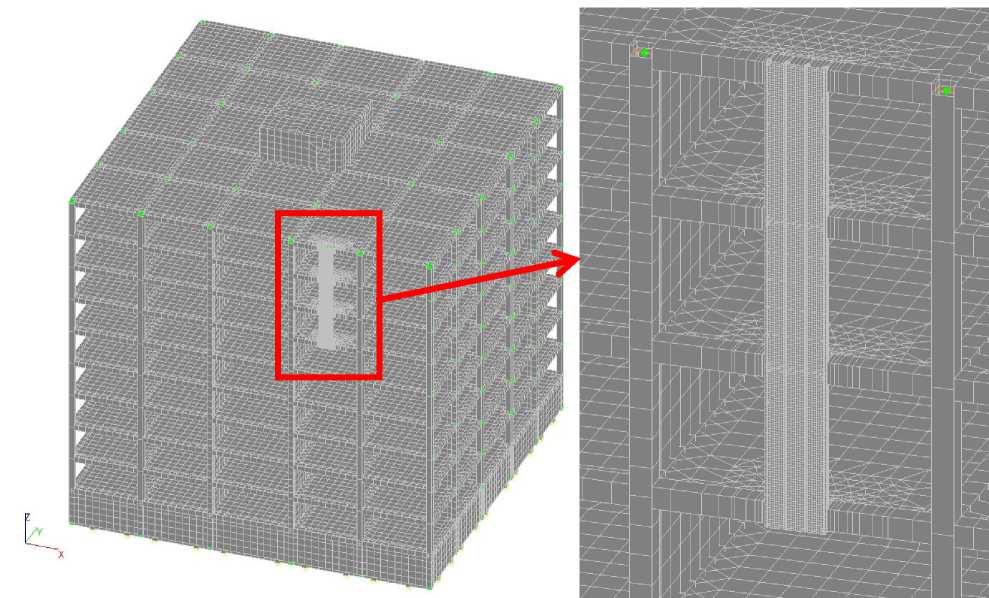
Рис. 3 – Общий вид здания (схема №1) с присоединенной навесной системой Fig. 3 – General view of the building (scheme No. 1) with attached hinged system

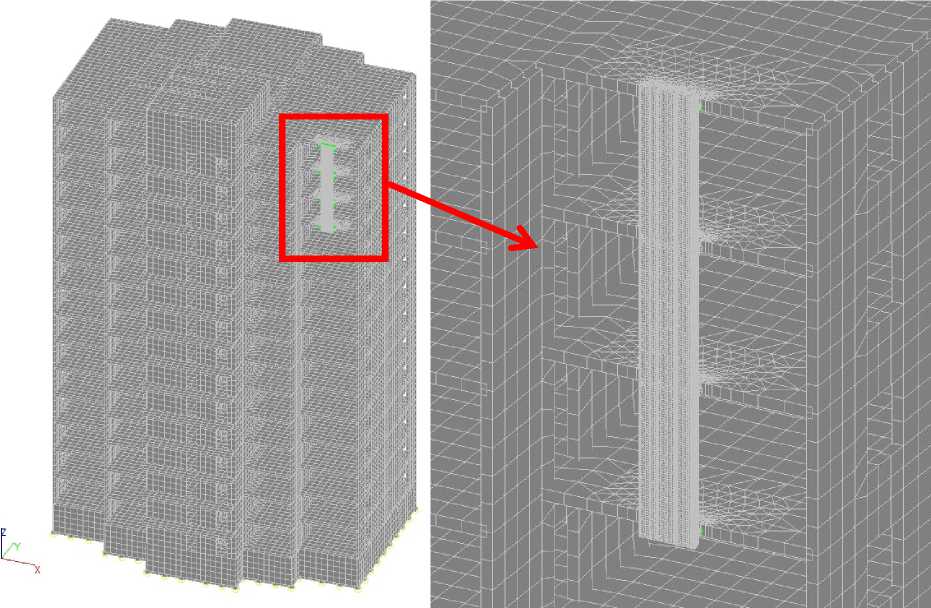
Рис. 4 – Общий вид здания (схема №2) с присоединенной навесной системой Fig. 4 – General view of the building (scheme No. 2) with attached hinged system

Как для изолированной, так и для совместной постановки задачи использовались одинаковые параметры сейсмической нагрузки. Расчет выполнялся на расчетное землетрясение (РЗ). Расчётная сейсмичность площадки строительства, принятая в расчёте составляет 8 баллов.

Строительство в сейсмических районах регулируется нормативным документом СП 14.13330.2018 «Строительство в сейсмических районах. Актуализированная версия СНиП II–7– 81» [29].

Для вычисления расчетной сейсмической нагрузки были приняты следующие коэффициенты:

Коэффициент, учитывающий назначение сооружения и его ответственность (Таблица 5.3. СП 14.13330.2018, здание относится к жилым и административным зданиям высотой больше 75 м):

K 0 = 1.1 (1)

Коэффициент, учитывающий допускаемые повреждения зданий и сооружений (Таблица 5.4, здания и сооружения, в конструкциях которых повреждения или неупругие деформации не допускаются):

K = 1.0 (2)

Коэффициент, учитывающий способность зданий и сооружений к рассеиванию энергии (Таблица 5.5, коэффициент для каркасных бессвязевых зданий, стеновое заполнение которых не оказывает влияния на их деформируемость):

K = 1.3 (3)

В качестве масс были назначены статические нагрузки (собственный вес конструктивных элементов навесной фасадной системы). В расчете были учтены до 120 первых собственных форм колебаний.

Далее были выполнены динамические расчёты НФС: сначала в изолированной постановке, а затем – в составе двух каркасов зданий на действие сейсмической нагрузки. Для уточнения результатов исследования совместный расчёт был проведён для различного положения фасадной системы по высоте каркасов зданий. В первую очередь, был выполнен модальный анализ и определены собственные частоты колебаний НФС, как в изолированной постановке, так и при совместном расчёте. Далее были рассмотрены полученные при расчете напряжения и усилия в наиболее нагруженных элементах фасадной системы.

При анализе результатов были использованы 2 особые комбинации воздействий, включающие различные направления вектора сейсмического воздействия: в горизонтальной плоскости фасада (по оси Х) и из плоскости фасада (по оси Y).

3    Results and Discussion

Для сравнения полученных результатов с результатами изолированного расчета НФС были определены максимальные напряжения, возникающие в направляющих профилях и кронштейнах, а также максимальные усилия, возникающие в иклевом креплении. Также, исходя из модального анализа, были определены собственные частоты колебаний НФС. Полученные результаты сведены в таблицу 3.

Таблица 3. Сравнение результатов изолированного и совместного расчета Table 3. Comparison of the results of isolated and joint calculation

Тип схемы / Type of scheme	Максимальные напряжения в элементах НФС, МПа / Maximum stresses in the elements of HFS, MPa		Максимальное усилие в икле, Н / Maximum force in gripper, N	Первая собственная частота, Гц (НФС) / The first natural frequency, Hz (HFS)
	Кронштейн / Bracket	Направляющая / Guide profile
В составе кв. в плане каркаса / As part of the square in plan frame	363.64	76.096	274.42	7.578
В составе пр. в плане каркаса / As part of a rectangular in plan frame	195.79	39.336	155.45	7.119
Изолированная / Isolated	139.21	16.16	47.77	7.71

При расчете выяснилось, что наиболее неблагоприятной для работы НФС является особая комбинация нагрузок с вектором сейсмического воздействия, направленной в горизонтальной плоскости фасада (по оси Х).

Расчет показал, что наибольшие напряжения, возникающие в навесной фасадной системе, больше, чем аналогичные напряжения при изолированном расчете. Рост напряжений происходит в пределах от 1.4 до 5.8 раз. При этом первая собственная частота колебаний при совместном расчете меньше, чем при изолированном: в квадратном здании на 1.7%, в прямоугольном на 7.6%.

Для определения влияния положения навесной системы на ее НДС и собственные частоты колебаний, были проведены дополнительные расчеты с изменением положения НФС по высоте каркаса зданий. В квадратном здании рассмотрено несколько вариантов расположения системы: на 1–3 этажах, 4–6 и 7–9 этажах. В прямоугольном здании рассматривались положения системы на 1–3, 4–6, 7–9, 10–12 и 13–15 этажах.

Таблица 4. НДС навесной системы при изменении положения в квадратном здании Table 4. Strain–stress distribution of the hinged system when changing the position in a square building

Положение НФС / Location of the HFS	Максимальные напряжения в элементах НФС, МПа / Maximum stresses in the elements of HFS, MPa		Максимальное усилие в икле, Н / Maximum force in gripper, N	Первая собственная частота, Гц (НФС) / The first
	Кронштейн / Bracket	Направляющая / Guide profile

				natural frequency, Hz (HFS)
7–9 этажи / 7–9 floors	363.636	76.096	274.42	7.578
4–6 этажи / 4–6 floors	335.669	83.709	288.03	7.578
1–3 этажи / 1–3 floors	307.087	84.861	283.34	7.578

Таблица 5. НДС навесной системы при изменении положения в прямоугольном здании Table 5. Strain–stress distribution of the hinged system when changing the position in a rectangular building

Положение НФС / Location of the HFS	Максимальные напряжения в элементах НФС, МПа / Maximum stresses in the elements of HFS, MPa		Максимальное усилие в икле, Н / Maximum force in gripper, N	Первая собственная частота, Гц (НФС) / The first natural frequency, Hz (HFS)
	Кронштейн / Bracket	Направляющая / Guide profile
13–15 этажи / 13–15 floors	195.789	39.336	155.45	7.119
10–12 этажи / 10–12 floors	188.302	43.052	163.37	7.119
7–9 этажи / 7–9 floors	186.241	50.858	182.65	7.119
4–6 этажи / 4–6 floors	170.875	51.589	180.161	7.119
1–3 этажи / 1–3 floors	161.396	47.188	163.52	7.12

При изменении положения НФС по высоте каркасов, напряжения и усилия в элементах системы изменяются. При этом, если с увеличением высоты расположения НФС напряжения, возникающие в кронштейнах, увеличиваются, то в направляющем профиле и иклевом креплении изменения напряжений и усилий не имеют закономерный характер. В целом, изменения напряжений в элементах НФС находятся в пределе 25%. При этом первая собственная частота колебаний навесной фасадной системы не изменяется при изменении положения по высоте каркаса здания.

Результаты расчетов представлены в форме графиков зависимости напряжений и усилий, в зависимости от расположения системы.

12 floors

15 floors

Расположение НФС / Location of the HFS

Прямоугольный каркас / Rectangularframe

Квадратный каркас / Square frame

4-6 этажи / 4-6   7-9 этажи / 7-9

floors             floors

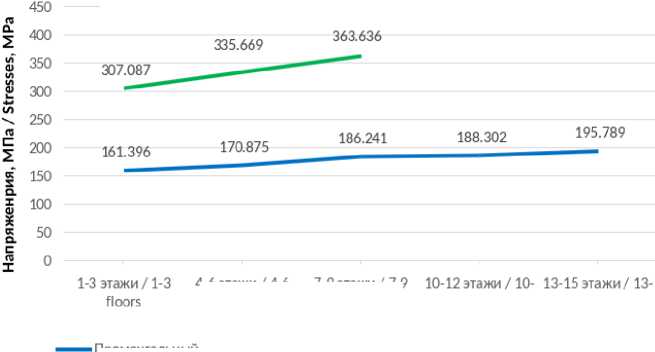
Рис. 6 – График максимальных напряжений в кронштейне

• Fig. 6    – Graph of maximum stresses in the bracket

  

  я           1-3 этажи /1-3   4-6 этажи / 4-6   7-9 этажи / 7-9 10-12 этажи / 10- 13-15 этажи /13-

  floors             floors             floors            12 floors          15 floors

  Расположение НФС / Location of the HFS

  
  

^^—Прямоугольный каркас / Rectangular frames—Квадратный каркас / Square frame

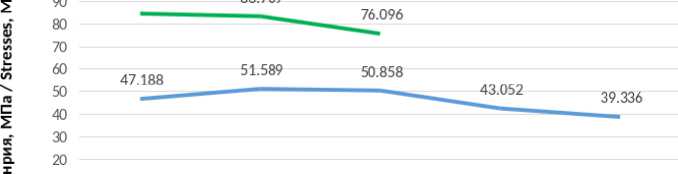
Рис. 7 – График максимальных напряжений в направляющем профиле

• Fig. 7    – Graph of maximum stresses in the guide profile

350 3(Ю   283J4___288;O^^^k42 250

Z

8 о Li.	___________________180.161________182.65__ _____^3.37        i55 45 150                               —
X к s 1	100 50 0

1-3 этажи/1-3 4-6 этажи/4-6 7-9этажи/7-9 10-12 этажи/ 13-15 этажи/ floors           floors           floors 10-12 floors 13-15 floors

Расположение НФС / Location of the HFS

^^—Прямоугольный каркас / Rectangular frame ""Квадратный каркас /Square frame

Рис. 8 – График максимальных усилий в икле Fig. 8 – Graph of maximum effort in the gripper

Графики показывают слабую зависимость напряжений от расположения навесной системы.

Также рассматривались относительные перемещения, возникающие в навесной системе при ее различных положениях.

Таблица 6. Относительные перемещения НФС в плоскости фасада, мм

Table 6. Relative displacements of the HFS in the plane of the facade, mm

Положение НФС / Location of the HFS	Относительные перемещения в НФС (ось Х), мм / Relative displacements in HFS (axis X), mm
	Квадратный в плане каркас / Square in plan frame	Прямоугольный в плане каркас / Rectangular in plan frame
13–15 этажи / 13–15 floors	–	10.134
10–12 этажи / 10–12 floors	–	11.526
7–9 этажи / 7–9 floors	30.837	13.904
4–6 этажи / 4–6 floors	33.771	14.787
1–3 этажи / 1–3 floors	36.655	15.192

Таблица 7. Относительные перемещения НФС из плоскости фасада, мм

Table 7. Relative displacements of the HFS from the facade plane, mm

Положение НФС / Location of the HFS	Относительные перемещения в НФС (ось Y), мм / Relative displacements in HSF (axis Y), mm
	Квадратный в плане каркас / Square in plan frame	Прямоугольный в плане каркас / Rectangular in plan frame
13–15 этажи / 13–15 floors	–	5.055
10–12 этажи / 10–12 floors	–	5.171
7–9 этажи / 7–9 floors	5.306	6.473
4–6 этажи / 4–6 floors	5.165	6.909
1–3 этажи / 1–3 floors	4.304	6.042

Таблица 8. Вертикальные относительные перемещения НФС, мм

Table 8. Vertical relative displacements of the HFS, mm

Положение НФС / Location of the HFS	Относительные перемещения в НФС (ось Z), мм / Relative displacements in HSF (axis Z), mm
	Квадратный в плане каркас / Square in plan frame	Прямоугольный в плане каркас / Rectangular in plan frame
13–15 этажи / 13–15 floors	–	5.452
10–12 этажи / 10–12 floors	–	5.469
7–9 этажи / 7–9 floors	5.738	5.688
4–6 этажи / 4–6 floors	6.101	5.893
1–3 этажи / 1–3 floors	6.657	6.265

Результаты расчета показывают, что чем выше навесная система расположена в здании, тем меньшие перемещения в ней возникают. Так в прямоугольном здании наблюдается снижение суммарных перемещений на 32%, а в квадратном на 15%. Аналогичная ситуация с некоторой погрешностью наблюдается и в перемещениях вдоль осей.

Отобразим результаты расчетов в форме графиков зависимости перемещений от расположения системы.

1-3 этажи /1-3 4-6 этажи / 4-6 7-9 этажи / 7-9

floors floors floors

Расположение НФС / Location of the HFS

10-12 этажи / 10-12 floors

13-15 этажи / 13-15 floors

Прямоугольный каркас/Rectangularframe        Квадратный каркас /Squareframe

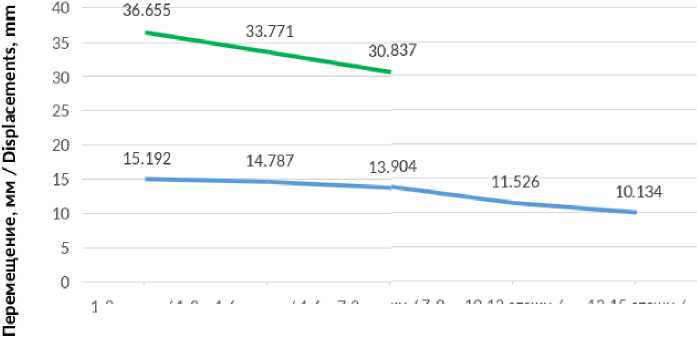
Рис. 9 – График относительных перемещений НФС в плоскости фасада

Fig. 9 – Graph of relative displacements of the HVF in the plane of the facade

floors floors

Расположение НФС / Location of the HFS

10-12 этажи/

10-12 floors

13-15 этажи/

13-15 floors

Прямоугольный каркас / Rectangular frame Квадратный каркас / Square frame

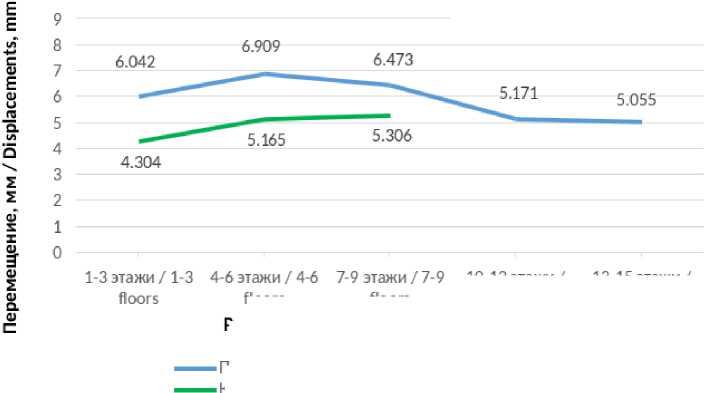
Рис. 10 – График относительных перемещений НФС из плоскости фасада

• Fig. 10    – Graph of relative displacements of the HFS from the facade plane

E    8

E. 75

S    7      6.657

О

i 4

1-3 этажи/1-3 4-6 этажи/4-6 7-9 этажи/7-9 10-12 этажи/ 13-15 этажи/

2               floors           floors           floors 10-12 floors 13-15 floors

• о.                     Расположение НФС / Location of the HFS

E

Прямоугольный каркас / Rectangular frame

Квадратный каркас / Square frame

Рис. 11 – График вертикальных относительных перемещений в НФС

• Fig. 11    – Graph of vertical relative displacements of the HFS

Графики показывают незначительную зависимость перемещений от расположения навесной системы.

4    Conclusions

Основные результаты работы:

• 1.    При совместном расчете НФС с каркасом здания на сейсмическое воздействие усилия и напряжения, возникающие в элементах системы для рассматриваемого в настоящей статье случая, увеличиваются в пределах от 1.4 до 5.8 раз.

• 2.    При изменении положения НФС по высоте каркаса здания, усилия и напряжения, возникающие в элементах системы, различаются. Изменения находятся в пределах 30%. Выявлено, что графики зависимости напряжений в подсистеме по высоте здания имеют незначительно изменяющийся характер, что говорит о возможности учета совместности работы НФС с несущим каркасом здания с помощью уточняющих коэффициентов, которые возможно вывести при выполнении дальнейших исследований.

• 3.    Выявлено, что первая собственная частота колебаний НФС при совместном расчете навесной фасадной системы со зданием уменьшается по сравнению с изолированным расчетом. В прямоугольном в плане здании уменьшение составило 7.6%, а в квадратном 1.7%; при этом первая собственная частота колебания НФС является десятой собственной частотой совмещенной модели и не зависит от положения системы в здании.

• 4.    Относительные горизонтальные и вертикальные перемещения в навесной системе при ее расположении на нижних этажах здания выше, чем аналогичные перемещения в навесной системе при ее расположении на верхних этажах здания на величину от 16% до 34%.

5    Fundings

Исследование выполнено за счет гранта Российского научного фонда № 23–29–00564, –29–00564/