СОВМЕСТНОЕ ОПЕРАТИВНОЕ ПЛАНИРОВАНИЕ ИЗМЕРИТЕЛЬНЫХ И ВЫЧИСЛИТЕЛЬНЫХ ОПЕРАЦИЙ В КИБЕРФИЗИЧЕСКИХ СИСТЕМАХ

Ядром цифровой экономики являются кибер-физические системы (КФС), включающие в свой состав измерительные, телекоммуникационные и управляющие подсистемы [1, 2]. Под КФС далее будем понимать централизованную и/или распределенную аппаратно-программную систему, реализующую физические и инфокоммуникационные процессы сбора, обработки, накопления, хранения, поиска, защиты, распространения и использования данных и информации и взаимодействующую с объектами реального мира через физические процессы [1, 3]. На основе КФС в мире активно разрабатывают "умные" производства, энергетику, транспортные системы, системы обеспечения безопасности жизни и т.д.

Представленные системы позволяют синтезировать технологии управляемой самоорганизации реконфигурацией (модернизацией) "умных" городов. Важным этапом разработки программ управления инфраструктурой в подобных большеразмерных территориально распределенных системах является анализ данных, поступающих из различных источников. Это может быть статус выполнения операций или состояния элементов инфраструктуры: к примеру, направление движения множества подключенных к информационной системе автомобилей, степень готовности партий различных изделий, интенсивность функционирования производственного оборудования, информация от датчиков, передающих сведения о нагрузке на источники энергии. Внедрение, применение и разработка рациональных (в т.ч. скоординированных) программ управления позволяют оптимизировать нагрузку на подсистемы "умных" городов. Это дает возможность снизить электропотребление, а также выбросы вредных веществ в атмосферу.

Таким образом, в подобных системах определяющую роль играют интеллектуальные самоуправляемые измерительно-вычислительные подсистемы КФС. В статье, как уже указывалось ранее, основное внимание уделяется важнейшему классу задач, возложенных на КФС, а именно задачам навигационного обеспечения их функцио- нирования [1, 2, 4]. В число этих задач традиционно включают задачи проведения измерений траекторий движения как обслуживаемых объектов (ОбО), так и КФС, а также задачи обработки (первичной, вторичной, третичной) и анализа полученных данных и информации. На основе решения данных задач осуществляется прогнозирование местоположения рассматриваемых объектов в будущие моменты времени. Перечисленные задачи навигационного обеспечения на практике решаются с определенной периодичностью (циклически), т.к. из-за постоянно возникающих возмущающих воздействий, оказываемых на ОбО и КФС, происходят их отклонения от плановых траекторий. А для этого процессы выполнения измерительновычислительных операций (ИВО) должны быть заранее спланированы. Следует отметить, что к настоящему моменту времени достаточно подробно исследованы задачи парного взаимодействия ОбО с КФС и только применительно к измерительным операциям. Задачи совместного оперативного планирования ИВО, выполняемых группой КФС, до сих пор никем не рассматривались. Все сказанное позволяет говорить о научной новизне и актуальности тематики, рассматриваемой в данной статье.

ЛОГИКО-ДИНАМИЧЕСКИЕ МОДЕЛИ СОВМЕСТНОГО ОПЕРАТИВНОГО ПЛАНИРОВАНИЯ ИЗМЕРИТЕЛЬНОВЫЧИСЛИТЕЛЬНЫХ ОПЕРАЦИЙ, ВЫПОЛНЯЕМЫХ КФС

Для содержательной и формальной постановки задачи совместного оперативного планирования измерительно-вычислительных операций, выполняемых группировкой КФС, введем следующие ~~  ~ множества. Пусть A = {At, г g N} — множество ОбО, входящих в состав группировки и производящих совместное решение целевой задачи (например, мониторинг состояния эколого-экономических объектов (ЭЭО)).

Введем множество КФС: B = { B j , j g M }, M = {1,..., m } . Допустим, что на ОбО и КФС установлены унифицированные аппаратно-программные средства информационного взаимодействия. Также введем обобщенное множество взаимодействующих объектов (ВО) B = { B l } ; l , i , j g M ; M = N U M = {1,..., m} и множество операций взаимодействия (ОВ)       D ⁽ i ) = { D⁽ _Y i ) , у Gф } ,

Ф = {1,..., s.}.

Произведем формализацию задачи совместного оперативного планирования ИВО в КФС.

Для этого мы предпримем логико-динамическую интерпретацию процессов выполнения операций в сложных технических системах, частным случаем которых является КФС [5–7].

Логико-динамическая модель управления операциями взаимодействия (в том числе и вычислительными операциями) в КФС (модель Мо )

Мо = ulo'(t)|x У = Z r.j(t)■

j = 1

x (04 1 o ) = 0, x i^ t f ) = a^, m s i

XX < P^, i = 1 у = 1

X Z u ';;< P'-'¹¹, u ; ;\(< ) g {o,1}, j = 1 7 = 1

u (o) i γ j

Z ("«’ - xi:') + a Gr i, 1

+ П ( a ^ - x^) в еГ„ 2

= 0,

i , j = 1,..., m ; i ^ j ; у = 1,..., s .

(o)

где xiγ — переменная, характеризующая состояние выполнения ОВ D(i); a(o), a(o), a(o) — заданные γ γ iα iβ объемы выполнения операций DYi), d^_i), D^); ui(γo)j (t) — управляющее воздействие; ui(γo)j (t)= 1, если операция Dγ(i) выполняется, ui(γo)j (t)= 0 — в противоположном случае; ГiY 1, ГiY2 — множества номеров операций взаимодействия, проводимых с объектом Bi , непосредственно предшествующих и технологически связанных с операцией Dγ(i) с помощью логических операций "И", "ИЛИ"

(o,1) (o,2)

соответственно; P_j , P_i — заданные константы, характеризующие технические ограничения, связанные с функционированием КФС в целом; r _ij ( t ) — известная матричная временнáя функция, с помощью которой задаются пространственновременные ограничения, связанные с взаимодействием объектов B _i (либо B _k ) с B _j , данная функции принимает значение 1, если B_i попадает в заданную зону взаимодействия B _j , 0 — в противоположном случае.

Логико-динамическая модель управления параметрами измерительных операций, проводимых в КФС (модель Ме )

Me =

u (^e) ( t )| x (^g) = F, ( t ) x (^g) ;

y j¹ ) ( t ) = d т ( t ) X (^g) + $ ^e) ;

m т

Z.=-Z. F.-F"Z.-yydj.   ;

i             i i i i                       i γ j 2

J = 1 Y er ,       ^

, * j; i, j e Ml; 0 < u^ < cYU^j где xi(g) — вектор состояния ОбО Bi ; Fi(t) — заданная матрица, характеризующая динамику изменения переменных (вычисляемых параметров), описывающих состояние ОбО (например, их пространственное положение, либо состояние его бортовых систем); ξj(e) — некоррелированные ошибки измерений параметров ОбО, проводимых с использованием технических средств Bj КФС; предполагается, что ошибки измерений подчиняются нормальному закону распределения с нулевым математическим ожиданием и дисперсией, равной оj; DY) eD(1); uY,(t) — управляющее воздействие, задающее интенсивность проведения измерений параметров y(ji) (t) ОбО (например, дальности до ОбО, температуры и влажности на борту ОбО), которые дистанционно проводятся с помощью технических средств КФС Bj; cY — заданные величины, характеризующие техниче- ские возможности средств Bj при проведении операции Dγ~(i) ; Z i — матрица, обратная по отношению к корреляционной матрице Ki (t) ошибок оценки вектора состояния ОбО B,; Г, — множество операций взаимодействия, проводимых КФС с ОбО Bi ; dj (t) — заданный вектор, определяющий особенности технической реализации уравнения измерителя КФС Bj ; Ki0 — значение Ki (t) в начальный момент времени t = 10; О2, — заданная точность определения γ -й компоненты вектора состояния xi(g) (t) ОбО. Основное отличие модели (2) от ранее предлагаемых состоит в том, что в ней операции измерения параметров состояния ОбО через ограничения на управляющие воздей-(e)

ствия u Y j непосредственно связываются с измерительно-вычислительными операциями, выполняемыми КФС, задаваемыми в модели (1). Это позволяет исследовать с единых системных позиций задачу планирования ИВО как процессов сбора передачи и обработки данных, так и задачи планирования измерений параметров контролируемых объектов.

Показатели качества планирования функционирования КФС.

Оценивание качества процессов программного управления ИВО КФС (или по-другому, качества оперативного планирования ИВО) можно проводить с использованием различных критериальных (целевых) функций [6, 8]. Приведем для примера некоторые из них:

m   ^s i

J (o) = j SS ^ [ a 1 0

1 = 1 у = 1

- х , Y ⁰⁾( t f )] ² +

tf

m

• Xj n_ir^(т ) u oj ^{( t )d T} f , ¹ * ^j ; j = 1 1 0

J 2^e) = b Y K , ( t f ) b_Y ;

t mm     ^f

Ji" = ZSSJ u Yj (T Ж j#i, i=1 j=1 yeD(,) 10

где η γ(τ) — известные монотонные функции времени, которые выбираются с учетом заданных директивных сроков начала (конца) выполнения ОВ ОбО с КФС B . Показатель (3) вводится в том случае, если необходимо оценить полноту выполнения требуемого объема ОВ, входящих в техно- логические циклы управления (ТЦУ) ОбО и КФС, а также величину суммарного штрафа за невыполнение заданных директивных сроков выполнения операций. Для ОбО, в качестве которых будем рассматривать приборные комплексы (ПрК), решающие задачи мониторинга состояния заданных объектов окружающей среды (ООкС), особую значимость имеют операции, связанные с оцениванием их местоположения, которые в свою очередь позволят определить местоположение ООкС. В связи с этим величина показателя качества J2(e) характеризует точность определения γ-й компоненты вектора x(g) (b = ||00...1...00||T — заданный вспомогательный вектор, выделяющий в корреляционной матрице Ki (t) требуемый элемент с номером γ). Показатель J3(e) характеризует суммарные затраты ресурсов, направляемых на проведение измерительных операций.

МНОГОКРИТЕРИАЛЬНОЕ ОЦЕНИВАНИЕ ПЛАНОВ И ФОРМАЛЬНАЯ ПОСТАНОВКА

ЗАДАЧИ

Для успешного решения возложенных на КФС задач необходимо: обеспечить соответствующий уровень автономности, качества и оперативности управления; провести полный перечень работ по комплексной автоматизации и интеллектуализации процессов управления в различных условиях функционирования.

Многочисленные исследования, проведенные в данной области, показали [6, 9], что полимо-дельное описание и многоэтапные интерактивные процедуры в рамках соответствующей интегрированной системы поддержки принятия решений удовлетворяют этому. В целях повышения обоснованности и оперативности принятия решений авторами предлагается в автоматизированном режиме производить интеграцию явных и неявных знаний экспертов о разрабатываемых планах.

Алгоритм проведения опроса и методика описаны в работах [10, 11]. Перечислим ключевые шаги.

Шаг 1. Формирование множества лингвистических шкал для J 1 – J 3 и результирующего показателя качества сопоставимых планов измерительных операций КФС.

Шаг 2. Построение ортогонального плана опроса экспертов и проведение экспертного опроса (ответы на вопросы продукционных правил).

Шаг 3. Построение результирующего показателя качества сопоставимых планов.

В соответствии с модифицированной авторами методикой показатели качества J 1 – J 3 (см. (3), (4)) приводятся к терминальному виду. Далее происходит формирование нового результирующего показателям (5) и замена (4)

Jres w=3          w=3 w=3

= ^A + ^ ^ p^Jp + ^^ ^A p , f^Jp^Jf + ^ 1,2,3 ^J 1 ^J 2 ^J 3 - ⁽⁵⁾

p = 1             p = 1 f = 1

f * p

На основе изложенного метода показатель качества (5) позволяет произвести многокритериальное оценивание разрабатываемых планов измерительно-вычислительных операций, а также учесть явные и неявные знания экспертов об этом процессе.

Для решения сформулированной задачи оптимального программного управления воспользуемся методом локальных сечений, предложенным проф. В.Г. Болтянским и представляющим собой одну из разновидностей методов, реализующих принцип максимума Л.С. Понтрягина для случая задания смешанных ограничений. С помощью ограничений такого вида удалось (см. формулы (1) и (2)) в разработанной модели задать альтернативные варианты технологий выполнения ИВО, а также в последующем синтезировать наилучшие их варианты одновременно с синтезом соответствующих программ управления КФС [12, 13]. Кроме того, в моделях данного класса удалось впервые в явном виде связать измерительные и вычислительные операции, выполняемые КФС. С использованием метода локальных сечений также удалось исходную задачу оптимального управления свести к двухточечной краевой задаче, связанной с процессом поиска начальных условий для соответствующей сопряженной системы [8]. В результате численного решения данной краевой задачи комбинированным методом последовательных приближений Крылова—Черноусько совместно с методом ветвей и границ одновременно синтезируется технология выполнения ИВО, а также для синтезированной технологии вырабатывается план выполнения ИВО [6, 7, 12, 14].

Кратко остановимся на основных шагах предлагаемого алгоритма решения задачи совместного оперативного планирования ИВО, выполняемых группировкой КФС.

Шаг 1. Выполняется опрос эксперта по представленной в работах методике [10, 11].

Шаг 2. Выполняется интеграция многокритериального представления экспертного мнения (5) в исходную задачу (1).

Шаг 3. Выполняется реализация метода последовательных приближений (Крылова—Черноусько) совместно с методом ветвей границ для ликвидации прерываний для тех ОВ, которые недопустимы по технологии управления КФС: задается диспетчерское решение; происходит поиск плана ИВО, проверка краевых условий в конечный момент времени, расчет условий трансверсальности для сопряженной системы уравнений; выполняется "обратный ход" (интегрирование сопряженной системы уравненийи) и поиск первого приближения начальных условий в начальный момент времени для сопряженной системы уравнений, соответствующего заданному диспетчерскому плану.

Далее выполняется поиск оптимальной программы функционирования КИС в "прямом" направлении на основе максимизации функции Гамильтона. Процедура выполняется до тех пор, пока изменения обобщенного показателя качества не будут удовлетворять следующему условию:

I JP * 1) - J p ’| <  « 1 ,                    (6)

где ε1 — заданная величина, r = 0, 1,.... Если ус ловие не выполняется, то происходит повторение шага 3. При этом в качестве диспетчерского управления используется управление (план ИВО), полученное на предыдущей итерации [15].

Остановимся несколько подробнее на составе, структуре и вариантах функционирования данного программного комплекса (ПК).

ПРОГРАММНЫЙ КОМПЛЕКС РЕШЕНИЯ ЗАДАЧИ ПЛАНИРОВАНИЯ ФУНКЦИОНИРОВАНИЯ КФС

Программный комплекс разработан с использованием языка программирования С++.

Объекто-ориентированная спецификация программного комплекса

На этапе проектирования прототипа программного комплекса была составлена его объектноориентированная спецификация (рис. 1).

В состав программного комплекса входят следующие модули.

• •    Модуль реализации вычислительных алгоритмов . Исполняет все вычислительные процедуры. На этапе расчета необходимые значения векторов и ограничений передаются в Matlab 2012 для проведения вычислений. Результаты принимаются в указанном модуле для дальнейшего использования в расчетах.

• •    Модуль пользовательского интерфейса визуализации результатов . Предоставляет синтезированный план в виде интуитивно понятных для пользователя таблицы и графиков.

• •    Модуль пользовательского интерфейса редактора модели . Необходим для управления исходными данными и ввода параметров системы и модернизируемых информационных ресурсов.

  Модуль пользовательского интерфейса редактора модели

  
  

  Модуль пользовательского интерфейса визуализации результата

  
  

  Модуль управления параметрами модели

  
  
  

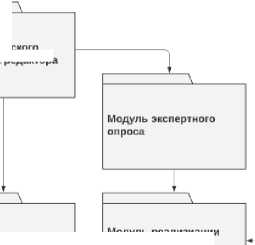
  Модуль реализиации вычислительных алгоритмов

  
  

  Модуль реализиации эвристических алгоритмов

  
  

  Модуль реализиации динамического многокритериального планирования модернизации

  
  

  Модуль взаимодействия с базой данных

  
  

  Рис. 1. Блок-схема эвристического и оптимального планирования измерительно-вычислительных операций, выполняемых КФС

  
  

• •    Модуль экспертного опроса . Является вспомогательным. В модуль встроена процедура обращения к специальному web-сервису, который возвращает значения констант λ i . Процедура опроса экспертов происходит на соответствующем web-ресурсе.

• •    Модуль взаимодействия с базой данных . В модуле реализовано преобразование из внутренних структур данных программы в структуры, хранимые в базе данных. Используется база данных SQLite.

АНАЛИЗ РЕЗУЛЬТАТОВ РЕШЕНИЯ ПЛАНИРОВАНИЯ ИЗМЕРИТЕЛЬНОВЫЧИСЛИТЕЛЬНЫХ ОПЕРАЦИЙ В КФС

Ниже излагаются экспериментальные результаты решения модельной задачи. В экспериментах измеряется текущая дальность от КФС до ОбО.

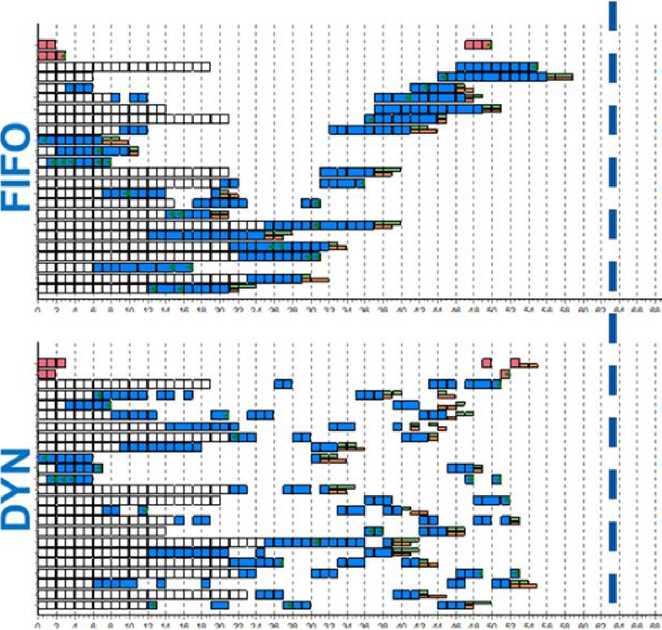
Поиск комплексного плана измерительновычислительных операций осуществлялся в два этапа. На первом этапе для инициализации обоб- щенной процедуры оптимизации измерительновычислительных операций синтезировался допустимый эвристический план. Для этого использовался широко известный алгоритм FIFO ("первый пришел — первым обслуживается"). На втором этапе реализовалась многоэтапная процедура решения двухточечной краевой задачи, к которой была сведена исходная задача неклассического вариационного исчисления. Результаты реализации данных двух этапов представлены на рис. 2.

Кроме того, были проведены дополнительные исследования процессов выполнения измерительных операций, связанные с оцениванием влияния различных факторов на указанные процессы. На представленных графиках (рис. 3, 4) видно, что для каждого ОбО с каждым новым сеансом взаимодействия с КФС повышается точность измерений параметров его положения.

Для оценивания влияния изменения различных параметров на точность измерений были проведены 2 группы экспериментов, в ходе которых изменялись коэффициенты, входящие в корреляционную матрицу ошибок, и дисперсия измерителя.

Объём необработанного информационного потока Неравномерность загруженности ресурсов Нарушение директивных сроков Обобщённый показатель качества

Объём необработанного информационного потока 11 Неравномерность загруженности ресурсов 0

Нарушение директивных сроков Обобщённый показатель качества

_j_ выигрыш 19,3%

Рис. 2. Результаты эвристического и оптимального планирования измерительно-вычислительных операций, выполняемых КФС

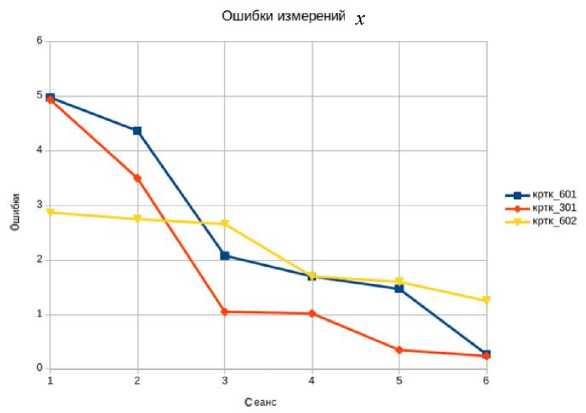
Рис. 3. График изменения ошибок измерения координат в зависимости от сеанса обслуживания для различных ОбО

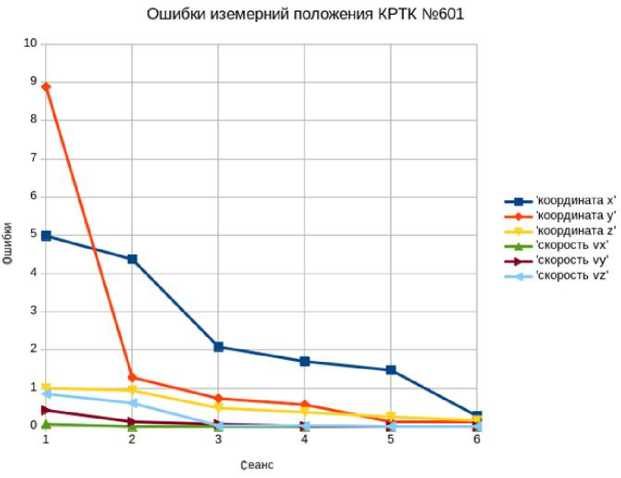
Рис. 4. Графики изменения ошибок измерений координат в зависимости от сеанса взаимодействия для выбранного ОбО

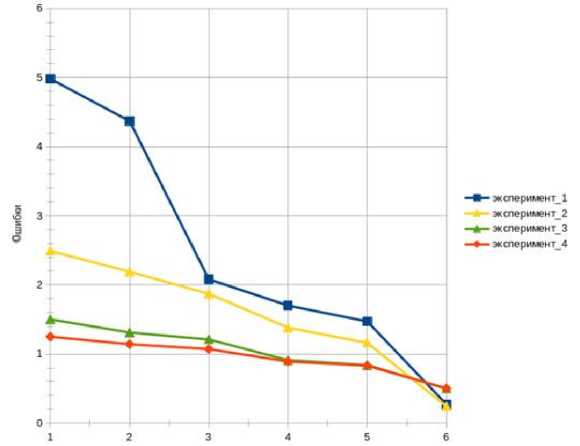
В первой группе последовательно были проведены эксперименты с изменением коэффициентов, входящих в корреляционную матрицу ошибок. В каждом из экспериментов последовательно уменьшались коэффициенты корреляции ошибок измерителя по всем измеряемым параметрам. Используемые параметры корреляционной матрицы ошибок представлены в табл. 1, а результаты экспериментов представлены на рис. 5.

Напомним, в экспериментах измеряется текущая дальность от КФС до ОбО. В таблицах и графиках приняты следующие обозначения: kx0_x, kx0_y, kx0_z, kx0_vx, kx0_vy, kx0_vz — это соответственно дисперсии ошибок оценок вектора состояния движения ОбО в трехмерном пространстве в начальный момент времени t0 (в начале интервала планирования ИВО). Компонентами вектора состояния движения ОбО являются проекции век- тора, определяющего текущее положение центра масс ОбО — x, y, z, а также проекции вектора скорости данного объекта — vx, vy, vz в абсолютной геоцентрической системе отсчета. Величины kxf_x, kxf_y, kxf_z, kxf_vx, kxf_vy, kxf_vz — это соответственно дисперсии ошибок оценок вектора состояния движения ОбО в трехмерном пространстве в конечный момент времени tf (в конце интервала планирования ИВО).

Во всех последующих таблицах приняты следующие сокращения: t _b_pl ( t _b_opt) — время начала сеанса измерений для эвристического (оптимального) плана; t _e_pl ( t _e_opt) — время окончания сеанса измерений для эвристического (оптимального) плана; x_dost — дисперсия ошибок измерителя (предполагается, что измеряется текущая дальность от КФС до ОбО).

Табл. 1. Входные параметры экспериментов с изменением корреляционной матрицы ошибок измерителя

№	kx0_ x	kxf_ x	kx0_ y	kxf_ y	kx0_ z	kxf_ z	kx0_ vx	kxf_ vx	kx0_ vy	kxf_ vy	kx0_ vz	kxf_ vz
1	5	2	10	4	1	1	1	0.36	2	0.3	0.3	0.87
2	4	2.15	1.5	1	0.75	0.55	0.65	0.39	0.41	0.28	0.12	1.22
3	2.5	1	5	2	0.5	0.5	0.5	0.18	1	0.15	0.15	0.43
4	1.25	0.5	2.5	1	0.25	0.25	0.25	0.09	0.5	0.08	0.08	0.22

Ошибки измерения координаты x

Сеанс

Рис. 5. Графики результатов проведенных экспериментов, в ходе которых проводилось изменение коэффициентов в корреляционной матрице ошибок измерителя (группа 1 экспериментов)

В качестве примера приведем полученные результаты для первого эксперимента (табл. 2). Таблицы с результатами 2–4-го экспериментов группы 1 приведены в Приложении).

Графики на рис. 5 показывают, что уменьшение коэффициентов в корреляционной матрице ошибок измерителя приводит к улучшению качества измерений. При этом из приведенных результирующих данных также видны результаты проводимого планирования измерений. Из результатов видно, что после оптимизации получаемый объем измерительной информации достигается за меньшее время. Также стоит заметить, что при наибольших значениях в корреляционной матрице ошибок измерителя в результате оптимизации наблюдается наибольшее улучшение качества измерений.

Во второй группе экспериментов последовательно уменьшались вдвое параметры дисперсии измерителя (см. табл. 3, рис. 6). В табличном виде результаты 2-й группы представлены в Приложении. Как видно из графиков рис. 5, 6, влияние параметров дисперсии измерителя в меньшей степени влияет на результаты оптимизации измерений.

Во всех экспериментах наблюдается одинаковая закономерность улучшения качества измерений с каждым новым сеансом взаимодействия ОбО с КФС.

Табл. 2. Результаты планируемых измерений для 1-го эксперимента группы 1

Станция	Сеанс	t _b_pl	t _e_pl	t _b_opt	t _e_opt	x_dost
1	3	00:16:01	00:32:00	00:16:01	00:32:00	4.98
1	4	00:40:01	00:56:00	00:40:01	00:56:00	4.37
2	6	01:52:01	02:08:00	01:52:01	02:08:00	2.08
3	4	03:36:01	03:52:00	03:36:01	03:52:00	1.7
3	1	04:00:01	04:16:00	04:00:01	04:16:00	1.47
4	2	05:20:01	05:36:00	05:20:01	05:36:00	0.27

Табл. 3. Входные параметры экспериментов с изменением дисперсии измерителя

№ эксперимента	σ измерителя
1	0.1
2	0.05
3	0.03
4	0.2

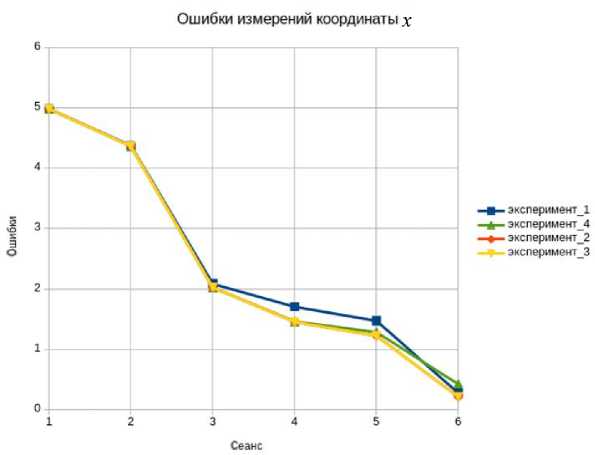
Рис. 6. График результатов проведенных экспериментов, в ходе которых изменялись параметры дисперсии измерителя КФС

ЗАКЛЮЧЕНИЕ

Представленные динамическое описание и результаты решения задачи планирования ИВО КФС дают возможность параллельного решения всего спектра задач, возникающих в процессе реализации операций технологического цикла (ТЦУ) КФС. Преимущество предложенного комбинированного метода, включающего: принципы динамического описания; опоры на результаты, полученные в современной теории управления; интеграцию фильтра Калмана; процедуру многокритериальной автоматизированной оценки разрабатываемых планов, — заключается в возможности динамического автоматизированного учета при планировании функционирования КФС различных типов ограничений, мнений экспертов и разнообразных возмущающих воздействий, влияющих на устойчивость построенных планов.

Основная особенность и отличие предлагаемых моделей заключается в логико-динамической интерпретации процессов выполнения ИВО, входящих в технологический цикл (ТЦУ) КФС. Подход позволяет существенно сократить размерности решаемых задач планирования совместного функционирования и ОбО КФС за счет динамического учета ограничений. Размерность определяется текущим фронтом работ (операций), а также заданными в каждый момент времени пространственновременными, техническими и технологическими ограничениями. Отметим, что традиционно задачи данного класса (задачи теории расписаний) решались с использованием методов математического программирования [16, 17]. Исследования результатов показали, что рациональная программа планирования функционирования КФС повышает пропускную способность КФС в целом; снижет затраты ресурсов КФС на выполнение ИВО, а также уменьшает количество запаздываний в контурах управления КФС; уменьшается возможность возникновения пиковых информационных нагрузок в различных условиях обстановки.

Подобный подход позволяет в явном виде связать технологию управления его элементами и подсистемами с результатами целевого применения приборных комплексов, осуществляющих прием, обработку и анализ данных об ООкС, а также с характеристиками аппаратно-программных комплексов КФС. Следует отметить высокую степень связности и глубинную интеграцию математических моделей в рамках единого комбинированного алгоритма планирования.

Планирование ИВО открывает перспективы формирования обоснованных требований к характеристикам аппаратно-программного комплекса КФС, например к параметрам создаваемого ими навигационного поля. На сайте [18] представлена информация о многочисленных практических реализациях предложенного подхода к решению задач теории расписаний, возникающих в различных предметных областях (космонавтика, судостроение, государственное управление и т.п.).

Исследования, выполненные по данной тематике, проводились при частичной финансовой поддержке грантов РФФИ (№№ 17-29-07073-офи-м, 18-07-01272,

18-08-01505, 19-08-00989, 20-08-01046), в рамках бюджетной темы №0073-2019-0004.

ПРИЛОЖЕНИЕ

Результаты 1-й группы экспериментов

Табл. П1. Результаты планируемых измерений для 2-го эксперимента

Станция	Сеанс	t _b_pl	t _e_pl	t _b_opt	t _e_opt	x_dost
1	3	00:16:01	00:32:00	00:16:01	00:32:00	1.5
1	4	00:40:01	00:56:00	00:16:01	00:56:00	1.31
2	6	01:52:01	02:08:00	00:40:01	02:08:00	1.21
3	4	03:36:01	03:52:00	05:20:01	03:44:00	0.91
3	1	04:00:01	04:16:00	03:36:01	04:16:00	0.84
4	2	05:20:01	05:36:00	01:52:01	05:28:00	0.5

Табл. П2. Результаты планируемых измерений для 3-го эксперимента

Станция	Сеанс	t _b_pl	t _e_pl	t _b_opt	t _e_opt	x_dost
1	3	00:16:01	00:32:00	00:16:01	00:32:00	2.49
1	4	00:40:01	00:56:00	00:40:01	00:56:00	2.19
2	6	01:52:01	02:08:00	01:52:01	02:08:00	1.87
3	4	03:36:01	03:52:00	03:36:01	03:52:00	1.38
3	1	04:00:01	04:16:00	04:00:01	04:16:00	1.16
4	2	05:20:01	05:36:00	05:20:01	05:36:00	0.24
Табл. П3. Результаты планируемых измерений для 4-го эксперимента
Станция	Сеанс	t _b_pl	t _e_pl	t _b_opt	t _e_opt	x_dost
1	3	00:16:01	00:32:00	00:16:01	00:32:00	1.25
1	4	00:40:01	00:56:00	00:40:01	00:56:00	1.14
2	6	01:52:01	02:08:00	01:52:01	02:08:00	1.07
3	4	03:36:01	03:52:00	03:36:01	03:44:00	0.89
3	1	04:00:01	04:16:00	04:00:01	04:16:00	0.83
4	2	05:20:01	05:36:00	05:20:01	05:28:00	0.5

Результаты 2-й группы экспериментов

Табл. П4. Результаты планируемых измерений для 1-го эксперимента

Станция	Сеанс	t _b_pl	t _e_pl	t _b_opt	t _e_opt	x_dost
1	3	00:16:01	00:32:00	00:16:01	00:32:00	4.98
1	4	00:40:01	00:56:00	00:40:01	00:56:00	4.37
2	6	01:52:01	02:08:00	01:52:01	02:08:00	2.08
3	4	03:36:01	03:52:00	03:36:01	03:52:00	1.7
3	1	04:00:01	04:16:00	04:00:01	04:16:00	1.47
4	2	05:20:01	05:36:00	05:20:01	05:36:00	0.27

Табл. П5. Результаты планируемых измерений для 2-го эксперимента

Станция	Сеанс	t _b_pl	t _e_pl	t _b_opt	t_e_opt	x_dost
1	3	00:16:01	00:32:00	00:16:01	00:30:00	4.98
1	4	00:40:01	00:56:00	00:40:01	00:49:00	4.36
2	6	01:52:01	02:08:00	01:52:01	02:03:00	2.02
3	4	03:36:01	03:52:00	03:36:01	03:50:00	1.45
3	1	04:00:01	04:16:00	04:00:01	04:14:00	1.22
4	2	05:20:01	05:36:00	05:20:01	05:32:00	0.21

Табл. П6. Результаты планируемых измерений для 3-го эксперимента

Станция	Сеанс	t _b_pl	t _e_pl	t _b_opt	t _e_opt	x_dost
1	3	00:16:01	00:32:00	00:16:01	00:32:00	4.98
1	4	00:40:01	00:56:00	00:40:01	00:56:00	4.36
2	6	01:52:01	02:08:00	01:52:01	02:06:00	2.00
3	4	03:36:01	03:52:00	03:36:01	03:49:00	1.43
3	1	04:00:01	04:16:00	04:00:01	04:12:00	0.19
4	2	05:20:01	05:36:00	05:20:01	05:34:00	0.21

Табл. П7. Результаты планируемых измерений для 4-го эксперимента

Станция	Сеанс	t _b_pl	t _e_pl	t _b_opt	t _e_opt	x_dost
1	3	00:16:01	00:32:00	00:16:01	00:32:00	4.98
1	4	00:40:01	00:56:00	00:40:01	00:56:00	4.36
2	6	01:52:01	02:08:00	01:52:01	02:08:00	2.02
3	4	03:36:01	03:52:00	03:36:01	03:44:00	1.46
3	1	04:00:01	04:16:00	04:00:01	04:14:00	1.28
4	2	05:20:01	05:36:00	05:20:01	05:35:00	0.42