Современные процедуры вычисления аномалий силы тяжести при высокоточных гравиметрических наблюдениях

В гравиразведке основными исходными данными для получения информации о геологическом строении территорий являются аномалии силы тяжести в редукции Буге. Очевидно, что они должны быть свободны от всех помех негеологического характера. Процедуры редуцирования стандартизированы и обязательны для всех организаций, проводящих гравиметрические работы.

Напомним основную формулу вычисления аномалий силы тяжести в редукции Буге (AgB) [2, 7]:

Agb — gna6n " У 0 + ^Фая “ <^пр.сл + ^рф, (1)

где §набл - наблюденное значение силы тяжести в гравиметрическом пункте на высоте Н', уо - нормальное значение силы тяжести; Ago_aa = 0.30867/ - поправка за свободный воздух (Фая); ^_пр.сл = 0,0419сгЯ - поправка за промежуточный слой с плотностью а, Sgpф - поправка за влияние окружающего рельефа. Принятые вычисления аномалий Буге, описанные в учебниках по геофизике и вошедшие в Инструкцию по гравиразведке [5], формализовались в 1920-1930-х гг. Параметры формул вычисления аномалий силы тяжести опирались на известные в то время сведения о форме Земли, абсолютном значении силы тяжести и минимизировали вычислительные затраты. Несмот-

ря на допущения и упрощения, эти процедуры с минимальным изменением продолжают использоваться и поныне для решения большого круга геологогеофизических задач.

В настоящее время произошли принципиальные изменения в аппаратурном оснащении гравиметрических исследований. Если ранее при работе с отечественными гравиметрами ГНУ-КВ и оптическими нивелирами среднеквадратическая погрешность определения аномалий Буге составляла +0.06-0.10 мГал, то с современными гравиметрами, системой GPS и электронными тахеометрами погрешность составляет ±0.02-0.04 мГал при точности определения наблюденных значений силы тяжести +0.005-0.015 мГал [1]. Существенным образом возросли наши знания о форме Земли, создана мировая опорная гравиметрическая сеть, в открытом доступе имеются детальные базы данных о фигуре геоида и рельефе Земли и, учитывая современные вычислительные мощности, нет никаких причин для применения упрощенных формул при вычислении поправок и редукций в гравиметрические наблюдения.

Рассмотрим основные допущения процедур редуцирования, принятых при обработке полевых гравиметрических данных.

Система высот

Высоты гравиметрических пунктов определяются в России в Балтийской системе высот, т.е. как превышение относительно поверхности геоида или уровня моря (Н), в то время как нормальное поле определяется на уровенном эллипсоиде на высоте h (рис. 1). Разница между этими высотами N = h - Н называется ундуляци-ей геоида. Поскольку пункты с измеренными и нормальными значениями относятся к разным поверхностям, то вычисленные аномалии называются смешанными [7]. Поправка за высоту N называется косвенным эффектом.

В настоящее время благодаря спутниковым наблюдениям и обобщению наземных, морских и аэрогравиметрических съемок ундуляции геоида определены с достаточно высокой точностью. Кроме того, применение систем спутниковой навигации GPS и ГЛОНАС позволяет определять превышения пунктов наблюдений относительно базовой станции в геодезической системе высот. Использование эллипсоидальных высот автоматически снимает вопрос о необходимости учета косвенного эффекта.

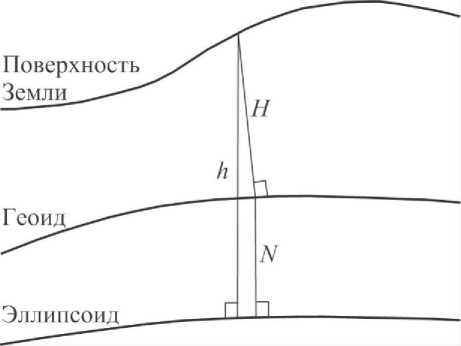
Рис. 1. Схема соотношения между системами высот

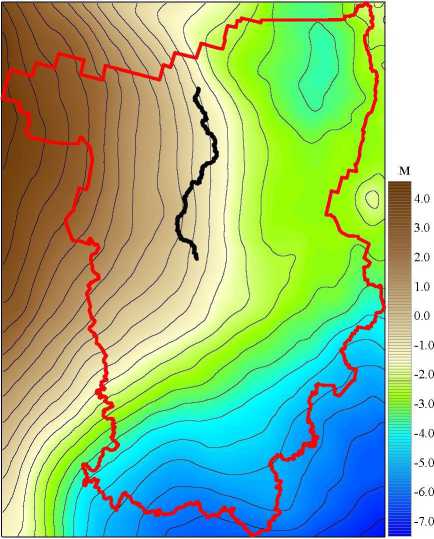
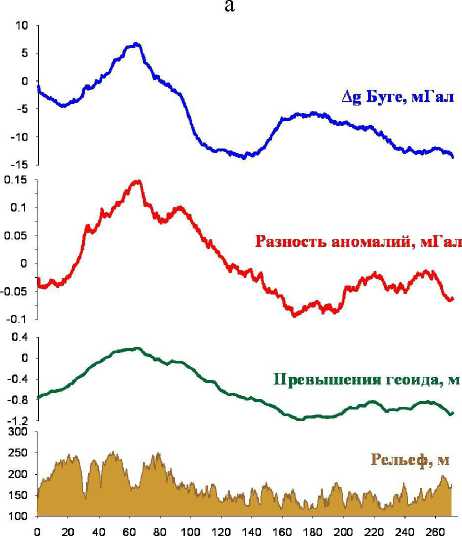
На рис. 2 представлены разности аномалий в свободном воздухе, вычисленные с высотами относительно геоида и эллипсоида, для регионального профиля на севере Пермского края. Среднеквадратическая погрешность определения наблюденных значений силы тяжести на данной площади составила ±0.017 мГал; высот -±0.10 м. Ундуляции геоида вдоль профиля составляют более 1 м (рис.2, а). Разность аномалий Буге, вычисленных с высотами относительно геоида и относительно эллипсоида (рис.2, б), достигает 0.15 мГал, т.е. практически на порядок превышает точность съемки.

Нормальное значение силы тяжести

Нормальное значение силы тяжести на поверхности уровенного эллипсоида вы- числяется по формуле А.Клеро, которая с членами второго порядка записывается следующим образом [8]:

/о = Ze (1 + /3 sin²^ - ^1 sin²2^), (2)

б

Рис. 2. Разность поправок в свободном возду хе, вычисленных с высотами относительно геоида и эллипсоида: а)ундуляции геоидана территории Пермского края (черной линией показан гравиметрический профиль): б) графики аномалий по профилю где /3=(ур- /ф/ус, /31 = а2/8 + а/3/4, а = (а-Ь)/а, /р и /е - нормальные значения силы тяжести на полюсе и экваторе эллипсоида, а м Ъ - соответственно большая и малая полуоси эллипсоида, (р - широта.

Инструкция по гравиразведке [5] предписывает вычислять нормальное значение силы тяжести по формуле Ф.Р.Гельмерта, которая выведена им в 1909 г. по 1603 наблюдениям силы тяжести [3]:

/о = 978030 (1 + 0.005302 sin2^ - (3) 0.000007 sin22^).

После Гельмерта определением постоянных формулы (2) занимались многие ученые (Кассинис, 1930; Жонголович, 1952; Moritz, 1980 и др.). В настоящее время в России Распоряжением Правительства РФ от 28.12.2012 г. №1463 установлены единые государственные системы координат (ПЗ-90.11 - «Параметры Земли 1990 года»). Подставляя в (2) значения ПЗ-90.11, получим

/0 = 978032.84 (1 +0.0053024 sin2^ - (4) 0.0000058 sin22^).

Сравнение значений нормального поля, вычисленных по формуле Гельмерта с параметрами ПЗ-90.11 (рис. 3), показывает, что для крупномасштабных гравиметрических съемок нет принципиальной разницы, какую из формул использовать при вычислении аномалий силы тяжести. Для средних широт градиент разности значений нормального поля, вычисленный по различным формулам, составляет около 0.05 мГал на 1 градус (т.е. примерно на 100 км) и легко может быть исключен из гравитационного поля как часть регионального фона. Однако при региональных гравиметрических съемках и составлении сводных гравиметрических карт использование формулы Гельмерта приведет к существенным искажениям поля.

Вертикальный градиент силы тяжести

Поправка за высоту (редукция Фая или «в свободном воздухе»), по сути, представ- ляет собой нормальный вертикальный силы тяжести к пункту наблюдений на градиент силы тяжести. Она предназначе- поверхности Земли.

на для приведения нормальных значений

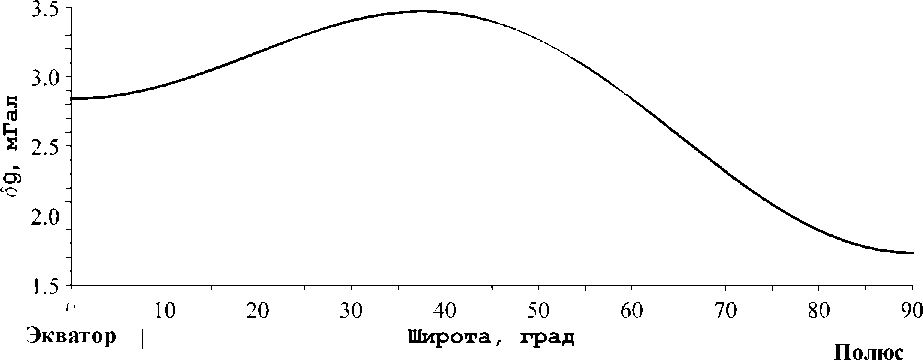
Рис.З. Разность значений нормального поля, вычисленныхпо формулеГелъмерта с параметрами ПЗ-90.11

В практике гравиразведки [2, 5], предполагая, что Земля является шаром с радиусом 6371 км и значением нормального поля 980 Гал, используется формула dgh = 0,3086Я. (5)

Аналитическое выражение вертикального градиента силы тяжести для эллипсоида приведено в отечественной и зарубежной литературе [11, 8]. Линейный (c'y ch) и квадратичный (с?у А п) коэффициенты вертикального градиента нормального поля силы тяжести по нормали к поверхности эллипсоида п вычисляются по формулам [8]

дп а

1+a-q- \Ъа - -q^sin^ (р t2y = 3уе

2 ’ д п а

где у_е - значение силы тяжести на экваторе, а - большая полуось общего земного эллипсоида, а - полярное сжатие эллипсоида, q = со² а! у., со - угловая скорость вращения Земли. Обычно формула поправки за высоту пункта наблюдения приводится к виду

3gh = (Ад + k₂sm²(p)h + k₃h² . (7)

Подставляя в формулы (6) и (7) значения ПЗ-90.11, получим

8g_h = - (0.3087727654 -                  (8)

0.0004308698sin2^)A + 7.21252х 1O'SA2 .

На рис. 4 приведен график разности поправок в свободном воздухе по формулам (5) и (8) для широт, на которых расположен Пермский край. Как видно из графика, неучёт эллипсоидальности Земли для данного региона приводит к перекосу поля более чем на 0,4 мГал.

Поправка за промежуточный слой

При введении этой поправки предполагается, что промежуточный слой представляет собой плоскопараллельную горизонтальную пластину с постоянной плотностью 2,30 г/см3, 2,67 г/см3 или некоторой средней для конкретной площади исследований. Влияние отклонений физической поверхности Земли от плоскости учитывается введением специальной поправки - поправки за влияние рельефа.

Притяжение плоского однородного слоя толщиной Н и плотностью а вычисляется по формуле [2]

где f - гравитационная постоянная, официальное значение которой, даваемое международной комиссией по константам, составляет

(6.67259±0.00085)10-ⁿ mW.

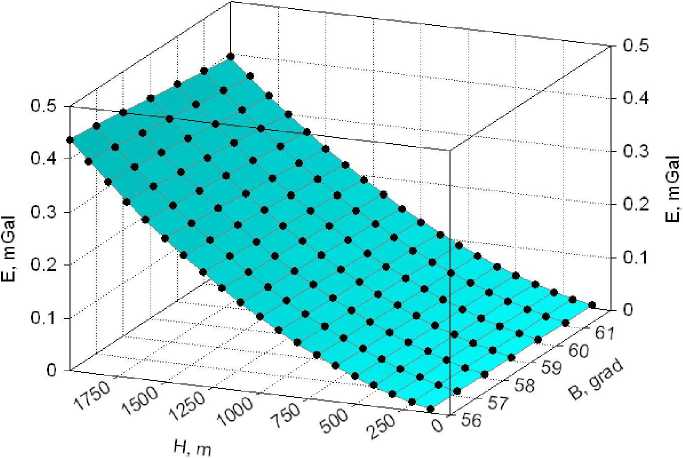
Рис. 4. Зависимости погрешности поправки в свободном воздухе от широты и в ысоты пункта наблюдения

Формулу вычисления притяжения сферического сегмента вывели В.М. Гордин, Г.Г. Ремпель, А.И. Каленицкий и В.П. Смирнов. T.R. LaFehr [10] привел ее к простому виду

^сф.ел = 2л/а(рН- AR), (10) где р= (1/3 т/2 - г/), л ф

-С^к + диЬп---

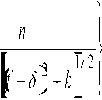
5 = RCR, r/ = h/R, d=3cos2a-2, f=cosa, k = sin2a, p = -6cos2a sin(a/2) + 4sin3(a/2), m = -3sin2a cosa, w = 2[sin(a/2) -sin2(a/2)], R = Ro + H, a = S/Ro, S - радиус сферического сегмента a Ro - радиус Земли (рис. 5).

Сравнение формул (9) и (10) при S = 166,735 км показывает весьма большое расхождение между величинами поправок (рис. 6).

пункт наблюдения

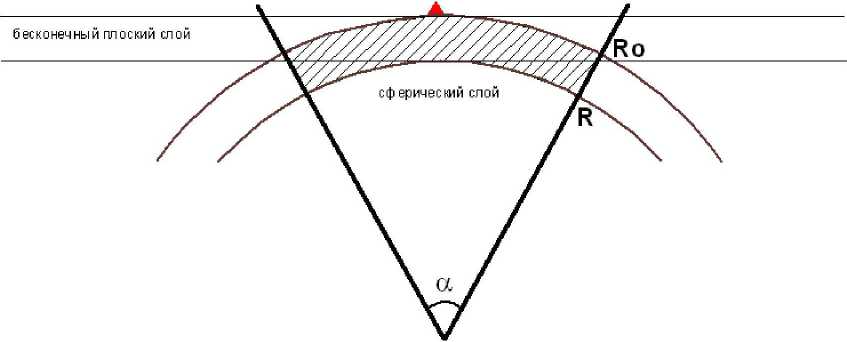
Рис. 5. Сферический и плоский слои Буге

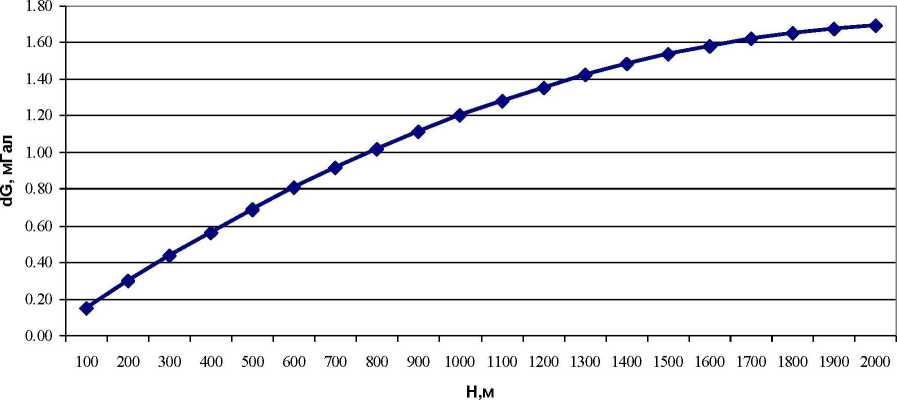
Рис. 6. Разность поправок Буге для плоской и сферической Земли в зависимости от в ысоты

Поправка за влияние рельефа

Вычислением поправок за влияние рельефа с учетом кривизны Земли занимался П.И. Лукавченко [6]. Им предложены простые формулы учета превышений не только относительно высоты геоида, но и относительно горизонтальной плоскости, проходящей через гравиметрический пункт (рис. 7):

^РФ® = ^рф(^) - ^рф(^ для Я < Л,

^рф(^) = ^рф(^) - ^рф(^)     ’ для Н > h,

%рФ® = ^рф(^+^) - ^рф(^) для Н < 0.

Следует отметить, что если при «плоской» Земле все поправки за влияние рельефа положительны, то при учете сферичности они знакопеременны. Вычитать следует влияние масс пород, слагающих рельеф, лежащих ниже горизонтальной плоскости, проходящей через гравиметрический пункт и выше поверхности земного эллипсоида относительно высоты пункта (рис. 7).

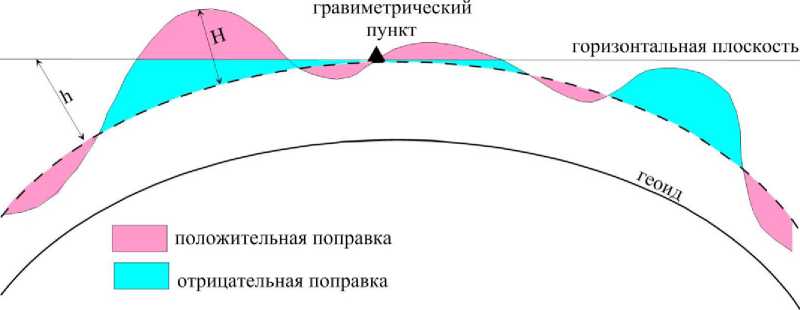
Рис. 7. Вычисление поправок за влияние рельефа с учетом сферичности Земли

Использование формул (11) позволяет нологии, разработанные для «плоской» применять для вычисления поправок тех- Земли [4], вычисляя расстояния до призм, аппроксимирующих рельеф, в соответствии с углом наклона поверхности Земли.

Поправка за влияние атмосферы

Масса атмосферы Земли включена вместе с массой твердой Земли в нормальное значение силы тяжести на поверхности уровенного эллипсоида (4). Однако масса атмосферы выше гравиметрического пункта не воздействует на измеренное значение силы тяжести, предполагая однородный состав атмосферы сферических оболочек. Гравитационный потенциал однородной оболочки в любой точке в её пределах постоянен, таким образом, величина силы тяжести от перекрывающей оболочки равна нулю. Следовательно, влияние атмосферных масс Baffin мГал 0.8--'

Об ол—

0.2 —

формула (12)

формула (13)

необходимо исключить из аномалий силы тяжести, т.е. вычесть из нормального значения силы тяжести.

Согласно ПЗ-90.11 поправка в ускорение нормальной силы тяжести за притяжение атмосферы на уровне моря равна 0.87 мГал. На высоте Н ее предлагается вычислять по формуле

Ат = 0 87^“°- 116я1°47

д£атм о.о/е . (12)

В зарубежной литературе [8] предлагается использовать следующее аналитическое выражение:

3g_amM = 0.874 - 9.9x10^+3.56x10^, (13)

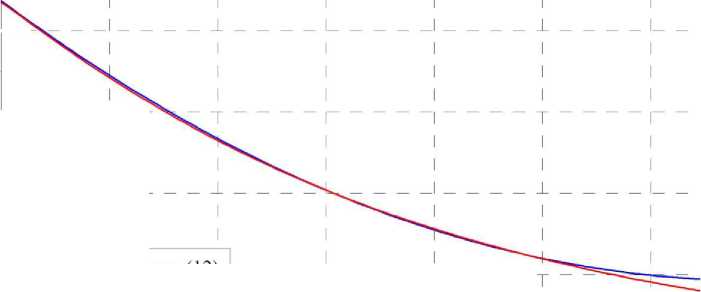
Сравнение формул (12) и (13) показывает, что до высоты 8 км разность значений поправок не превышает 0.006 мГал (рис. 8), поэтому нет принципиальной разницы, какую из формул использовать.

0           2           4           6           8           10          12 Я,км

Рис.8. Сравнение формул вычисления поправки за влияние атмосферы

Эта поправка особенно необходима при гравиметрических съемках, проводимых в районах с большим перепадом высот. Следует отметить, что формула (4) не учитывает вариации атмосферного давления.

Программное обеспечение

Для вычисления аномалий силы тяжести в редукции Буге с использованием различных формул редуцирования разработана программа, интерфейс которой приведен на рис. 9. Программа позволяет вычислять аномалии Буге по стандартным формулам, которые определены Инструкцией по гравиразведке [5], и по формулам, выведенным в разное время различными исследователями. В программу заложены параметры принятого в России земного эллипсоида, современные данные о геоиде и рельефе Земли.

Для определения средней плотности промежуточного слоя по формулам (9) или (10) в программу включен блок, который, используя метод Неттлетона [2], вычисляет коэффициенты корреляции между аномалиями Буге и рельефом.

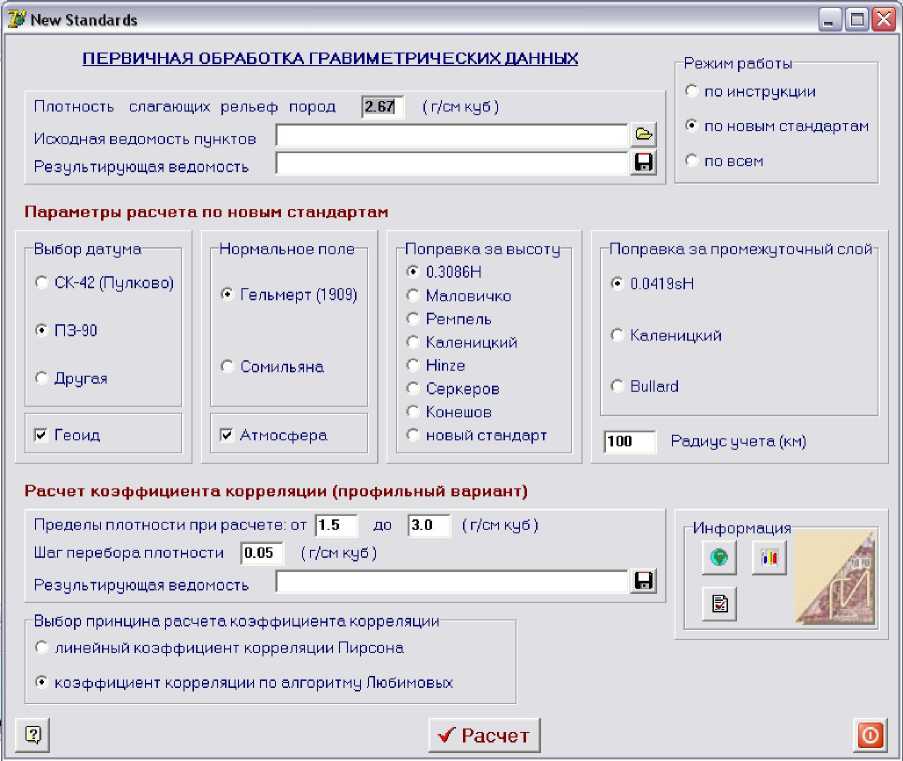
Рис. 9. Интерфейс программы вычисления аномалий Буге по различным формулам

Пример вычисления аномалий силы тяжести

Рассмотрим пример вычисления аномалий силы тяжести на одном из участков гравиметрической съемки на востоке Пермского края (рис. 10). Размеры площади примерно 18x27 км; перепад высот рельефа от 140 до 500 м. Измерения проведены высокоточными гравиметрами Autograv CG-5 с привязкой гравиметрических пунктов с помощью спутниковой системы GPS-Глонасс Trimble-R8 и электронных тахеометров. Среднеквадратическая погрешность определения наблюденных значений силы тяжести на данной площади составила +0.033 мГал. Обработка полевых гравиметрических данных выполнена двумя способами: по формуле (1) и с использованием описанных выше процедур редуцирования, основанных на международно принятых уравнениях и параметрах. Кроме того, во втором случае использовались высоты гравиметрических пунктов относительно референц-эллипсоида.

Как видно из рисунка, разность аномалий, вычисленных различным способом, достигает ±0.10 мГал, т.е. в три раза превосходит точность полевой съемки. Разность аномалий возникает, в основном, за счет ошибки использования упрощенной формулы вычисления аномалий в свободном воздухе и пренебрежения влиянием атмосферного эффекта. Погрешность, обусловленная использованием различной системы высот (косвенный эффект), практически не сказывается на морфологии локальных аномалий из-за небольших размеров площади съемки.

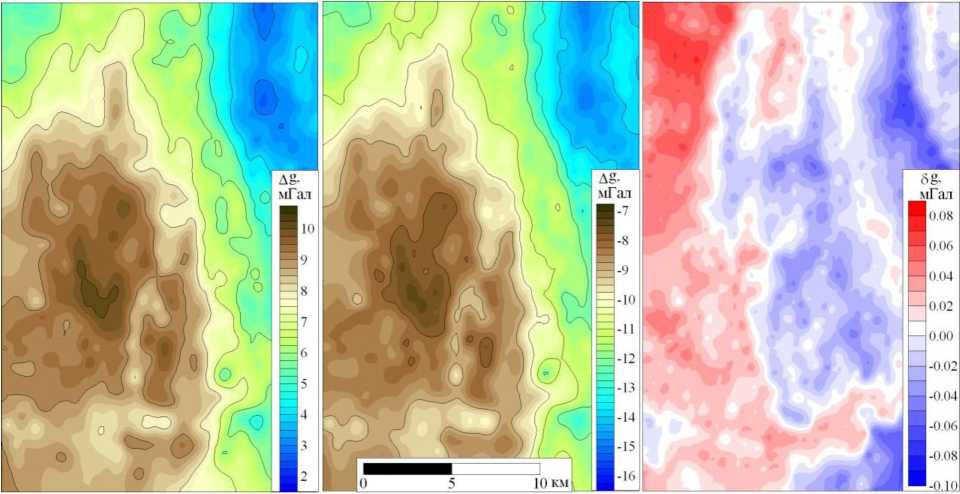
Рис. 10. Сравнение аномалий Буге, вычисленных различным способом: а) принятым в России: б) по предлагаем ъш формулам: в)разность аномалий

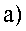
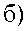
Заключение

Возможности гравиразведки на современном этапе вступают в противоречие с существующими инструктивными требованиями к ее проведению. Несомненно, что использование современной формулы вычисления нормального поля, а не выведенной Ф.Р.Гельмертом в 1909 г., учетэл-липсоидальности Земли при определении вертикального градиента и промежуточ-