Современные возможности и применение беспилотных летательных аппаратов: изучение и возможности усовершенствования трехмерной гистограммы векторного поля для обхода препятствий

Беспилотные летательные аппараты используются для решения самых разных практических задач. Например, они могут следить за состоянием сельскохозяйственных полей, осуществляя регулярную аэрофотосъемку или распыляя удобрения на заданных участках местности.

В свою очередь, для автономного управления дрону необходимо как минимум знать с высокой точностью свои координаты в пространстве. На открытом пространстве можно использовать GPS – точность достигается в несколько метров. Обычного GPS хватает для создания маршрута полета на открытой местности. Но для детального исследования, например строящихся объектов или полетов в дикой природе, применяются узкоспециализированные алгоритмы.

Первоначальная модификация VFH

Рассмотрим более подробно базовую модификацию гистограммы векторного поля [1], на основе которого строятся все дальнейшие улучшения. В методе VFH , существует три уровня представления данных:

• 1.    Самый высокий уровень содержит подробное описание окружения робота. На этом уровне двумерная декартова сетка гистограммы постоянно обновляется в режиме реального времени получая данные от встроенных датчиков дальности о расстоянии до препятствия.

• 2.    На промежуточном уровне вокруг текущего местоположения робота строится одномерная полярная гистограмма. Она состоит из n угловых секторов шириной a .

• 3.    Нижний уровень представления данных – это выходные данные алгоритма VFH : эталонные значения для контроллеров привода и рулевого управления транспортного средства.

На первом этапе обработки данных активная область сетки гистограммы отображается на полярной гистограмме как изображено на рисунке 1. Содержимое каждой активной ячейки в сетке гистограммы теперь рассматривается как вектор препятствия, направление которого определяется направлением Р от ячейки к центральной точке мобильного робота.

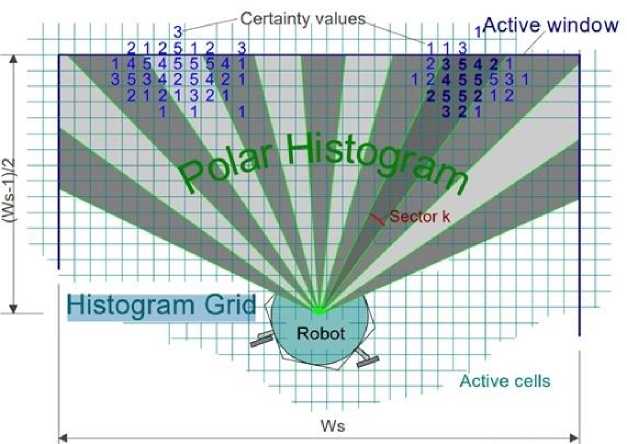
Рис. 1. Гистограмма векторного поля ( VFH)

Направление вектора P и величина вектора препятствия в ячейке тц вычисляются по формулам:

&у = tan-1^^;                      (1)

^i,j              % ! — X q

mi,j = (cij)4a - bdijh                    (2)

где a, b – положительные константы; C i,j - значение достоверности активной ячейки ( i, j ); dij - расстояние между активной ячейкой ( i, j ) и центральной точкой мобильного робота; тц - величина вектора препятствия в ячейке ( i, j ); х₀, y₀ - текущие координаты мобильного робота; X i ,y j - координаты активной ячейки ( i, j ); P ij - направление от активной ячейки ( i, j ) к точке мобильного робота.

Улучшенная модификация 3 DVFH

Рассмотрим подробно математическую модель алгоритма трехмерной гистограммы векторного поля 3 DVFH , созданного на основе его первоначальной версии VFH ( Vector Field Histogram ).

До сих пор все алгоритмы VFH использовались в 2D-среде для наземных робо тов, однако, Ваннест и др. [10] разработали алгоритм 3DVFH позволяющий расширить область зрения до трехмерной среды и применять алгоритм на летающих роботах. Этот алгоритм нельзя считать полностью локальным, поскольку он строит карту окружающей среды в виде Octomap (эффективный вероятностный каркас трехмерного картографирования на основе октодеревьев)[11].

На основе Octomap создается трехмерная карта занятости с учетом только вок-селей в ограничивающей рамке вокруг транспортного средства. Структура октодерева отображена на рисунке 2: белые листовые узлы имеют статус свободных, серые листовые узлы имеют статус занятых.

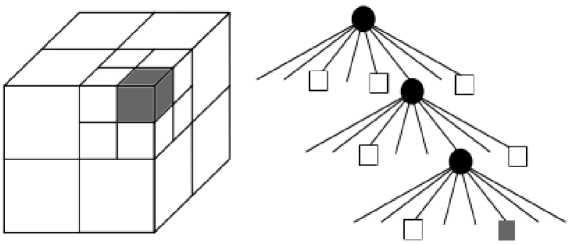
Рис. 2. Принцип построения октодеревьев

На основе трехмерной карты занятости строится двухмерная полярная гистограмма, в которой обнаруживаются и оцениваются пробелы, чтобы найти наилучшее направление для движения в трехмерной среде. Затем, исходя из этих вычислений рассчитываются потенциально опасные участки на маршруте. Полный пройденный путь из точки А в С показан на рисунке 3.

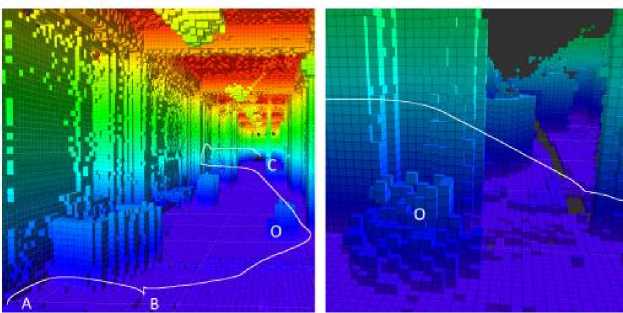
Рис. 3. Результат работы алгоритма 3DVFH

В своем исследовании Танджа Бауман и др. [19] улучшили алгоритм 3 DVFH добавив в него подход использования памяти дрона. Данный подход использует данные из последнего временного шага для улучшения гистограммы, построенной на текущем временном шаге. Однако сохраненные старые данные представлены в виде гистограммы. Старая гистограмма являет собой полярное представление препятствий, замеченных на предыдущем временном шаге. Поскольку угловое направление препятствия зависит от местоположения дрона, старая гистограмма привязана к старому местоположению, в котором она была построена. Чтобы использовать данные старой гистограммы для вычислений на текущем временном шаге, ее необходимо преобразовать в гистограмму в текущем местоположении дрона.

Это может быть достигнуто путем повторного проецирования занятых ячеек старой гистограммы в трехмерные точки и последующего построения гистограммы памяти из этих трехмерных точек. Чтобы получить повторно спроецированные точки, старая гистограмма сканируется на предмет занятых ячеек. Каждая из этих занятых ячеек характеризуется г углом возвышения и углом азимута £. В дополнение к этим углам расстояние сохраняется в слое расстояний старой гистограммы, а возраст – в слое возраста. Если возраст занятой ячейки не превышает определенный предел, ячейка повторно проецируется на четыре трехмерные точки, соответствующие углам ячеек. Углы возвышения и азимута четырех угловых точек могут быть вычислены путем добавления / вычитания половины углового разрешения α гистограммы из углов возвышения и азимута занятой ячейки:

a         ^

^£ i ^{— £} + ~, ^ i = ^ + ~,¹ = 1,4;

где £ - угол возвышения занятой ячейки; ^ i - угол азимута занятой ячейки.

Затем эти четыре точки можно повторно спроецировать в трехмерное пространство:

P ix ^— pos_{old x} + ^d cos(8 i ^ sin« i ^);

Piy— Posoiay + d cos(£i ^) cos(^i ^); Рц — Posoid^ + dsin(£i^),

где £ - угол возвышения занятой ячейки; ^ i - угол азимута занятой ячейки; рц -вычисление трехмерной точки; pos - положение дрона.

Чтобы получить гистограмму окружающей среды, сначала необходимо преобразовать трехмерные точки в двухмерную первичную полярную гистограмму, где каждая ячейка содержит количество точек, лежащих в соответствующем секторе. Для каждой трехмерной точки Pi, вычисляются угол возвышения £ и азимутальный угол ^, видимый из текущего положения pos дрона:

5 — ~ atan(2px — 2posx, 2ру — 2posy);

£ — ¹⁸⁰ atan П

p ^ -pos^.

(P x -pos_x⁾² + (p_y-pos_y)²

)

После определения углов трехмерной точки их необходимо преобразовать в индексы гистограммы. Расчетные углы находятся в диапазоне ^ 6 [-180, 180] и [-90, 90]. Сначала эти углы нужно преобразо- вать в положительные диапазоны £ 6 [0, 360] и [0, 180]. По этим положительным углам могут быть рассчитаны индексы гистограммы:

P temp ^—

Р + (a — mod(P; а));

P index ^—

S temp a

где в - положительный угол (или ^), который необходимо преобразовать; £_i -угол возвышения занятой ячейки; а - разрешение гистограммы; рц - трехмерная точка, mod(P;a) - остаток от деления Р на a

Эта процедура используется дважды в процессе получения объединенной гистограммы для навигации: для получения гистограммы памяти из повторно спроецированных точек и для вычисления новой гистограммы из облака точек, предоставленного стереокамерой. В обоих случаях первичная полярная гистограмма рассчитывается одинаково. Однако пороговые значения для преобразования в двоичную гистограмму различаются, так как общее количество точек 3D сильно различается. Также размер ячейки гистограммы памяти больше, поскольку она построена с половинным разрешением. Для новой гистограммы ячейка в двоичном слое устанавливается как занятая, если в нее попадает хотя бы одна трехмерная точка.

Алгоритм 3DVFH начинает использовать новое полное облако точек с камеры. Затем он обновляет параметры функции стоимости в соответствии с достигнутым прогрессом. Это позволяет дрону подняться, если невозможно найти дорогу для обхода препятствия. Алгоритм 3DVFH строит дерево поиска, чтобы предложить различные возможности перемещения. Это дерево имеет корень в текущей позиции беспилотного летательного аппарата. Эта позиция вводится в дерево как первая точка отсчета и устанавливается функция стоимости дерева, а также эвристика для первого узла. Оттуда новые узлы вводятся в древовидную структуру до тех пор, пока заданное количество узлов N не будет расширено (рис. 4).

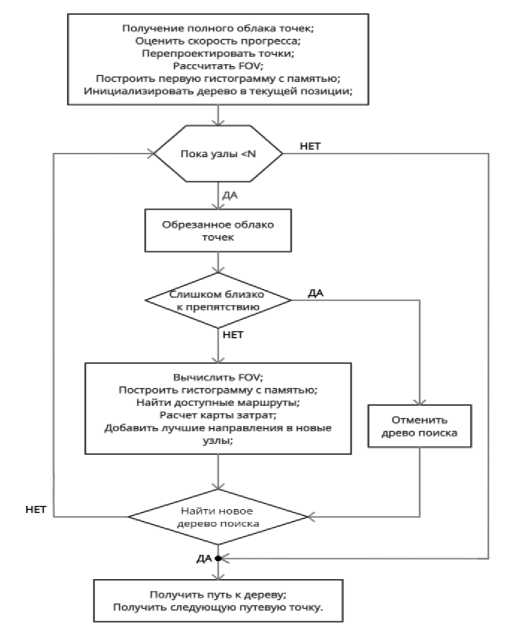
Рис. 4. Алгоритм построения гистограммы 3DVFH

Построение дерева поиска достигается путем повторения подхода гистограммы для каждой предполагаемой будущей позиции дрона. Чтобы развернуть узел, сначала обрезается все облако точек вокруг его текущего положения. Точки обрезанного облака точек будут проверяться на предмет их расстояния до дрона. Поскольку текущий узел – это всего лишь предположение о возможном движении, он не требует реакции, если он находится слишком близко к препятствию. Но если узел находится слишком близко к препятствию, его стоимость устанавливается на бесконечность. Вместо того, чтобы расширять его, дерево будет искать следующий лучший узел.

Чтобы расширить узел, рассчитывается FOV (поле зрения) в его положении. Ги- стограмма строится как комбинация гистограммы обрезанного облака точек и гистограммы повторно спроецированных точек. Чтобы объединить эти две гистограммы, необходимо поле обзора дрона в позиции узла. Гистограмма имеет пониженную дискретизацию до половины разрешения, чтобы уменьшить количество возможных направлений и сделать их более четкими. Направления-варианты извлекаются и оцениваются в соответствии с той же функцией стоимости, что и для алгоритма 3DVFH. Чтобы уменьшить фактор ветвления дерева поиска, не все варианты добавляются как узлы.

Архитектура всего алгоритма избегания препятствий со всеми функциями показана на рисунке 5.

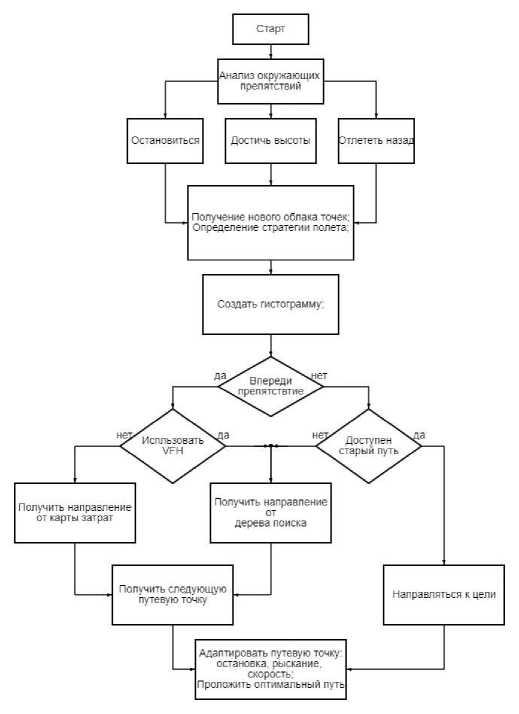
Рис. 5 . Общая структура алгоритма выбора пути

Потенциал возможного улучшения алгоритма 3 DVFH

В рассматриваемом алгоритме уклонения от препятствий показано, что введенная стратегия памяти используется, как для полетов на открытом пространстве, так и для выполнения сложных сценариев. Следовательно, эффективность алгоритма не зависит от глобальной карты среды, что снижает вычислительные затраты алгоритма.

Алгоритм гистограммы векторного поля (VFH) был расширен до трехмерной среды, а преимущества функции памяти были воспроизведены в алгоритме 3DVFH. Благодаря этой возможности упреждения алгоритм хорошо справляется в более сложных сценариях. Реализован простой в вычислительном отношении метод обнаружения земли с использованием только данных с передней камеры. Было показано, что метод наземного обнаружения может поддерживать минимальное расстояние до земли. Реализованы различные функции, чтобы повысить надежность предлагаемого подхода и сделать возможным его применение на беспилотных летательных аппаратах.

Однако алгоритм обладает недостатками. Производительность алгоритма сильно ограничена доступной информацией о датчике. Вероятность столкновения может быть уменьшена, а скорость полета могут быть увеличены за счет использования дополнительных датчиков увеличения поля зрения. Хоть алгоритм и определяет окружение почти на 360 градусов, для анализа такого пространства ему необходимо вращаться вокруг своей оси постоянно осматриваясь, на что уходит лишнее время. Дрон не может моментально рассчитать возникшее препятствие, например встречно движущегося объекта, что приведет к столкновению и потере БПЛА. Так же алгоритм тратит много времени на вычисление лучшей траектории из возможных.

Из вышеперечисленных недостатков, можно сделать вывод, что алгоритм нуждается в модификации. Поэтому существует ряд потенциальных возможностей ав- торской модификации алгоритма. Алгоритм возможно улучшить путем добавления новых ограничений к функции стоимости предварительного построения дерева пути, расширив его, чтобы включить не только положения, но и скорости. В этом случае наилучшей траекторией будет компромисс между длиной пути и скоростью.

Моделирование вероятности столкновения может быть выполнено разными способами, и в реальной жизни существуют сценарии для конкретных случаев, которые необходимо учитывать. Например, дрон с одной фронтальной камерой может счесть горизонтальное движение более безопасным, чем вертикальное. Априорная высота дает хороший способ оценить преимущества набора высоты, но это значение необходимо знать заранее. Адаптивная модель, которая оценивает, насколько сложно найти пути в текущей среде, может быть интересным расширением.

Также может быть полезен динамический поиск, в котором используется информация из предыдущего поиска и тогда сократится время анализа данных. За счет непрерывного выполнения задержка между запросом нового пути и новым решением может быть уменьшена, что позволит алгоритму находить лучшие пути еще быстрее.

Динамическая модель данного алгоритма, поможет улучшить скорость обработки информации, получаемой с датчиков. Многие задачи, решаемые динамическим программированием, можно определить как поиск в заданном ориентированном ациклическом графе кратчайшего пути от одной вершины к другой. Согласно допущениям динамической модели, угловые скорости вращения пропеллеров можно изменять моментально.

Расширение области видимости с помощью расширения обрабатываемых данных или с помощью добавления дополнительной системы машинного зрения должно увеличить порог безопасности полета дрона и радиус определения препятствий на пути.

Заключение

Анализ публикаций в области исследования позволяет сделать вывод, что методы решения уклонения от препятствий на автономном квадрокоптере, обладают потенциалом для модификации, эффективности и точности расчетов алгоритма. Учитывая вышеизложенные материалы, в дальнейшем предполагается разработать улучшенный аналог рассматриваемого алгоритма, который будет способен более качественно и с меньшей задержкой выполнять свои задачи.