Современный взгляд на геометрию реальных поверхностей деталей изделий машиностроения

Для адекватного представления о геометрии в машиностроении воспользуемся понятийно1-аксиоматическим методом. В дальнейшем изложении воспользуемся этим способом для определения состава и пояснения всех необходимых понятий. Будем приводить их в сносках, сопровождающих текст.

Термины ², представляющие идеализированные свойства исследуемых объектов и процессов, формулируют понятия в виде истин, доказанных ранее или не требующих доказательства – аксиом3 .

По строгим правилам логического вывода из них выводятся другие истинные свойства – теоремы4 .

Совокупность умозаключений5 – теория ⁶ отражает объективно существующие отношения и связи между явлениями объективной реальности в совокупности и образует однозначную детерминированную⁷ математическую модель8 исследуемого объекта, которую в дальнейшем можно представить вероятностной или стохастической⁹ моделью.

Номинальная и реальная геометрия детали

Объектами машиностроения являются физические тела. Изделия10 машиностроения представляют собой результат сборки11 совокупности деталей12, являющихся наименьшими частями машин. Геометрия деталей в машиностроении играет определяющую роль. Она пронизывает все стадии и этапы жизненного цикла изделия. Объем13 детали ограничен от окружающей среды конечным множеством поверхностей14, разной величины,15 формы16. и размеров17. Поверхность является первичным геометрическим элементом18 (точкой19, линией20, профилем поверхности21, поверхностью) конструкции детали, однозначно определёнными в системе координат22. Поверхности пересекаются или сопрягаются по рёбрам23 или линиям сопряжения24. выбранной системе координат25 их величина и расположение26 ограничивают объём тела27 деталей.

Рёбра деталей машиностроения обычно имеют скругления ²⁸ углов определённого радиуса или фаски ²⁹, представляющие собой вспомогательные поверхности . В местах пересечения более чем двух поверхностей, а также двух линий пересечения или сопряжения образуются точки пересечения. Основные поверхности деталей взаимодействуют с окружающей средой. По соприкасающимся поверхностям разных деталей осуществляется сборка деталей друг с другом.

Геометрические элементы детали могут быть:

• -    несимметричными (их больше) и симметричными с осевой или центральной симметрией (их меньше);

• -    с кривизной (их бесконечно большое количество) и без кривизны (это прямая линия и плоскость).

Замысел геометрии детали, как и всякого другого элемента конструкции, рождается в системе координат проекта ³⁰ совокупностью геометрических элементов, имеющих номинальную геометрию ³¹ , заданную в собственных системах координат ³².

Геометрию замысла называют номинальной геометрией детали ³³ . Геометрические параметры формы номинальных геометрических элементов (линий, поверхностей) зависят от способа их образования: кинематического или каркасного (линейного или точечного) с последующим двумерным интерполированием формы [1].

Реальную геометрию ³⁴ поверхностей детали получают после изготовления из заготовок ³⁵ по выбранному технологическому процессу ³⁶ с помощью выбранных средств технологического оснащения (СТО): технологического оборудования,³⁷ технологической оснастки ³⁸ , приспособлений ³⁹ и инструментов ⁴⁰ , и измеряют выбранными средствами измерения ⁴¹ .

Реальная геометрия геометрических элементов детали может быть представлена координатами точек реальной поверхности в системе координат системы измерения ⁴². Она отличается от номинальной геометрии, представленной в системе координат проекта отклонением формы и расположения реальных геометрических элементов детали от формы и расположения номинальных геометрических элементов.

Рассматривать всю деталь как целое и сравнивать геометрию реальной детали с номинальной геометрией детали можно, но неэффективно. Поскольку первичным геометрическим элементом детали является поверхность, то переход от рассмотрения геометрии детали в целом к реальным поверхностям, ограничивающим объем детали, сулит большие перспективы при решении задач оптимизации ограничений допусков ⁴³ на традиционные отклонения формы и расположения поверхностей в конструкторской и технологической документации.

Геометрические параметры формы и расположения реальных геометрических элементов (линий, поверхностей) детали, определяемые характерными размерами ⁴⁴ длин и углов, заданы в технической документации и могут быть больше или меньше только в пределах поля допуска ⁴⁵, обеспечивающего гарантированную собираемость ⁴⁶ и работоспособность ⁴⁷ машин.

Характерные размеры поверхностей деталей традиционно измеряют простейшими двухточечными48 инструментами (штангенциркуль, микрометр), оценивают по весьма приблизительным рекомендациям [2] и определяют в соответствии с несовершенными установленными правилами [3, 4, 5].

Наиболее полную и достоверную информацию о реальной геометрии детали можно получить с помощью 3D координатно-измерительных машин ⁴⁹ (КИМ). В результате измерения в системе координат системы измерения получают массивы координат точек реальных геометрических элементов деталей машин (поверхностей, линий).

По сложившейся терминологии в машиностроении для каждого реального геометрического элемента к одноимённому номинальному геометрическому [3,4].

Математическая модель определения отличия отклонений величины, расположения и формы реального элемента в системе координат системы измерения от номинальной геометрии геометрических элементов, представленных в системе координат проекта, зависит от выбора отсчётного геометрического элемента ⁵⁰ (линии, поверхности, системы координат). Отсчётным элементом для определения отклонения формы геометрического элемента является номинальная форма геометрического элемента (линия, поверхность), а для определения отклонения расположения – номинальное расположение собственной системы координат элемента в системе координат проекта .

Нормативная база представления геометрии номинальной и реальной геометрии в проектной конструкторской документации, изложена во множестве действующих основополагающих стандартов, среди которых наибольший интерес для этой статьи представляют:

• 1.    ГОСТ 24642-81. Допуски формы и расположения поверхностей ,

• 2.    ГОСТ 25142-82. Шероховатость поверхности. Термины и определения.

• 3.    ГОСТ 31254-2004. Основные нормы взаимозаменяемости Геометрические элементы. Общие термины и определения.

• 4.    ГОСТ 21495-76 Базирование и базы в машиностроении.

Эта нормативная база отстала от требований времени.

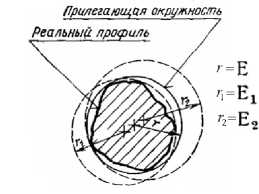
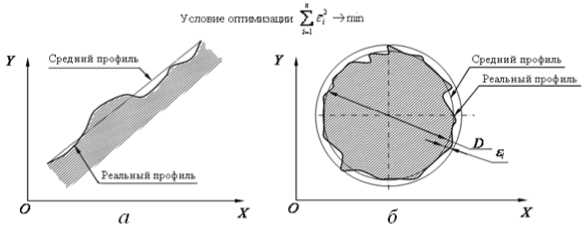
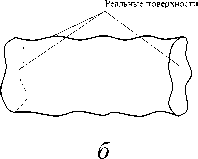
В стандарте [3] для отклонений формы и расположения реальных элементов без кривизны (прямая линия и плоскость) и с постоянной кривизной (окружность, цилиндр) в качестве отсчётных элементов используются прилегающие элементы , имеющие форму номинальных элементов, соприкасающихся с реальными элементами и расположенные вне материала детали так, чтобы максимальное отклонение Е max прилегающих элементов от наиболее удаленной точки реальных элементов имело минимальное значение (рис. 1). Формально это соответствует условию оптимизации Е max →min.

Лрилегаюцдя прямая

Условие оптимизации

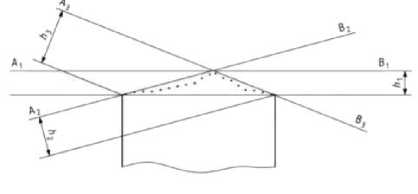
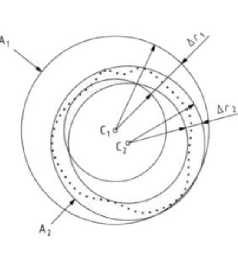
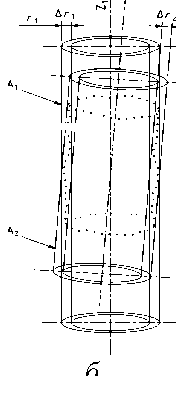
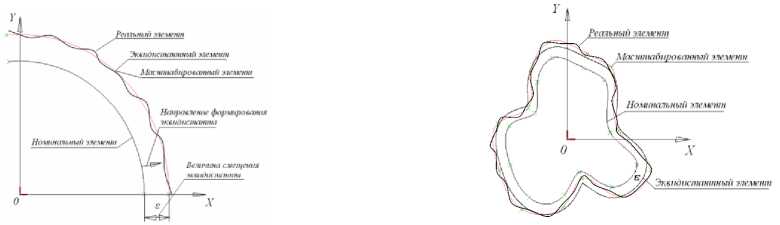
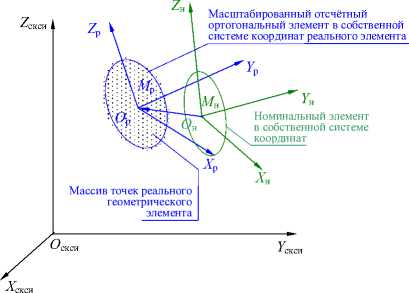
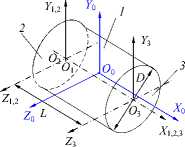
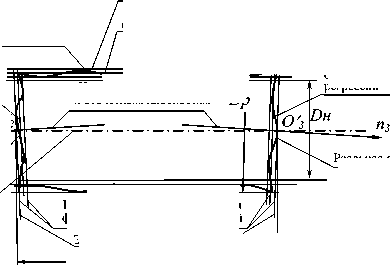
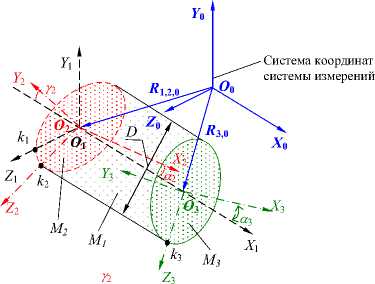
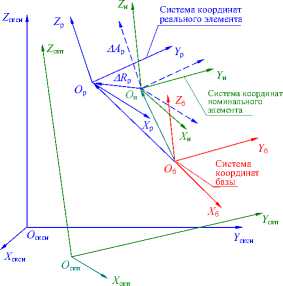
e

б

а

Рис. 1. Прилегающие элементы: а – элемент без кривизны; б – элемент с постоянной кривизной

Международный стандарт [6] отклонение формы реальных геометрических элементов без кривизны, «похожих» на номинальные, (например, прямую линию и плоскость) определяет по минимальной величине зазора h между отсчётными прилегающими элементами, имеющими форму номинальных, и расположенными параллельно по обе стороны от реального геометрического элемента. Формально это соответствует условию оптимизации h→min (рис. 2).

а

Рис. 2. Отсчётные прилегающие элементы для геометрических элементов без кривизны: а – отклонение формы реальной линии,«похожей» на прямую от прямой; б–отклонение реальной поверхности, «похожей» на плоскость от плоскости

б

Отклонения формы геометрических элементов с постоянной кривизной (окружность, цилиндр) рекомендуется определять по минимуму зазора между прилегающими окружностями и цилиндрами минимальной и максимальной зон51 (рис. 3).

а

б

Рис. 3.Отсчётные прилегающие элементы для геометрических элементов с кривизной: а – отклонение формы реального замкнутого контура от круга; б – отклонение формы реальной поверхности «похожей» на цилиндр от цилиндричности

Выбор прилегающих элементов в качестве отсчётных элементов для определения отклонений формы для геометрических элементов, «похожих» на прямую, плоскость, круг и цилиндр не обеспечивает определения отклонения формы реальных элементов от номинальных элементов и однозначности расположения прилегающих элементов в системе координат системы измерения среди измеренных точек реальных элементов. Остальные формы линий и поверхностей в [3] и [6] не рассматривались.

Способы привязки полученного отклонения формы к реальной геометрии и определения собственных систем координат к номинальным и прилегающим элементам, необходимые для количественной оценки отклонения расположения, в [3] и [6] не объяснены, а само определение указанных систем координат носит произвольный характер.

Тем не менее, вся существующая нормативная база для определения отклонений формы и расположения построена на прилегающих элементах.

В стандарте [3] оценку отклонения формы реальных элементов допускается осуществлять с помощью средних элементов52, имеющих номинальную форму, расположенных среди точек реальных элементов, и такие размеры, чтобы сумма квадратов расстояний между реальным и средним элементом в пределах нормируемого участка имела минимальное значение (рис. 4).

Рис. 4. Средние элементы: а – элемент без кривизны; б – элемент с постоянной кривизной

Стандарт [5] по умолчанию (без точного определения понятия средний элемент) использует средние элементы в качестве отсчётных элементов для определения отклонений формы реального элемента каждой из трех областей:

• -    при формулировании технических требований, при рассмотрении отдельных частей будущей детали, опираясь на 2D чертёжную документацию;

• -    при физической материализации детали без построения 3D моделей детали, необходимых для изготовления деталей на станках с ЧПУ с поверхностями, не отличающимися от плоскости, цилиндра и конуса;

• -    в области контроля, когда используются части данной детали при двухточечной оценке⁵³ измеряемых геометрических параметров детали,

• -    а также для уяснения взаимосвязи между этими областями.

В стандартах [3, 4, 5, 6] понятие отклонение расположения реальных элементов строго не определено, отклонение расположения элементов не связывается с собственными системами координат номинальных и реальных элементов. Внимание уделено только деталям с плоскими, цилиндрическими и конусными поверхностями. Нет определения отклонений формы от номинальной поверхности любой формы. Правила привязки системы координат к реальной и номинальной геометрии отсутствуют. Все термины и их определения идут от номинальной геометрии поверхностей детали без связи с технологией и СТО, определяющих реальную геометрию.

Средние геометрические элементы для геометрических элементов без кривизны (прямых линий) можно определить, как геометрические элементы ортогональной средней квадратической регрессии⁵⁴ [7]. Эту же идею можно перенести вначале на плоскость, а затем и на любые геометрические элементы с кривизной (линии, поверхности) [8]. Такие отсчётные элементы можно назвать отсчётными ортогональными элементами. Для них в определении среднего геометрического элемента ошибочно применённое понятие размер целесообразно заменить синонимичным понятием величина.

До сих пор во всех нормативных документах, связанных с определениями отклонений реальной геометрии геометрически элементов от номинальной геометрии, речь шла только об отклонении формы и расположения реального геометрического элемента, и нигде в нормативных документах не упоминалось о таком геометрическом свойстве как величина геометрического элемента.

Величина ортогонального элемента, обусловленная определением по минимуму суммы квадратов отклонения точек реального элемента от отсчётного ортогонального элемента, может быть, как равной, так больше или меньше величины номинального элемента.

Если отсчётный ортогональный элемент имеет форму и величину номинального геометрического элемента, то отклонение точек реального элемента определяется по нормали к номинальному элементу, что и требовалось по смыслу для оценки отклонения формы.

При отличии величины реального геометрического элемента от величины номинального геометрического элемента нужно, прежде всего, сохранить положение системы координат номинального элемента в системе координат системы измерения, необходимое для определения отклонения формы, определяемой для каждой точки реального геометрического элемента по нормали к номинальному геометрическому элементу. Это возможно либо для эквидистанты⁵⁵ к номинальному элементу [9, 10, 11], либо для изменённого масштаба номинального элемента [13] в собственной системе координат номинального элемента. Неопределённость термина форма элемента допускает такую замену для номинальной формы элемента.

Изменённый масштаб номинального элемента при выборе начала собственной системы координат номинального элемента в качестве точки, относительно которой осуществляется масштабирование и эквидистанта к номинальному элементу, обеспечивают как достаточную величину элемента, которой соответствует ортогональная регрессия, так и совпадение положения систем координат номинального и вновь образованных отсчётных элементов.

В случаях, когда элемент не имеет кривизны (прямая или плоскость) или постоянную кривизну (дуга окружности или цилиндр) оба варианта отсчётных ортогональных элементов имеют одинаковую форму элемента (рис. 5, а). Для других форм элементов форма эквидистанты отличается от формы номинального элемента (рис. 5, б).

а                                          б

Рис. 5. сравнение отсчётных элементов: а – дуга, б – элемент произвольного вида

Масштабирование номинального геометрического элемента по предложенным правилам, необходимое для обеспечения величины элемента, которой соответствует ортогональная регрессия, пригодно для элемента любой формы и величины, а собственная система координат реального элемента совпадает с собственной системой координат номинального элемента. Поэтому масштабируемый отсчётный ортогональный элемент предпочтительнее.

Если к отсчётному ортогональному элементу построить эквидистанты нижней и верхней границ отклонения формы реального элемента, то между ними будут находиться отклонения формы, обусловленные шероховатостью⁵⁶ и волнистостью⁵⁷ (рис. 6).

Y

Реальный элемент

Эквивалентный элемент

Номинальный элемент

Масштабируемый отсчётный ортогональный элемент

Эквидистанты к масштабируемому

X отсчётному ортогональному

Отклонение формы, обусловленное волнистостью и шероховатостью

Отклонение формы, обусловленное масштабированием

Рис. 6. Сопоставление геометрии реального и номинального элементов

Отклонение формы реального элемента состоит из двух компонент:

• -    первая обусловлена отклонением величины реального элемента от величины номинального элемента, обусловленным масштабированием;

• -    вторая - предельным эквидистантным отклонением формы реального элемента от масштабируемого отсчётного элемента, обусловленным волнистостью и шероховатостью и обеспечивающим максимум материала детали.

У реального геометрического элемента с постоянной кривизной предельное отклонение формы отсчётного ортогонального элемента относительно номинального постоянно по всему периметру реального геометрического. Для элемента с переменной кривизной отклонение формы отсчётного ортогонального элемента от номинального геометрического элемента не может быть постоянным по всему реальному геометрическому элементу из-за непостоянного расстояния между контурами номинального и масштабированного элементов.

Реальный элемент, ограниченный эквидистантой к наибольшему отклонению точек реального элемента от масштабируемого ортогонального отсчётного элемента, которой соответствует максимум материала детали целесообразно назвать эквивалентным геометрическим элементом или короче эквивалентом, похожим на прилегающий элемент по ГОСТ 24642-81, но определённым по другим правилам. Отклонение формы эквивалентного элемента совпадает с правилами, изложенными в [6], вместе с привязкой этого отклонения к реальному геометрическому элементу.

Расположение собственной системы координат несимметричного отсчётного ортогонального геометрического элемента произвольной формы при равномерном распределении конечного числа измеренных точек по реальной поверхности детали однозначно определяется среди координат случайных точек в системе координат системы измерения по минимуму квадратов отклонений от границы контура геометрического элемента (линии, поверхности) [9]. Система координат отсчётного ортогонального элемента совпадает с собственной системы координат реального элемента в системе координат системы измерения.

Наиболее убедительно алгоритм определения отклонения формы и расположения реального несимметричного геометрического элемента (поверхности) можно продемонстрировать на геометрическом элементе трёхосный эллипсоид, представленном в системе координат проекта. После изготовления и измерения с помощью КИМ реального элемента в системе координат системы измерения Oскси, Xскси, Y скси, Z скси может быть получен массив точек реального геометрического элемента (рис. 7).

Рис. 7. К определению положения масштабированного отсчётного ортогонального элемента в системе координат системы измерения

Для оценки отличия геометрии реального элемента от проекта, поместим начало собственной системы координат Oн номинального трёхосного эллипсоида в произвольную точку системы координат системы измерения и направим оси его собственной системы координат Xн, Yн, Zн в произвольно выбранное направление.

Изменяя масштаб номинального элемента, перемещая начало координат и поворачивая собственную систему координат масштабированного номинального элемента в системе координат системы измерения, определим их величины, обеспечивающие наименьшую сумму квадратов отклонений точек реального элемента от масштабируемого, характерную для отсчётного ортогонального элемента.

Такая процедура в математике называется оптимизацией.

Выполним одновременно или последовательно описанные выше действия и определим в системе координат системы измерения:

• -    значения масштаба номинальной геометрии,

• -    координаты положения начала Oр системы координат отсчётного ортогонального элемента среди измеренных точек реальной поверхности;

• -    величины направляющих косинусов осей координат Xр, Yр, Zр матрицы Aр в системе координат системы измерения Oскси Xскси, Yскси, Zскси.

• -    при которых сумма квадратов отклонений точек реального элемента от ортогонального элемента будет минимальной.

Проведенная оптимизация определяет положение собственной системы координат реального несимметричного элемента в системе координат системы измерения и его величину, необходимую для определения состава геометрических параметров реальной поверхности.

Собственную систему координат реальных геометрических элементов, представленных в номинальной геометрии детали плоскостями и поверхностями с осевой и центральной симметрией, формируют по направлению и координатам двух реперных точек, как это делается в практике предприятий авиационного и ракетно-космического машиностроения с начала сороковых годов прошлого века [9, 10, 11].

Направление одной из осей собственной системы координат реальной плоскости и поверхности вращения совпадает с направлениями нормали или оси вращения. Направление двух других осей собственных систем координат геометрических элементов с осевой симметрией (цилиндр и поверхности вращения) требует указания координат реперной точки, измеренной на реальном геометрическом элементе. Одна из измеренных точек принадлежит эквиваленту геометрического элемента, другая - пересечению вычисленных нормали к ортогональной плоскости или оси вращения с эквивалентами соответствующих реальных поверхностей.

Для элементов с центральной симметрией (окружности и сферы) также требуется указание координат реперной точки, измеренной на реальном геометрическом элементе. Собственная система координат реального геометрического элемента, соответствующего в системе координат проекта элементу с центральной симметрией в системе координат системы измерения выполняется по произвольному направлению одной из осей собственной системы координат геометрического элемента с центральной симметрией и реперной точке.

Простейший пример детали, имеющей номинальные поверхности с осевой и центральной симметрией – вал (рис. 8, а), ограниченный боковой поверхностью с цилиндрической номинальной геометрией поверхности (1) и двумя плоскими торцами (2, 3).

а

Рис. 8. Способы представления геометрии деталей с осевой и центральной симметрией: поверхностей детали в CAD: а – номинальные поверхности в 3D; б – реальные поверхностей после изготовления

Реальную геометрию поверхности детали получают после изготовления из заготовок по выбранному технологическому процессу на выбранных СТО (рис. 8 б) и измеряют в данном случае с помощью 3D КИМ.

Описанная выше оптимизация с помощью масштабированного отсчётного ортогонального элемента (рис. 9) позволяет для перечисленных поверхностей определить в системе координат системы измерения:

• -    величину эквивалентов реальных геометрических элементов, «похожих» на поверхности с осевой и центральной симметрией,

• -    направления осей тел вращения и нормалей к плоскостям,

  _-

  
  

координаты точек, принадлежащих эквивалентам плоскостей, центрам сфер и осям поверхностей вращения.

n2

Эквивалентный цилиндр

Отсчётная эквидистанта

Границы коридора отклонения формы

^

Плоскость ортогональной регрессии

Реальная поверхность

O′2

Плоскость ортогональной регрессии

Реальная поверхность Ось номинального и эквидистантного цилиндра

Эквивалентные плоскости

Lр

Рис. 9. Геометрия реальной детали в 2D

Направление нормалей к отсчётным плоскостям

Реальная поверхность

Границы коридоров отклонения формы от отсчётных плоскостей

Для привязки прямоугольной системы координат к поверхностям с осевой или центральной симметрией на поверхностях номинальной и реальной геометрии необходимо координировать направление и две точки (два репера), принадлежащих каждой из поверхностей. Такими направлениями являются направления оси поверхности «похожей на цилиндр» и нормалей и нормали к поверхностям, «похожим на плоскости». Точками для эквивалента поверхности «похожей на цилиндр» являются точка О′1, принадлежащая оси, и точка k1, принадлежащая цилиндрам номинальному и реальному. На эквивалентах реальных поверхностей торцов «похожих на плоскости» направления нормалей и точки О′2, k2, О′3 и k3, принадлежащие эквивалентам поверхностей торцов номинальному и реальному (рис. 10).

Рис. 10. Формирование систем координат реальных поверхностей с центральной и осевой симметрией

Определение геометрических параметров основных геометрических элементов детали возможно, если в составе исходных данных для обработки войдут не только результаты измерения координат точек реальной поверхности детали, отнесённые к каждой поверхности, но и 3D модель номинальных поверхностей детали, позволяющую построить собственные системы координат номинальных поверхностей.

Отклонение величины реального элемента определяется соотношением между найденной величиной масштабирования Мр отсчётного ортогонального элемента и единицей, соответствующей масштабу Мн номинального элемента.

Отклонение расположения каждого из геометрических элементов определяются в системе координат базы, одинаковой для одноимённых сравниваемых элементов [12]. Такой базой может быть собственная система координат одного из геометрических элементов одинакового в системах координат проекта и системе координат системы измерения (рис. 11, а).

а

б

Рис. 11. Расположение собственных систем координат номинальных и реальных геометрических элементов: а – взаимное положение системы координат системы измерения и системы координат проекта при привязке к системе координат базы, общей для обеих систем координат; б - расположение собственных систем координат номинального и реального элементов в системе координат базы

В системе координат базы, одинаковой для одноимённых сравниваемых элементов, расположение системы координат номинальной поверхности в системе координат базы можно

	" 11 н	l2н	13. ~
представить вектором Rн и матрицей Ан =	ml н	m2н	т 3 .	, а системы координат реальной
	_ nl н	n2н	n 3 н _
li р	l2р	3р
поверхности вектором Rр и матрицей Ар = тх	m2р	m3р	.(рис. 11, б)
_ ni р	n2р	n 3 р _

Отклонение расположения реального элемента относительно расположения номинального элемента имеет две компоненты:

• -    первая компонента обусловлена вектором смещения Дрн начала координат собственной системы координат реального элемента Oр по отношению к началу собственной системы координат номинального элемента Oн;

• -    вторая компонента обусловлена матрицей дополнительного поворота ДАрн матрицы направляющих косинусов Ар собственной системы координат реального элемента относительно матрицы направляющих косинусов Ан собственной системы координат номинального элемента [12].

Все погрешности расположения удобнее всего определять в системе координат номинального геометрического элемента.

Расположение системы координат реальной поверхности в системе координат номинальной поверхности можно представить, как сумму расположения номинальной поверхности, представляемой вектором Rн и матрицей Ан и погрешности расположения представляемой вектором смещения Дрн и матрицей дополнительного поворота ДАрн системы координат реальной поверхности:

Дрн = АТн • (Rр - Rн),

ДАрн = AТн • A р, где АТн - транспонированная матрица.

Длину вектора ARрн можно определить по расстоянию между началами координат реального \и нормального геометрических элементов в системе координат базы по формуле

ARрн = J(Х_о - Х_о )2 = (у₀- Y_o )2 + (z_o - Z_o )2.

р    н     рн     р   н

Дополнительный поворот системы координат можно представить двумя углами а и 8 (а - угол между осью XР и Xн, 8 - угол между осью YР и Yн) [13]. Третий угол ц между осью Zр и Z'о из-за ортогональности осей координат определяется автоматически.

Косинусы углов а и 8 определяются по формулам:

COS а = l^ 11р + m^mlр + n 1н niр , COS 8 = l2рl2р + m2нm2р + n2н n2р откуда а = arcos ( liH 11р + т1нmlр + n 1н niр ) И 8 = arcos ( l2р12р + m2нm2р + n2нn2р ).

Вычислить численные значения характерных размеров геометрических элементов реальной детали можно по исходной 3D модели и результатам адекватной обработки данных измерения координат точек реальных деталей, полученных с помощью координатно-измерительных машин.

Отклонение формы реального элемента определяются по отклонению точек реального элемента по нормали к номинальному элементу.

В результате обработки данных координатно-измерительных машин в системе координат системы измерения можно определить величину эквивалентов реальных элементов, вычислить расстояния между началами собственных систем координат реальных геометрических элементов, направления осей систем координат эквивалентов элементов, а также отклонения величины, формы и расположения всех реальных геометрических элементов детали на всех стадиях жизненного цикла детали.

Выводы

Наиболее полную и достоверную информацию о реальной геометрии детали можно получить с помощью 3D координатно-измерительных машин. Для решения задач прямого инжиниринга целесообразно рассматривать геометрические элементы детали с привычных позиций назначения допустимых ограничений формы и расположения поверхностей.

Выбор средних геометрических элементов в качестве отсчётных элементов для определения отклонений формы и расположения реальной геометрии от номинальной геометрии геометрических элементов обеспечивает однозначное определение геометрических параметров элементов реальной детали (величины, расположения, формы реальных геометрических элементов) и их отклонений от номинальной геометрии.

Средние геометрические элементы можно определить, как геометрические элементы ортогональной средней квадратической регрессии. Положение системы координат геометрического элемента произвольной формы среди координат случайных точек определяется по минимуму квадратов отклонений от границы геометрического элемента. Такие отсчётные элементы, названные отсчётными ортогональными элементами, масштабируемые при изменении величины реального геометрического элемента относительно начала координат номинального геометрического элемента, позволяют определить отклонения формы для несимметричных и симметричных геометрических элементов любой величины и формы. После всех приведенных обоснованных понятий и доказательств, появилась возможность ответить на все вопросы, относящиеся к геометрии любых реальных недеформируемых деталей машиностроения.

Разработанная теория сравнения реальной геометрии деталей машиностроения с номинально геометрией может быть положена в основу раздела практической метрологии геометрических параметров технических изделий. Такая теория обеспечивает вычисление всех размеров, определяющих объём детали, параметры отклонения величины, формы и расположения всех реальных поверхностей детали по данным измерения реальных поверхностей деталей координатно-измерительными машинами и сравнения их с 3D моделями деталей.

Эта же теория может быть положена в основу разработки нового поколения САПР, обеспечивающего в отличие от существующих систем, моделирование геометрии недеформируемых деталей, ограниченных реальными поверхностями, с последующим переходом к моделированию сопряжения реальных поверхностей деталей, сборки деталей и оценки изменения геометрии изделия после сборки.