Создание идеального изображения объекта на основе гармонических свойств полного четырехугольника

При формировании изображений невозможно избежать появления различного рода погрешностей, вызванных несовершенством аппаратной части, например, некачественной сборкой системы линз. Одним из типов погрешностей цифровых изображений является дисторсия изображения, когда изображение квадрата искажается и принимает вид «бочки» или «подушки». Дисторсия также обычно возникает при изменении фокусного расстояния камеры при съемке.

Традиционным подходом к определению дисторсии оптических систем является использование специально созданного идеального объекта, расположенного в заданной плоскости рабочей сцены, по изображению которого производится определение искажений.

Метод определения погрешностей оптических аберраций

В качестве тестового объекта была выбрана квадратная сетка. Выбор обоснован тем, что изображение квадратной сетки дает более полную картину наличия погрешностей по всему изображению. Для получения экспериментальных данных использовались сетки разных размеров. Тестовый объект размещался на предметной плоскости, располагаемой под определенным углом к оптической оси камеры.

На рисунке 1 приведено реальное цифровое изображение тестового объекта.

Рис. 1. Реальное изображение квадратной сетки

В работе принимается допущение, что в центральной части реального цифрового изображения погрешности оптических аберраций малы и ими можно пренебречь. Принимая за основу это допущение, по центральной части реального изображения на основе свойств полного четырехугольника [1] создают изображение сетки без искажений, которое далее в работе будем считать идеальным изображением. Тогда погрешности оптических аберраций определяют по разнице координат соответствующих узловых точек реального и идеального изображений сетки.

Метод построения идеального изображения сетки

Рассматриваемая задача относится к задачам центрального проецирования. Квадратная сетка, расположенная на предметной плоскости, проецируется на плоскость изображения. Проекция сетки на плоскость изображения представляет собой совокупность разных по размеру четырехугольников. Зная размеры любого из этих четырехугольников, можно восстановить все изображение сетки на основе гармонических свойств полного четырехугольника.

На рисунке 2 фигура ABCD представляет собой полный четырехугольник, имеющий три пары противоположных сторон AB и CD, AC и BD, AD и BC. Точки пересечения противоположных сторон, называемые «диагональными точками», на рисунке 1 обозначены как:

AB x CD=K; AD x BC=L; AC x BD=M.

Прямые, соединяющие диагональные точки, называемые «диагоналями», обозначены как прямые KL, LM и MK. Точки пересечения диагонали KL со сторонами BD и AC обозначены соответственно буквами F и G∞. Точка G∞ является несобственной точкой пересечения параллельных линий, проходящих через точки A, C и K, L.

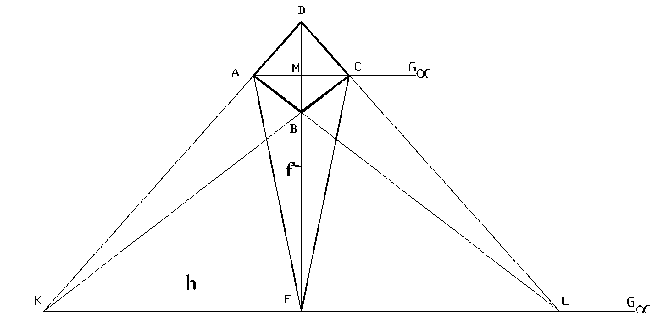
Рис. 2. Изображение центрального квадрата сетки

Согласно гармоническим свойствам полного четырехугольника имеются гармонические группы точек на каждой его диагонали и на каждой его стороне [1]. На каждой диагонали полного четырехугольника гармоническая группа точек образована двумя диагональными точками (K и L) и точками пересечения (F и G∞) этой диагонали с парой сторон, проходящих через третью диагональную точку M. На каждой его стороне гармоническая группа точек образована парой вершин (A и C), диагональной точкой M и точкой пересечения (G∞) этой стороны с диагональю, проходящей через две другие диагональные точки. Таким образом, имеем (ACMG∞)=(KLFG∞)=-1.

Согласно инвариантности сложного отношения при всех его проектированиях и пересечениях имеем замечательное свойство, заключающееся в том, что при каждом переходе от пучка или ряда к перспективному ряду или пучку сложное отношение не изменяется [1]. В рассматриваемой задаче, если провести пучок прямых через точки A и C из центра F, будем иметь несколько проективных форм первой ступени, у которых сложные отношения любых четырех пар соответственных элементов равны.

Изложенные выше свойства полного четырехугольника можно применить к рассматриваемой задаче. Диагональные точки K и L, являющиеся точками пересечения противоположных сторон, будут являться точками схода. Диагональ четырехугольника KL, соединяющая точки схода, будет являться линией горизонта h. В рассматриваемом примере линия f, проходящая через точки D, B и F, перпендикулярная линии h, представляет собой линию наибольшего наклона плоскости изображения к предметной плоскости. В общем случае линия f не всегда будет совпадать с линией наибольшего наклона плоскости изображения к предметной плоскости (это зависит от расположения реальной сетки на предметной плоскости).

Эти свойства полного четырехугольника и инвариантности сложного отношения позволяют построить изображения смежных четырехугольников (см. рис. 3). Для этого продолжим линии LD и FA до пересечения в точке A’, линии KD и FC – до пересечения в точке C’. Затем продолжим линии KA’ и LC’ до пересечения в точке D’. Тогда фигура A’D’C’D’ представляет собой изображение смежного верхнего четырехугольников сетки, причем точка B’ совпадает с точкой D. Аналогично можно построить изображение смежного нижнего четырехугольников A ″ B ″ C ″ D ″ .

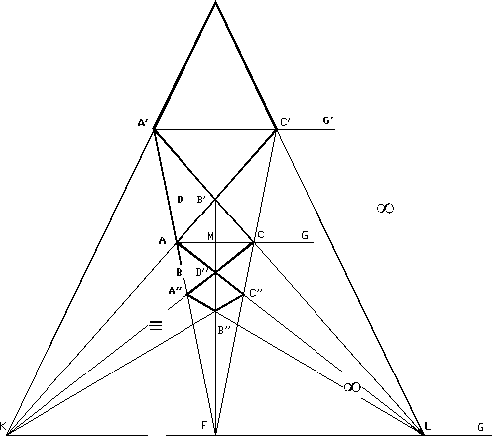
Рис. 3. Создание изображений смежных квадратов сетки

Для определения погрешностей формирования цифровых изображений необходимо иметь информацию по всему полю изображения. Поэтому при построении изображения идеальной сетки необходимо достраивать изображение до тех пор, пока все поле изображения не будет покрыто сеткой. На рисунке 4 приведен пример построения фрагмента идеальной сетки, состоящей из 9 четырехугольников.

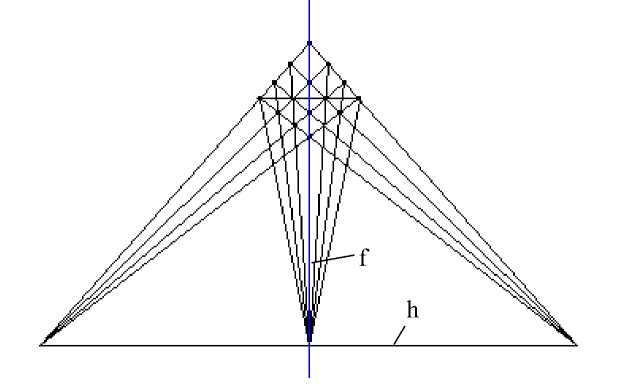
K                    F                 L

Рис. 4. Фрагмент идеальной сетки

Для проверки корректности построения идеальной сетки было выполнено геометрическое моделирование задачи в графическом пакете AutoCAD. Ниже приводится рисунок 5, иллюстрирующий моделирование задачи в трехмерном пространстве.

На рисунке 5 введены следующие обозначения: S – точка оптического центра, λ ‒ предметная плоскость, на которой находится квадратная сетка, π ‒ плоскость изображения, точки K и L – точки схода, h – линия горизонта, f – линия максимального наклона плоскости изображения к предметной плоскости, точка F – точка пересечения линии горизонта и линии максимального наклона.

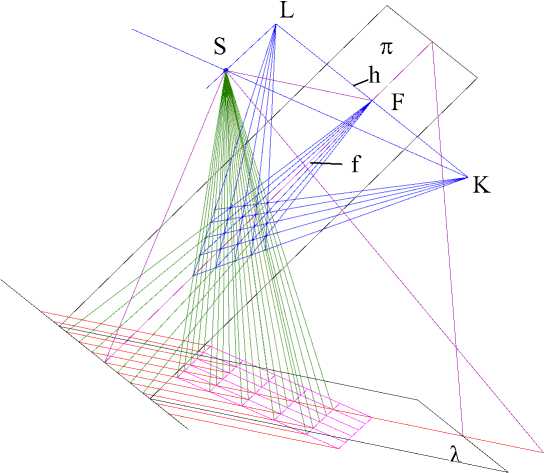
Рис. 5. Моделирование задачи построения идеальной сетки в трехмерном пространстве

Программная реализация задачи

Программная реализация алгоритма по восстановлению линий изображения идеальной сетки проводилась по следующей методике:

• 1.    Определение координат вершин исходного четырехугольника в центральной части кадра.

• 2.    Построение идеального изображения сетки.

• 3.    Определение погрешностей оптических аберраций.

Среди точек центрального четырехугольника выделяются угловые точки – его вершины (точки A, B, C, D), по которым вычисляются координаты диагональных точек K и L, и точка пресечения диагоналей KL и BD – точка F (рис. 6). Затем с учетом гармонических свойств полного четырехугольника, строятся четырехугольники, лежащие на диагональной прямой FD, в области, ограниченной точками FADC, смежные центральному четырехугольнику (рис. 7).

Вычисление координат узлов сетки

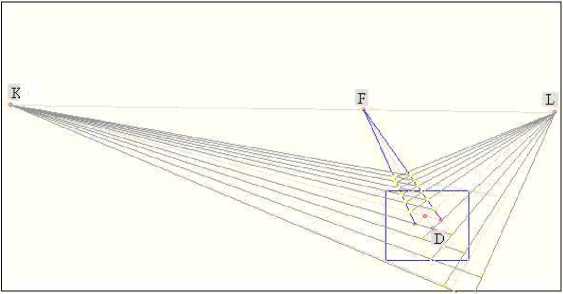
Рис. 7. Вычисление координат четырехугольников, смежных центральному

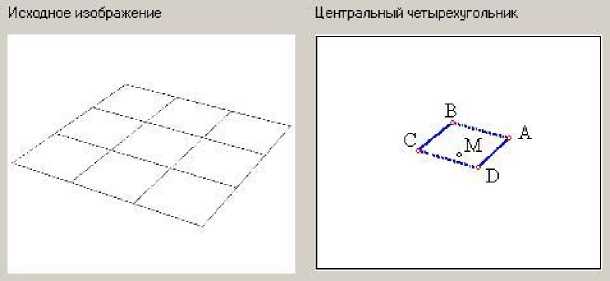
Рис. 6. Выделение центрального четырехугольника и его вершин

Последовательно вычисляя точки пересечения всех прямых, проходящих через вершины центральных четырехугольников, определяем координаты всех узлов идеальной сетки (рис. 8).

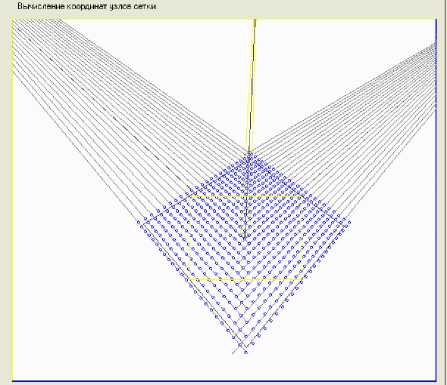
Рис. 8. Узловые точки идеальной сетки

Заключение

Использование гармонических свойств полного четырехугольника позволило создать идеальное изображение с минимальными погрешностями оптических аберраций.

Геометрическое моделирование задачи в графическом пакете AutoCAD и результаты программной реализации разработанного метода показали корректность метода создания идеального изображения по центральной части реального изображения.

Данный метод позволит определить характер возникающих погрешностей и корректировать контур реального изображения, что, в конечном счете, увеличит точность обмера исследуемых объектов.

Проблема повышения точности восстановления контура исследуемых объектов имеет важное прикладное значение. Например, позволит увеличить точность калибровки систем технического зрения, что немаловажно для интеллектуальных робототехнических комплексов.