Создание искусственной силы тяжести при помощи колебательных систем, имеющих силовые характеристики с участками квазинулевой жесткости

Проблема создания искусственной силы тяжести при длительных космических полетах в настоящее время стоит достаточно остро. Как показали исследования доктора медицинских наук Оганова, процесс восстановления нормальной минеральной плотности человека при космическом полете занимает в 2–3 раза больше времени, чем длится сам полет, и после продолжительных космических экспедиций растягивается на годы [8].

В настоящее время для создания искусственной силы тяжести в основном применяются центрифуги: влияние на организм человека сил инерции эквивалентно влиянию сил тяжести. Доктором медицинских наук Волеговым предложены тренажеры для космонавтов, в которых используются силы инерции, возникающие при возвратнопоступательных колебаниях [3].

В 2011 г. НАСА предложило проект космической станции («Наутилус-Х»), один из модулей которой будет вращаться, обеспечивая искусственную гравитацию в 0,11– 0,69 g . Диаметр вращающегося модуля равен 9,1 либо 12 м, а сам модуль будет служить спальным местом для шести космонавтов [10]. Но полученная в этом случае микрогравитация, по-видимому, не устранит всех негативных последствий, вызываемых невесомостью [7]. Получить искусственную гравитацию с перегрузкой 1 g и более в течение продолжительного времени при помощи центрифуг короткого радиуса из-за проблем с вестибулярным аппаратом проблематично. При использовании таких центрифуг центробежные силы, действующие на разные участки тела (голова, …, ноги), различны.

Вопрос возможности применения больших перегрузок (больше 1 g ) при длительных космических полетах в современной научной литературе практически не освещен [2]. С этой точки зрения предлагаемые в статье способы создания искусственной силы тяжести за счет колебательных систем, имеющих силовые характеристики с квазинулевой жесткостью (квазипостоянной силой), при помощи которых возможно получать необходимые повышенные перегрузки, являются весьма актуальными.

Впервые идея использовать колебательные системы с квазинулевой жесткостью для создания необходимой перегрузки при космических полетах была высказана авторами на X съезде по фундаментальным проблемам теоретической и прикладной механики (Нижний Новгород, 24–30 августа 2011 г.) на подсекции «Колебания механических систем» [5] и получила положительные отзывы механиков

Материалы и методы

Системы с квазинулевой жесткостью, когда на рабочем участке силовой характеристики восстанавливающая сила постоянна при изменении координаты точки ее приложения, известны с 70-х годов прошлого века [1]. Они нашли применение в основном в области виброзащиты. Получение систем, имеющих заданные силовые характеристики, в частности с участками квазинулевой жесткости (квазипостоянной восстанавливающей силы), возможно на базе упругого элемента, перемещающегося между направляющими расчетной формы [4, 11].

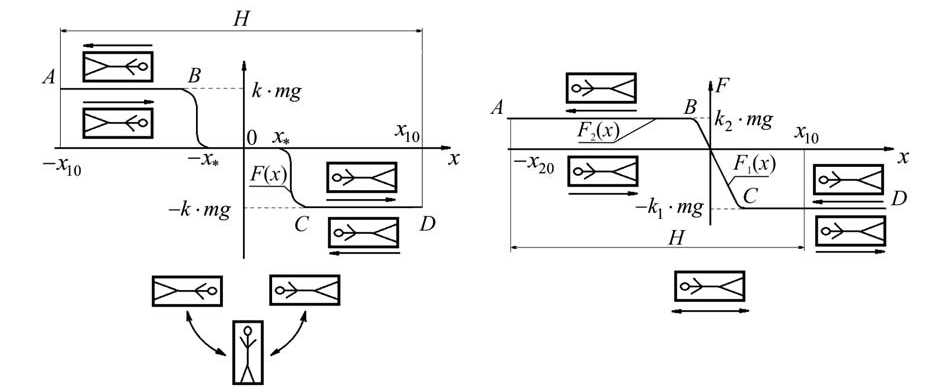
Для создания искусственной силы тяжести предлагается использовать колебательные системы, имеющие силовые характеристики с квазинулевой жесткостью (квазипостоянной восстанавливающей силой), изображенные на рис. 1. На участках AB и CD на космонавта при колебаниях будет действовать необходимая постоянная сила k∙mg ( а ); k 1 ∙mg ; k 2 ∙mg ( б ), где k , k 1 , k 2 – коэффициенты перегрузки; m – масса кабины с космонавтом; g – ускорение свободного падения .

Система с силовой характеристикой, представленной на рис. 1, а , предполагает разворот космонавта дважды на 180 град за период колебаний (участок BC ). Сила воздействия на космонавта инерционных сил при этом будет направлена почти постоянно (за исключением времени разворота) в одну сторону, например со стороны головы в ноги – аналог земного притяжения.

В колебательной системе с силовой характеристикой, представленной на рис. 1, б , разворота космонавта не происходит: на участке CD на космонавта в определенном направлении (на рисунке со стороны ног в сторону головы) действует заданная постоянная восстанавливающая сила k 1 ∙mg. После «плавного» прохождения нейтрального положения (участок СВ ) на космонавта будет действовать восстанавливающая сила k 2 ∙mg , направленная в противоположную сторону.

На рис. 2 представлена видеограмма выполнения гребка, сделанная скоростной видеокамерой. Временной интервал между кадрами составляет 0,004 с. Шаг раскадровки составляет 8 кадров или 8 ∙ 0,004 = 0,032 с.

Данные системы создания искусственной силы тяжести предполагается использовать в первую очередь при длительных космических полетах для ликвидации отрицательного влияния невесомости. Поскольку масса космического аппарата в этом случае может достигать нескольких сотен тонн, а масса кабины с колеблющимся космонавтом 100–200 кг, то можно считать, что колебательные системы с силовыми характеристиками, изображенными на рис. 1, присоединены к неподвижному основанию. Тогда свободные нелинейные колебания кабины с космонавтом, принимаемой за точку, в случае силовой характеристики, изображенной на рис. 1, а , будут описываться следующим дифференциальным уравнением:

m • x = - ( k • mg • th[ k * • (| x | + x * )] + k • mg ) • sign[ x ] / 2 , (1) где m – масса колеблющейся кабины с космонавтом, m = 100 кг; k _* – безразмерный коэффициент, учитывающий форму восстанавливающей силы на участке ВС , к * = 100; x _* – координата, определяющая длину участка разворота, должна быть такой, чтобы позволить разворот космонавта с допустимой угловой скоростью, ограниченной возможностями вестибулярного аппарата космонавтов.

Начальные условия дифференциального уравнения (1) следующие: x 0 = x ₁₀; x₀ = 0, где x ₁₀ - начальное отклонение кабины из нейтрального положения.

а                                             б

Рис. 1. Силовые характеристики предлагаемых колебательных систем для получения искусственной силы тяжести: а – с разворотом; б – без разворота (стрелками указаны направления движения (скорости) кабины с космонавтом)

На рис. 2 представлены зависимости восстанавливающей силы (правая часть дифференциального уравнения (1)), перемещения кабины с космонавтом (100 ∙ x ( t ) ) и ее скорости (100 • x ( t )) от времени, полученные решением дифференциального уравнения (1) при k = 1. Величина x _* должна быть такой, чтобы при заданном значении x ₁₀

средняя угловая скорость кабины ( ωср

π

=    , где

T _*

T _* – время разворота) при развороте на

участке (–x* , …, x* ) (см. рис. 1, а) была не больше заданной, ограниченной возможностями вестибулярного аппарата космонавтов. В данном примере

ω_ср ≈ 0,81 с ^{- 1}

или количество оборотов в минуту n =

ω ⋅ 30

π

7,7. Это больше, чем

«желательное» значение количества оборотов в минуту для центрифуг n* = 2...4, но меньше, чем количество оборотов в минуту, возникающее при работе центрифуг короткого радиуса, предложенных НАСА [10]. Например, как было указано выше, при перегрузке k = 0,69 и радиусе 9,1/2 = 4,55 м количество оборотов в минуту будет n = 11,65. В предлагаемом способе создания искусственной силы тяжести вращение происходит дважды за период колебаний в противоположные стороны. Для определения предельной величины угловой скорости в этом случае необходимы дополнительные исследования.

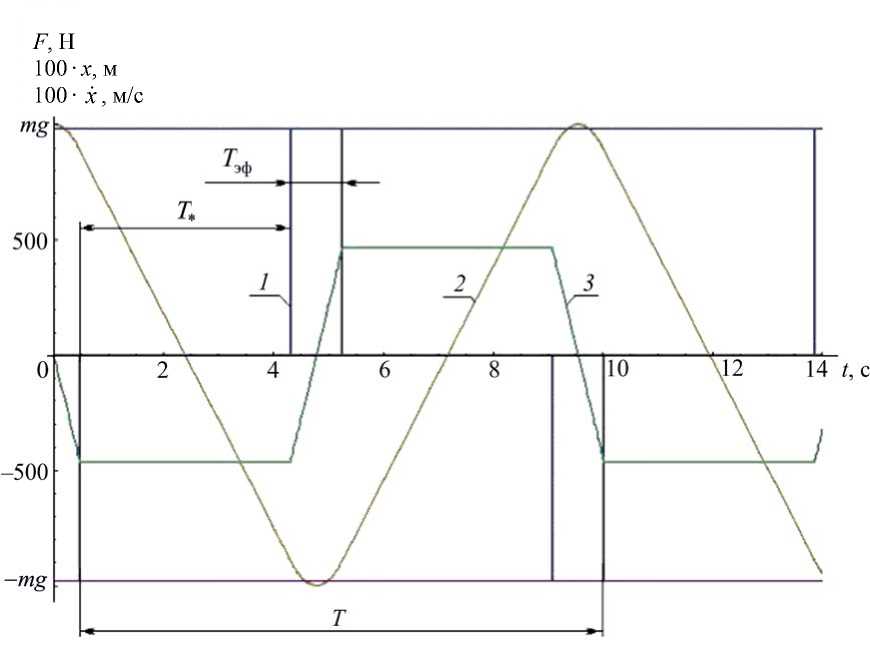
Рис. 2. Зависимости от времени параметров колебательной системы, имеющей силовую характеристику, изображенную на рис. 1, а , при перегрузке k = 1. Восстанавливающая сила (кривая 1 ), перемещение кабины с космонавтом (кривая 2 ) и ее скорость (кривая 3 ) получены численным решением дифференциального уравнения (1) при x _* = – 8,9 м; x ₁₀ = 10 м; H = 2 ⋅ 10 = 20м;

T = 9,5 c; T _*. ≈ 3,9 с; T _* / T _эф ≈ 3,65;ω _ср ≈ 0,81 с ^{- 1}

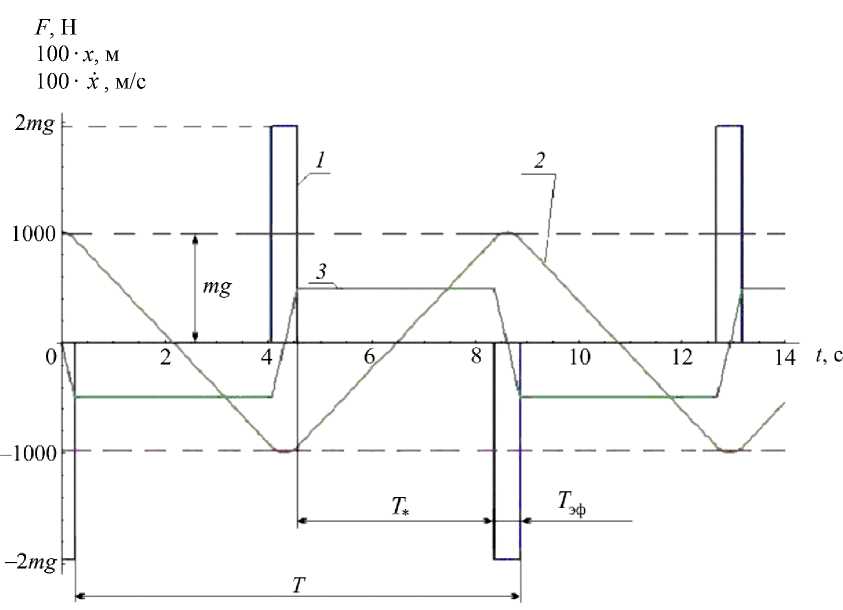
На рис. 3 представлены зависимости восстанавливающей силы, перемещения кабины с космонавтом (100 ■ x ( t )) и ее скорости (100 ■ X ( t )) от времени, полученные решением дифференциального уравнения (1) при перегрузке k = 2 из условия сохранения той же угловой скорости разворота ω_ср ≈ 0,81 с ^{- 1} на участке (– x _* , …, x _*) . Как видно из рис. 2 и 3, отношение T _* / T _эф , где T _эф – время воздействия заданной перегрузки, при увеличении коэффициента k в два раза также увеличилось примерно в два раза.

Зависимости начальных отклонений x ₁₀ ( 1 – k = 1; 3 – k = 2), представленные на рис. 4 и построенные по решениям дифференциального уравнения (1) из условия сохранения средней угловой скорости разворота на участке (– x _* , …, x _* ) (см. рис. 1), оказались практически линейными. Отношения T _* / T _эф ( 2 – k = 1; 4 – k = 2), при том же условии сохранения средней угловой скорости вращения ω_ср , также почти линейно уменьшаются с увеличением x _*.

На рис. 5 представлены зависимости отношений T _* / T _эф от коэффициента перегрузки k , построенные по решениям дифференциального уравнения (1). Как видно из рис. 5, при x ₁₀ = 5 м отношение T _* / T _эф резко увеличивается при увеличении перегрузки k , при x ₁₀ = 15 м отношение T _* / T _эф практически не зависит от перегрузки.

F , Н

100 ∙ x , м

100 • X , м/с

-1000

-2mg

Рис. 3. Зависимости от времени параметров колебательной системы, имеющей силовую характеристику, изображенную на рис. 1, а , при перегрузке k = 2. Восстанавливающая сила (кривая 1 ), перемещение кабины с космонавтом (кривая 2 ) и ее скорость (кривая 3 ) получены численным решением дифференциального уравнения (1) при x _* = – 9,38 м; x ₁₀ = 10 м; H = 2 ⋅ 10 = 20 м;

T = 8,6 c; T _*. ≈ 3,9 с; T _* / T _эф ≈ 7,8;ω _ср ≈ 0,81 с ^{- 1}

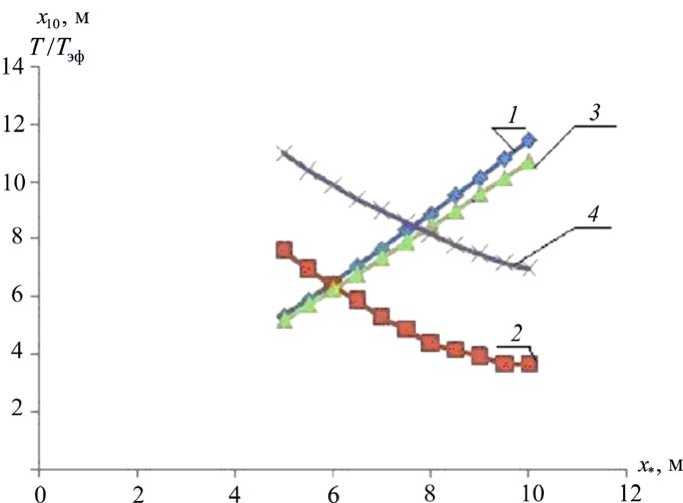
Рис. 4. Зависимости начальных отклонений кабины с космонавтом x ₁₀ ( 1 , 3 ) и отношений Т * / Т эф ( 2 , 4 ) от величины х ₀ , определяющей длину участка разворота

(- x * , ..., x *), при условии сохранения средней скорости разворота ы_ср ® 0,81 с ¹ (получены численным решением дифференциального уравнения (1) по зависимостям типа тех, что представлены на рис. 2, 3); 1 , 2 - к = 1; 3 , 4 - к = 2;

• 1 , 3 - x io ( x * ); 2 , 4 - Т * / Т _эф ( x * ); 1 , 2 - к = 1; 3 , 4 - к = 2

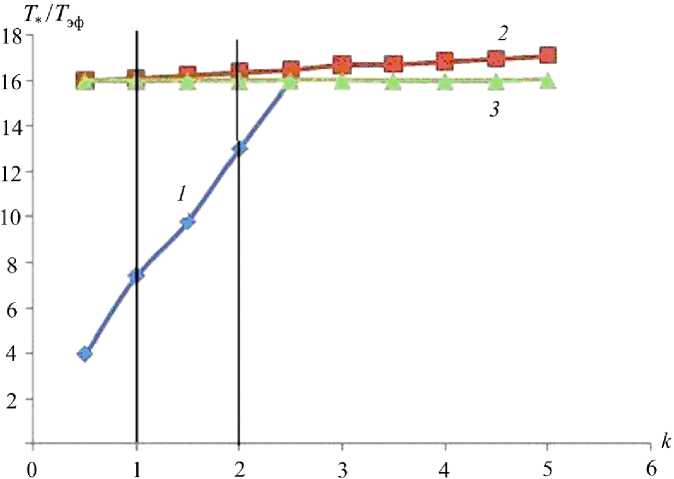
Рис. 5. Зависимости отношений Т * / Т эф от перегрузки к при условии сохранения средней скорости разворота ( ы_ср ® 0,81 с ^{- 1}; 1 - х ₁₀ = 5 м; 2 - х ₁₀ = 10 м; 3 - х ₁₀ = 15 м; получены численным решением дифференциального уравнения (1) по зависимостям типа тех, что представлены на рис. 2, 3). Т * / Т _э ф ( к ): 1,2 , 3 - х 10 = 5 м; х 10 = 10 м; х 10 = 15 м соответственно

Получение повышенных перегрузок ( k > 1) при помощи колебательных систем, имеющих силовую характеристику, изображенную на рис. 1, а , может оказаться недостаточно эффективным из-за больших значений T _* / T _эф : доля времени воздействия перегрузки по отношению к общему периоду колебаний при увеличении T _* / T _эф уменьшается, например для k = 2 при х 10 = 5 м – T _* / T _эф ≈ 13; при х 10 = 15 м – T * / T эф ≈ 16.

При свободных колебаниях упругих систем, имеющих силовую характеристику, изображенную на рис. 1, б , задаваемая восстанавливающая сила k 1 ∙mg , имитирующая силу тяжести, действует на космонавта в течение части периода колебаний (правая часть силовой характеристики). Разворота в данном случае не происходит. После плавного прохождения нулевого положения (участок СВ ) на космонавта будет действовать восстанавливающая сила k 2 ∙mg , противоположная по отношению к k 1 ∙mg (левая часть характеристики). Силовая характеристика в этом случае (см. рис. 1, б ) также была выражена аналитической функцией. Дифференциальное уравнение, описывающее свободные нелинейные колебания в этом случае, следующее:

mx = - ( k₁₀ • m • g • th[ k 3 • x ] + k 20 • m • g • th[ k 4 • x ] • sign[ x ]), (2)

где k 10 , k 20 – коэффициенты, определяющие восстанавливающие силы на участках CD и АВ соответственно; k 1 = k 10 + k 20 ; k 2 = k 10 – k 20 (см. рис. 1, б ); k 3 = 1; k 4 = 0,8 – коэффициенты, определяющие форму и размеры участка ВС (рис. 1, б ).

Начальные условия дифференциального уравнения (2): x 0 = x ₁₀; 5c₀ = 0.

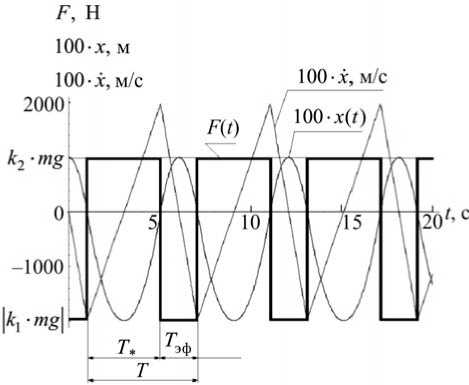
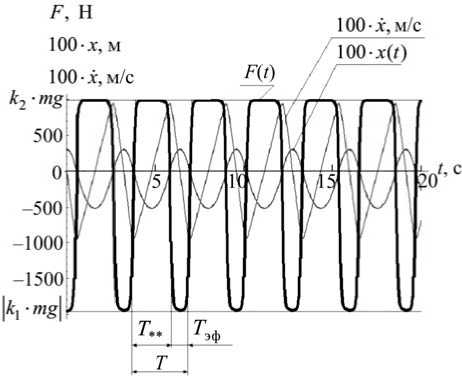
Пусть m = 100 кг; k 1 = 2; k 2 = 1 ( k 10 = 1,5; k 20 = 0,5) . На рис. 6 представлены зависимости восстанавливающей силы F ( t ), действующей на кабину с космонавтом, ее перемещения (100 • x ( t )) и скорости (100 • jc( t )) от времени. Для варианта а - T _** / T _эф ≈ 2, где T _** – время действия силы k 2 ∙mg ; T _эф ≈ 2 с; T ≈ 6с ; для варианта б – T ** / T эф ≈ 1,8; T эф ≈ 1,1 с; T ≈ 3,1с.

Изменяя коэффициенты k 1 и k 2 (о том, как это принципиально сделать, будет сказано ниже), можно получать заданное отношение T _** / T _эф . Вид восстанавливающей силы при этом будет такой же, как на рис. 6. При изменении величины начального смещения х 10 можно получить заданные абсолютные значения T , T _**, T _эф . При помощи колебательных систем, имеющих силовые характеристики, представленные на рис. 1, б , можно получать более высокие перегрузки по сравнению с системами, имеющими силовые характеристики, представленные на рис. 1, а .

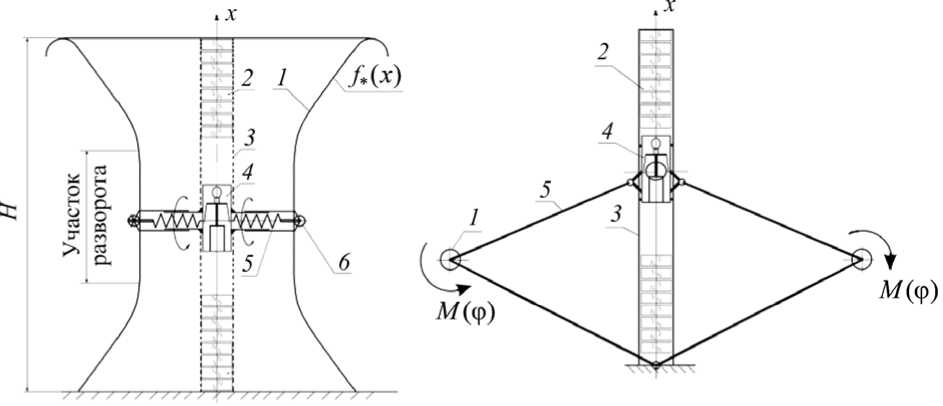
Для получения конструкций систем, имеющих силовые характеристики, изображенные на рис. 1, предполагается использовать колебательные системы на основе упругого элемента, перемещающегося между двумя направляющими расчетной формы [11] (рис. 7, а ), или колебательные системы на основе упругих шарниров с заданными угловыми силовыми характеристиками (рис. 7, б ) [4].

Поскольку для получения искусственной гравитации предлагаемыми методами рассматриваются свободные колебания, то для компенсации диссипативных сил предлагается, в частности, использовать цепочку электромагнитов (см. рис. 7), аналогично тому, как это делается в поездах на магнитной подушке [5]. Другими способами компенсации диссипативных сил могут быть использование возмущающей силы и даже мускульной силы самого космонавта (как на качелях).

Рассмотрим конкретный пример. Рассчитаем форму направляющих f ( x ) (при условии, что радиус роликов равен нулю; f _* ( x ) – функция, определяющая форму направляющих для реального случая, когда радиус роликов не равен нулю) для

а

Рис. 6. Зависимости восстанавливающей силы F ( t ), действующей на кабину с космонавтом, ее перемещения (100 • x ( t )) и скорости (100 • x ( t )) от времени ( m = 100 кг; k 3 = 1; k 4 = 0,8; k 10 = 1,5; k 20 = 0,5; k 1 = 2; k 2 = 1; а – x 10 = 10 м; Т ** / Т эф - 2 ; б — X 10 = 3 м; Т ** / Т эф - 1,8 ; Т = Т эф + Т ** - период колебаний; T _эф – время действия восстанавливающей силы k ₁ ∙ mg ; T _**. – время действия восстанавливающей силы k 2 ∙ mg )

б

б

а

Рис. 7. Схемы конструкций для получения силовых характеристик, представленных на рис. 1; а – при помощи продольных направляющих расчетной формы: 1 – направляющие; 2 – электромагниты; 3 – направляющие кабины; 4 – кабина с космонавтом; 5 – упругий элемент (пружина); 6 – ролик; б – при помощи упругих шарниров с заданными силовыми характеристиками: 1 – упругий шарнир с заданной угловой силовой характеристикой M (φ) ; 2 – электромагниты;

3 – направляющие кабины; 4 – кабина с космонавтом; 5 – стержни

варианта системы, представленной на рис. 8, а , при следующих данных: m = 100 кг; k 1 = 2; k 2 = 1 ( k 10 = 1,5; k 20 = 0,5); x 10 = 10 м; силовая характеристика определяется функцией F ( x ) = - ( k₁₀ • m • g • th[ k ₃ • x ] + k ₂₀ • m • g • th[ k 4 • x ] • sign[ x ]).

Приведем расчет на одном этапе, когда координата х изменяется от 0 до 10 м. Зная на данном этапе восстанавливающую силу F ( x )   (здесь она

F ( x ) = k 1 ₀ • m • g • th[1 • x ] + k ₂₀ • m • g • th[0,8 • x ], см. рис. 1, б ), можно рассчитать функцию fx ), определяющую форму направляющих 1 (см. рис. 7, а ). Зависимость между ними следующая [11]:

∂ П

F ( x ) = —,                                ⁽³⁾

дх где П - потенциальная энергия упругого элемента (в данном случае пружины, см. рис. 8, а), П = с • (f (x) -l0 - b)2; с - коэффициент жесткости пружины; l0 - длина ненапряженной пружины; b - const.

Подставим функции F ( x ) и П( х ) в формулу (3) и определим f ( x ):

k ₁₀ • m • g • th[1 • x ] + k ₂₀ • m • g • th[0,8 x ] = ^[ с ^{( f (} x ) —-—^)-],

∂х кю • m • g • th[x] + k20 • m • g • th[0,8x] = 2 • с • (f (x) -10 - b) • f ‘(x), k10 • m ■ g • th[x]dx + k20 • m • g • th[0,8x]dx = 2 • c • f (x)df (x) - 2 • c • 10 df (x) - 2 • c • b df (x).

Проинтегрировав последнее выражение, получим k10 • m • g • ln[ch[x]] + k20 • m ■ g • 1,25 • ln[ch[0,8x]] = = c• f 2(x)-2• c• 10 • f (x)-2• c• b• f (x) + C0.

Определим постоянную интегрирования Со. При х = 0: f (x) = L0 / 2 (см. рис. 8, а), тогда Cо = c ■ 10 • L0 + c ■ b ■ L0 - c ■ (L02 / 4). Подставляя это выражение в (4), получим k10 • m • g • ln[ch[x]] + k20 • m • g • 1,25 • ln[ch[0,8x]] =

= c • f ²( x ) - (2 • c • 1 ₀ + 2 • c ■ b ) • f ( x ) + c • 1 ₀ • L ₀ + c • b • L ₀ - c • ( L ₀²/4).             ⁽ 5)

Окончательно имеем f (x) = (10 + b) + 4(b +10)2 - D / c,                           (6)

где D = ( c • 1 0 • L ₀ + c • b • L ₀ - c • L ₀² /4) - k ₁₀ • m • g ln[ch[ x ]] - 1,25 • k ₂₀ • m • g • ln[ch[0,8 x ]].

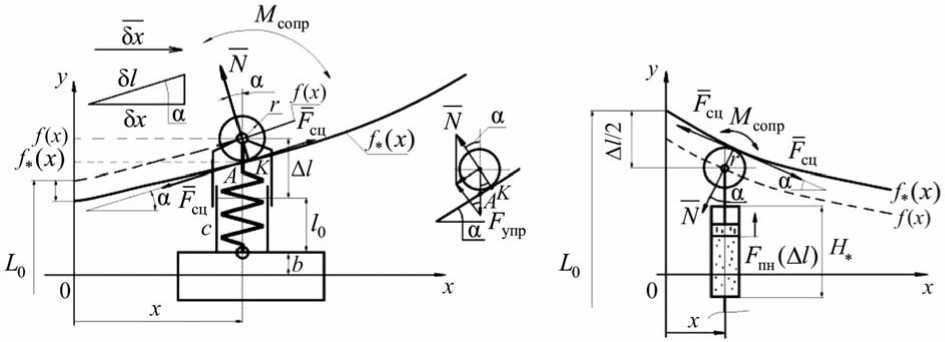
а

б

Рис. 8. Схемы конструкций с направляющими для упругого элемента. Упругие элементы: а - пружина; б - пневмопружина)

Для оценки потерь на трение при движении роликов по направляющим найдем форму направляющих, которая определяется функцией f,(x) , с учетом радиуса ролика r (см. рис. 7, а; 8). Задавая 10 = 0,5 м; L0 = 3,4 м; b = 0,4 м; с = 5000 H/м; r = 0,1 м, по формуле (6) получаем зависимость f (x) (рис. 9). Эквидистантную к ней кривую можно получить по формуле f* (x) = f (x) - r / cos[a] или f,(x) = f (x)-r• V1 + [f‘(x)]2 .

Обобщенная сила сопротивления по возможному перемещению 8 х (равная силе трения R_x ( x ) , см. рис. 8, а ):

2 • M _c • 8a = - 2 • р • N ( x ) • 8 1 = - 2 • р • N ( x ) • 8 x = - 2 • р • N ( x )

8 x              r • 8 x          r • 8 x • cos(a)       r • cos(a)

где M _c - момент сопротивления, M _c = р • N ( x ); р - коэффициент трения качения; N ( x ) = с •A 1 • cos(a); A 1 = f ( x ) - 1 ₀ - b .

Окончательно имеем

2    • р • с •(f (x)-10 - b) •cos(a)     2 • р • с •(f (x)-10 - b)

=- r •cos(a)                           r

Зная функцию fx ), определяемую по формуле (6), находим мощность сил сопротивления на участке действия перегрузки к 1 • mg .

2J' R x _dx ₂ р^ с Ч ^f ( x )^-^ ^- b ) _dx

N 1 = ^-J°Tr^_=--------Tr -----------’                 ^<10 )

где r = 0,1 м; р - коэффициент трения качения: закаленная сталь по закаленной стали, р « 10 ^{- 6} м; x 10 = 10 м; T - время движения по правой ветви силовой характеристики

(см. рис. 1, б ), T 1 = Т эф = 2 с (см. рис. 6, а ).

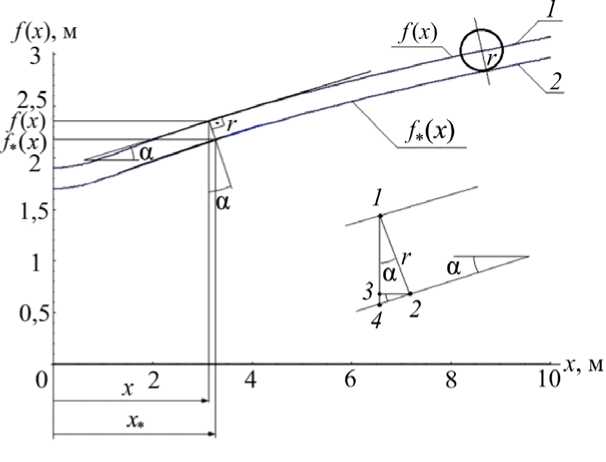
Рис. 9. Формы направляющих ( f ( x ); f , ( x )) для части силовой характеристики ( F 1 (x ) = к₁₀ -m-g 4h[ x ] + к ₂₀ • m ^ g • th[0,8 x ] ), полученные по формулам (6) и (7); 1 ₀ = 0,5 м; L ₀ = 3,4 м; b = 0,4 м; с = 5000 H/м; r = 0,1 м

Интеграл     2⋅µ⋅с ⋅(f(x)-l0 -b)dx ≈ 1,47 Дж был определен численным

0r интегрированием, т.е. мощность сил сопротивления невелика, даже учитывая коэффициент полезного действия и то, что движение осуществляется только по левой ветви силовой характеристики (мощность некоторых центрифуг, используемых для тренировки космонавтов, составляет десятки мегаватт).

Искусственную силу тяжести применяют и в земных условиях в качестве гравитационной терапии [6], для чего используют центрифуги малого радиуса действия со всеми вышеописанными принципиальными недостатками. Колебательная система, имеющая силовую характеристику, изображенную на рис. 1, б , предполагается перспективной для использования ее при гравитационной терапии.

Определим аналитически функцию f ( x ) для вертикальной системы, изображенной на рис. 7, а , имеющей силовую характеристику, изображенную на рис. 1, б , без учета участка перехода ВС . Рассмотрим движение по участкам. На участке АВ движение описывается следующим дифференциальным уравнением:

mX I = mg .

Начальные условия для этого дифференциального уравнения x 0 = x ₁₀; X ₀ = 0.

На участке CD колебания описываются дифференциальным уравнением mXII = -kmg + mg,                             (12)

где kmg – модуль восстанавливающей силы, действующей на объект массой m (кабина с человеком); k – задаваемый коэффициент.

Начальные условия для дифференциального уравнения (12): ^x о = 0; X = V 2 • g • x_to .

При решении дифференциальных уравнений (11), (12) получены зависимости, представленные на рис. 10.

Для предлагаемых систем, имеющих заданные силовые характеристики, в качестве упругого элемента можно использовать не только пружины, но и пневмопружины (см. рис. 8, б ). Для определения функции f ( x ) здесь можно воспользоваться следующим соотношением:

∆ lx

- ∫ F _пн( ∆ l ) d ∆ l = ∫ F ( x ) dx ,                             (13)

p⋅S⋅Hn где F = 0        – сила упругости пневмопружины; n – показатель политропы,

(H* -∆l)n n = 1; 3 [9]; H* – осевая длина цилиндра пневмопружины в несжатом состоянии; S – площадь поршня пневмопружины; p0 – начальное давление в пневмопружине; L0 – длина пневмопружины в несжатом состоянии (см. рис. 8, б); ∆l=2(L0/2- f(x))=L0-2⋅ f(x); d∆l = -2df(x).

Уравнение (13) можно переписать следующим образом:

-

^{∆ lp 0 ⋅ S ⋅ H * n} d ∆ l = ^xF ( x ) dx .

^∫ 0 ( H * -∆ l ) ^{n       ∫} 0

Л с

б

в

г

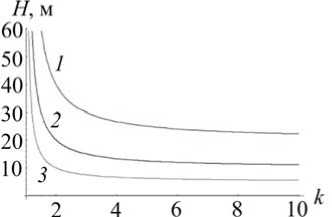
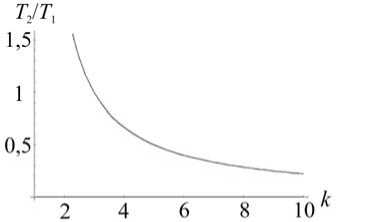
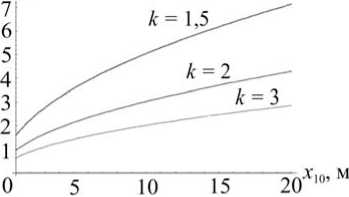
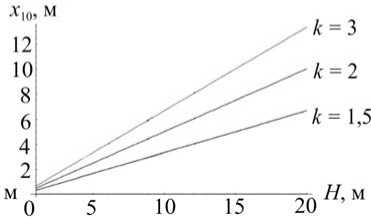
Рис. 10. Зависимости, полученные решением дифференциальных уравнений (11),

(12): а

k зависимость величины H = x10 •    , определяющей габариты к -1

конструкции (см. рис. 1, б ; рис. 7, а ), от коэффициента перегрузки к ; б -

T / T = — от к ; в - T = ^x" + ²¹ к - 1          g g

² • У² • g • x 10 g • ^{( к -} 1)

от x 10 ; г - x ₁₀ =

H • ( к - 1) k

от H

Определим f(x) для случая, когда F(x) = R^mg, где к - коэффициент, определяющий величину заданной постоянной силы F(x). Проинтегрировав уравнение (14), получим p0 • S • H*n (H* - L0 + 2 • f (x))1-n - p0 • S • H* = к • mgx • (n -1). Окончательно имеем f (x) = 0,5 • ((

к • m • g • x • (n -1)

p ₀ • S • H * n

+ H * ^{1 - n} )^{1/(1 - n} ) + L ₀ - H * ).

С учетом радиуса роликов r (см. рис. 8, б ) функцию f . ( x ) можно определить по формуле, аналогичной формуле (7):

f * ( x ) = f ( x ) + r • V 1 + [ f '( x )]². (16)

Для пропорционального изменения постоянной восстанавливающей силы F ( x ) в системе, изображенной на рис. 8, а , достаточно поменять пружину с одним коэффициентом жесткости на пружину с другим коэффициентом жесткости (6); в системе, изображенной на рис. 8, б , достаточно изменить начальное давление в пневмопружине (16).

Для систем, схема которых изображена на рис. 7, б , предлагается использовать упругие шарниры с заданной угловой силовой характеристикой M (ф) (см. рис. 7, б ; рис. 11), которая подбирается таким образом, чтобы получить заданные линейные силовые характеристики F ( x ) (см. рис. 1).

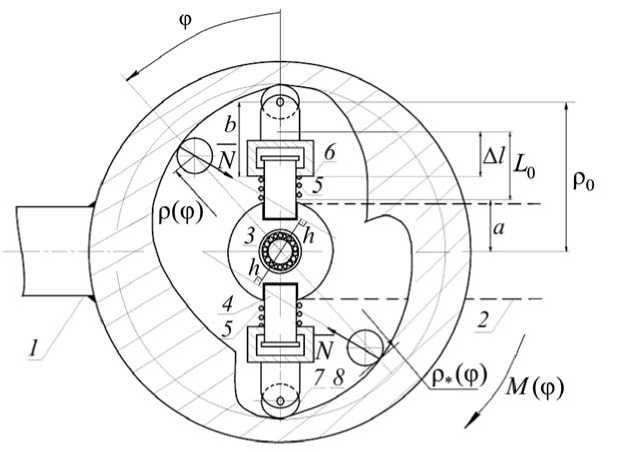
Рис. 11. Схема упругого шарнира с заданной угловой силовой характеристикой M (φ)

Стержень 1 соединен со стержнем 2 через упругую связь. В центре шарнира расположен подшипник 3, внутреннее кольцо которого связано с одной частью шарнира, наружное – с другой, в которой расположены направляющие пружин 4. На них насажены пружины 5. С пружинами контактируют держатели роликов 6. Сами ролики 7 перемещаются по направляющим 8 заданной формы. Реакции N не проходят через центр шарнира и создают момент M^ (ф) = 2 • N • h (от двух реакций - система симметрична).

Пусть задана угловая силовая характеристика M ^ (ф) = 2 M (ф). Требуется определить форму направляющей 8 для этой характеристики. Трение не учитывается.

При повороте одной части шарнира по отношению к другой на угол φ (от вертикали, см. рис. 11) момент сопротивления системы для одной пружины определяется по следующей формуле (радиус ролика 7 принят равным нулю):

M (ф) = —

дП дф ,

с 2

где П - потенциальная энергия одной пружины, П = 2 (Al) , Al - изменение пружины при повороте для данной схемы упругого шарнира, Al = (a + L0 + b - p).

Формулу (17) можно переписать:

M (ф) = c • (a + L + b - p) d-, dφ длины

где a , b – постоянные величины (см. рис. 11); L ₀ – длина ненапряженной пружины; ρ – расстояние от центра роликов 7 до центра шарнира.

Теперь, задавая функцию M (φ) и решая дифференциальное уравнение (18), можно получить зависимость ρ(φ) . При учете радиуса r ролика 7 (см. рис. 11) необходимо построить эквидистантные к данным кривые.

Рассмотрим пример. Требуется подобрать такую угловую силовую характеристику M (φ) упругого шарнира (рис. 12, а ), чтобы общая силовая характеристика системы была заданной: F(y ) = 1000 Н - const ( l = 0,5 м).

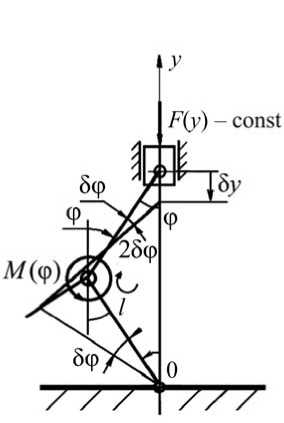
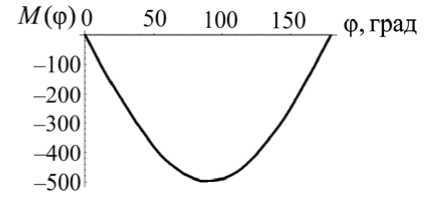
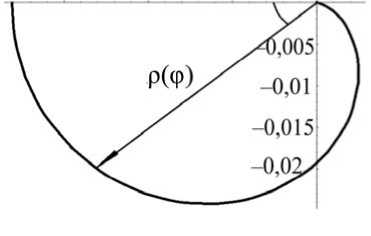
Рис. 12. Использование упругих шарниров с заданной угловой силовой характеристикой M (φ) для создания искусственной силы тяжести; F = 1000 H; l = 0,5 м; с = 100 000 Н/м: а - схема использования двух упругих шарниров с заданными угловыми характеристиками; б – угловые характеристики шарнира; в – форма направляющих для упругого элемента пружины

Решение выполним, приравняв к нулю обобщенную силу по возможному перемещению δ y :

_ F • 5 у - M • 25ф _

Q ⁵ у =       5 у      "

Выразим 5ф через 5у (5ф = 5у / 2l sin а ) и подставим в уравнение (19). Сократив на 5у, получим M = F • l • sin ф (рис. 12, б). Теперь можно определить р(ф) по формуле (18), пусть a = 0,03 м; L0 = 0,05 м; b = 0,04 м; р0 = 0,1 м . Подставим в формулу (18) выражение M (ф) / 2: F • l • sin ф/2 = c •( a + L 0 + b - р) —. Решая последнее dφ дифференциальное уравнение, получим р = 0,12 ± 7 (0,12)2 + 500 • (1 + cos ф)/ c.

На рис. 12, в показана зависимость ρ(φ), построенная по формуле (20) (угол φ изменяется от 0 до 180 град; с = 100 000 Н/м).

Заключение

Идея использовать повышенные перегрузки во время длительных космических полетов для профилактики вредного влияния на организм невесомости может оказаться очень перспективной, а предложенные в статье для этой цели колебательные системы с квазинулевой жесткостью (квазипостоянной восстанавливающей силой) на базе упругого элемента, перемещающегося между направляющими заданной формы, весьма эффективными.

Для более полного понимания данной проблемы, нахождения параметров заданных колебаний необходима серия экспериментов как в земных условиях, так и в космосе.

Предлагаемые колебательные системы могут найти широкое применение и в гравитационной терапии как более перспективные и дешевые по отношению к известным центрифугам.

Благодарности

Работа выполнена при поддержке гранта Российского фонда фундаментальных исследований (№ 12-08-97026-р_поволжье_а).