Создание конечно-элементных моделей частей скелета человека с приложениями к задаче исследования собственных колебаний

Успехи современной медицины в значительной части обусловлены использованием в медицинских исследованиях достижений естественных наук. Одним из важнейших инструментов извлечения новых научных знаний является математическое моделирование, открывающее перспективы для изучения многообразных связанных физико-механических процессов в органах человека. На основе математических моделей становится возможным точно и своевременно выявлять патологии, а также определять оптимальные способы медицинского воздействия и прогнозировать их последствия.

На первом этапе математического моделирования создаются трехмерные образы реальных фрагментов (в дальнейшем объектов) исследуемой системы. Для технической системы геометрический образ объекта формируется изначально, при описании ее структуры, и имеет вид чертежа. Поэтому воссоздать образ объекта в математической модели достаточно просто. Для этого применяются специальные программные средства, такие как CAD-системы [1], в которых граница исследуемого объекта представляется в виде совокупности границ стандартных геометрических фигур (плоскости, шара, эллипса, тела вращения), и параметры этих фигур заранее известны (например, для шара — это радиус и координаты его центра).

Трудность построения пространственных образов реальных живых организмов обусловлена тем, что в распоряжении исследователя нет «электронного чертежа» моделируемых органов. К тому же учет индивидуальных особенностей каждого конкретного организма еще больше осложняет задачу. Как правило, органы имеют сложные пространственные границы, которые невозможно построить с помощью стандартных CAD-операций и определить их параметры обычными для технических приложений средствами измерений.

Однако решение задач построения геометрических образов реальных органов стало возможным с появлением современных томографических устройств, таких как мультисрезовая рентгеновская и магниторезонансная томография [2]. К сожалению, цифровая информация, получаемая в процессе томографической съемки, не может быть непосредственно использована для построения конечномерного сеточного образа (например, такого как конечно-элементная сетка), определяющего пространственную геометрию органа. Томографические данные представляют собой картины распределения интенсивности измеряемых величин в последовательности плоских сечений исследуемого объекта (каждое сечение обладает привязкой к глобальной системе координат). Определенные диапазоны значений интенсивности соответствуют конкретным тканям органа (костям, мышцам и тому подобным).

В ранее опубликованной работе авторов [3] приведен алгоритм построения границ органов человека по данным томограмм, базирующийся на методе фронтального роста [4]. В основе метода лежит анализ образов плоских сечений реального органа и выделение в них областей с близкими значениями интенсивности регистрируемой величины. Объединение таких областей в последовательных сечениях

позволяет вычленить пространственные области с определенным диапазоном интенсивности, которые можно рассматривать как трехмерные образы структурных элементов человеческого органа.

Используемый алгоритм является итерационным. Первоначально исследуемая область представляется в виде совокупности подобластей — «областей роста». На каждой итерации к текущей области роста добавляются соседние участки, имеющие близкие значения интенсивности измеряемой величины. Процесс продолжается до тех пор, пока количество элементов, добавленных за итерацию, не станет равным нулю. Алгоритм позволяет получать замкнутые области, причем не только односвязные, но и многосвязные. Он обладает высокой скоростью и дает возможность выполнять декомпозицию томографического образа с целью выделения области, принадлежащей конкретной структуре организма. Отличительной особенностью этого алгоритма является то, что построенный на его основе геометрический образ реального объекта может использоваться для создания конечно-элементной модели, которая необходима для численного решения краевых задач, ставящих целью изучение физико-механических процессов, имеющих место в органах человека. Этот дискретный образ обладает универсальностью и может быть использован в различных коммерческих программных продуктах.

Следует отметить, что наряду с представленным алгоритмом существуют коммерческие программные продукты, реализующие построение геометрических образов на основе томограмм. К их числу относятся MIMIKS [5] и SIMPLWARE [6], но их алгоритмы не опубликованы.

В данной работе описанный выше алгоритм является одним из этапов процесса создания трехмерного конечно-элементного аналога реального органа человека. На первом этапе осуществляется сканирование на рентгеновском или магниторезонансном томографе. На втором этапе цифровые данные томографических измерений обрабатываются программой, которая формирует для каждого структурного элемента органа ограничивающую его трехмерную поверхность. Каждая такая поверхность представляется совокупностью плоских треугольных элементов. Затем поверхностная сетка экспортируется в блок генерации сеток программного комплекса ANSYS (ANSYS ICEM CFD), который формирует объемную тетраэдральную сетку с заданными параметрами разбиения для всего органа. Полученная трехмерная сетка может быть использована в большинстве вычислительных пакетов, открывая тем самым возможность постановки и решения задач исследования различных физико-механических процессов, происходящих в органах живых организмов.

В данной статье возможности подхода продемонстрированы на примере решения задачи нахождения характеристик собственных колебаний частей скелета человека. Одним из практических приложений этой задачи является вибромониторинг процесса заживления костей при переломах [7]. Однако в работе [7] геометрический образ большеберцовой кости создан на основе данных непосредственных измерений, проводимых на «неживом» образце, что ограничивает применение вибромониторинга в медицинской практике, поскольку созданный образ лишен уникальных особенностей живого организма. Результаты настоящего исследования, в отличие от [7], позволят создавать геометрические образы неинвазивным способом и учитывать при этом индивидуальные свойства органов

Приведенные ниже результаты базируются на материалах томографических исследований, представленных на сайте разработчиков программного обеспечения для расшифровки медицинских изображений в стандарте DICOM [8].

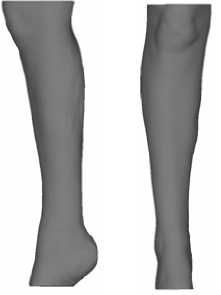
На рисунке 1 показаны результаты выделении пространственных областей, соответствующих мягким и костным тканям левой ноги человека. Информация о поверхностях структурных элементов большеберцовой кости, полученная согласно вышеописанному алгоритму, экспортировалась далее в блок генерации сеток программного комплекса ANSYS. Созданные с его помощью пространственные конечно-элементные образы большеберцовой кости, костей черепа и таза представлены на рисунках 2–4.

а

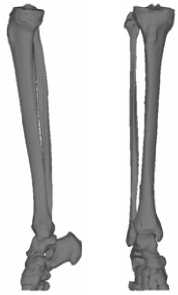
Рис. 1. Декомпозиция томографического образа ноги человека (вид сбоку и спереди): мягкие ткани ( a ); костные ткани ( б )

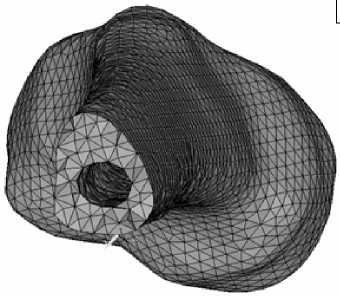
Рис. 2. Пространственный конечно-элементный образ большеберцовой кости человека ( а ); фрагмент ее верхней части ( б )

а

б

в

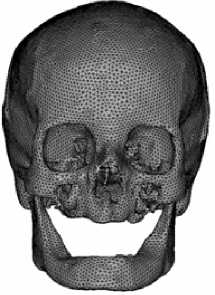
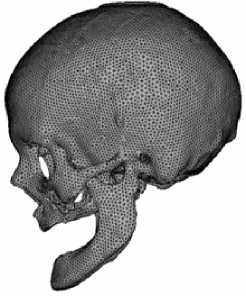
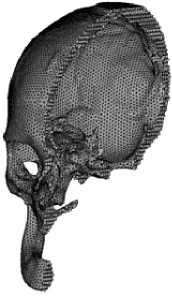
Рис. 3. Пространственный конечно-элементный образ костей черепа в трех видах: спереди ( а ), сбоку ( б ), в разрезе по плоскости симметрии ( в )

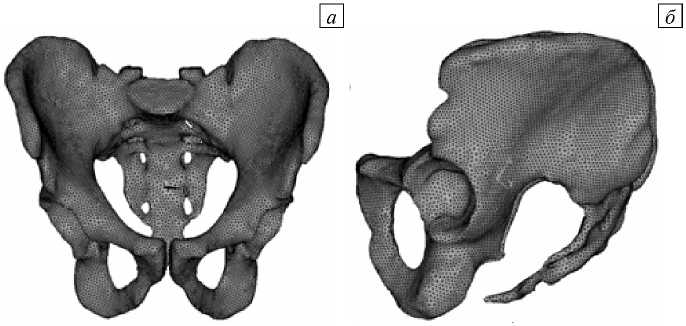
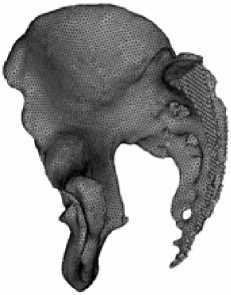
Рис. 4. Пространственный конечно-элементный образ костей таза в трех видах: спереди ( а ), сбоку ( б ), в разрезе по плоскости симметрии ( в )

в

Построенные пространственные конечно-элементные образы послужили основой для нахождения собственных форм и частот колебаний большеберцовой кости, костей черепа и таза человека. Постановка каждой из этих задач осуществлялась в рамках линейной теории упругости [9]. Соответствующие однородные краевые условия для каждой задачи описаны ниже. Численное решение находилось методом конечных элементов с использованием программного комплекса ANSYS. Во всех трех случаях костная ткань полагалась изотропной и упругой, и, в соответствии с [10], использовались следующие механические характеристики костной ткани: модуль Юнга E = 10 ГПа, коэффициент Пуассона v = 0,3, плотность р = 2400 кг/м³.

В постановке задачи для большеберцовой кости учитывалось допущение, что области контакта кости с голеностопным ( А ) и коленным ( Б ) суставами неподвижны (Рис. 5, а ). Анализ результатов вычислений позволил установить, что основное смещение, согласно первой форме колебаний, происходит в направлении нормали к боковой плоскости ноги (см. Рис. 5, б ) с собственной частотой 370 Гц, а согласно второй — в направлении нормали к фронтальной плоскости ноги с частотой 446 Гц. Из этого, в частности, следует, что эффективная жесткость голени на изгиб во фронтальном направлении больше, чем в боковом.

а

Рис. 5. Большеберцовая кость: схема закрепления ( а ); первая собственная форма колебаний ( б )

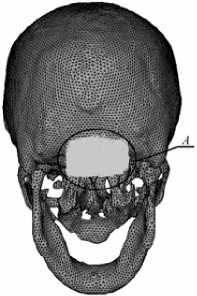
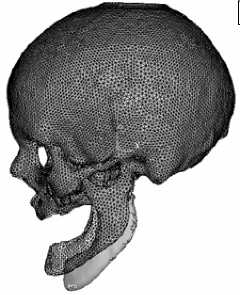
При постановке задачи определения форм собственных колебаний черепа его основание считалось жестко закрепленным и в височно-нижнечелюстном суставе исключалась возможность свободного относительного смещения. На рисунке 6, а показан конечно-элементный образ черепа и выделено место контакта основания черепа с позвоночником (область А). При первой форме колебаний (собственная частота 245 Гц) доминирующие смещения возникают в нижней челюсти (Рис. 6, б ) (деформированная зона показана серым цветом).

а

Рис. 6. Череп: конечно-элементный образ ( а ); первая форма колебаний ( б )

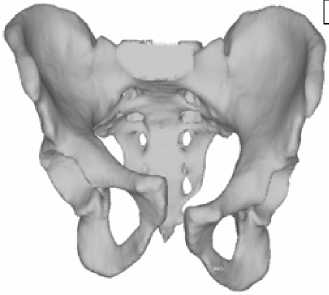
При получении форм собственных колебаний костей таза предполагалось, что в области сочленения таза с позвоночником (область А , Рис. 7, а ) выполняются условия жесткого закрепления. Первая форма колебаний костей таза (частота 171 Гц) представлена на рисунке 7, б.

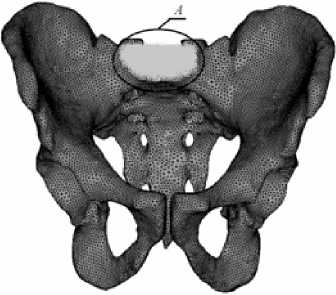
Рис. 7. Кости таза: конечно-элементный образ ( а ); первая форма колебаний ( б )

Выводы

В работе продемонстрированы возможности разработанного подхода к созданию конечно-элементных образов органов реального человека на основании результатов томографических измерений. Построены конечно-элементные образы костей голени, черепа и таза, и на их основе с помощью метода конечных элементов найдены собственные формы и частоты колебаний. Выявлены области, в которых эти органы испытывают наибольшие смещения на первой форме колебаний.

Конечно-элементные образы могут быть использованы при решении других физико-механических задач, таких как моделирование процессов разрушения кости, совместного деформирования систем протезирования и костной ткани и тому подобных.

Работа выполнена при финансовой поддержке РФФИ (проект № 11–01–96016–р_Урал_а), Междисциплинарного проекта УрО РАН № 12-М-14-2009 «Виртуальное сердце: интегративные компьютерные математические модели».