Создание программы для нахождения аппроксимирующей функции полученных экспериментальных результатов методом наименьших квадратов

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 378.4:004.421                                   

При решении технико-экономических задач часто бывает необходимо определить математические зависимости между различными параметрами, характерными для данной задачи [1–3].

Исходной информацией, определяющей эти зависимости, является физический эксперимент или экономические показатели. В обоих случаях мы располагаем либо табличные данные, либо точки на графике. Предположим, что есть зависимость P i , полученная с дискретными значениями Z i . Значения P i получены из эксперимента с некоторыми погрешностями. Необходимо найти зависимость P=f (Z) (Рисунок 1).

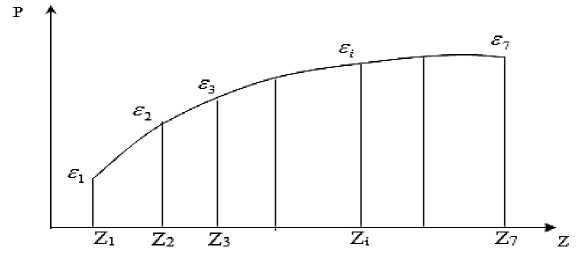
Рисунок 1. График зависимость P i , полученная при дискретных значениях Z i

Поскольку, что P=f (Z) имеет явно выраженную нелинейную зависимость, мы запишем уравнение кривой второго порядка.

p=x0 + xz+x2z 2

В этом уравнении X 0 , X 1 , X 2 , неизвестные пока коэффициенты. Чтобы найти эти коэффициенты, запишем зависимость вида (1.1) для всех доступных значений P i .

p = x0 + xz + xz 2

p = x0 + xz2 + xz2

Pi = X 0 + X1 Zi + X 2 Z*

p = x0 + xz7 + xz

Получена система из 7 уравнений с 3 неизвестными. Необходимо таким методом найти, X 0 , X 1 , X 2 чтобы зависимость (1) наилучшим образом описывала результаты, представленные на графике.

Для нахождения трех неизвестных, чтобы решить систему из 7 уравнений. Если мы отбросим какие-либо 4 лишних уравнений, мы найдем значения неизвестных, не считая эти уравнения отброшенными. С другой стороны, система (2) может быть несовместной, то есть при решая ее, мы не можем получить тождества и, подставляя найденные значения неизвестных в системные уравнения, получаем разность между левой и правой частями.

Обозначим эти разницы в соответствии с номерами уравнений через f p £ 2 ... £ i ,..., £ 7 и будем называть их невязками. Невязка — это разница между аналитической зависимостью и значениями P i , указанными в качестве исходной информации в дискретных точках Z i .

Для того чтобы аналитическая зависимость результатов эксперимента наиболее полно отражала, будем минимизировать величину:

сс ) ®  |

S = S ^

i = 1

Невязки взяты в квадрат для того, чтобы любая невязка получалась с положительным знаком, при увеличении соотношений малых и больших невязок. Минимизация S будет выражать наилучшее приближение аналитической зависимости в экспериментальных точках (при заданной степени полинома). Общая формулировка задачи:

необходимо решить систему n -линейных уравнений с m неизвестными.

a 11 x 1 +a 12 x 2 +…+a 1j x j +…a 1m x m =b 1                                 (4)

a 21 x 1 +a 22 x 2 +…+a 2j x j +…a 2m x m =b 2

ai1x1+ ai2x2+…+aijxj +…aimxm =bi an1x1+an2x2+…+anjxj+…anmxm=bn

Запишем i -тое уравнение в более компактном виде:

m

S a yxj = bi j=1

Тогда

n    nm

S = S J = S (S ajXj- bi)

i = 1              i = 1    j = 1

Для минимизации S возьмем частные производные каждой переменной x j из этого значения и равняем его 0.

nm

— = 2E(Ea.x, -b)a, ij j           i ij dxj       i=1 J=1

---= 0, отсюда:

dXj

nm

S ⁽ S ^a J ^x j ^{- b}) a = ⁰, i = 1    J = 1

Таких уравнений будет много, так как неизвестные x j и получим систему n-линейных алгебраических уравнений с n неизвестными, которые можно решить методом исключения с выделением главного элемента.

Обзор программного обеспечения

Реализация метода наименьших квадратов в среде Delphi 10. После запуска программы появляется окно, показанное на Рисунке 2.

Т. 7. №12. 2021

Рисунок 2. Главное окно программы

При нажатии кнопки «Открыть» появится диалоговое окно открытия файла с исходным данными (Рисунок 3).

Рисунок 3. Выбор файла с экспериментальными данными

При выборе файла появляется форма (Рисунок 4).

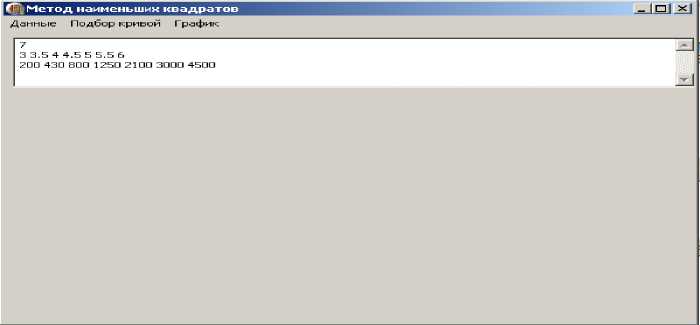
Рисунок 4. Показ исходные данные

Здесь в верхнем окне содержатся исходные данные, т. е. количество точек измерений и сами значения в выбранных точках. Нажимаем на кнопку «Подбор кривой» и «Расчет», (Рисунок 5).

Рисунок 5. Расчет графика

Теперь после нажатия на кнопку «График» и «Подобранная кривая» получаем графики экспериментальных данных и подобранной кривой (Рисунок 6).

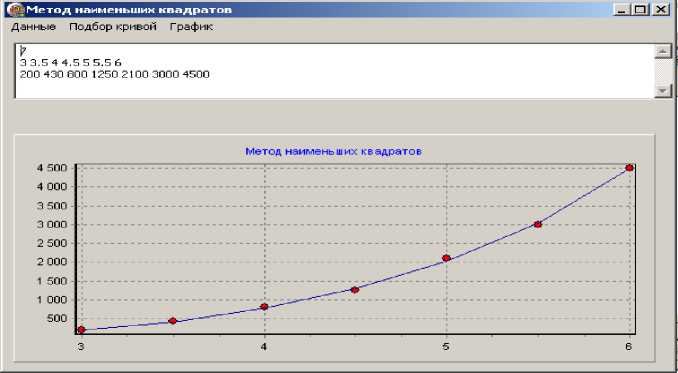
Рисунок 6. Графики экспериментальных данных и подобранной кривой

Как видим, график экспериментальных данных и подобранной кривой практически совпадают.

Заключение

Рассмотрены одним из сложнейших разделов математики — обработка экспериментальных данных. В статье реализованы методики обучения методом наименьших квадратов, сопутствующий ему и возникающий при реализации метода наименьших квадратов и методы решения системы линейных алгебраических уравнений.