Создатель теории реактивного движения. 2 (к 155-летию со дня рождения И. В. Мещерского)

Предисловие

Иван Всеволодович Мещерский – выдающийся российский учёный-механик и педагог высшей школы, представитель Петербургской научной школы классической механики, ученик выдающегося российского учёного и педагога, ординарного профессора Императорского Санкт-Петербургского университета по кафедре прикладной математики Д.К. Бобылёва (1842-1917).

В своих известных основополагающих трудах [1–4] И.В. Мещерский заложил теоретические основы динамики материальной точки переменной массы и механических систем переменного (изменяемого) состава. Он является основоположником принципиально нового научного направления в теоретической (рациональной) механике – динамики массоизменяемых и конфигурационно изменяемых механических объектов, создателем основ системной фундаментальной теории реактивного движения.

В работе [5] приведены некоторые достижения И.В. Мещерского в теории реактивного движения, а также вклад его предшественников в эту область. В настоящей статье продолжено рассмотрение вопросов, поставленных в статье [5].

В своих сочинениях [6, 7] К.Э. Циолковский приводит решения задач о поступательном прямолинейном движении ракеты, которые в учебной литературе называются "задачами Циолковского" [8–11].

Решение первой задачи ракетодинамики

В сочинении "Исследование мировых пространств реактивными приборами" [6] Циолковский (он, по-видимому, не разделял понятия "приборы" и "аппараты") рассматривает задачу о поступательном прямолинейном движении ракеты (которую он называет и "снарядом" и "ядром") на активном участке траектории. В разделе "Ракета в среде, свободной от тяжести и атмосферы" Циолковский рассматривает движение, которое, по предположению, совершается вне поля тяготения в среде без сопротивления согласно уравнению dV (M 1 + M) = V1 dM.        (1)

В равенстве (1) обозначено (обозначения Циолковского [6]): V - "скорость движения ракеты вместе с оставшимися нетронутыми взрывчатыми материалами"; M1 – "масса снаряда со всем содержимым, кроме запаса взрывчатых веществ" (ВВ) [запаса топлива ракеты]; M – "переменная масса ВВ, остав- шихся не взорванными в снаряде в данный момент" (Циолковский не различал понятия "взрыв" и "горение"); V1 – "постоянная относительно ракеты скорость бесконечно малого отброска dM взрывчатого вещества".

В результате интегрирования уравнения (1) Циолковский получает соотношение [6]

V = In

f M + M

^ M 1 + M

и при этом замечает: "Знаки обеих частей уравнения [(2)] обратные, так как скорости V, V 1 противоположны по направлению" [6]¹. В уравнении (2) обозначено: M 2 – "полная масса взрывчатых веществ", M 1 + M 2 – "полная масса ракеты при начале взрыва" (т.е. масса M 0

ракеты в начальной точке её активного участка траектории) [обозначения Циолковского].

Из равенства (2) при M = 0 следует "наибольшая скорость снаряда" V

M

V = In 1 + M 2 I .

V 1

I M 1

О второй задаче ракетодинамики

В разделе сочинения [6] "Ракета под влиянием тяжести. Вертикальное поднятие" Циолковский рассматривает вторую задачу ракетодинамики, для решения которой он применяет не аналитический аппарат теории обыкновенных дифференциальных уравнений (как это сделано в работе И.В. Мещерского [2]), а эвристические предложения, достоверность которых он должным образом не аргументирует. В частности, величина высоты максимального поднятия ракеты h в расчётах Циолковского не представлена в зависимости от конкретного вида закона изменения величины массы ракеты от времени. Она выражена равенством [6]

h = a g 1 2 ,

2, которое не нуждается в комментариях как относящееся к школьному курсу элементарной физики.

Отсюда не имеется возможности сопоставить полученные Циолковским результаты с соответствующими результатами И.В. Мещерского (полученными аналитическим методом), что является предметом настоящей статьи.

В связи с этим следует отметить характерную особенность решения Циолковским задач ракетодинамики: ни в одной из рассмотренных им задач он не применял понятия "закон изменения величины массы" для материальной точки переменной массы и не приводил каких-либо его конкретных аналитических выражений.

В частности, для нахождения соотношений (2), (3) такого закона не требуется, но для получения величины наибольшего поднятия ракеты в поле силы тяжести или величины наибольшего пройденного расстояния на активном участке траектории вне поля тяжести введение такого закона при использовании аналитического метода существенно необходимо. При этом лишь интегрирование уравнений движения ракеты в задачах ракето-динамики может привести к достоверному конечному результату.

В силу отмеченного содержание упомянутого раздела сочинения Циолковского здесь не рассматривается.

О гипотезе имени Циолковского

В своём сочинении [6] Циолковский в разделе "Ракета в среде, свободной от тяжести и атмосферы" при интегрировании уравнения (1) принимает ограничение V1 = const, имеющее гипотетический характер, которое в ряде литературных источников (указанных ниже) было названо гипотезой Циолковского. Авторы, которые ввели это название и неоднократно его тиражировали, по-видимому, считали, что такое предположение впервые было опубликовано Циолковским.

Сам Циолковский в своём сочинении в связи с этой гипотезой писал: "Я хочу сказать, что относительная скорость V 1 вырывающихся элементов [ dM ], при одинаковых условиях взрыва, одна и та же во всё время взрывания, – на основании закона относительных движений…" [6]².

Очевидно, что при этом предположении уравнение движения (1) легко интегрируется в конечном виде. Однако в случае переменной величины V 1 ( t ) интегрирование этого уравнения в конечном виде уже требует задания явных видов гладких функций M ( t ), V 1 ( t ); о конкретных видах этих функций Циолковский, по-видимому, ничего не знал.

Достижения Мещерскогопод именем Циолковского

И.В. Мещерский публиковал свои основополагающие работы [2–4] в период с 1897-го по 1904-й гг. Его работа "Динамика точки переменной массы" [2] и одноимённая магистерская диссертация, защищённая в Петербургском университете, "явилась первым крупным исследованием, посвящённым целиком динамике систем переменного состава" [12]; она "является наилучшим достижением его научного творчества" и "составляет надёжный теоретический фундамент современной ракетодинамики" [13, c. 25]. "В этой фундаментальной работе, кроме открытия исходных … уравнений, рассмотрено большое число оригинальных частных задач и указаны общие методы" [9, c. 237].

Как "замечательно" высказался один из поклонников Циолковского: "Теория прямолинейных движений ракет была в значительной степени создана трудами знаменитого деятеля русской науки К.Э. Циолковского, хотя в уравнениях Мещерского было всё необходимое для создания вполне законченной динамики ракет" [13, c. 21].

К.Э. Циолковский публиковал свои сочинения по ракетодинамике [6, 7] в период с 1903-го по 1926-й гг. Первая его публикация [6] появилась в 1903 г., через 6 лет после опубликования работы И.В. Мещерского [2].

Таким образом, даты публикации обоих авторов по одним и тем же вопросам разделены указанным временн ы м интервалом, позволяющим достоверно установить хронологию появления их результатов.

Решение задач ракетодинамики

Поступательное прямолинейное движении ракеты на активном участке её траектории моделируются прямолинейным движением точки переменной массы под действием реактивной силы. Эта модель применена в простейших задачах ракетодинамики, относящихся к движению точки вне поля тяготения и в однородном поле силы тяжести.

Первоначальная постановка и решение такого рода задачи в однородном поле тяготения, согласно исследованиям Г.К. Михайлова [12], принадлежит У. Муру [14] (1810, 1811), [15] (1813), а также П.Г. Тейту и У.Дж. Стилу [16]3 (1856). Они являются историческими предшественниками глубоких научных исследований И.В. Мещерского в этой области.

В работе [2, c. 113-115] (1897) И.В. Мещерским рассмотрена задача "Восходящее движение ракеты" в следующей постановке: "Определить восходящее вертикальное движение точки переменной массы M, на которую, кроме силы тяжести, действует [переменная] сила … p, направленная по вертикали вверх, и сопротивление среды R ( x ), ... [и предполагается], что [относительная скорость V r ] направлена по вертикали вниз и … [является переменной величиной]". И.В. Мещерский, составив уравнение движения точки, интегрирует его в конечном виде в элементарных функциях для линейных законов сопротивления среды и величины массы точки как функции времени. В результате он определяет явные зависимости вида x ( t ) и x ( t ). Таким образом, здесь полностью решается вторая задача ракетодинамики в указанной постановке.

Помимо данной, И.В. Мещерским в этой же работе ставится и решается другая задача ракетодинамики, приведённая ниже.

Лишь в 1903 г. было опубликовано сочинение Циолковского [6]. Тем не менее, в ряде источников, в частности в учебниках [8, с. 24-31; 10, с. 50-52; 11, с. 555-558] и других (например, [9, с. 207, 214]) упомянутые задачи ракетодинамики названы первой и второй задачами Циолковского. Это означает, что авторы указанных публикаций считают Циолковского первооткрывателем, обладателем приоритета, впервые сформулировавшим и решившим простейшие задачи ракетодинамики.

Однако исторические факты подтверждают первенство в этом вопросе упомянутых английских авторов, представителей Кембриджской научной школы, и И.В. Мещерского, поставившего и решившего вторую задачу ракетодинамики при более общих условиях, чем в постановке Циолковского.

Циолковским в публикации [6] (1903) получена формула (2), входящая в решение первой задачи ракетодинамики, для поступательного прямолинейного движения ракеты в случае, при котором относительная скорость истечения продуктов сгорания топлива постоянна.

Подобная задача в более общей постановке была решена И.В. Мещерским в работе [2, c. 149]. Им рассмотрен случай движения, при котором "масса тяжёлой точки выражается какою-либо функцией времени, положения точки и длины пройденного пути, а … [ V r ] остаётся постоянною по величине и направлению": M = M ( t , r , s ), V r = const (движение точки в общем случае – криволинейное).

В этой задаче И.В. Мещерским для построенных им уравнений движения точки в пустоте получен первый интеграл [2, c. 150]

• x c ( t , r , s ) = X o + V r In M ( t , r , s ), (4) где принято M (0, 0,0) = M 0 = 1.

Соотношение (4) определяет проекцию скорости точки на ось координат Ox и по виду тождественно совпадает с соответствующей формулой, входящей в решение первой задачи ракетодинамики [11]. Формула (2), полученная Циолковским [6] в 1903 г., идентична соотношению (4) с точностью до аддитивно входящей в него начальной скорости x ₀.

Равенство (2) в изданиях [8, 9] названо формулой Циолковского. В книге [8] отмечается: "Формула

• V = V 0 + V r ln M^ (5) 0 r M

была впервые исследована К.Э. Циолковским и носит название формулы Циолковского" (c. 25).4

Это утверждение противоречит исторической хронике открытия зависимости (5), полученной в результате решения задачи, являющейся частным случаем упомянутой выше более общей задачи И.В. Мещерского. Этот исторический факт хорошо известен и неоднократно отмечался в литературных источниках, однако в историческом аспекте, вопреки очевидности, фактически неоднократно игнорировался [17].

Всё это даёт основание считать, что первооткрывателем закона изменения скорости точки в формах (4), (5), имеющим право на приоритет, является автор работы [2] – И.В. Мещерский [17].

О гипотезе постоянности относительной скорости отделения рабочего тела

Эта гипотеза формулируется в сочинении Циолковского [6] (1903), где он пишет: "Я хочу сказать, что относительная скорость V 1 вырывающихся [из ракеты] элементов [рабочего тела], при одинаковых условиях взрыва, одна и та же во всё время взрывания, – на основании закона относительных движений". И далее: " dM есть бесконечно малый отбросок взрывчатого вещества, вырывающегося … с постоянную относительно ракеты скоростью V 1 ".

В другом издании [7, с. 28] (1926) Циолковский пишет: "в основу теории ракеты надо принять постоянную относительную скорость частиц отброса". При этом почему именно " надо принять " (если это действительно требуется) никак не обосновывается.

Этот постулат в источниках [8, c. 20, 28, 29, 70, 171], [9, c. 207], [18, c. 339], [19, c. 167] и других публикациях назван " гипотезой Циолковского ", оставляя тем самым приоритет введения этой гипотезы в задачах ракетоди-намики за Циолковским.

Однако ещё в XIX в. английскими авторами У. Муром в статьях [14] (1810–1811) и трактате [15] (1813), а также в трактате П.Г. Тейта и У.Дж. Стила [16] (1856), это предположение было применено в ряде решённых ими задач. Так, например, в решении задачи о вертикальном восходящем движении ракеты в однородном поле силы тяжести ( вторая задача ракетодинамики ) [16], представленном формулами

м

[V m ] = V 1П — - M '

g (1 - ML 1 e t M J ,

[ h ] = V- l ln —I + V 1 1 - ^m 2g \ M')   e

M'

M

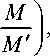
величина V – постоянная относительная скорость отделения рабочего тела. При этом Г.К. Михайлов в статье [12, с. 44] отмечает: "В разработанной … У. Муром [15] теории движения ракет также принималась постоянной скорость выгорания горючего материала в ракете".

Помимо указанных выше авторов, эту гипотезу в своей работе неоднократно применяет И.В. Мещерский [2]. Это сделано, в частности, в следующих задачах: о восходящем вертикальном движении ракеты (гл. 3, с. 114); о движении точки в однородном поле силы тяжести и сплошной среде с сопротивлением (гл. 6, с. 149); о движении точки в поле центральной силы, где относительная скорость отсоединения рабочего тела сохраняет постоянное направление (гл. 7, с. 168).

Все эти случаи применения данного постулата в задачах ракетодинамики опубликованы И.В. Мещерским за шесть лет до издания сочинения Циолковского [6]. При этом в последнем принят лишь частный случай данной гипотезы – постоянность скорости V r только по модулю, что характерно для прямолинейного движения частиц рабочего тела.

Из всего отмеченного следует, что приписывать Циолковскому авторское первенство в применении указанной гипотезы и называть её его именем нет оснований [17].

Мифотворчество как извращение истории науки

В 30-е гг. XX в. в нашей стране была развёрнута кампания по идеологизации и огосударствлению науки, подчинению её "целям и задачам коммунистического строительства". В связи с этим, исполнительной властью была дана установка о пересмотре некоторых положений исторической науки, в том числе и истории развития механики. Было выдвинуто требование о приоритетном оценивании достижений отечественной науки, российских и советских учёных в противовес "буржуазной науке Запада", основанной на "ложных идеалистических философских учениях". От деятелей науки настоятельно требовалось неус- танно возвеличивать в научных трудах, общественной печати и других средствах массовой информации достижения российских и советских учёных, не считаясь с реальной исторической правдой.

В русло этой кампании были вовлечены творения Мещерского и Циолковского: в соответствии с определённым идеологическим заказом была произведена переоценка научных достижений обоих авторов согласно выдвинутым установкам. Подход к этому был чисто политизированный и классовый: Мещерский – "буржуазный специалист" из "старорежимных", "социально чуждый элемент", бывший действительный статский советник, не вполне разделявший принципы коммунистической идеологии. А Циолковский - "деятель из народа", вполне разделявший и одобрявший политику "подлинных руководителей прогресса человеческой культуры"5.

Признавая фундаментальность научных достижений Мещерского, автор публикаций [9, 13] отмечает: "в уравнениях Мещерского было всё необходимое для создания вполне законченной [теории] динамики ракет" [9, c. 241; 13, c. 21]. Вместе с тем, далее он пишет: "Заметим, что на с. 121 диссертации И.В. Мещерского среди формул (3)⁶ имеется формула Циолковского для случая движения в однородном поле силы тяжести. Однако никакого анализа этой формулы диссертация Мещерского не содержит" [9, c. 241].

По логике этого автора выходит, что первоначально данную формулу получил (и что важно – в более общем виде) Мещерский, а впоследствии она стала называться (кстати, с участием этого же автора) формулой Циолковского.

Неуместное замечание автора приведённой цитаты по поводу отсутствия "анализа" формулы Мещерского с именем Циолковского" [формула (2)], не выдерживает никакой критики.

Действительно, Мещерский в работе [2] не ставил целью поиск её применения в области ракетодинамики и, следовательно, не должен был проводить какого-либо анализа с этой целью. Такой подход Мещерского является вполне естественным и логичным как подход к разработке любой естественнонаучной проблемы. Это, однако, не помешало ему рассмотреть в своей работе ряд конкретных примеров применения построенной им теории, а в последующих работах – и примеры технических применений [17].

Преуменьшение достижений И.В. Мещерского в теории реактивного движения

Фальсификации исторических фактов научных достижений, принижающие научные заслуги И.В. Мещерского как первооткрывателя в области теории реактивного движения, продолжительное время массово тиражировались в отечественных изданиях под видом истинных исторических реалий. Они внесли определённый вклад в мифологизацию истории научных открытий, порождённую кампанией политизации науки.

Подобного рода искажений достаточно много. Так, например, в публикации [20] отмечено, что И.В. Мещерский, "занимаясь чистой наукой, прошёл мимо грандиозных перспектив, открываемых этими формулами перед ракетной техникой" [20, c. 146]. В других публикациях, в частности, отмечалось, что Циолковский "свою формулу" получил применительно к движению ракет, а Мещерский, якобы, лишь для некоторого абстрактного объекта. Эти утверждения несостоятельны по ряду причин.

Действительно, в разделе "Предмет рассуждения работы" своей диссертации [2] И.В. Мещерский писал: "Глава 3 содержит задачи о прямолинейном движении точки переменной массы и, прежде всего, те, к которым мы приходим, рассматривая вертикальное движение горящей ракеты и привязного аэростата; затем … указан случай свободного аэростата, масса которого выражается … функцией расстояния его от земли …" (c. 43). В главе 1 рассмотрен пример "Вертикальное движение аэростата при выбрасывании балласта" (с. 57). Как отметил Е.Л. Николаи: "И.В. Мещерский первый дал строгое уравнение вертикального движения ракеты и показал, в каких частных случаях это уравнение можно исследовать до численного результата" [21].

Критики работ Мещерского выдвигают следующий аргумент: хотя Циолковскому и не принадлежит приоритет в решении задач ракетодинамики, однако он первым применил формулу для скорости ракеты к расчётам межпланетного полёта ракеты. Этот наивный аргумент не нуждается в комментариях, иначе, например, можно было бы обсуждать вопрос о первом в истории науки применении законов 10-тиричной или 7-миричной арифметики. Известно, что первичное применение кем-либо открытого закона в какой-либо области познания не является предметом приоритета.

Стремясь преуменьшить научные достижения И.В. Мещерского и поставить под сомнение его приоритет в решении задач ракето-динамики, его критики утверждают, что, оказывается, ещё "10 мая 1897 г. Циолковский вывел свою знаменитую формулу … А уже в 1898 г. он окончательно оформил свой труд [6]"7 (А.Г. Глухов, 1979). Однако вот что по этому поводу писал сам Циолковский в своей рукописи: "Я многое открыл, что было уже открыто ранее меня. … Молва и печать их [моих работ с открытиями, совершёнными ранее меня] распространяют иногда и без указания источников. Печатная дата – вот что решает спор о первенстве и значении учёного" [22, л. 1].

Продвижение идей И.В. Мещерского в теории реактивного движения

Научные идеи классиков науки не умирают вместе со смертью их творца. Они живут долгие годы, углубляя и развивая заложенные ими основы. Так произошло и с теорией реактивного движения, основанной И.В. Мещерским.

В связи со стремительным развитием реактивной техники после окончания Второй мировой войны теория реактивного движения обрела актуальность. Стали совершенствоваться конструкции реактивных систем и расширяться связанная с ними опытноконструкторская база. Наступило время применения научных достижений и идей И.В. Мещерского, время дальнейшего развития основанной им системной теории.

После издания труда [1] в научной печати появилось множество публикаций в этой области. Одной из них является статья [23], содержащая исследование движения высокоинтенсивной реактивной системы (РС), в динамику которой существенный вклад вносят вариационные силы. Эти силы возникают вследствие интенсивного нестационарного движения рабочего тела (РТ) относительно неизменяемой части (корпуса) РС. Для неин- тенсивных РС влияние вариационных сил пренебрежимо мало, а для РС, моделируемых тележкой Д.Е. Охоцимского8, оно бывает довольно значительным.

Пусть РС движется поступательно и прямолинейно в направлении оси Ox; x ( t ) – координата центра тяжести C 0 системы без РТ, а M 0 – масса этой РС; M ( t ) - масса РС, содержащей РТ, с центром тяжести С; l ( t ) – расстояние от точки С 0 до выходного сечения сопла РС. Пусть далее задана функция f ( t ) – координата точки С относительно С 0 как величина, зависящая от конфигурации полости, содержащей жидкое РТ, и закона его вытекания из РС.

Рассмотрим случай движения РС, для которого l = const, f(t) ≡ 0, а проекция на ось Ox относительной скорости вытекающего РТ есть u = const ≠ 0. Этот модельный случай соответствует движению ракеты с жидким топливом, определяемому уравнением m x = M u + M i. (6)

Равенство (6) является обобщением уравнения И.В. Мещерского для тела переменного состава, учитывающим относительное движение РТ.

Разделим временной интервал движения РС T = (- ∞ <  t < + ∞) на следующие интервалы: T 1 = (- ∞ <  t ≤ 0), T 2 = (0 ≤ t ≤ τ ) и T 3 = ( т <  t <  + ®), так что Te ( T 1 и T 2 и T ₃).

Из уравнения (6) для t e T 1 следует:

M x = u In---+ l

M 0

M

+

M

t

J

- w

M12 IM )

ds

В режиме движения, при котором имеем M (+ ®) = M 1 , M ( +w ) = 0, из соотношения (7) для t e T получаем величину конечной скорости РС:

+ w 'A2

Mo

Vk = - u lnTT + l I ds, kMM

1      - w \7

где обозначено M ₀ = M (0), M 1 = M ( t ) [23].

Таким образом, в отличие от классических результатов задач ракетодинамики, в данной модели РС при заданном режиме движения скорость системы согласно формулам (7), (8) зависит от места расположения её соплового блока ( l > 0 или l < 0) и закона отде-

⁸ Охоцимский Дмитрий Евгеньевич (1921-2005) – академик АН СССР, профессор МГУ, специалист в области РС и механики космического полёта.

ления массы РТ этой системы. Этот результат качественно отличен от положений и выводов, основанных на формулах Мещерского (4), (5) и Циолковского (3).

Данная неклассическая задача является одним из многочисленных примеров продолжающегося развития основанной Мещерским теории реактивного движения.

Жизнь и научное творчество

И.В. Мещерский прожил творчески активную жизнь, наполненную выдающимися научными достижениями в области механики.

На жизненном пути ему приходилось преодолевать немало трудностей. Родившись в бедной мещанской семье, он в силу сословного положения и материальной необеспеченности семьи с трудом поступил в классическую гимназию, обучение в которой семья не имела возможности оплачивать. Во время обучения в университете, не получая помощи от родных, Иван Всеволодович существовал на средства, которые приносили ему частные уроки и студенческая стипендия. Кроме того, он работал оплачиваемым делопроизводителем в студенческом физико-математическом кружке ( А.Г. Нагибина. Научно-технические ведомости СПбГТУ. 1999, № 1).

Встречались трудности и в последующие периоды его жизни. В конце XIX-го и начале XX-го веков область его научного творчества и исследуемые им проблемы считались малоактуальными и не перспективными, а поставленные им задачи (в частности, задачи реактивного движения) - фантастическими. Этими вопросами занимались одиночки, а исследования в этом направлении носили случайный характер [12].

Более того, даже известные в науке современники И.В. Мещерского считали избранное им научное направление надуманным, далёким от реальности. По этой причине его магистерская диссертация [2] при защите встретила холодный приём и непонимание [21]. Ему приходилось настойчиво преодолевать это предубеждение при помощи обоснованной аргументации и убедительных доводов. Этому способствовал его волевой характер, последовательная настойчивость, глубокое убеждение и вера в актуальность и перспективность своих исследований.

История мировых достижений в области реактивной техники доказала его правоту, гениальную проницательность и силу научного предвидения. "Технический прогресс в об-

ласти реактивного движения … убедительно доказывает … глубину мысли оригинального научного творчества И.В. Мещерского" [13].

"Основная заслуга И.В. Мещерского перед наукой заключается в том, что он первый создал теоретические методы [основы] … решения многообразных задач движения тел, масса которых изменяется …" [21]. Он создал новое научное направление в механике, выработал плодотворные идеи, которые и до настоящего времени являются животворным источником дальнейшего развития теории массоизменяемых механических систем.

Выдающийся учёный, талантливый педагог и деятель высшего образования – таков многогранный облик Ивана Всеволодовича Мещерского, создателя основ теории реактивного движения.