Speed up linear scan in high-dimensions by sorting one-dimensional projections

Similarity search in high-dimensional space has many applications such as multimedia retrieval, time-series matching, exploratory data analysis, and the like. The most typical type of similarity search is the k -Nearest Neighbor ( k -NN) search in such cases. One serious problem in achieving efficient and effective similarity search is the notorious "curse of dimensionality". Efficient indexing structure is crucial for achieving efficient and accurate searches. Some indexing structures have been proposed [1], but these indexing methods degenerate to a linear scan when dimensionality exceeds a certain threshold. Generally, it's very difficult to design an efficient index structure suitable for different dimensionality and adaptive to data distributions.

This work was supported in part by the Fundamental Research Funds for Central Universities Under Grant No.JY1000090300.

Traditional tree-based indexing structures, which include data-partitioning-based and space-partitioningbased structures [1][2], always degenerate to visiting the entire data set when the dimensionality is high. Given this point, for k-NN queries in a high-dimensional space, linear scan remains an efficient search strategy for similarity search [3]. On the other hand, for the diskbased indexing structure, in which it is assumed that the databases are too large to fit into main memory, I/O operations often dominate the cost of query processing because of the relatively low transfer speed between memory and disk. The actual page access strategy has a significant impact on the I/O cost. The linear scan strategy avoids seeking the specified page, and it is much faster than random access strategy.

Besides linear scan, VA-file approach and its variations also apply linear scan strategy to read the compressed file, which suggests accelerating the linear scan by the use of data compression and filtering of the feature vectors [2]. However, all these methods using linear scan strategy usually need to access the whole data file. In this paper, we proposed a simple and efficient index structure based on extended B+-tree, which can facilitate efficient k-NN searches in high-dimensional space. In the extended B+-tree, two kinds of key are embedded in the leaf nodes. One key stores the projection value on the line determined by the first Principal Component, and the other stores the distance between data point and reference point. By performing Principal Component Analysis, the one-dimensional projection values of data points on the first principal component is sorted in the ascending order and indexed using the B+-tree. The distance of each point to the center of dataset is also embedded in the leaf nodes of the B+-tree. During the search, only a small proportion of data file need to be linearly scanned.

We show that this new structure can be used with other existing indexing methods applying linear scan. It has the following advantages over existing high-dimensional indexing structure. (1) The searching process applies linear scan strategy, and only a small part of data file need to be accessed during the search. (2) It can also reduce the dimensionality of distance calculation by using triangular inequality, which can reduce the processor time.

The rest of this paper is organized as follows. In section II, we survey the main current indexing methods. Our new search strategy and the corresponding k -NN search algorithm is introduced in section III. An extensive performance study is reported in section IV, and finally, we conclude our paper.

• II.    R elated work

Some traditional index structures focusing on multidimensional spaces had been proposed for the similarity search. Recent studies show that these index structures for nearest-neighbor search will, as dimensionality increases, always degenerate to a linear scan. To tackle this phenomenon, some approaches had been presented. In this section we discuss these related works in three categories: (1) dimensionality reduction approach; (2) VA-file approach; (3) one-dimensional mapping approach based on distance computation.

A.    Dimension Reduction

To scale to higher dimensionalities, a commonly used approach is dimensionality reduction (DR)[4]. The DR approach first condenses most of information in a dataset to a few dimensions by applying PCA or other techniques. Two strategies for dimensionality reduction were presented [5]. The first one is Global Dimensionality Reduction (GDR), in which all the data as a whole is reduced down to a few dimensions. This strategy is not effective to handle datasets that are not globally correlated. The other strategy, called Local Dimensionality Reduction (LDR), divides the whole dataset into separate clusters on the basis of the correlation of data, and then reduces the dimensionality in each cluster. The GDR technique works well when the data set is globally correlated. In practice, datasets are often not globally correlated. However, there may exist subsets of data that are locally correlated, therefore the LDR significantly outperforms the GDR.

Another LDR method, called MMDR, was presented using the Mahalanobis distance, which can identify the ellipse shaped clusters in the subspace [6]. Mahalanobis distance could be applied to find ellipsoidal correlated data, by taking local elongation into account. The elliptical correlated clusters are more suitable for dimensionality reduction than spherical-shaped clusters. To improve the performance of indexing method which need pre-computing the distance, a general cost model of LDR for range queries was presented [7]. According to the cost model, a new LDR method, called PRANS, has been proposed. One of the goals of the model is to prune more data points using triangle inequality.

B.    VA-file Approach

Traditional index structures for nearest-neighbor search will, as dimensionality increases, always degenerate to visiting the entire data set. Given this point, Vector Approximation file (VA-file) approach applies no index structure but linear scan, which suggests accelerating the linear scan by the use of data compression and filtering of the feature vectors [2].

VA-file approach was not specially designed for real-life datasets. In the recent literature, some extensions of vector approximation approach have been proposed for multimedia retrieval. One kind of extensions was keeping the linear scan, which achieves better query performance by reducing the approximation file size or improving the filtering efficiency. For non-uniform distributed datasets, VA+-file approach was presented [8], which uses Principal Component Analysis to reduce the correlation of data at different dimensions, and the data in each dimension is clustered into a pre-assigned number of grids using Lloyd's algorithm. The drawback of these methods is that they have to sequentially scan the whole approximation file during the query process. PCVA method is the first approach which can reduce the candidates of approximate vector to be linearly scanned [9]. By sorting the one-dimensional projections on the first Principal Component, only a small set of approximate vectors need to be linearly scanned during the search.

For instance when the image data sets are highly skewed and the feature dimensionality is not very high, traditional multi-dimensional indexing techniques remain more effective. Some new index structures combining the VA-file and tree-based indexing structure have been presented which include IQ-tree [10] and GC-tree [11]. These methods can't sequentially scan the approximation file. However they reduce the number of approximation vectors accessed and then reduce the processor cost. They still face the difficulty of dimensionality cures and can't reduce the I/O cost when dimensionality is high.

C.    One-dimensional mapping

One-dimensional indexing approaches provide another direction for high-dimensional indexing using one dimensional mapping. The examples are the Pyramid technique [12] and iDistance [13]. The Pyramid technique divides the d -dimensional data space into twodimensional pyramids and then cuts each pyramid into slices each of which forms a data page. It provides a mapping from d -dimensional space to singledimensional space. The iDistance approach first partitions the space into several clusters, and then transforms a high-dimensional point into a single-dimensional value with reference to its corresponding reference point. B⁺-tree is used to index the transformed values. A query in the original data space is mapped to a region determined by the mapping method, which is the union of onedimensional ranges. Data points are retrieved based on these one-dimensional range queries.

One-dimensional index structures work well in low to medium dimensionality spaces (up to 30-40 dimensions). However, one-dimensional transformation methods are not specially designed for very high-dimensional datasets. When the dimensionality increases, overlap of partitioning spheres can lead to more intersections by the query sphere, and more points having the same similarity value will cause more data points to be examined. Moreover, building the partitioning clusters and selecting the number of clusters can be more difficult with the increasing dimensionality.

• III.    P artial linear scan

In our discussion, we assume that DB is a set of N points in d -dimensional space. We use i e {1,..., N } to range over data points. Hence, p_i denotes an individual data point, and p_{i , j} denotes the j -th component within p_i . A k -NN query finds the k vectors in the database closet in distance to a given query vector q . Throughout this paper, we use the Euclidean distance between q and p_i as our metric, which is defined as follows:

^dist ( q , P i ) = j £ d = 1 ( q ,- P i /)²

To realize the linear scanning of k -NN query, a minimum distance array kDist [] of size k , is employed. kDist [] is sorted in ascending order. Fig. 1 shows the basic linear scan algorithm for k -NN search.

Algorithm kNNSearch ( q , k )

• 1.    Initialize kDist[] with MAXREAL

• 2.    for i =1: N

• 3.    Calculate dist(p i ,q)

• 4.         if dist(p i ,q)

• 5.           kDist[k] = dist(p i ,q)

• 6.         sort kDist[] in ascending order

Figure 1. k-NN basic search algorithm.

In the following, we first describe two kinds of onedimensional mapping method based on projection and distance computation and the corresponding algorithm of partial linear scan. Then, the structure of extended B+-tree is presented.

A.    Partial linear scan using projections

Principal Component Analysis (PCA) is a widely used approach to transform points in the original space into another space. Using PCA, most of information in the original space is condensed into the first few principal components. Suppose we have two d -dimensional points, p_i and q , which can be transformed into P_i and Q in the PCA space. P_{i ,1} is the projection value of P_i on the first principal component, and Q ₁ is the projection value of Q on the first principal component.

When mapping the data points to one-dimensional projections on the axis determined by the first principal component, a simple partial scan algorithm can be designed. Fig. 2 shows the points accessed when performing partial linear scan. Data points between two broken lines need to be accessed if projection values are applied in partial scan algorithm. The similar algorithm has been presented in PCVA [9], which is a bidirectional linear scan algorithm. The data points are sorted in ascending order according to the one dimensional projections. When computing the distance between Q and P_i , the distance between the one-dimensional projections of Q and P_i is calculated firstly. If dist ( Q j , P i , j ) > kDist [ k ] , we do not need compute dist ( Q , P i ) on all the dimensions. Further, the linear scan on this direction can be terminated [9].

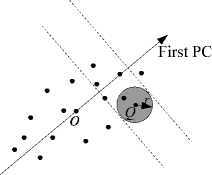
Figure 2. Partial linear scan using projections

B.    Partial linear scan using distances

Suppose O be a reference point, and P_i , Q be two points in the PCA transformed domain. The data points can be mapped to one-dimensional values by computing the distance. The Euclidean distance function dist ( ) has the following properties called triangular inequality:

dist ( P i , Q ) >  dist ( Q , O ) - dist ( P i , O )|

The partial scan algorithm can be designed according to the triangular inequality. Fig. 3 shows the points accessed when performing partial linear scan using distance computation. Data points in the shade region need to be accessed. The one-dimensional mapping values, dist ( P i , O ) , are computed firstly, and the data points are sorted according to the one-dimensional distances. When performing k -NN query, if the difference between dist ( Q , O ) and dist ( P i , O ) is larger than kDist [ k ] , then P_i can be rejected without computing dist ( P i , Q ) .

C.    Combination of projection and distance computation

In previous sections, we have discussed how to design partial scan algorithm using one-dimensional mapping. The key idea of the algorithm is that the one-dimensional values are sorted and the first accessed point needs to be found. We measure how good the partial scan algorithm using filtering effectiveness defined as f = Nf /N , where N_f is the number of data points can be rejected using the projection or distance computation. The larger filtering efficiency means less data points need to be accessed during the query.

In this subsection, we focus on how to combine the two filtering strategies and get the best filtering efficiency. Fig. 4 shows the points accessed when combining two filtering strategies. When combining two filtering strategies, only data points in the shaded region need to be accessed.

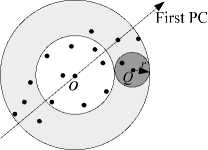
Figure 3. Partial linear scan using distance computation

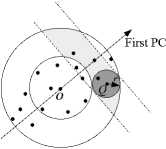
Figure 4. Combination of two one-dimensional mapping

There are two methods to index distances and projections. The first one is sorting data points according to the distances. When performing k -NN search, if data points can not be rejected using triangular inequality, the projections is used to prune data points. The other method is sorting projections. Distances are embedded to further reject data points. The experiment results show that these two methods get almost the same filtering efficiency. The chose of reference point has some effect on the filtering efficiency of distance computation. When combining two filtering strategies, the chose of reference point also affect the query performance. In the experiments, we will have a detailed discussion on how to get higher filtering efficiency by chose an optimal reference point.

D.    Structure of extended B+-tree

An extended B⁺-tree is used to index the two kinds of one-dimensional value. Figure 5 shows the structure of extended B⁺-tree. The projection values on the first PC are sorted and indexed as the key in the B⁺-tree. In the leaf nodes of extended B⁺-tree, the distance of each point to the reference point, D_i , is also embedded. Therefore, each point has two elements in the leaf nodes of extended B⁺-tree. Compared with regular B⁺-tree, the extended B⁺-tree doubles the number of leaf nodes, and the height of the extended B⁺-tree is larger than that of B⁺-tree. The extended B+-tree can be used with other existing indexing methods such as sequential scan, VA-file approach and its variations.

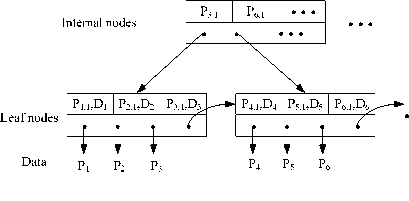
Figure 5. Structure of the extended B+-tree

E.    K-NN search in the extended B+-tree

For the real-life datasets, such as image feature or video feature databases, data are non-uniform distributed, and also correlated. We can map the high-dimensional points to a one-dimensional line using PCA. Just as we mentioned in III.A, we still assume that the two d -dimensional points, pi and q , which can be transformed into Pi and Q in the PCA space. Pi,1 is the projection value of Pi on the first principal component, and Q1 is the projection value of Q on the first principal component. The extended B+-tree is used to index the one-dimensional projections on the first PC. And to reduce the data points accessed, distances to the reference points dist (Pi, O) are also embedded on the leaf nodes.

During the k-NN Search, the Partial Distortion Search (PDS) algorithm is adopted, which is widely used in the vector quantization encoding process. We will introduce it at first. Define dist = ’Y"’ (P ., Q 11 <  m <  d . The ^m          j = 1 i , j , ^J ,

PDS algorithm starts from m = 2 , for each value of m , m = 2, k , d , we first evaluate dist m ( P i , Q ) , If dist m ( P i , Q ) >  kDist [ k ] ,we don’t need to compute dist ( P_i , Q ) on all the dimensions because. dist ( P i , Q ) > dist m ( P i , Q ) >  kDist [ k ] , then P i can be rejected. Otherwise, we go to the next value of m and repeat the same process. The process continues until P_i is rejected or m reaches d . If m = d , then we compare dist ( P_i , Q ) with kDist [ k ], kDist [ k ] will be replaced by dist ( P _i , Q ) and the array kDist [.] should be resorted when dist ( p , Q ) <  kDist [ k ] happens. Figure 6 shows the PDS algorithm.

Algorithm PDSearch ( P i ,kDist[],Q )

• 1.       For m =2 to d -1

• 2.          calculate dist m (P i ,Q)

• 3.          if dist m (P i ,Q)>kDist[k]

• 4.          End of PDSearch

• 5.          calculate dist(P i ,Q)

• 6.            if dist(P i ,Q)

• 7.               kDist[k] = dist(P i ,Q)

• 8.             Sort the kDist[] in ascending order

• Figure 6.    Algorithm of Partial Distortion Search

If the dimensionality is very high, the cost of comparing dist_m ( P_i , Q ) with kDist [ k ] is also high. Since most of the energy is condensed to the first several dimensions, we can perform PDS algorithm only on the first several PCs, if the vector can not be rejected on these dimensions, we directly calculate dist ( P_i , Q ) in all dimensions.

Algorithm kNNSearch (k, q ,O)

• 1.    Initialize kDist[] with MAXREAL

• 2.    Calculate corresponding Q according to q

• 3.    s = LocateFirstAccessVector ( b⁺tree , Q )

  //find the first accessed page according to b⁺tree

  // s is the index of first accessed vector

• 4.    for i= s to 1 //search backward

• 5.          calculate dist 1 (P i ,Q)

• 6.         if dist 1 (P i ,Q)> kDist[k]

• 7.           break //end the search backward

• 8.          else

• 9.              if |dist , (P , ,O)-dist(Q,O)| <  kDist[k]

• 10.               PDSearch ( P i , kDist[] ,Q )

• 11.    for i=s to N //search forward

• 12.         calculate dist 1 (P i ,Q)

• 13.        if dist 1 (P i ,Q)> kDist[k]

• 14.           break //end the search forward

• 15.         else

• 16.            if |dist i (P i ,O)-dist(Q,O)| <  kDist[k]

• 17.                PDSearch ( P i , kDist[] ,Q )

• Figure 7.    Algorithm of k-NN Search

• IV. P erformance S tudy A nd E xperiments

In this section, we performed extensive experiments on the high-dimensional datasets to demonstrate the practical effectiveness of the extended B⁺-tree. First we study the performance of our approach when selecting different reference point. We find that the optimal query performance can be got when the reference point is the origin in the PCA space. The state of the art for retrieving the exact k nearest neighbors in high-dimensional space is the iDistance. The iDistance is also compared with our approach. Experiments results show the superiority of our approach.

Our experiments have been executed under the Windows XP Professional with Intel PIV1.8GHz Processor and 1GB of main memory. The data page size used in the experiments is 4096 Bytes. Each result we show was obtained as the average over 100 k -NN queries, and 10-NN, 20-NN,50-NN query have been performed. In the experiments, we use real-life dataset to evaluate the effectiveness of our method. Two data sets which are widely used in high-dimensional indexing were chosen. The first data set is called COLHIST [14], which contains 68,040 32-dimensional color vectors and was downloaded from The other data set is called LANDSAT[15], which contains 275,245 60dimensional feature vectors extracted from satellite images and was downloaded from

A.    Selection of the optimal reference point

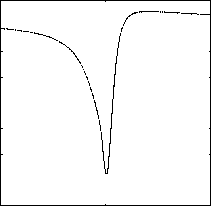
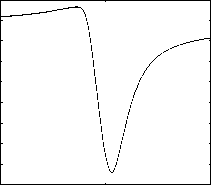
For the partial linear scan, data points can be filtered in the transformed one-dimensional space during the k -NN queries. The one-dimensional value can be got using distance computation. For the same dataset without any partitions, the variance of distances of points can weight the filtering efficiency of partial linear scan. That means larger variance can prune more data points using onedimensional distances during the k -NN search. This observation is also been discussed in our former work [9]. For distance computations, difference points results in different variances. An optimal reference point is a point maximizing the variance of the distances of points in transformed one dimensional space. The optimal reference points lie on the line identified by the first PC [16]. We use CLOHIST to test the variances of distances of points. Fig. 8 and Fig. 9 shows the variances of distance on 32-dimensional and 60-dimensional vectors respectively, when using different coordinate along the first PC as the reference point. From the figure, it can be seen that we can get the largest variance when the reference point lies out of one side of data segment along the first PC.

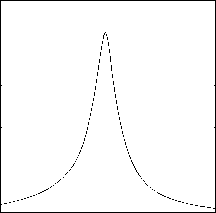
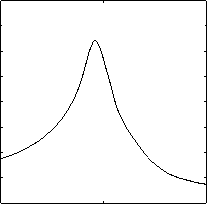
When combining two one-dimensional filtering strategies based on projection and distance, the optimal reference point is the point which can get the largest filtering efficiency. We have selected different coordinate along the first PC and performed 10-NN queries. Fig. 10 shows the filtering efficiency when using difference coordinate along the first PC as reference point. Similarly, Fig. 11 shows the situation on 60dimensional texture features. From the figure, we can see that the largest filtering efficiency can be got when the reference point lies on the center. In the PCA space, the center of dataset 0.18 0.175 0.17 0.165 0.16 0.155 0.15 0.145

is also the origin.

COLHIST

-5                                 0                                 5

Coordinate on the first principal component axe

Figure 9. Virances of distances using different reference points(LANDSAT)

Figure 8.Virances of distances using different reference points (COLHIST)

LANDSAT

Coordinate in the first principal component axe

0.84

0.7

Coordinate on the first principal component axe

Figure 10 .Filtering effectiveness using different reference points (COLHIST)

LANDSAT

0.83

0.82

0.81

? 0.8

0.79

0.78

0.77

Coordinate in the first principal component axe

in the iDistance. However, the performance of eBLS and eBVA are always better than VA-file approach and sequential scan, since only part of data file need to be linearly scanned and it also reduce the dimensionality of distance calculations. Assuming linear I/O cost is 10 times faster than random I/O [5]. The result of I/O cost is shown in Fig. 14 and Fig. 15. The eBLS and eBVA apply linear scan strategy, so they have fewer I/O time than iDistance and eBVA performs the best. It has a speedup factor of about 10 times over iDistance in I/O time. From the results, we can see that the eBLS and eBVA have fewer I/O cost, and iDistance can save the CPU time in the 32-dimensional space. Among the three methods, the eBVA have significantly fewer I/O cost, hence it has the least total response time.

0.95

0.9

0.8

0.75

0.7

0.65

0.85

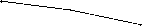
I —I— iDistance

I d eBLS I eBVA

10NN

20NN

50NN

Figure 11. Filtering effectiveness using different reference points (LANDSAT)

B.    Performance study with other indexing structures

In this section, we compare the extended B+-tree with PCVA and iDistance [13]. The extended B+-tree can be used with linear scan and VA-file approach. We call the extended B+-tree used in linear scan as eBLS, and the extended B+-tree used in VA-file as eBVA.

PCVA, eBLS, and eBVA, are linear scan based techniques. The PCVA only uses projections to filter data points. However, in eBVA, the projections and distances are used together to filter data points. Then, the eBVA outperforms PCVA when computing distance in high dimensions.

For k -NN queries in the iDistance, data points are retrieved based on one-dimensional range queries on different partitions. The iDistance also use triangular inequality to filter data points. However, in eBLS and eBVA, both distance and projection can be used to prune data points. We first investigate the filtering efficiency of three methods. Fig. 12 and Fig. 13 compare the filtering efficiency of eBLS, eBVA and iDistance.

For both 32-dimensioanl i and 60-dimensional features, the filtering efficiency of iDistance is larger than that of eBLS and eBVA. It means the iDistance can prune more points using partition technique. The main reason is that in 32-dimensional and 60-dimensioanl space, the nearest neighbor distance is not large and the partition technique is still effective. Although no partition technique is used in eBLS and eBVA, more than 70% data points can be rejected for 10-NN search without high-dimensional distance computation.

The performance of iDistance will be worse than linear scan with increase of dimensionality if I/O time is considered, since the random access strategy is employed

Figure 12. Comparison study of filtering efficiency (COLHIST)

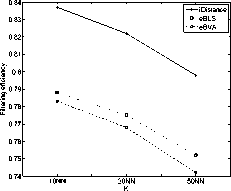
Figure 13. Comparison study of filtering effectiveness (LANDSAT)

I t— iDistance

I. □ eBLS I | • о • eBVA

• ⁰ 10NN             20NN             50NN

  Figure 14. Comparison study of I/O cost (COLHIST)

  
  
  

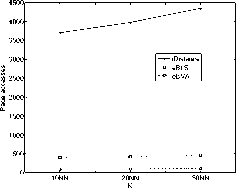
  Figure 15. Comparison study of I/O cost (LANDSAT)

  
  

• V.    R elated W orks

  Traditional multi-dimensional index structures for k -NN search will, as dimensionality increases, always degenerate to visiting the entire data set. Given this point, Vector Approximate file approach applies no index structure but linear scan, which suggests accelerating the linear scan by the use of data compression. VA-file approach was also awarded as the 10 years best paper in VLDB2008. Another index structure applies linear scan is the Omni-sequential. It uses triangular inequality to filtering data points by computing multiple distances to some reference points. However, both VA-file and Omni-sequential need to read the whole data file when performing the k -NN.

To reduce the data points accessed during the query, PCVA method was presented by sorting the projections on the first PC. PCVA applies linear scan strategy, so its query performance is better than linear scan and VA-file approach. The projections on the first PC can be seen as one-dimensional mapping. Another one-dimensional mapping method is distance computation. In the iDistance, distance computation is used to transform a highdimensional point into a single-dimensional value. B+-tree is used to index the transformed values. However, the iDistance is not specially designed for very highdimensional datasets. The performance of iDistance will be worse than linear scan with increase of dimensionality.

• VI.    C onclusion

In this paper, we presented a simple, yet efficient indexing structure, extended B⁺-tree, which can implemented on the linear scan based methods to speed up the k -NN search. In the extended B⁺-tree, two kinds of keys are stored in leaf nodes. One is the projection on the first PC, and the other is the distance to the center of dataset. The projections of data points are sorted and indexed by the extended B⁺-tree. Our extensive performance study demonstrated that our new method (1) reduced the number of data points need to be accessed during the linear scan and (2) outperformed the other indexing structure when the dimensionality is high.