Спекание в напыленной пленке и ОДА-модель процесса

В прозрачной пленке метана с хлором, полученной из газовой фазы на холодной подложке и пересыщенной вакансиями, благодаря светорассеянию на порах визуально наблюдались различные состояния процесса спекания. Установлено ускоряющее действие ультразвука и возможность колебательного режима спекания. Предлагается алгоритм ОДА-модели для процесса.

При распаде метастабильных растворов в течение индукционного периода происходит флуктуационное образование зародышей новой фазы. На следующей стадии, когда пересыщение уменьшается, мелкие докритические зародыши растворяются, а крупные растут (оствальдово созревание).

Явление спекания – тот частный случай, когда роль атомов (молекул) растворенного вещества играют вакансии – пустые места. А роль зерен – поры, получающиеся за счет коагуляции вакансий в конденсированной среде, пересыщенной вакансиями. В напыленной пленке вдали от границы на стадии созревания происходят два конкурирующих процесса – рост закритических пор, которые являются стоками для вакансий, и растворение докритических, которые выступают истоками вакансий. Вблизи границы идет только один процесс: растворение пор и вытеснение вакансий макроскопическим диффузионным потоком к свободной поверхности, отделяющей полупространство новой фазы, которое следует рассматривать, как пору бесконечного радиуса. Кинетика диффузионного процесса образования зерен новой фазы в пересыщенном твердом растворе для неограниченной среды и для полупространства на поздней стадии этого процесса описана аналитически в [1].

Принимая основные положения, обратимся к вариациям в частностях и прежде всего для условий большого пересыщения вакансиями, которое экспериментально достижимо в отдельных случаях при формировании слоя конденсата из газовой фазы на холодной подложке. Скорость изменения радиуса поры R :

dR D    α

=Т(А- Т)’ dt  R    R где

где

D – коэффициент диффузии;

А - пересыщение вакансиями ( А = С - С J;

а = — • V • С„ kT " ,

σ – коэффициент межфазового поверхностного натяжения;

• V – объем одной вакансии ( r ₀ – радиус вакансии);

С _х - концентрация насыщенного раствора. dR                α

Из условия — = 0 получим R-кр = а .

При T = const, полагая ст и Сю неизменными, проследим эволюции на оси размеров пор. При большом А исходное значение Rкр мало, большинство пор - стоки, они растут, снижая А. Причи- на - рост пор, следствие - снижение А и увеличение R . Критический радиус догоняет все боль-dR кр шее количество пор, меняя знак производной для них с плюса на минус. Стоки пор превращаются в истоки. Пересыщение приближается к минимуму, а возрастающее значение Rкр – к верхней точке поворота на оси размеров пор. После поворота критический радиус снижается, изме-dR нив знак производной — почти всем порам. Все поры - истоки, пересыщение А возрастает, а Rкр уменьшается, оставаясь догоняющим (он есть следствие). В слое конденсата (пленке), в той части, которая близка к свободной поверхности, образно выражаясь, действует стационарный «насос» для вакансий, неизменно снижающий А в системе. При недостаточной плотности макроскопического диффузионного потока на удалении от границы величина А снижается несущественно и остается столь значительной, что Rкр – мал и обгоняет положение максимума в мгновенном распределении пор по R, двигаясь в направлении отметки r0 – размера отдельной вакансии. Для конкретной системы становится принципиальным – будет ли достигнута нижняя точка поворота.

Если это происходит, то следует говорить о колебательном режиме спекания. Колеблются R ,   ,

• А , R . Для соответствующей пары переменных может быть получена фазовая диаграмма, на- кр            dR

пример для R и .

Экспериментально наблюдался колебательный режим спекания в пленке, полученной намораживанием конденсата из молекулярных потоков на холодной подложке, охлажденной парами жидкого гелия. Образец приготавливался, как реакционная смесь для исследования низкотемпературных кинетик фотохлорирования метана в твердой фазе [2, 3]. Сопутствующие явления спекания и отчасти распада твердого раствора хлора в метане предстали наглядно в прозрачном образце благодаря светорассеянию прежде всего на порах и отчасти на кристаллах хлора.

Степень спекания в образце определяющим образом влияла на результаты лазерного фотолиза хлора в матрице метана [2]. Предыстория фотолизуемого участка образца, а именно, стадия спекания, устанавливала квантовый выход расхода хлора.

Обращаясь к условиям приготовления образца, остановимся на отдельном опыте, при котором температура подложки выбиралась из условия T ₀  0,3 Тпл для двух компонентов смеси,

Т ₀ = 28 К удовлетворяла этому условию. При напылении (~30 мин) и после прекращения подачи газов температура поддерживалась с точностью лучше ±0,5 К. На рисунке 1 показан медный хладопровод, обжимающий через индиевые прокладки круглую подложку (кварц, флюорит, медь) с диаметром площадки для конденсата 40 мм. Сопла для двух газов – трубки диаметром 3 мм, ориентированные на центр площадки под углом 10 ^ 15° к оси. Сопла не имели насадок. Вакуум в криостате – 10^–7. Очищенные газы молекулярными пучками направлялись к холодной подложке, первым подавался матричный газ – метан, с увеличивающимся расходом в течение 1 минуты до установившегося значения 10^{18 молекул} , затем хлор с меньшим расходом в пропорции 1 : 4. Установленные расходы газов поддерживались до конца напыления. Итогом напыления в течение 30 минут была прозрачная пленка, по легкой желтизне которой визуально можно было судить о некоторой радиальной неравномерности распределения хлора – в центре площадки его было больше. Более точные представления дают графики на вставке А (рис. 1) соответственно для толщины: d , мкм ( r ) в диапазоне 90 ^ 60 мкм; для оптической плотности D 1 , в полосе диссоциативного поглощения молекулярного хлора на X = 325 нм (He-Cd лазер), диапазон для D 1 от 6 в центре до 3 на периферии; а также для радиального распределения температуры: T , K ( r ) в диапазоне 33 ^ 28 К.

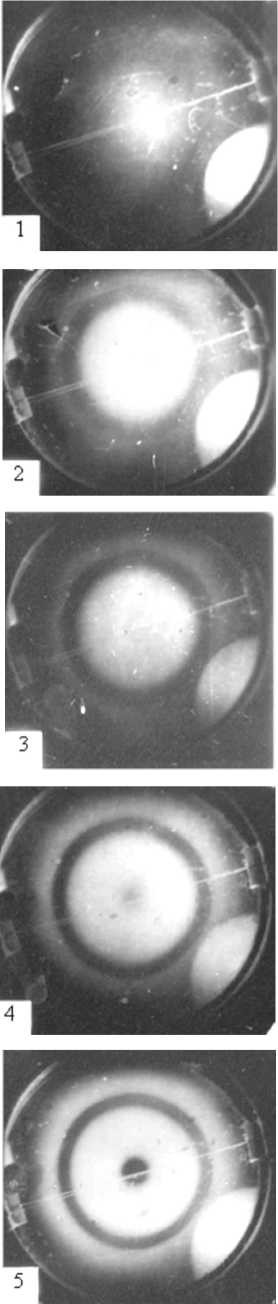
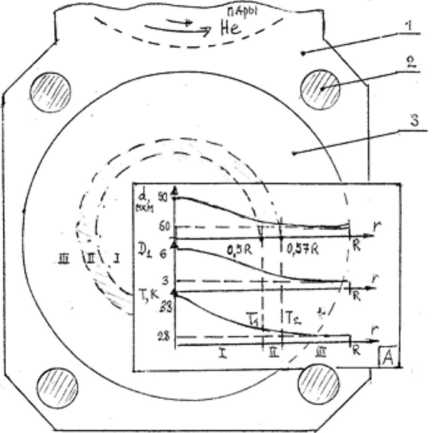
Рис. 1. Медный хладопровод, обжимающий через индиевые прокладки круглую подложку (кварц, флюорит, медь) с диаметром площадки для конденсата 40 мм:

1 – медный хладопровод; 2 – четыре пьезоэлемента; 3 – подложка и напыленная пленка с выделяющими кольцевые зоны I, II, III изотермами T ₁ и T ₂; вставка A: A1 – радиальное распределение толщины пленки d , мкм ( r ); А2 - распределение оптической плотности D 1 на X = 325 нм, указывающее на неравномерность радиального распределения хлора в матрице метана;

А3 – радиальное распределение температуры на подложке Т , К ( r )

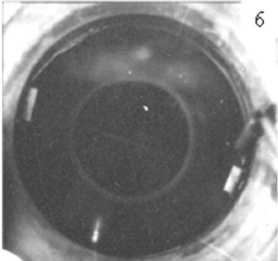
Рис. 2. Видеоряд состояний кольцевых зон на пленке (в отраженном свете), отличающихся стадиями процесса спекания за первые 30 мин после окончания напыления. Начало отсчета времени: после прекращения подачи газов:

0 – абсолютно прозрачная пленка (в видеоряд не включена); от 1 до 5 соответственно 1, 3, 5, 7, 10 минут; 6 – повторное помутнение кольцевой зоны II на 30-й минуте (снимок сделан на просвет; пятно в нижней части – фотолизующий лазерный пучок)

Пользуясь преимуществами прозрачного образца, применим термины «замутнение – просветление», описывающие эволюции кольцевых зон на образце. Видеоряд кольцевых зон, полученный в отраженном свете, представлен на рисунке 2, позиции 1–5; он завершается позицией 6, полученной на просвет к 30-й минуте наблюдения. Видеоряд получен для пленки на кварцевой подложке, замена материала подложки на флюорит и медь не внесла принципиальных изменений. Это можно объяснить высокой степенью неупорядоченности в конденсате – его неравновесным стеклообразным состоянием, формирование которого может быть детализировано.

В опыте при потоках газов средней интенсивности соблюдались условия быстрого переохлаждения до Т ₀ 'ST 0,3 Т _пл, в таких условиях частично адсорбируются как отдельные молекулы – самый маленький зародыш, так и кластеры, которые возникают в молекулярном пучке. В молекулярных пучках, истекающих из сопел в вакуум, молекулы, сталкиваясь друг с другом, объединяются в димеры, тримеры и т. д., которые в свою очередь могут распадаться. Образовавшиеся в молекулярных пучках кластеры имеют как кристаллографическую, так и некристаллографическую упаковки. Учитывая конкретную особенность – полиморфизм твердого метана [4], следует ожидать заметного разнообразия для кластеров этого газа, достигших подложки. Молекулярные пучки перекрываются вблизи подложки, и неизбежно возникают кластеры из двух сортов молекул.

Детализация молекулярно-кластерной динамики в адсорбционном слое предполагает, что отдельные молекулы и кластеры при соударении с подложкой образуют двумерный газ, они совершают тепловые колебания вдоль поверхности и по нормали к ней [5]. В результате они могут перескакивать в соседние положения адсорбции молекулярно-шероховатой поверхности или покидать ее. Блуждая по этой поверхности, молекулы и кластеры находят состояния, в которых присоединяются сразу двумя или тремя связями. Адсорбционный слой обменивается частицами как с твердым конденсатом, так и с газом; в нем создаются зародыши кристаллов.

В данном конкретном случае: зародыши кристаллов метана всех известных четырех форм и некристаллических упаковок, зародыши кристаллов хлора и зародыши «кристаллов пустоты». При столь быстром охлаждении именно этим нанонеоднородностям – кристаллам пустоты суждено становиться микронеоднородностями, заполненными насыщенным паром – порами, по рассмотренной выше схеме в процессе спекания, который может протекать в колебательном режиме.

Целью работы является рассмотрение феноменологии спекания метастабильного твердого раствора в виде прозрачной пленки, полученной из газовой фазы в условиях быстрого переохлаждения на холодной подложке, по видеоряду, зарегистрированному благодаря светорассеянию на порах, с рассмотрением ускоряющего воздействия ультразвука, отчетливо выявляющего три и более полных колебания спекания, а также предложение алгоритма ОДА-модели для машинного моделирования колебаний спекания.

Из представленного на рисунке 2 видеоряда следует, что на образце выделяется кольцевая зона примерно на середине радиуса. Далее будем говорить о зонах I, II, III, которые разделяются изотермами Т ₁ и Т ₂, показанными на рисунке 1. Какие конкретные локальные условия роста пленки в той части образца, которая соответствует средней кольцевой зоне II, способствовали ее выделению – осталось невыясненным до конца, но поведение этой части характеризуется небольшим помутнением на № 1 (1 мин), ослаблением помутнения на № 2

(3 мин) и полной восстановленной прозрачностью на № 4 (7 мин), легким повторным помутнением на № 5 (10 мин), медленно возрастающим к 30-й минуте наблюдения – № 6. Этот снимок сделан с обратной стороны подложки. Соучастие в спекании пленки еще и распада пересыщенного твердого раствора хлора в метане в центральной зоне I может снижать достоверность достижения повторного помутнения во II зоне тем, что сюда выносятся кристаллики хлора из зоны I. Особенность поведения самой теплой зоны I, а именно ее запаздывание по просветлению, возможно, связана с тем же хлором. К 30-й минуте (№ 6) зона I просветляется полностью, и повторное ее помутнение очень затянуто по времени, но за «время жизни» образца в эксперименте – примерно 4 часа, второе колебание завершалось просветлением и начиналось третье помутнение. К этому времени в холодной зоне III только начиналось второе помутнение.

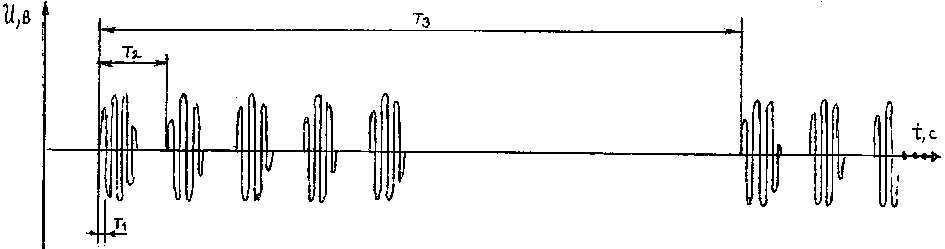
Рис. 3. Форма сигнала для возбуждения пьезоэлементов.

I adeT au пёааТ aa ey: Т 1 = 2 ■ 10^-3 с, Т ₂ = 3 ■ 10^-2 с и Т ₃ = 3 ■ 10^-1 с

Опытным путем установлено ускоряющее действие ультразвука. На рисунке 1 (позиция 2) показаны четыре пьезоэлемента из пьезокерамики ЦТС, установленные на хладоп-роводе, возбуждение которых осуществлялось сигналом, представляющим собой серии радиоимпульсов, показанные на рисунке 3. Период заполнения Т ₁ = 2 ⋅ 10^–3 с, периоды следования радиоимпульсов Т ₁ = 3 ⋅ 10^–2 с и Т ₂ = 3 ⋅ 10^–1 с. Форма сигнала, подобранная с учетом возможных резонансных эффектов в пористой структуре спекающейся пленки, обогащена компонентами в низкочастотной части спектра. Именно при такой форме сигнала происходила ускоренная эволюция указанных трех кольцевых зон. За 15 минут наблюдения в зоне II проходили три полных колебания спекания, сдвинутое по фазе затухающее колебание в зоне I было в состоянии третьего помутнения, а холодная периферическая зона III отставала на одно полное колебание.

Объяснение ускоряющего действия ультразвука следует связывать с увеличением коэффициента диффузии D. Полагая σ и V маломеняющимися величинами, отметим некоторое возрастание средней энергии теплового движения и, следовательно – Т, К, что изменя-dR ет величину α, но не столь заметно, по сравнению с увеличением D. Увеличивается , то dt есть скорость движения по оси размеров пор. Важным является и то, что ускорившийся вынос вакансий макроскопическим диффузионным потоком через свободную поверхность еще не успевает снизить пересыщение ∆, амплитуда колебаний которого остается большой. Так же амплитуда колебаний Rкр остается достаточной для возникновения нижней точки поворота.

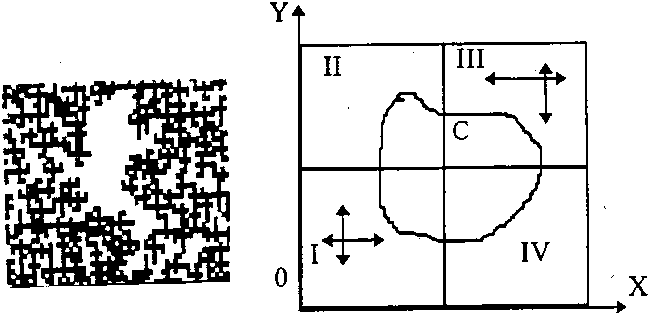
Рис. 4. Кластер вакансий и схема для матрицы вероятностей в окрестности растущего кластера (стока вакансий) в ОДА-модели для колебаний спекания

Для компьютерного моделирования процесса за основу взята ОДА-модель [6]. Используя гипотезу универсальности [7], примем базовым элементом точку – одноузельный элемент, не различая молекулы метана и молекулы хлора. Распад пересыщенного вакансиями твердого раствора можно моделировать, используя модифицированную версию ОДА-модели. Для этого требуется алгоритм организации микроскопических диффузионных потоков к зерну новой фазы или от него и управление их переключением. Зерна новой фазы – это агрегаты вакансий или кластеры вакансий. Примерный кластер вакансий представлен на рисунке 4. Сформируем окрестность кластера в виде квадрата со стороной, равной удвоенному размеру кластера, с центром, совпадающим с центром масс кластера, как показано на рисунке 4 справа. Если это растущий кластер – сток вакансий, то алгоритм предполагает «снос» к центру С, который обеспечивается увеличением вдвое вероятностей перескока в соответствующих направлениях. Так, для квадранта I – в направлениях + X , + Y ; а для квадранта III – в направлениях – X , – Y . Если это распадающийся кластер – исток вакансий, то матрицу вероятностей для I квадранта надо приписать III, и наоборот, тогда организуется диффузионный поток от центра кластера С. Аналогично для квадрантов II и IV. Переключением стоков на истоки и наоборот управляет подсчитываемая периодически величина R _кр, для определения которой требуется знание пересыщения – ∆ . При определении пересыщения величина С _∞ может быть принята параметром модели. В модели предполагается осуществить инверсию пустых узлов в занятые. После инверсии блуждать и агрегировать будут вакансии, а ранее занятые узлы становятся пустыми.

На рисунке 5 показаны три области спекающейся пленки, отсчет которых ведется от свободной поверхности. Особенность области O– Y 1 состоит в том, что над ней находится кластер вакансий бесконечно большого радиуса, то есть постоянно закритический и растущий всегда. В этой области алгоритм предписывает невозможность слипания вакансий, и в матрице вероятностей для этой области задается снос к границе, то есть организуется макроскопический диффузионный поток. В области Y 1– Y 2 происходит растворение пор, то есть присутствуют только распадающиеся кластеры – истоки. В самой удаленной области Y 2– Y 3 развиваются два конкурирующих процесса и практически не снижается пересыщение ∆ , оно при оптимальном подборе параметров модели должно совершать колебания, как и величина R _кр. Начальные значения Y 1 и Y 2 – параметры модели. Далее они увеличиваются, сжимая нижнюю область вплоть до полного ее исчезновения, что означает прекращение колебаний спекания и переход в асимптотический режим.

Свободная поверхность

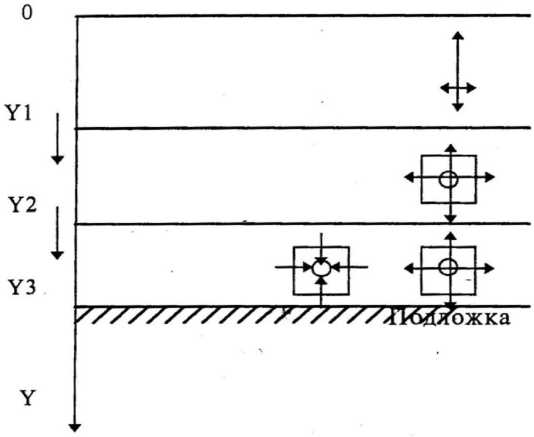
Рис. 5. Три области в пленке при спекании с истоками и стоками вакансий. Ось Y направлена от свободной поверхности в глубину пленки к подложке

В неравновесной системе с высоким уровнем пересыщения вакансиями, имеющей свободную поверхность, спекание может протекать в режиме затухающих колебаний. При моделировании колебаний спекания может быть применен предложенный способ создания переключаемых стоков – истоков вакансий и макроскопического диффузионного потока к свободной поверхности.