Спектр частот, распределение поля и потери мод в трёхзеркальном кольцевом оптическом резонаторе

Развитие науки и техники за последнее десятилетие привело к значительным достижениям в области навигационных систем. Лазерные гироскопы, используемые в таких системах, обеспечивают высокую точность измерений угловых скоростей. Сейчас такие устройства используются в авиации, морской навигации, гирокомпасах и др. Для расширения области их применения необходимо рассматривать уже сверхбольшие и сверхмалые размеры гироскопов, которые смогут использоваться в научных исследованиях, беспилотных аппаратах.

Оптимальными для них являются трёхзеркальные резонаторы. Подобная конфигурация резонатора имеет минимально возможное количество зеркал и поляризацию высокого качества, поэтому приборы на её основе мало чувствительны к магнитному полю.

Несмотря на широкое распространение лазерных гироскопов с треугольными резонаторами, опубликованные данные о расчёте и экспериментальном исследовании модовых параметров таких систем остаются недостаточно полными для их эффективного практического использования. В частности, отсутствуют экспериментально подтверждённые

• (с) Цеваков В. А., Савельев И. И., Сухов Е.В., Брапдукова В. В., 2025

2.    Исследуемый резонатор

@ Федеральное государственное автономное образовательное учреждение высшего образования «Московский физико-технический институт (национальный исследовательский университет)», 2025

сведения о частотном спектре, дифракционных потерях резонатора, а также о нюансах его юстировки. В связи с этим задача комплексного теоретического и экспериментального изучения модовых характеристик треугольного резонатора, поставленная в настоящем исследовании, приобретает особую актуальность. Хотя выражения для частотных спектров и модового анализа приведены в работе [1], в ней не учитывается влияние фазовой анизотропии зеркал резонатора. Кроме того, в доступной литературе полностью отсутствует анализ дифракционных потерь мод в резонаторах треугольной конфигурации.

В работе рассматривается резонатор лазерного гироскопа с равнобедренным треугольным контуром, состоящим из одного сферического и двух плоских зеркал, установленных в вершинах при основании (рис. 1).

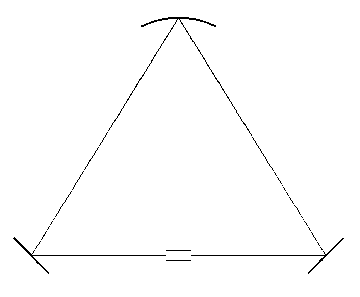
Рис. 1. Оптическая схема резонатора

В центре основания расположена диафрагма. Параметры резонатора представлены в табл. 1.

Таблица!

Параметры резонатора

Периметр	345 мм
Радиус кривизны зеркала	5 м
Угол падения на сферическое зеркало	25∘
Диаметр диафрагмы	2,1 мм

3.    Теоретический анализ спектра частот

В работе [1] для расчета представлено следующее выражение:

V mnqp = AVg (q + 2£) + AV m (т + |^ + AV n ^™ + ^^ ,

где Avg — разность частот между продольными модами, Avm =

Av n = 217 arccos (1 - 'щ^)

2^ arccos (1 - -^)

И

— разность частот между поперечными модами и основной

модой без учёта фазовой анизотропии зеркал (где R — радиус кривизны сферического

'зеркала. L — периметр. ^ — угол падения на сферическое 'зеркало), q — порядок спек

тра, т определяет число нулей поля в плоскости резонатора, а п — в перпендикулярной плоскости. £ равно 1 при т нечетном н 0 при т чётном.

Данное выражение было выведено без учета поляризации излучения в резонаторе (из- за нечетного количества зеркал р- и s-поляризации сдвинуты относительно друг друга на половину межмодового частотного интервала) и анизотропии зеркал (дополнительная разность фаз между р- и s-компонентами излучения, возникающая при отражении от зеркал), которая в нашем случае присутствует [5]. Поэтому были введены дополнительные члены Avp и Ava [4]:

^v mnqp

= A i)q (q + 2 £ ) + Av m (m + |)

+ Av n

(n+D

+ AV p P + Av_ap,

где Av_p — разность частот между основными модами с разной поляризацией, р — число, равное 1 для моды с р-поляризацией и 0 для моды s-поляризации, Av_a — сдвиг частоты, обусловленный фазовой анизотропией зеркал (найден как разность расчетного и экспериментального значений расположения мод для р-поляризации).

4.    Теоретический анализ дифракционных потерь мод

Дифракционные потери мод были оценены двумя методами: первый опирался на известные зависимости потерь от параметра устойчивости д и числа Френеля [2], а второй базировался на предположении, что потери резонатора эквивалентны потерям лазерного пучка с идентичным распределением поля вне резонатора при прохождении через диафрагму аналогичных размеров. В рамках второго подхода определялась доля мощности пучка, не прошедшая через диафрагму.

Оценка дифракционных потерь основной и двух первых поперечных мод по числу Френеля производилась по приведенным зависимостям в работе [2]. Пучок в кольцевом резонаторе астигматичен (эллипс в сечении у основной моды), а данные в [2] приведены для стигматичного пучка (круг в сечении у основной моды). Поэтому потери определялись для стигматичных пучков с радиусами поперечных сечений, равными полуосям реального сечения пучка. И для оценки дифракционных потерь основной моды было взято среднее арифметическое, а для оценки потерь поперечных мод бралась полусумма полученных в нашем предположении потерь поперечных мод с радиусом сечения, равным одной полуоси реального сечения пучка, и основной моды с радиусом сечения, равным другой полуоси. Число Френеля для данного резонатора оказалось равным N = ^ = 5, 05, г де a — радиус диафрагмы, д = 0, 92 для оси Хид = 0, 94 для оси Y. Потери оказались равными:

AFoo = 0,14%; AFW = 0, 32%; AF01 = 0, 51%.

Для оценки дифракционных потерь основной и первых поперечных мод резонатора вторым способом используем предположение, что реальные потери равны:

Я    ^u m n ^(x,y^)dxdy

Х 2+ у 2 ^ Г 2

^Fmn = ¹    +^

Я ^u mn (x,y)dxdy

-∞ где Umn(x,y) — распределение поля в идеальном резонаторе без диафрагмы. Как известно, поперечное распределение поля в идеальном резонаторе описывается функцией Гаусса:

U mn^ y) = U₀H mn (x,y)e

(^+£),

где Uo — максимальное значение поля, a и b — ширина. пу^тпса. на. уровне 1/e от максимального значения поля вдоль осей x и у соответственно, H_mn(x,y) — полиномы Эрмита.

Таким образом, для оценки потерь основной и первых поперечных мод необходимо найти интегралы:

U2e

(    ^2 )

а ^{2 +} Ь ²

dxdy,

х‘ 2+ у ² ^ г^

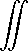
-2 ( ^р +«2 )

2.2,  2 «2 + 1²

U 0 X e 4       '

dxdy,

x' 2+ y'² Д г^

+  )

U2y²e <«2 ¹² ) dxdy.

х ²+ у ² Д Г 2

Вычисления проводились численно и аналитически, с переходом в эллиптическую систему координат и с использованием приближенней с учетом малости аргумента | ^a 2^ | к 0,1. Были получены следующие выражения:

P00

e

2r.d ~22

+ e

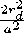
_2Д    _2Д   а2 - b2 P10 = e «2 + e 12 + а2 + b2	4r2         2    2-2       2    2^2             2 2?           4 r d d      /лd 1лd          a b               d e «2+12 + e «2 + 4e i2 — 2^—.----^r2e «2+ 1 2 ,   (10> a2            b2              (a2 + b2 )2
2-2         2-2      2    л 2 d        d b    а Poi = e 12 + e «2 + b2 + a2	4-2       7-2     2-2      ~2     2-2               2      2            4-2 dr     г      -d    г      _d         b     а             d-. e 12+«2 + 4e i2 + 4e «2 — 2^-y----^r2e 12+«2.   (11) b2           а2              (b2 + а2 )2

В исследуемом резонаторе радиус диафрагмы г д = 1, 05 мм, а ~ 0,493 мм, b ~ 0, 519 мм.

Результаты вычислений представлены в табл. 2.

Т а б л и ц а 2

Результаты вычислений

	P00	P10	P01
Численное вычисление	0,00019	0,0016	0,0024
Аналитическое вычисление	0,00019	0,002	0,0021

Для основной моды значения совпали, для поперечных мод различие составляет 20 %. Это говорит о том, что сделанные при разложении по маленькому параметру приближения довольно грубы для данного резонатора. Однако, поскольку производится оценка по порядку величины, допустимо использовать аналитические выражения.

5.    Эксперимент

Для экспериментального исследования спектра частот и потерь мод резонатора, а также его юстировки использовалась установка, блок-схема которой представлена на рис. 2.

Задающий лазер 1, в качестве которого выбран зеемановский кольцевой He-Ne лазер с длиной волны 0,6328 мкм типа К-5 [3], является источником излучения, которое попадает на поворотное зеркало 2, проходит через четвертьволновую фазовую пластинку 3 для получения круговой поляризации. С помощью плоскопараллельных пластин 4, отклоняемых в разных плоскостях, регулируется положение луча. Проходя через поляризатор 5, излучение становится поляризованным. После оно попадает внутрь резонатора 6 через сферическое зеркало и выходит через плоское зеркало на фотоприемник.

Изменением частоты излучения с помощью пьезокерамики на задающем лазере производится сканирование резонатора.

КФПУ

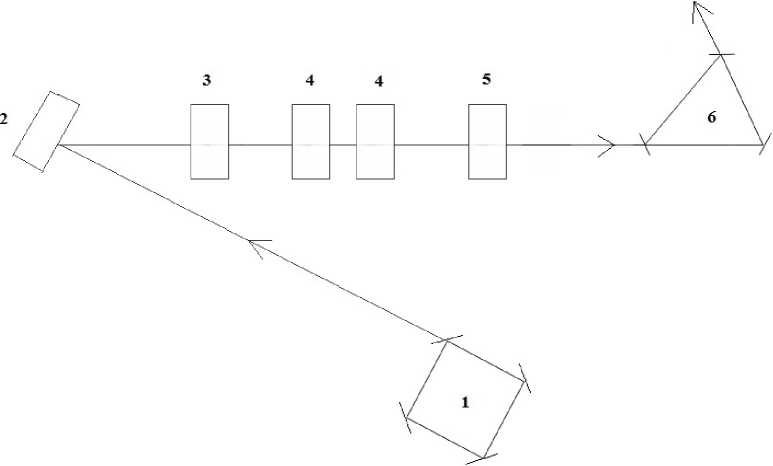
Рис. 2. Блок-схема установки: 1 — зондирующий лазер; 2 — поворотное зеркало; 3 — фазовая

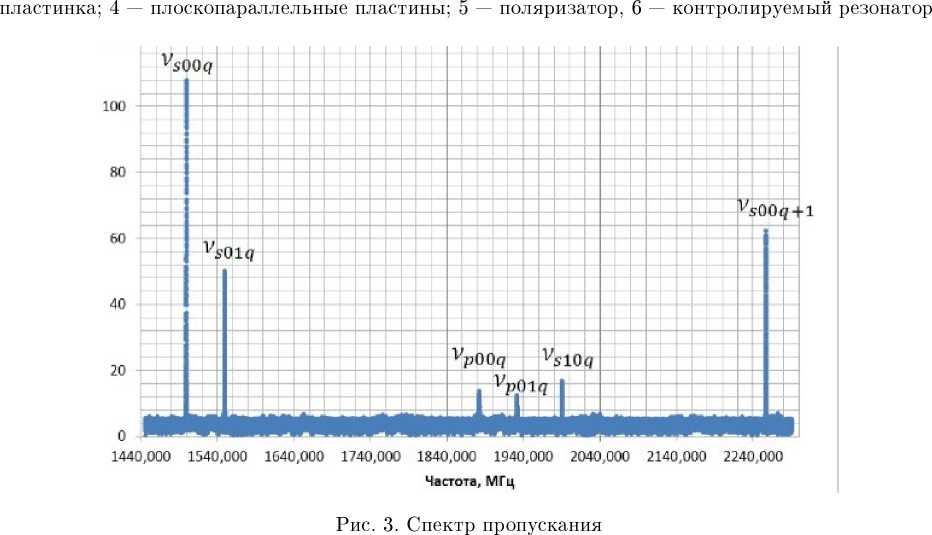
На рисунке 3 представлен спектр пропускания исследуемого резонатора. По нему были определены расстояния между различными модами резонатора и первой основной модой.

По исходным спектрам было видно, что ochobhbic моды расположены не эквидистантно. Это связано с нелинейноствю пьезокерамики, используемой в задающем лазере для изменения периметра резонатора и соответственно плавной перестройки длины волны выходящего излучения. Для уточнения значений расположения пиков был произведен пересчёт спектра с учетом нелинейности. На рисунке 3 представлен именно пересчитанный спектр.

Результаты измерения и расчёта межмодовых расстояний представлены в табл. 3. В спектре межмодовое расстояние s-поляризации определяется межмодовым расстоянием задающего лазера (757 МГц), т.к. его межмодовый частотный интервал уже, чем исследуемого лазера.

Т а б л и ц а 3

Значения межмодовых расстояний

Метод определения	Av m	AVg	Avn	AVa	Avp
Эксперимент	49 МГц	_	56 МГц	52 МГц	382,3 МГц
Теория	47 МГц	869 МГц	53 МГц	_	382,5 МГц

Фазовая анизотропия зеркал находится по формуле

Л        Av_a

Аср = 2л—— = 0, 38 рад.

AVg

Значительная фазовая анизотропия в эксперименте объясняется применением зеркал, предназначенных для работы под углом падения 44°.

На основе экспериментального спектра был выполнен анализ потерь мод резонатора. Для этого из спектра определялась полуширина линии на полувысоте. Расчёт потерь проводился по формуле

Av a = 2л    ,

AVg где Av — ширина спектральной линии, измеренная на уровне половины максимальной интенсивности, a Avg — межмодовое расстояние резонатора.

Измерения и юстировка резонатора выполнялись с использованием частично пропускающих плоских зеркал, обеспечивающих вывод излучения на фотоприёмник. Затем эти зеркала были заменены на штатные (глухие). Пересчёт величины потерь осуществлялся в предположении, что дифракционные потери остаются неизменными при замене плоских зеркал. Потери глухих зеркал измерялись отдельно. Полученные данные сведены в табл. 4.

Т а б л и ц а 4

Значения потерь

Номер моды	s00g	s10g	s01g
Потери экспериментальные с пропускающими зеркалами, %	0,145	0,197	0,250
Дифракционные экспериментальные потери, %	0,058	0,110	0,163
Потери экспериментальные с глухими зеркалами, %	0,093	0,145	0,198
Гасчётные дифракционные потери (первый метод), %	0,007	0,046	0,097
Гасчётные дифракционные потери (второй метод), %	0,019	0,161	0,239
Гасчётные суммарные потери (первый метод), %	0,042	0,081	0,132
Гасчётные суммарные потери (второй метод), %	0,054	0,196	0,274

6.    Заключение

Теоретическая модель, учитывающая фазовую анизотропию зеркал, демонстрирует хорошее соответствие с экспериментом.

Дифракционные потери основной моды резонатора (P_soo = 0, 058%) оказались на порядок больше потерь, рассчитанных по числу Френеля, и одного порядка с потерями, полученными с помощью предложенного в работе метода (P_soo = 0, 007% и P_soo = 0, 019% соответственно).

Дифракционные потери поперечных мод (P_sio = 0,11% и P_soi = 0,163%) оказались близки к рассчитанным P_s1o = 0,161 % и P_so1 = 0, 239% для второго метода. Для метода расчета потерь по числу Френеля аналогично основной моде имеется отличие на порядок P_sio = 0, 046% и P_soi = 0, 097%. Полученные результаты говорят о том, что предложенная оценка подходит для определения потерь мод резонаторов с малыми дифракционными потерями.

Рекомендуется выполнять предварительную юстировку резонатора для р-поляризации, а завершающую — для s-поляризации, что требует наличия в юстировочной системе функции изменения поляризации исходного лазерного излучения. Окончательные измерения оптических потерь и финальную настройку резонатора следует проводить для мод v_sooq и v_s1o_q s-полярпзаппп.