В данной статье использован метод спектрального разложения решения интегрального уравнения Линдли для систем массового обслуживания типа G/G/1 для нахождения среднего времени ожидания требований в очереди. Наиболее доступно для исследователей этот метод продемонстрирован в [1]. Важным моментом данного метода является конструирование спектрального разложения для рассматриваемой системы, а затем – нахождение нулей и полюсов этого разложения.

В русскоязычной научной литературе его аналогом является метод факторизации с использованием характеристических функций [2].

Настоящая статья посвящена анализу СМО E2/H2/1 по символике Кендалла с эрланговским и гиперэкспоненциальным входными распределениями второго порядка и является продолжением исследований [3–6]. В теории массового обслуживания исследования систем G/G/1 актуальны в связи с тем, что они активно используются в современной теории телетрафика при моделировании систем передачи данных различного назначения, к тому же нельзя получить решения для таких систем в конечном виде для общего случая.

Также использованы приемы и способы аппроксимации законов распределений методом моментов теории вероятностей [7–12]. Схожие результаты современных исследований по системам массового обслуживания приведены в работах [13–15].

Постановка и решение задачи

В исследовании ставится задача вывода решения по средней задержке требований в очереди в системе E2/H2/1 с эрланговским и гиперэкспоненциальным входными распределениями второго порядка как основной характеристики любой СМО.

Для системы E2/H2/1 законы распределения интервалов входного потока и времени обслуживания задаются функциями плотности вида a (t ) = 4X2 te -2X t,                                             (1)

b ( t ) = q Ц 1 e ^Ц 1 t + ( 1 - q ) ^ 2 e ^ц 2 t .                           (2)

Запишем преобразования Лапласа функций (1) и (2):

I 2X I

A ( s H йт, J •

B ( ⁵ ) = q -^ 1— ⁺ ( 1 ^- q )- ^ 2—.

^x       s + Ц 1 ^x       s + Ц 2

Выражение для спектрального разложения решения интегрального уравнения Линдли для системы E2/H2/1 примет вид

• V₊ ( s)           )2

A ( - s ) ■ B ( s ) - 1 =21112 = 1- 2^ I _x               (3)

• V - ( s ) ( 2 X- s J

  X

  
  

  q ¹

  Ц 1 + s

  
  

  ^{( 1} - q )

  
  

  ^ 2

  Ц 2 + s

  
  

  - 1 =

  
  

  - s ( s + s 1 )( s + s 2 )( s — s 3 )

  (2 X — s ) ( s + Ц 1 )( s + Ц 2 )

  т. к. многочлен четвертой степени в числителе выражения (3) можно представить в виде разложения — s ( s ³ — c 2 s ² — c 1 s — c 0 ) с коэффициентами c 2 = 4X — Ц 1 — Ц 2 , C 1 = 4 Х ( Ц 1 + Ц 2 — X ) — Ц 1 Ц 2 ,

  c 0 = 4X q ( Ц 1 — ^ 2 ) + 4 ХЦ 1 ( Ц 2 — X )].

  В свою очередь кубический многочлен

  s — c 2 s — c 1 s — c 0                                          (4)

  с такими коэффициентами имеет два действи-

  
  
  

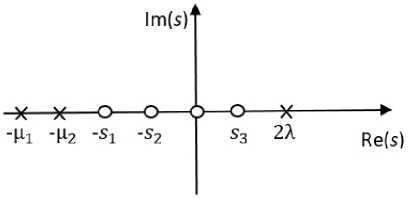
  Рис. Нули и полюсы функции у ( s ) / V ( s ) для системы

  E₂/H₂/1

  Fig. Zeros and poles У+ ( s ) / у ( s ) function for the E 2 /H 2 /1 system

  
  

  W * ( s ) = s -Ф + ( s ) =

  
  

  s 1 s 2 ( s + P 1 )( s + Ц 2 ) ( s + s 1 )( s + s 2 ) P 1 P 2

  
  
  
  

  тельных отрицательных корня — s 1 , — s 2 и один положительный корень s ₃ в случае стационарного режима, т. е. когда 0 < р = т ^ / Т х <  1, где р , Т х , Т_ц коэффициент загрузки, средний интервал поступлений и среднее время обслуживания в системе

  
  

  соответственно.

  
  

  Исходя из правил построения функций у₊ ( s ) и у ( s ) , из выражения (3) за функцию у₊ ( s )

  
  

  Производная от функции W ( s ) со знаком минус в т. s = 0 даст среднее время ожидания:

  dW ( s )         s 1 s 2 ( s + P 1 )( s + Ц 2 )

  j       I s =0= /                 \         I s =0 =

  ds            ( s + s 1 )( s + s 2 ) P 1 P 2

  1111 —--1------.

  s 1 s 2 Ц 1 H 2

  
  

  примем

  
  

  Окончательно среднее время ожидания в системе E₂/H₂/1 может быть определено из выражения

  
  

  V + ( ^s ) =

  
  

  s ( s + s 1 )( s + s 2 ) ( s + Ц 1 ) ( s + ц ₂) ’

  
  

  W — —+------ , ^s 1    ^s 2    P 1    P 2

  
  
  
  

  т. к. нули многочлена (4) s = 0, — s 1 , — s 2 и полюсы s = — P i , s = —Ц 2 лежат в области Re( s ) <  0. За функцию у_— ( s ) из выражения (3) примем

  
  

  ^V —^{( s ) —}

  
  

  (2 X — s ) ²

  ^{( s — s} 3 ) ’

  
  

  т. к. ее нуль s = 2 X и полюс s = s 3 лежат в области Re ( s ) > D .

  На рис. отображены нули и полюсы отношения у₊ ( s ) / V _ ( s ) на комплексной s -плоскости для исключения ошибок построения спектрального разложения. На рис. полюсы отмечены крестиками,

  
  

  где s 1 , s 2 - абсолютные значения отрицательных корней - s ₁, - s ₂ кубического многочлена (4) с приведенными выше коэффициентами, а ц^ Р 2 — параметры распределения (2). Таким образом, для среднего времени ожидания в СМО E₂/H₂/1 получено решение в замкнутой форме (6). Для того чтобы им воспользоваться в практических расчетах, необходимо определить неизвестные параметры распределений (1) и (2) через их

  
  

  а нули – кружками.

  Необходимая для получения решения константа равна

  К — lim V+l f > = 71i .

  s ^ 0 s     P 1 P 2

  
  

  числовые характеристики.

  Для распределения (1) запишем выражения для моментов: среднего интервала поступлений, второго начального момента, а через него для коэффициента вариации

  
  

  Тх — х , ТХ "

  х

  
  
  
  

  ^{c х —}72

  
  

  Далее строим преобразование Лапласа функции распределения вероятностей времени ожидания _Ф ( _s ) = K = ^s 1 ^s 2 ( ^s + P 1 )( ^s + P 2 )

  ^{+ V 7} V₊ ( s ) s ( s + s 1 )( s + s ₂ ) p 1 p ₂

  Откуда следует, что преобразование Лапласа функции плотности времени ожидания в системе E₂/H₂/1:

  
  

  Для распределения (2) воспользуемся свойством преобразования Лапласа воспроизведения момен-

  
  

  тов и запишем два начальных момента для распределения (2):

  V q + ' q , ^ — ^ + ^.       (7)

  ^и и. и.            ^и 2         2

  
  

  При аппроксимации с использованием первых двух моментов неизвестные параметры распреде-

  
  

Таблица. Результаты экспериментов для СМО E₂/H₂/1

Table. Experimental results for QS E₂/H₂/1