Спектральное решение для системы с запаздыванием с гиперэрланговскими распределениями

Для моделирования трафика современных сетей телекоммуникаций широко используются системы G/G/1 при частных законах распределений, т. к. не существует решения для таких систем в конечном виде для общего случая. Для исследования таких систем используют метод спектрального разложения решения интегрального уравнения Линдли, который наиболее доступно представлен в [1]. В русскоязычной научной литературе аналогом этого метода является метод факторизации с использованием характеристических функций [2].

Настоящая статья посвящена анализу СМО HE₂/HE₂/1 со сдвинутыми вправо от нулевой точки гиперэрланговскими (HE₂) входными распределениями второго порядка и является продолжением исследований [3–6]. В результате этого будем иметь новую СМО с запаздыванием во времени, которую обозначим через HE 2 /HE 2 /1 в отличие от обычной системы HE₂/HE₂/1, рассмотренной в [5].

В общем случае гиперэрланговский закон распределения порядка R задается плотностью и обозначается HER [1]. Гиперэрланговское распределение представляет собой вероятностную смесь нормированных распределений Эрланга порядка k с функцией плотности вида fk (t) =

k X( k X t)k-1 e _ kxt (k -1)!   e и является наиболее общим распределением неотрицательных непрерывных случайных величин, поскольку имеет коэффициент вариации cт в интервале от 0 до ∞ [8].

В данной работе мы ограничимся гиперэрлан- говским распределением второго порядка при k, = 2 с функцией плотности f (t) = 4 p X2 te 2/" t + 4 (1 - p) X2 te -2X22

в связи с тем, что при k , >  3 дальнейшие выкладки становятся чрезвычайно трудоемкими.

Для системы HE 2 /HE 2 /1 интервалы поступлений и времени обслуживания описываются функциями плотностей сдвинутых вправо от нулевой точки гирерэрланговских законов распределений второго порядка:

f ⁽ t ) =

R J z « ,

i

k i ^X i ( k i ^ it^k i ^{- 1} e - k, x f

( k , - 1 )!               ^,

t >  0 ;

0 ,

t <  0 ,

R

E « , = 1 i = 1

a ( t ) = 4 p X 2 ( t - 1 0 ) e ^{2 X} 1 ⁽ t t ⁰ ) +                              (1)

+ 4 (1 - p )X2 (t -10) e -TX2(t- t0 ’, b (t) = 4qц2 (t -10 )e-2Ц1(t-t0 ’ +                             (2)

+ 4 ( 1 - q ) ц 2 ( t - 1 0 ) e "^2ц2⁽ t ^- t ⁰ ’ ,

где t о >  0 - параметр сдвига закона распределения.

Кроме метода спектрального решения в статье использован опыт аппроксимации законов распределений [7–12]. Результаты современных исследований по системам массового обслуживания приведены в работах [13–15].

1. Постановка и решение задачи

В статье ставится задача нахождения решения для задержки требований в очереди в СМО НЕ2 /НЕ— /1. Вкратце решение интегрального уравнения Линдли методом спектрального разло- жения состоит в нахождении для выражения

A ( - s ) ■ B (s ) - 1

v+GO

^V -⁽ s )

представления в виде произведения двух множителей, которое давало бы рациональную функцию от s. Здесь A (s) и B (s), соответственно, преобразования Лапласа функций плотности распреде- ления интервалов входного потока a(t) и времени обслуживания b(t), v+ (s) и v- (s) компоненты спектрального разложения – некоторые рациональные функции от s, которые можно разложить на множители.

Преобразования Лапласа функций (1) и (2) будут соответственно:

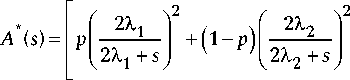
— t^s e ⁰

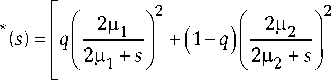
— t^s e ⁰

Тогда спектральное разложение решения интегрального уравнения Линдли для рассматриваемой системы

V, ( s)

A ( - s ) ■ B (s ) - 1        ' )

^v -^{( s} )

примет вид

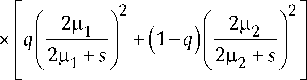
Выражение (3) получено на основании теоремы о запаздывании в теории преобразования Лапласа. Здесь показатели степени у экспонент с противоположными знаками в спектральном разложении обнуляются, и таким образом операция сдвига во времени нивелируется. Следовательно спектральные разложения решения интегрального уравнения Линдли для системы со сдвинутыми распределениями HE₂ /НЕ 2 /1 и для обычной системы HE₂/HE₂/1 будут идентичными. Тогда мы можем использовать результаты, полученные в [5] для обычной системы HE₂/HE₂/1, и сразу записать компоненты спектрального разложения, не повторяя выкладки в [5]:

s ( s + s )( s + s )( s + s ₃)( s + s ) v + ( s ) =------- ¹------- 2------- ³ „ 4 ,                     (4)

[( s + 2 ц 1 ) ² ( s + 2 ц 2 ) ² ]

^{(2 X}1 ^- s ^{) 2 (}2X₂ ^- s ^{) 2}

• V - ( s ) =-- .

• ^{2 2}     ( s - s 5 )( s - s 6 )( s - s 7 )

В выражениях (4) -s 1, -s2, -s3, -s4 - корни многочлена (5) седьмой степени с отрицательными вещественными частями, а s5, s6, s7 - корни с положительными вещественными частями. Многочлен в числителе разложения (3), содержащий 92 слагаемых после приведения подобных членов, имеет вид s7 - c6s6 - C5s5 - c4s4 - c3s3 - c2s2 - c 1 s - c0 (5) и собран с помощью символьных операций Mathcad. Его коэффициенты:

c 0 = a 0 b - a 1 b 0 - 256 X 1 X 2 ^ 1 ^ 2 x (6)

x [X1X2 (^1 + Ц2) Ц1Ц2 (X1 + X2)], c 1 = a0b2 - a1 b1 + a2 b0 - 64[X1 X2 (ц1 + Ц2) +

+ Ц1Ц2 (X1 + X2)] - 256X1X2 Ц1Ц2 x x (X1X2 - X^ - Х1Ц2 - Х2Ц1 - Х2Ц2 + Ц1Ц2), v+(s) v-(s )

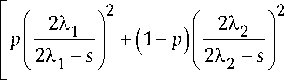
ts e 0 x

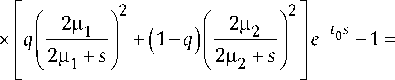
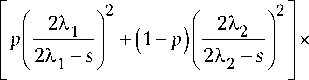
c2 = a2b1 - a 1 b2 - 64{[X1 X2 + Ц1Ц2 (X1 + X2)] x x (Ц1 + Ц2) - (X1X2 + X1X2 )(ц1 + ц2) +

+ Ц 1 Ц 2 ( X 1 + X 2 )]} + 256 X 1 X 2 ^ 1 ^ 2 ( X 1 + X 2 -Ц 1 -^ 2 ), c 3 = a 2 b 2 - 16 [ X 1 X 2 + Ц 1 Ц 2 + ( X 1 + X 2 )( Ц 1 + Ц 2 )] +

+ 64 [( X 1 + X 2 )( Ц 1 + Ц 2 )( X 1 X 2 + Ц 1 Ц 2 ) -

- X 1 X 2 ( Ц 1 + Ц 2 ) - ^ 1 ^ 2 ( X 1 + X 2 ) - 4 X 1 X 2 Ц 1 Ц 2 ],

c 4 — 16[(X1 + X2 )(X1X2 + 4ц^ ) — (Ц1 + Ц2) x x (Х1 + X2 + 4X1X2 + Ц1Ц2) + (Xi + Х2 )(Ц1 + Ц2)], c 5 — 16[(Xi + Х2 )(Ц1 + Ц2) — Х1Х2 —

• — Ц 1 Ц 2 — 4 ( X i + X 2 + Ц 1 + Ц 2 )],

c 6 — 4 ( X 1 + X 2 — Ц 1 — Ц 2 ).

Коэффициенты (6) для сокращения их записи содержат промежуточные параметры:

a 0 — 16X2x2 ,   a 1 — 16X1X2 [ p X1 +(1 — p )X2 ], a 2 — 4[ p X2 +(1 — p )X2 ], b 0 — 16ц2ц2,

• b 1 — 16 ц 1 ц ₂ [ q ц ₁ + ( 1 — q ) ц ₂ ],

b 2 ^— 4^[ q ^ 1 + ( 1 ^— q ) ^ц 2 ^] .

И все они зависят от параметров распределений (1) и (2).

Исследование многочлена числителя разложения, нахождение его нулей, а также полюсов разложения – это главное в спектральном решении интегрального уравнения Линдли. Далее по методике спектрального разложения определим постоянную

• V, ( s)

K — lim s ^0 s

• _— lim ( s + s 1 )( s + s 2 )( s + s 3 )( s + s ₄ ) _— s 1 s 2 s 3 s 4

^s ^ 0     ( s + 2 Ц 1 ) ² ( s + 2 ^ 2 ) ²         16 ц 2 ц 2

Через нее определяем преобразование Лапласа

ФРВ времени ожидания

^Ф + ( s ) ^— KM ^—

Ms)

s 1 s 2 s 3 s 4 ( s + 2 Ц 1 ) 2 ( s + 2 ^ 2 ) ²

16 Ц 1 ц 2 s ( s + s 1 )( s + s 2 )( s + s 3 )( s + s 4 )

Тогда преобразование Лапласа функции плотности времени ожидания будет

W * ( _s ) _—      ^s 1 ^s 2 ^s 3 ^s 4 ^{( s} + 2 Ц 1 ^{) 2 ( s} + 2^^{) 2}      ,           (7)

16 Ц 2 Ц 2 ( s + s 1 )( s + s 2 )( s + s 3 )( s + s 4 )

а его производная со знаком минус в т. s — 0 дает среднее время ожидания dW * (s) ds

s = 0