Спектральные характеристики интегрального оператора внутренней задачи электродинамики для эллиптической рамочной структуры
Автор: Табаков Д.П., Майоров А.Г.
Журнал: Физика волновых процессов и радиотехнические системы @journal-pwp
Статья в выпуске: 1 т.26, 2023 года.
Бесплатный доступ
Статья посвящена анализу электродинамических свойств эллиптической рамочной структуры. С учетом двойной симметрии внутренняя задача для рассматриваемой структуры в рамках тонкопроволочного приближения сведена к четырем интегральным уравнениям Фредгольма первого рода, записанным относительно независимых токовых функций. Проведено исследование спектральных характеристик интегральных операторов соответствующих интегральных уравнений для различных значений электрической длины и коэффициента эллиптичности рамки. Показано, что собственные функции интегральных операторов при близких значениях указанных параметров имеют высокую степень корреляции и по форме близки к тригонометрическим функциям. Выявлены особенности частотной зависимости собственных значений интегральных операторов. Сделан вывод о резонансном характере этих зависимостей, что делает эллиптическую рамочную структуру во многом схожей с рассмотренными авторами ранее трубчатым вибратором и сферической спиральной частицей. Результаты, представленные в статье, способствуют формированию углубленного понимания процессов, протекающих в рассматриваемой структуре, а также служат ориентиром при построении аппроксимационных моделей решения внутренней задачи.
Эллиптическая рамочная структура, рамочная антенна, интегральное представление электромагнитного поля, распределение тока, интегральное уравнение, собственные функции, собственные значения
Короткий адрес: https://sciup.org/140297876
IDR: 140297876 | УДК: 537.862 | DOI: 10.18469/1810-3189.2023.26.1.58-69
Текст научной статьи Спектральные характеристики интегрального оператора внутренней задачи электродинамики для эллиптической рамочной структуры
Рамочные антенны являются одним из наиболее распространенных типов антенн. Они имеют широкую сферу применения (телевидение, сотовая связь, радиосвязь и т. д.). Их теоретическое исследование осуществлялось в течение довольно длительного времени, поэтому сейчас имеется довольно большое количество научных работ по данной тематике. В настоящий момент расчет характеристик подобных структур можно осуществлять с высокой степенью точности, привлекая системы автоматизированного проектирования (САПР), с помощью инженерных формул, а также предлагаемых в различных работах моделей, имеющих различную степень сложности. В [1] анализ рамочной антенны осуществляется в приближении равномерного распределения тока. В [2] для расчетов используется теория длинных линий. В [3; 4] в поперечном сечении проводника, имеющего малые волновые размеры, для распределения тока вводится квазистатическое приближение. В [5] рассмотрена кольцевая полосковая антенна, для которой сформулирован бесконечный набор систем СИУ относительно Фурье-гармоник компонент вектора поверхностной плотности тока на полоске. Приведенные результаты позволяют оценить соотношение между амплитудами продольной и поперечной компонент тока.
Следует отметить, что строгие математические модели разработаны по большей части только для кольцевых рамок, имеющих наиболее простую геометрию. Присутствующая в этом случае осевая симметрия структуры существенно упрощает решения внутренней задачи. Строгие модели рамок более сложной конфигурации (эллиптические, многоугольные и т. д.) не так сильно распространены, поэтому создание подобных математических моделей представляет собой актуальную задачу. Даже в случае строгих моделей, формулируемых в виде ИУ (в том числе сингулярных), авторы, как правило, ограничиваются анализом количественных характеристик распределений тока, не углубляясь в причины, приводящие к формированию этих распределений. Указанный момент является ключевым при создании адекватной картины внутренних физических процессов в рассматриваемых структурах. Решение этой задачи можно осуществить на основе метода собственных функций (МСФ), предложенного в [6]. Ранее этот метод был применен авторами к анализу и построению аппроксимации решения внутренней задачи для трубчатого электрического вибратора [7; 8]. Альтернативой МСФ является метод характеристиче-
Е^^в © Табаков Д.П., Майоров А.Г., 2023
ских мод [9–11]. Среди его достоинств в сравнении МСФ можно отметить простоту численной реализации, но существенным недостатком этого метода является низкая устойчивость вычислительной процедуры.
В данной статье рассмотрена математическая модель эллиптической рамочной структуры (ЭР), сформулированная в виде четырех независимых ИУ. Решение внутренней электродинамической задачи сформулировано на основе МСФ. Способ возбуждения ЭР не конкретизировался в целях повышения общности представляемых результатов, т. е. предложенную модель можно использовать для решения как антенных, так и дифракционных задач. В заданном диапазоне частот для различных вариантов геометрии ЭР проведен анализ спектральных характеристик интегральных операторов (ИО) соответствующих ИУ.
1. Постановка задачи
Рассмотрим решение внутренней задачи электродинамики на эллиптической рамочной структуре (ЭР) методом собственных функций. Геометрия структуры показана на рис. 1. Проводник ЭР, обладающий бесконечно большой проводимостью, имеет круглое сечение диаметра 2 ε , которое много меньше длины волны λ и полной длины L образующей проводника. Таким образом, для ЭР целесообразно использовать тонкопроволочное приближение, в рамках которого объемная плотность тока сводится к азимутально независимому полному току, протекающему по образующей проводника. Символ L далее будет использоваться также и для обозначения образующей.
Параметрическое уравнение образующей L ЭР имеет вид
r(t) = rxcostxˆ +rysintˆy, t∈[0;2π]. (1) Здесь t – параметр, являющийся по сути азимутом цилиндрической либо сферической системы координат; rx и ry – большая и малая полуоси эллипса соответственно. Натуральный параметр на спиралях определяется выражением t l(t)=∫ 0
d r ( t ) dt
t dt′=rx ∫sin2t′+κcos2t′dt′, 0
здесь κ = ry / rx ≤ 1 – коэффициент эллиптичности. В натуральном параметре уравнение образующей спирали будет определяться выражением (1) после замены t = t ( l ). Функция t ( l ) определяется численно из (2) методом обратной интерполяции. Длина образующей ЭР определяется как L = l (2 π ) =
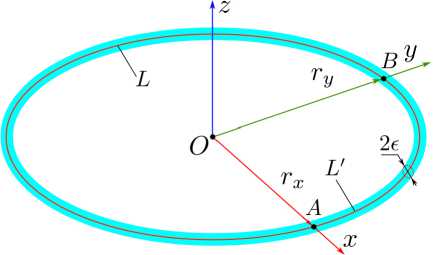
Рис. 1. Тонкопроволочная модель эллиптической рамочной антенны
Fig. 1. Thin-wire model of an elliptic frame antenna
= 4 rxE (1 -κ 2 ), в котором E ( x ) – полный эллиптический интеграл второго рода [12]. Минимальное значение радиус кривизны ρ min образующей L ЭР имеет в точках, соответствующих t =0 и t = π : ρ min = rx κ . Данное равенство требует наложения дополнительного условия на радиус проводника: £ < r x К .
В рамках принятой модели ЭМП структуры бу- дет описываться интегральным представлением (ИП), подробно представленным в [13]:
F ( r )= ∫ I ( l ′ ) K ( F )( r , r ( l )) dl ′ , F ≡ E , H ;
здесь: K ( F ) – ядра интегрального представления; I ( l ) – распределение полного тока на образующей проводника; r – радиус-вектор точки наблюдения. Корректность и достоверность результатов, получаемых с помощью ИП ЭМП (4), подтверждается в [14; 15].
Рассматриваемая структура при κ <1 обладает двойной зеркальной симметрией относительно плоскостей XOZ и YOZ , поэтому ее можно разбить на четыре идентичные части, образующие Ln ≡ L ′ которых описываются общим выражением вида:
r n ( t )= sn ( x ) rx cos t x ˆ + sn ( y ) ry sin t ˆ y , t e [0; n /2], n = 1...4.
{ s 1 ( x ), s 1 ( y )}={1,1}; { s 2 ( x ), s 2 ( y )}={ - 1,1};
{ s 3 ( x ), s 3 ( y )}={ - 1, - 1}; { s ( 4 x ), s ( 4 y )}={1, - 1};
В этом случае
F ( r ) = I ( l ′ ) K ( F )( r , r ( l ′ )) dl ′ , (4)
L ′ nn
F . E, H ; n .1 ^ 4.
Здесь In ( l ) – распределение тока на соответствующей образующей. Поставим граничное условие вида
( E (in)( r ( l )) + E ( r ( l ))) ⋅ ˆ l ( l ) =0
на каждой образующей и в результате получим систему ИУ следующего вида:
EjL.*n (l') Km, n (l'1') d1' = Em (1), n=1
m = 1 ™ 4, 1 e L = L /4.
Здесь
E m ( 1 ) = - l m ( 1 ) • Е 1М( Г п ( 1 ))' (5)
Km. n ( 1 ' 1 ') = l m ( 1 ) ' K E ' ( ' m ( 1 )' ' n ( 1 '»
- касательные составляющие стороннего электрического поля на образующих и ядра системы ИУ соответственно. В силу симметрии структуры имеют место равенства:
K m , m = K 1 , K m ,5 - m = K 4 ' m = 1 ™ 4;
K 1,2 = K 2,1 = K 3,4 = K 4,3 = K 2 ;
K 1,3 = K 3,1 = K 2,4 = K 4,2 = K 3 .
Для функций E m , I m и K m справедливы преоб-
|
разования вида 1 4 |
|
F m =2 Е w m ' n F n ' (6) |
|
n =1 |
|
4 |
|
F m =2 Е W m ' n F n ' F = E ' I ' K ' |
|
2 n =1 |
|
в которых wm , n – элементы матрицы Уолша: |
|
( 1111 1 |
|
11 - 1 - 1 |
|
W = . |
|
1 - 1 - 1 1 |
|
1 - 11 - 1 V J |
Относительно функций E m и I m исходная система ИУ распадается на 4 независимые подсистемы:
E m ( 1 '= i n ( 1 ^Km ( 1 ' 1 . ') d\ m = 1 ™ 4' 1 e L' (7)
m l m m
Физически плоскости XOZ и YOZ представляют для рассматриваемой структуры электрическую либо магнитную стенку поэтому для функций I i и их производных I’i справедливы следующие граничные условия:
I '1 'O) = I '1 ( L ' ) = 0; ^(0) = I '2 ( L ' ) = 0; (8)
Гз(0) = I 3( L ' ) = 0; ^(0) = I 4 ( L ' ) = 0.
Аппроксимируем образующие Li ломаными L(iN), имеющими N сегментов равной длины А. В рамках метода моментов в качестве базис- ных используем постоянные в пределах сегмента функции, а в качестве тестовых – дельта-функции, локализованные в центре сегмента. В результате получим 4 независимые СЛАУ, имеющие общий вид
Z ˆ I = E . (9)
В которых Z = Z ( m ) - матрицы моментов с элементами z m ); I = I ( m ) - векторы комплексных амплитуд токов I ( j m ) на сегментах; E = E ( m ) – векторы, содержащие значения функций стороннего поля E ( j m ) в центрах сегментов:
1 i +А /2
z im )=2 j k mN )( 1 i ' 1 'du ''
1 i -А /2
I ( j m ) = Im ( lj *), E ( j m )= Em ( lj *);
здесь 1i =( 1i+1 + 1i)/2 - значения натурального параметра в центрах сегментов; 1i - значения нату- рального параметра на границах сегментов; верхний индекс «N» в ядрах Km указывает' что в Km n, описывающихся вторым выражением (5), вместо исходных образующих rm(1) используются их линеаризованные аппроксимации rm(N)(l). Далее при отсутствии необходимости индекс m для матриц и векторов будем опускать.
Полная проблема собственных значений (СЗ) для матрицы Z формулируется следующим образом:
^ ^ ^ ^
ZJ = XJ .
В данном выражении ˆ J – матрица, столбцы J i которой являются собственными векторами (СВ) Z ˆ, при этом все СВ имеют единичную норму: | J n |= 1; X ˆ – диагональная матрица, диагональные элементы которой ^ ц = ^ i e X являются собственными значениями Z . Здесь следует отметить, что СЛАУ (9) эквивалентна ИУ (7) с вырожденным ядром' вычисляемым для сегментированных образующих, а СВ J n аппроксимируют собственные функции (СФ) Jn ( 1 ) интегрального оператора задачи (7). Решение полной проблемы собственных значений для комплексных матриц представляет собой стандартную задачу линейной алгебры, решаемой на основе QR-алгоритма [16]. Решение СЛАУ при известных ˆ J и X ˆ будет иметь вид
I = ( JX i 1 J T ) E .
Индекс « T » соответствует операции транспонирования. Матрица X является диагональной' поэтому вычисление обратной матрицы не представляет особых проблем. С физической точки зрения исследование зависимостей СВ и СЗ от частоты и параметров структуры представляет собой особый интерес, т. к. они в большей части определяют характер решения внутренней задачи. Также эти исследования служат основой для построения аппроксимационных моделей решений [8].
В нашем случае в качестве главного параметра, нормируемого к длине волны, следует выбрать длину образующей L ЭР: х = L / X . В качестве второго параметра будем использовать коэффициент эллиптичности к . Третий нормированный параметр – отношение радиуса провода ε к длине образующей L ЭР – в силу перечисленных ранее условий не оказывает существенного влияния на решение внутренней задачи, поэтому будем полагать, что ε / L = const.
Здесь также следует отметить, что при κ =1 ЭР обладает осевой симметрией, а собственные функции интегрального оператора могут быть выражены через пару соответствующих тригонометрических функций. При этом форма собственных функций не зависит от L / λ .
2. Численное моделирование и анализ результатов
Решение задачи (10) осуществлялось в прямоугольной области:
-
5 : X е x :[ X min ; X max 1, ке к :[ K m in; ^ ].
На интервалах x и κ вводились равномерно Nf узлов x f и N r узлов к r соответственно, в паре образующие множество точек { x f , к r } е 5. В расчетах полагалось, что x min =0, 01, x max =5, κ min =0,5, κ max=1, Nf =500, Nr =11.
Число сегментов N при линеаризации образующей полагалось равным 100, отношение ε / L ′ при этом было выбрано равным 3/250 с целью выполнения условия 2 s < А < 12 s [17], необходимого для обеспечения устойчивого решения СЛАУ в рамках выбранной системы проекционных функций. При этом ρ min / L ′ при κ =0,5 составляет примерно 0,4, что соответствует ранее обозначенному условию s ^ P min .
Вычисление СЗ X и СВ J осуществлялось с помощью процедуры ZGEEV [18], входящей в библиотеку с открытым исходным кодом LAPACK [19]. Важным моментом при проведении диапазонных вычислений в области 5 является отслеживание номеров СВ и СЗ [20; 21], так как при разных значениях x и κ процедура ZGEEV располагает СВ и СЗ в возвращаемых массивах различным образом. Поэтому непосредственное вычисление СВ и СЗ на практике необходимо дополнять алгоритмом их отслеживания и сортировки, а также алгоритмом корректировки знака СВ. При получении результатов для данной статьи использовался корреляционный алгоритм. Ранее он также применялся в [6], но, к сожалению, не был описан под- робно вследствие ограниченного объема статьи. В данной статье мы восполним этот пробел.
Пусть J ( X f* , к r* ) - матрица СВ, которую мы принимаем за образец; J ( x f , к r ) - матрица, нуждающаяся в сортировке СВ и корректировке из знаков. Существенным моментом здесь являются условия:
2| Xf —х* |/|Xf + х* |< 1; (11) 2 | кf — к ^ * | /1 к f + к ^ * |^ 1, то есть вычисления необходимо проводить для матриц, расположенных в близких точках области 5, что обеспечивает высокую степень корреляции СВ. В случае удаленных точек СВ с одними и теми же индексами могут иметь низкую степень корреляции и сильно отличающуюся форму. Для коррекции номеров и знаков СВ необходимо вычислить корреляционную матрицу:
K = J ( X f* , к r* ) J ( X f , к r ).
Далее осуществляется нормирование каждой строки K ˆ к элементу соответствующей строки, имеющему максимальное по модулю значение. После этой процедуры в каждой строке K ˆ будет содержаться один элемент k i j , имеющий значение 1 или –1, значения остальных элементов при условии (11) будут по модулю существенно меньше единицы. Столбцу с индексом i откорректированной матрицы J ( X f , к r ) будет соответствовать j -й столбец исходной матрицы J ( xf , κ r ), умноженный на скаляр ki , j (корректировка знака). Позиция элемента ki , j также используется для корректировки номеров СЗ вектора X ( xf , κ r ) (без корректировки знака): здесь i - позиция в скорректированном векторе СЗ; j - позиция в исходном векторе СЗ. После корректировки матрицу J ( X f , к r ) можно принять за образцовую ( X f ^ X f * ; к r ^ к r* ) и повторить процедуру для матрицы J , вычисленной в новой точке области 5, удовлетворяющей условию (11).
В нашем случае в качестве образцовой была принята матрица ˆ J ( x 1, κ 1). На первом этапе были скорректированы матрицы ˆ J ( x 1, κ r ) и векторы X ( x 1 , к r ) для r = 2... N r . На втором этапе скорректированные матрицы использовались для коррекции матриц J ( X f , к r ) и векторов X ( x f , к r ) для соответствующего индекса r ( r = 2 . N f ).
Численные расчеты преследовали две цели. Первая цель, имеющая преимущественно прикладное значение, связана с определением возможностей построения аппроксимационной модели решения внутренней задачи на основе МСФ.
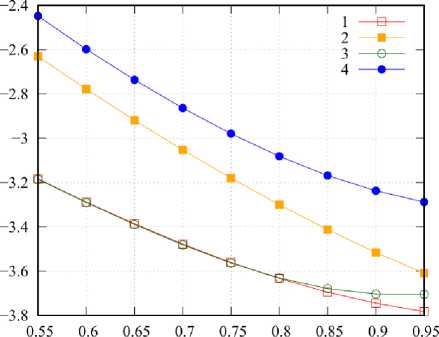
а
Рис. 2. Зависимость р r от к r ; а - x = 0,01; б - x = 5, номер кривой соответствует номеру СЛАУ
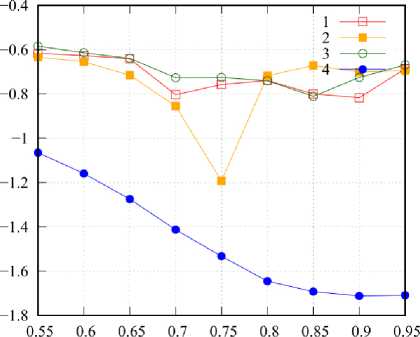
б
Fig. 2. Dependence р r on к r ; a - x = 0,01; b - x = 5, the number of the curve corresponds to the number of SLE
а
Рис. 3. Зависимость
Fig. 3. dependence рf рf от x on x*f ;
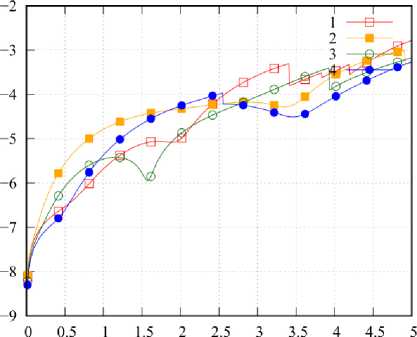
f; а - к = 0,95; б - к = 0,5, номер кривой соответствует номеру СЛАУ a - к = 0,95; b - к = 0,5, the number of the curve corresponds to the number of SLE
Для достижения указанной цели возникает необходимость решения ряда задач. Первая задача заключается в анализе степени корреляции СВ, вычисленных в различных точках области 5. Эта информация необходима для определения возможности построения аппроксимации матриц СВ в указанной области. Вторая задача связана с анализом форм СФ J n ( l ), определяющихся результатом интерполяции соответствующих столбцов матриц J , при этом в качестве узлов интерполяции выступают точки коллокации l; , i = 1... N . По результатам данного анализа можно определить системы функций, наиболее подходящих для аппроксимации собственных функций в виде соответствующих рядов. Третья задача связана с анализом поведения СЗ в области 5. Данный анализ, как и в случае СВ, позволяет определить системы функций, наиболее подходящих для аппроксимации СЗ для различных точек 5.
Вторая цель имеет преимущественно теоре- тическое значение и связана с определением характера частотной зависимости СЗ. Ранее в [6; 7] для других структур уже было показано, что эта зависимость имеет резонансный характер, поэтому основной вклад в формирование решения внутренней задачи вносит лишь небольшая часть СФ. В данном случае нам необходимо подтверждение этого факта с некоторыми дополнительными деталями для рассматриваемой структуры. Для оценки невязки векторных либо матричных массивов V, вычисленных в паре точек области 5, будем использовать общую формулу:
res( V ; x , к ; x , к ) = lg
| V ( x , к ) - V ( x , к )|
| V ( x , к ) + V ( x , к )| )
На рис. 2 приведены графики значений р r = = res( J ; x , к r + 1 ; x , к r ) для случая x = 0,01 ( а ) и случая x =5 ( б ). Вдоль оси абсцисс отложена величина
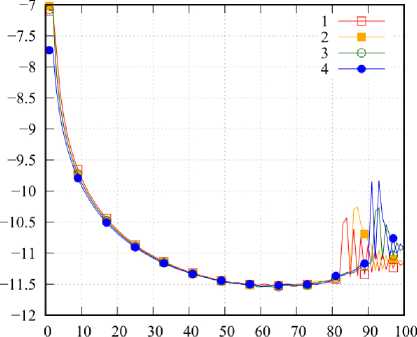
f = 1; к = 1
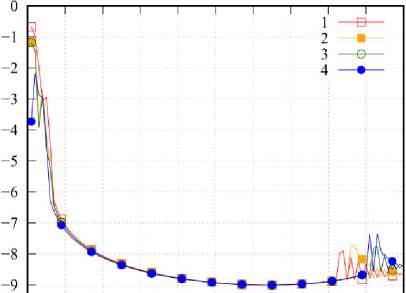
1 о L---------------1------------------1------------------111------------------1------------------1------------------1------------------1------------------
О 10 20 30 40 50 60 70 80 90 100
f = 499; к = 1
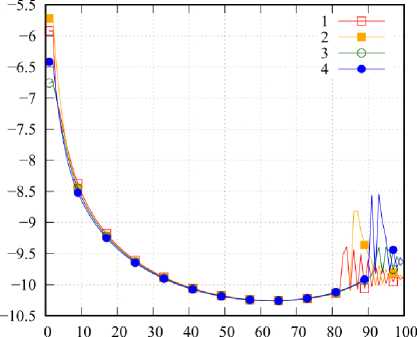
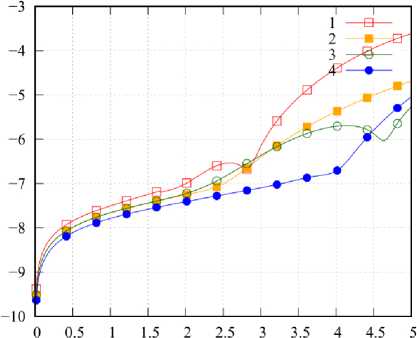
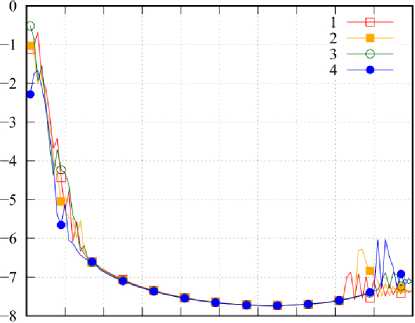
Рис. 4. Зависимость p n от n , номер кривой соответствует номеру СЛАУ
Fig. 4. Dependence p n on n , the number of the curve corresponds to the number of SLE
0 10 20 30 40 50 60 70 80 90 100
f = 499; к = 0,5
кr = ( к r + 1 + к r )/2. Видно, что значения невязки для разных m заметно отличаются, при этом невязка возрастает с уменьшением к и с увеличением x , но в целом для довольно малого значения N r результаты можно считать довольно хорошими. Уменьшить невязку можно путем уменьшения расстояния между узлами вблизи к т^. При x , находящихся вблизи x max , этого будет недостаточно. Здесь необходимо также увеличение Nr .
На рис. 3 приведены графики значений pr = = res(J; xf+1, к; xf, к) для случая к = 0,95 (а) и случая к = 0,5 (б). Вдоль оси абсцисс отложена величина xf = (Xf+1 + Xf)/2. Здесь можно отметить, что значения невязки существенно меньше, чем в рассмотренном ранее случае, но при этом существенно выше и ее разброс: минимального значения она достигает при x = xmin, максимального - при x = xmax. Для уменьшения разброса невязки следует использовать неравномерное расположение узлов xf , расстояние между которыми должно уменьшаться с ростом x . В целом следует сказать, что определение расположения опорных точек при заданном значении невязки представляет собой самостоятельную и довольно интересную вычислительную задачу, имеющую важное прикладное значение.
На рис. 4 приведены графики значений p n = = res( J n ; x f + 1 , к ; x f , к ), детализирующие невязку по x для различных номеров n СВ в угловых точках области 5. Вдоль оси абсцисс отложен номер СВ. Из представленных графиков видно, что наибольший вклад в ранее рассмотренные значения невязки вносят СВ с небольшими значениями номеров n , что является хорошим ориентиром при построении аппроксимаций СВ в области 5.
На рис. 5 приведены графики действительной и мнимой части первых четырех собственных функций, вычисленных при x = 5, к = 0,5. Видно, что они соответствуют условиям (8). Очевидно, что СФ могут быть достаточно просто аппроксимированы быстро сходящимися рядами тригонометрических функций. Также можно отметить, что в случае к = 1 функция J 1 ( l ) имеет равномерное распределение, а при к = 0,5 равномерность на-
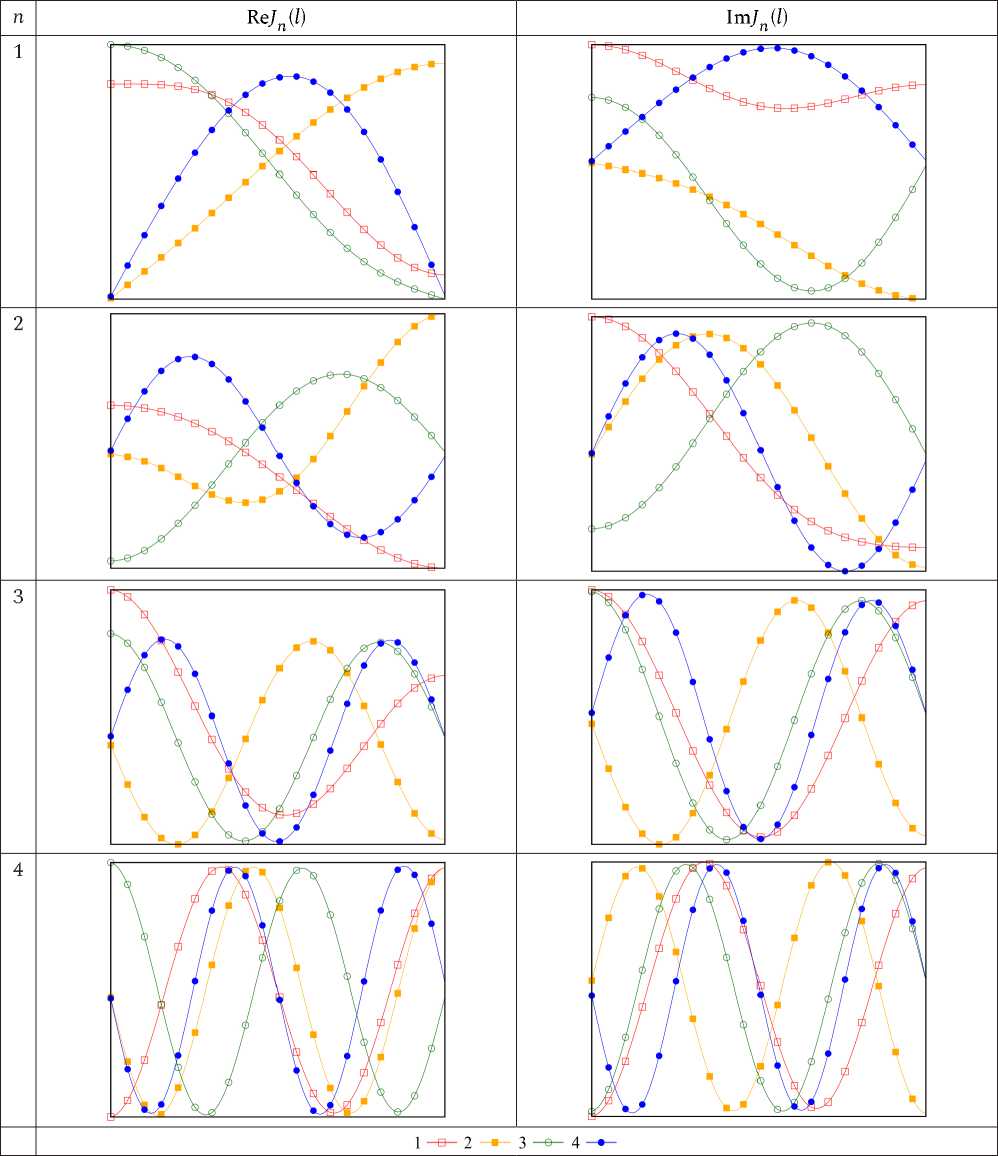
Рис. 5. Вид первых четырех собственных функций J n ( l ); x = 5, к = 0,5, номер кривой соответствует номеру СЛАУ
Fig. 5. View of the first four of its own functions J n ( l ); x = 5, к = 0,5, the curve number corresponds to the number of SLE
рушается, а ее максимум смещается к точке, имеющей меньший радиус кривизны.
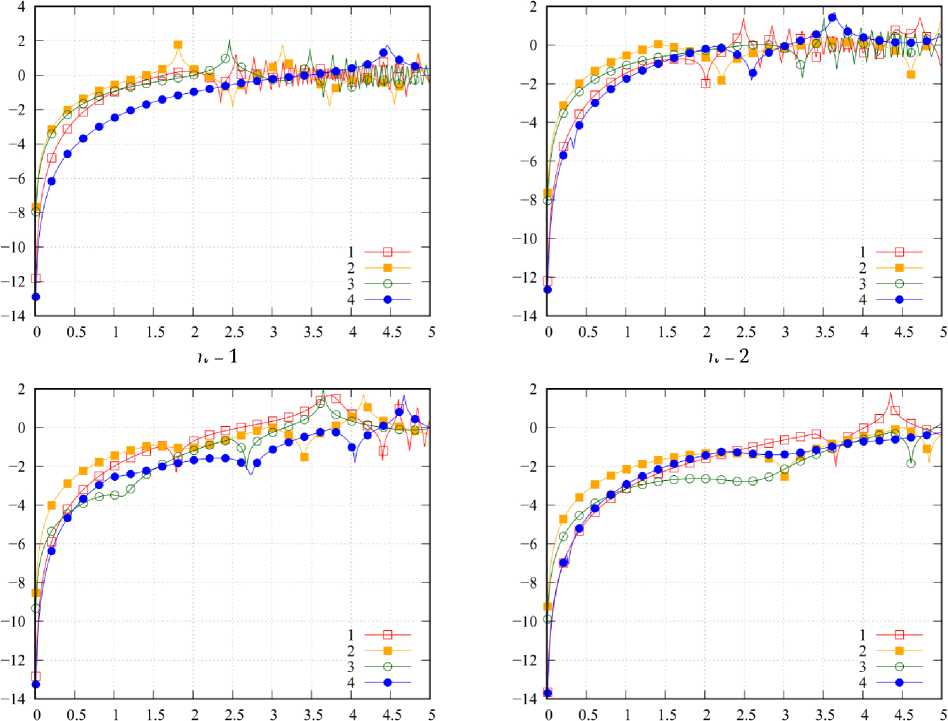
Соотношение интенсивностей действительной и мнимой части собственных функций позволяет оценить величина Zn(x) = | ImJn(x)| /| ReJn(x) |, графики которой приведены на рис. 6. Во всех случаях наблюдается общая тенденция: при малых значе- ниях x интенсивность мнимой части собственных функций мала, поэтому колебания точки СФ происходят практически синфазно. С ростом x интенсивность действительной и мнимой части становятся соизмеримыми, что ведет к нарушению синфазности колебаний. Также при больших значениях x есть точки, в которых интенсивность
n =1
n =2
n =4
n =3
Рис. 6. Зависимость ζ n от x ; κ =0,5, номер кривой соответствует номеру СЛАУ
Fig. 6. Dependence ζ n on x ; κ =0,5, the number of the curve corresponds to the number of SLE
мнимой части СФ в десятки раз превышает интенсивность действительной части.
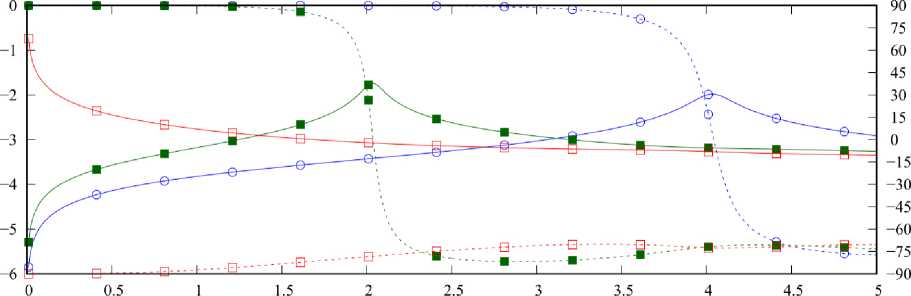
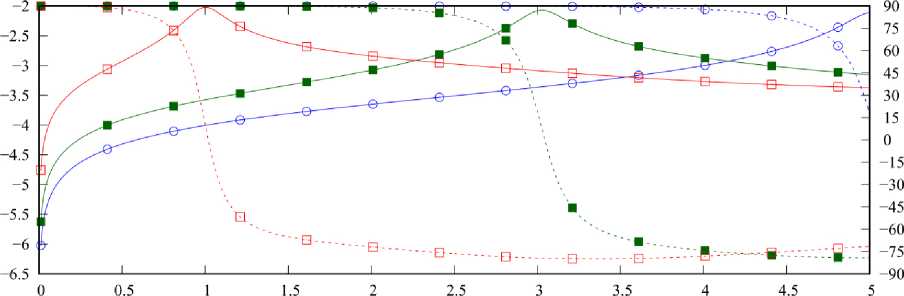
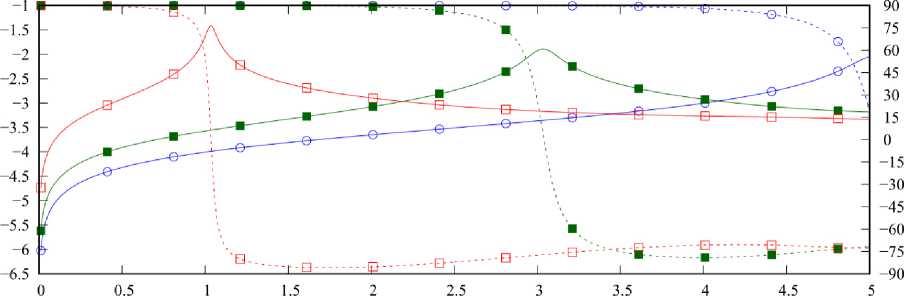
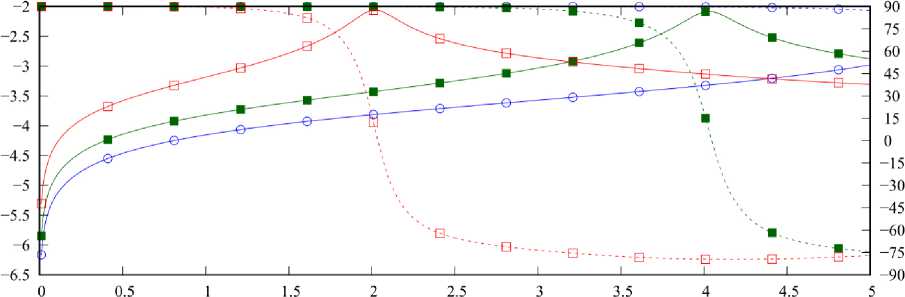
На рис. 7 приведены графики величин ν′ n ( x )=lg| ξ n ( x )|; ν′ n ′ ( x ) =arg ξ n ( x )
при κ =0,5. Представленные графики подтверждают резонансный характер поведения собственных чисел, при этом точки резонансов можно определить из условия ν′ n ′ ( x )=0. Резонансы СЧ в случае m = 1,4 наблюдаются в окрестности четных значений x , при этом для разных m одним и тем же резонансам соответствуют СВ, индексы которых отличаются на единицу. Отдельно следует отметить нерезонансный максимум ν 1 ′ в окрестности x =0 для m =1. Также здесь можно видеть, что добротность резонансов при m =1 немного выше, чем при m =4, вследствие того, что κ <1.
Важным моментом анализа оказался учет симметрии, так как в рассматриваемой структуре прослеживается эффект вырождения, заключающийся в совпадении резонансных точек для СЗ матриц различных СЛАУ. Этот эффект наблюда- ется для m = 2,3. При этом видно, что соответствующие резонансы при m =3 имеют большую добротность, так как κ <1.
В целом можно сделать вывод, что исследуемая структура в плане поведения собственных значений и формы собственных функций во многом схожа с рассмотренными ранее трубчатым вибратором [7; 8] и сферической спиральной частицей [6], вследствие чего предлагаемые ранее подходы, касающиеся построения аппроксимационной модели решения внутренней электродинамической задачи, в полной мере применимы и к рассматриваемой структуре.
Заключение
В статье рассмотрен вариант математической модели решения внутренней электродинамической задачи для эллиптической спиральной структуры, построенной с использованием тонкопроволочного приближения. Структура обладает двойной зеркальной симметрией, что позволяет сформировать математическую модель в виде че-
m =1
m =2
m =3
m =4
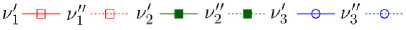
Рис. 7. Зависимости ν′ и ν′′ от x при различных значениях m ; κ =0,5
Fig. 7. Dependencies ν′ and ν′′ on x various values m ; κ =0,5
тырех независимых ИУ Фредгольма первого рода, записанных относительно соответствующих токовых функций, удовлетворяющих граничным условиям для электрической или магнитной стенки в точках пересечения образующей структуры с плоскостями симметрии. В рамках метода моментов полученные ИУ были сведены к СЛАУ относительно значений токовых функций на сегментах линеаризованной образующей. Решения СЛАУ сформулированы через собственные векторы и собственные значения матрицы СЛАУ. Собственные векторы СЛАУ аппроксимируют собственные функции интегрального оператора соответствующего ИУ. Для каждого ИУ проведен анализ поведения собственных функций и собственных значений интегрального оператора в зависимости от электрической длины образующей структуры и коэффициента эллиптичности при фиксированном электрически малом радиусе проводника.
Дана оценка невязки между собственными функциями, вычисленными при различных значениях указанных параметров. Показано, что невязка увеличивается с ростом электрической длины образующей структуры и с уменьшением коэффициента эллиптичности, но при выбранном шаге изменения параметров имеет довольно малые значения. Более детальный анализ позволил сделать вывод, что наиболее существенный вклад в значение невязки вносят собственные функции низших типов. Эти сведения формируют первичный ориентир при построении аппроксимационной модели решения внутренней задачи для рассматриваемой структуры.
Анализ форм собственных функций показал их близость к тригонометрическим функциям. Таким образом, они могут быть аппроксимированы соответствующими рядами, обладающими в данном случае быстрой сходимостью. В предельном случае при вырождении эллипса в окружность каждая собственная функция может быть аналитически точно определена парой тригонометрических функций.
Анализ зависимостей собственных значений от электрической длины образующей подтвердил их резонансный характер. В результате рассмотренная структура с этой точки зрения во многом аналогична рассмотренным авторами ранее электрическому вибратору и сферической спиральной частице. То есть можно утверждать, что существенный вклад в решение внутренней задачи вносит довольно ограниченный набор собственных функций. Также здесь стоит отметить, что учет симметрии структуры существенно упрощает проведение численного анализа при возникновении эффекта вырождения, когда одному собственному значению может соответствовать более одной собственной функции, что наблюдается в данном случае при значениях коэффициента эллиптичности, стремящихся к единице. При меньших значениях коэффициента эллиптичности наблюдается только эффект вырождения резонансных частот.
По мнению авторов, представленные в статье результаты имеют как теоретическое, так и прикладное значение. Теоретическое значение связано с развитием методов электродинамического анализа рамочных излучающих и переизлучающих структур. Предложенный подход дает углубленное понимание поведения рассматриваемых структур с точки зрения электродинамики и существенно упрощает интерпретацию получаемых численных результатов по сравнению со случаем непосредственного решения интегральных уравнений и их систем. Прикладное значение связано с тем, что представленные результаты могут послужить хорошим ориентиром при построении аппроксимационных моделей решения внутренней задачи для рассматриваемой структуры, а также для структур со схожей геометрией.
Список литературы Спектральные характеристики интегрального оператора внутренней задачи электродинамики для эллиптической рамочной структуры
- Wang T., Bell T. VLF/ELF input impedance of an arbitrarily oriented loop antenna in a cold collisionless multicomponent magnetoplasma // IEEE Transactions on Antennas and Propagation. 1972. Vol. 20, no. 3. P. 394–398. DOI: https://doi.org/10.1109/TAP.1972.1140212
- Ohnuki S., Sawaya K., Adachi S. Impedance of a large circular loop antenna in a magnetoplasma // IEEE Transactions on Antennas and Propagation. 1986. Vol. 34, no. 8. P. 1024–1029. DOI: https://doi.org/10.1109/TAP.1986.1143927
- Андронов А.А., Чугунов Ю.В. Квазистационарные электрические поля источников в разреженной плазме // УФН. 1975. Т. 116, № 5. С. 79–113. DOI: https://doi.org/10.3367/UFNr.0116.197505c.0079
- Мареев Е.А., Чугунов Ю.В. Антенны в плазме. Нижний Новгород: ИПД АН СССР, 1991. 231 с.
- Неганов В.А., Табаков Д.П., Задача о распределении поверхностной плотности тока по кольцевой полосковой антенне // Физика волновых процессов и радиотехнические системы. 2007. Т. 10, № 4. С. 8–19.
- Табаков Д.П. Об описании излучения и дифракции электромагнитных волн методом собственных функций // Известия вузов. Радиофизика. 2021. Т. 64, № 3. С. 179–191. URL: https://radiophysics.unn.ru/issues/2021/3/179
- Табаков Д.П., Майоров А.Г. О собственных значениях интегрального оператора сингулярного интегрального уравнения тонкого трубчатого вибратора // Физика волновых процессов и радиотехнические системы. 2019. Т. 22, № 1. С. 26–31. DOI: https://doi.org/10.18469/1810-3189.2019.22.1.26-31
- Табаков Д.П., Майоров А.Г. Аппроксимация решения внутренней электродинамической задачи для тонкого трубчатого вибратора методом собственных функций // Труды учебных заведений связи. 2019. Т. 5, № 4. С. 36–42. URL: https://elibrary.ru/item.asp?id=41664174
- Garbacz R.J. Modal expansions for resonance scattering phenomena // Proceedings of the IEEE. 1965. Vol. 53, no. 8. P. 856–864. DOI: https://doi.org/10.1109/PROC.1965.4064
- Harrington R., Mautz J. Theory of characteristic modes for conducting bodies // IEEE Transactions on Antennas and Propagation. 1971. Vol. 19, no. 5. P. 622–628. DOI: https://doi.org/10.1109/TAP.1971.1139999
- Harrington R., Mautz J. Computation of characteristic modes for conducting bodies // IEEE Transactions on Antennas and Propagation. 1971. Vol. 19, no. 5. P. 629–639. DOI: https://doi.org/10.1109/TAP.1971.1139990
- Справочник по специальным функциям / под ред. М. Абрамовица, И. Стигана. М.: Наука; Физматлит, 1979. 832 с.
- Интегральное представление электромагнитного поля геометрически киральной структуры / В.А. Капитонов [и др.] // Физика волновых процессов и радиотехнические системы. 2012. Т. 15, № 4. С. 6–13.
- Табаков Д.П. Тонкопроволочная модель фрактального симметричного вибратора на основе салфетки Серпинского // Радиотехника. 2015. № 2. С. 16–22.
- Табаков Д.П., Морозов С.В., Клюев Д.С. Применение тонкопроволочного интегрального представления электромагнитного поля к решению задачи дифракции электромагнитных волн на проводящих телах // Физика волновых процессов и радиотехнические системы. 2022. Т. 25, № 2. С. 7–14. DOI: https://doi.org/10.18469/1810-3189.2022.25.2.7-14
- Голуб Дж., Ван Лоун Ч. Матричные вычисления / пер. с англ. М.: Мир, 1999. 548 с.
- Стрижков В.А. Математическое моделирование электродинамических процессов в сложных антенных системах // Математическое моделирование. 1989. Т. 1, № 8. С. 127–138. URL: https://www.mathnet.ru/rus/mm/v1/i8/p127
- Интерактивная система просмотра системных руководств (man-ов) // OpenNET. URL: https://www.opennet.ru/man.shtml?topic=zgeev&category=3&russian=4
- LAPACK // Википедия. URL: https://ru.wikipedia.org/wiki/LAPACK
- Ludick D.J., Jakobus U., Vogel M. A tracking algorithm for the eigenvectors calculated with characteristic mode analysis // The 8th European Conference on Antennas and Propagation (EuCAP 2014). 2014. P. 569-572. DOI: https://doi.org/10.1109/EuCAP.2014.6901820
- Kalaba R., Spingarn K., Tesfatsion L. Individual tracking of an eigenvalue and eigenvector of a parameterized matrix // Nonlinear Analysis: Theory, Methods & Applications. 1981. Vol. 5, no. 4. P. 337–340. DOI: https://doi.org/10.1016/0362-546X(81)90018-3


