Спектральные решения для СМО с законами распределений в виде вероятностных смесей

В исследовании систем G/G/1 важную роль играет метод спектрального решения интегрального уравнения Линдли. Наиболее доступно этот метод на конкретных примерах изложен в классике теории массового обслуживания [1].

Настоящая статья посвящена анализу СМО H2/HE2/1, образованные двумя потоками, описываемыми обычными и сдвинутыми вправо от нулевой точки функциями плотностей гиперэкспоненциального и гиперэрланговского законов распределений второго порядка.

В ранних работах авторов доступно показано, что в системах, образованных сдвинутыми законами распределений, при одинаковом коэффициенте загрузки по сравнению с обычными системами среднее время ожидания становится меньше. Это достигается за счет того, что коэффициенты вариации времен поступления cλ и обслуживания cμ для сдвинутых законов распределений становятся меньше при вводе параметра сдвига t0 > 0. Таким образом, операция сдвига закона распределения трансформирует обычные марковские системы массового обслуживания в немарковскую систему G/G/1.

Результаты работ [2–4] в области СМО со сдвинутыми распределениями совместно с [1] позволили развить метод спектрального разложения решения интегрального уравнения Линдли и на рассматриваемые системы H2/HE2/1.

В теории массового обслуживания исследования систем G/G/1 актуальны в связи с тем, что они активно используются в современной теории телетрафика, к тому же нельзя получить решения для таких систем в конечном виде для общего случая. Метод спектрального разложения решения интегрального уравнения Линдли в исследовании систем G/G/1 играет важную роль, и большинство результатов в теории массового обслуживания по-

[@^Н © Тарасов В.Н., Бахарева Н.Ф., 2025

лучены именно с помощью данного метода. Одна из форм интегрального уравнения Линдли выглядит так [1]:

a ( t ) = p X e ^X 1 ¹ + ( 1 - p ) ^ 2 e ^X 2 ¹ ,                        (1)

b ( t ) = 4 q ^ 2 te ^{2 ц} 1 ^{ + 4 ( 1 - q ) ц 2 te ^{2 ц} 2 ^{ .                   (2)

W (y ) =

y

J

-да

W ( y - u ) dC ( u ) ,

y >  0;

o, y < 0,

где W ( y ) - функция распределения вероятностей (ФРВ) времени ожидания требования в очереди; C(u ) = P(й <  u ) - ФРВ случайной величины й = x - t, где, в свою очередь, x - случайное время обслуживания требования; t - случайная величина – интервал времени между поступлениями требований.

При кратком изложении метода решения уравнения Линдли будем придерживаться подхода и символики автора [1]. Для этого через A* ( s ) и B * ( s ) обозначим преобразования Лапласа функций плотности распределения интервалов между поступлениями и времени обслуживания соответственно. Суть решения интегрального уравнения Линдли методом спектрального разложения состоит в нахождении для выражения A *( - s) ■ B *( s) - 1 представления в виде произведения двух множителей, которое давало бы рациональную функцию от s . Следовательно, для нахождения закона распределения времени ожидания необходимо следующее спектральное разложение:

A * ( - s ) ■ B * ( s ) - 1 = у₊ ( s ) / у - ( s ) , где у₊ ( s) и у - ( s) - некоторые рациональные функции от s , которые можно разложить на множители. Функции у₊ ( s ) и у - ( s ) должны удовлетворять специальным условиям согласно [1].

Законы распределения (1) и (2) являются наиболее общими распределениями неотрицательных непрерывных случайных величин, поскольку обеспечивают широкий диапазон изменения коэффициента вариации.

Преобразования Лапласа функций (1) и (2) имеет

вид

A * (s ) = p

B ( ^s ) = q

^X 1 s + X j

+

( 1 - p )

^X 2 ^{s + X} 2

Тогда спектральное разложение для системы H2/HE2/1 преобразуется как

" ■ ^s )_ r p

x

V - ^{( s} )

^X 1

^ 1 - s

( 1 - p )

^X 2

^X 2 ^{- s}

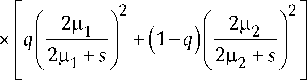
Первый сомножитель в правой части в квадратных скобках равен

^X 1 ^ 1 - s

( 1 - p )

^X 2

^X 2 ^{- s}

^X 1 ^X 2 ^-[ ^{p X} 1 ⁺ ( 1 ^{- p} ) ^X 2 ] ^s =     a 0 - a 1 s

^(X 1 ^{- s )(X} 2 ^{- s} )         ^(X 1 ^{- s )(X} 2 ^{- s} )

где промежуточные параметры a0 =^1^2, a 1 = = pX1 + (1 - p)^2. Аналогично представим второй сомножитель

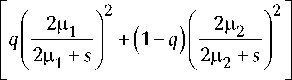
(     2 2       2          2 2

16 ^ 1 ^ 2 + 16 ^ 1 ^ 2 s + 4 ^ 1 s )

( 2 ^ 1 + s ) 2 ( 2 ^ 2 + s ) 2

( 1 - q ) ( 16 ц ² ц 2 + 16 ^ 1 ^ 2 s + 4 ^ 2 s ²)

+--2-----------2-------- =

( 2 ^ 1 + s ) ( 2 ^ 2 + s )

b 0 + b 1 s + b 2 s ²

( 2 ^ 1 + s ) 2 ( 2 ^ 2 + s ) 2

где промежуточные параметры b 0 = 16ц2ц2, b1 = = 16^1^2 [ q^1 + (1 - q )^2 ], b2 = 4[ q ^2 + (1 - q )^2 ]. Тог- да искомое выражение для спектрального разло- жения запишется как

У +( s )

^V — ⁽ s )

( a о - a i s ) ( b о + b i s + b 2 s ² )

( — 1 — s )( - 2 — s )( 2 ^ i + s ) ( 2 ^ 2 + s )

-

( - 1 — s )( - ₂ — s )( 2 ц 1 + s ) 2 ( 2 ц 2 + s ) 2

( — 1 — s )( - 2 — s )( 2 Ц 1 + s ) ( 2 ^ 2 + s )

Многочлен в числителе в правой части разложения (3), как правило, всегда имеет один нуль s = 0 [1]. В данном случае свободный член разложения также равен 0: a о b о — ^Х^ДД = 0

В числителе дроби в правой части разложения получили многочлен шестой степени — s ( s ⁵ — c 4 s ⁴ — c з s ³ — c 2 s ² — c 1 s — c о ), коэффициенты которого равны:

c о = a о b 1 — a 1 b о + Ь о ( - 1 + — 2 ) —                          (4)

• — 16 a _о ц 1 ц ₂ ( ц 1 +ц ₂),

c 1 = a о b 2 — a 1 b 1 — b о — 4 a о ( ^ 1 + ^ 2 ) +

+ 16(^1 + X2 )(^1 + Ц2 )^1^2 —16 a оН^2, c 2 = 4(^1 + —2 )[(^1 + ^2) + 2^1^2 ] —

• — 4( ^ 1 + Ц 2 )( a о + 4 ^ 1 ^ 2 ) — a 1 b 2 ,

c 3 = 4(-1 + -2 )(ц1 + Ц2) — 4[(ц1 + Ц2 )2 + 2ц1ц2 ] — a о, c 4 = -1 + -2 — 4(^1 + ^2)-

Коэффициенты (4) получены с помощью символьных операций Mathcad, поскольку числитель разложения (3) даже после введения промежуточных параметров содержит 42 слагаемых. Видимо и отсутствие результатов по рассматриваемой системе объясняется большой трудоемкостью выкладок.

Выделим многочлен в числителе разложения (3): s — c 4 s — c 3 s — c 2 s — c 1 s — c о ,                         (5)

• т. к. определение его корней составляет основную часть метода спектрального разложения.

Исследование многочлена (5) с коэффициентами (4) с использованием формул Виета подтверждает наличие четырех отрицательных действительных корней и одного положительного корня, либо вместо первых – двух отрицательных действительных корней и двух комплексно сопряженных корней с отрицательными вещественными частями. Исследование знака младшего коэффициента многочлена (5) показывает, что c о >  о всегда в случае стабильной системы, когда о <р< 1. С учетом знака минус в многочлене перед коэффициентом c о , формулы Виета не противоречат факту наличия четырех отрицательных корней у многочлена (5).

Обозначив отрицательные корни многочлена (5) либо их отрицательные вещественные части для удобства через — s 1 , — s 2 , — s 3 , — s 4 , а положительный корень через s ₅, отношение у + ( s )/ V ( s ) окончательно можно разложить на следующие множители:

• V + ( ^s ) = — s ( s + s 1 )( s + s ₂)( s + s 3 )( s + s ₄)( s — s ₅)          (6)

• ^V _— ( ^s )    ( ^ 1 — s ) ( — 2 — s ) (2 ^ 1 + s )² (2 ^ 2 + s )²

С учетом специальных условий [1] за функцию y+ (s)примем

s ( s + s )( s + s )( s + s ₃)( s + s )

V + ( s ) =------¹------ 2------ ³ ₂ ⁴ ,

(2 ^ 1 + s ) (2 ^ 2 + s )

т. к. нули многочлена (5): s = о, — s 1 , — s 2 , — s 3 , — s 4 , и двукратные полюсы s = — 2 Ц 1 , s = — 2 ^ 2 лежат в области Re( s ) <  о, а за функцию у_— ( s ) -

V — ( ^s ) = ^—

Р-1 s )P- 2 s )

^{( s — s} 5 )       ’

т. к. ее нули и полюс лежат в области Re ( s ) <  D .

Далее по методике спектрального разложения определим постоянную

K = lim *+H = ^s 1 s 2 ^s 3 ^s 4 .

s ^{> о} s      16 ^ 2 ^ 2

Постоянная K определяет вероятность того, что поступающее в систему требование застает ее свободной. Через функцию y + ( s ) и постоянную K определим преобразование Лапласа ФРВ времени ожидания W ( y ):

^ф + ^{( s} ) =

K

V + ( ^s )

s 1 s 2 s 3 s 4 ( s + 2 ^ 1 ) ² ( s + 2 ^ 2 ) ²

16 s Ц 2 Ц 2 ( s + s 1 )( s + s 2 )( s + s 3 )( s + s 4 )

Тогда преобразованием Лапласа для функции плотности времени ожидания будет функция s -Ф + ( s ), т. е.

W * ( s ) =

s 1 s 2 s 3 s 4 ( s + 2 ^ 1 ) ² ( s + 2 ^ 2 ) ² 16 Ц 2 Ц 2 ( s + s 1 )( s + s 2 )( s + s 3 )( s + s 4 )

Искомое среднее время ожидания в очереди равно значению производной от преобразования Лапласа (9) функции плотности со знаком минус в точке s = о:

dW * ( s ) ds

s = о

W = — + — + — + —

—

.

^s 1 ^s 2 ^s 3 ^s 4 ^H 1 ^н 2

Из выражения (7) при необходимости также можно определить моменты высших порядков для времени ожидания. Вторая производная от преобразования (7) в точке s = 0 дает второй начальный момент времени ожидания, что позволяет определить дисперсию времени ожидания. Учитывая определение джиттера в телекоммуникациях как разброс времени ожидания вокруг его среднего значения [7], тем самым получим возможность определения джиттера через дисперсию. Это является важным результатом для анализа трафика, чувствительного к задержкам.

Теперь перейдем к исследованию системы H₂/ HE₂/1 со сдвинутыми входными распределениями, т. е. к системе с запаздыванием во времени. Такую систему, в отличие от обычной системы, обозначим H 2 / HE 2 /1. Для этого введем в рассмотрение функции плотности распределения интервалов входного потока и времени обслуживания:

тральные разложения решения интегрального уравнения Линдли для двух рассматриваемых систем совпадают. Утверждение доказано.

Следствие. Расчетное выражение для среднего времени ожидания для системы со сдвинутыми распределениями будет иметь точно такой же вид, как у системы с обычными распределениями, но с измененными параметрами вследствие проведения операции сдвига во времени [2–4].

Теперь определим числовые характеристики, а через них – неизвестные параметры распределений (9) и (10) методом моментов. Для этого запишем их преобразования Лапласа:

A *⁽ s ) = ^[ p/' 1 + ( 1^— p Ь^²-^] e t ^{0 s} , ' 1 + s         ' 2 + s

* , в в (S) = [ q

I ] e ^— t ⁰ s .

Первая производная функции A* ( s ) со знаком минус в точке s = 0 дает значения среднего интервала поступления требований

a ( t ) = p ' 1 e ' ^{1 (} t t ⁰ ) + ( 1 — p ) ' ₂ e ' ^{2 (} t t ⁰ ) , b ( t ) = 4 q Ц 2 ( t — t 0 ) e 2 ^{H 1 (} t t ⁰ ) +

+ 4 ( 1 — q ) н 2 ( t — 1 ₀) e ^2Ц 2 ⁽ t t ⁰ ) .

Функции плотности (9) и (10) являются сдвинутыми вправо от нулевой точки на величину 1 0 >  0 гиперэкспоненциальным и гиперэрланговским распределениями второго порядка. Для нахождения среднего времени ожидания в очереди для этой системы докажем следующее утверждение.

Утверждение. Спектральные разложения A *( — s ) ■ ■ B *( s ) — 1 = v₊ ( s )/ V_— ( s ) для систем H 2 /HE 2 /1 и H₂/HE₂/1 полностью совпадают и имеют вид (6).

Доказательство. Для системы H 2 /HE 2 /1 спектральное разложение будет иметь вид

z+Ы.    '

V—(s) ?'г

^^^B

-+ ( 1 — p )? ^s         ' 2

—

X [ q

-] e t ^{0 s} x

s

- I ] e ^— t ^{0 s} — 1 =

^Т Л = p ^Л 11 ^{+ (1 —} p ^{) Л} 21 ⁺ t 0 ’

а вторая производная дает второй начальный момент этого интервала

2_.2       p J^{1 —} p )      p J^{1 —} p )

^тл = t 0 ^{+ 2} t 0 b"⁺-;    ^{] + 2} Нт⁺ г^] .

' 1     ' 2        ' 2     ' 2

Тогда квадрат коэффициента вариации вала поступлений будет равен

c 2 = Л

[(1 — p ² ) ' ² — 2 ' 1 ' 2 p (1 — q ) + p (2 — p ) ' 2 ]

[ 1 ₀ ' 1 ' ₂ + (1 — p ) ' 1 + p ' ₂ ] ²

.

интер-

Поступив аналогично с распределением (10), определим соответствующие характеристики для времени обслуживания.

^т ц = q н¹ + (1 — q ) н ₂ 1 + 1 ₀,

^Т ц = t 0 + ² t 0^[ ^ +

H

^{(1 — q} ) ] 3 [ ^{q (1 — q} ) ] Ц₂      2 LI²     LI^{2  L}

2 н   ^ 2

c

2 = ц ^{2 — 2} q ^ 2 ⁽ h ^—^ 2 ) ⁺ q ^{(1 — 2} q ⁾⁽ н^—н 2 ^{) 2}

' H

2[ 1 ₀ ц 1 ц ₂ + (1 — q ) ц 1 + q ц ₂ ]

.

'

= ^[ p V

—

'■

-+ (1 ^— p V ^s         ' 2

—

] X s

Механизм определения параметров

распреде-

x [ q

У экспонент показатели степени с противоположными знаками обнуляются, и операция сдвига тем самым нивелируется. Таким образом, спек-

лений (1), (2), (9) и (10) как с использованием двух первых начальных моментов, так и с использованием трех начальных моментов подробно изложен в [3] и [4] соответственно. Здесь же приведем готовые выражения для этих параметров. Для распределения (9) неизвестные параметры находим по выражениям:

Таблица 1. Результаты экспериментов для системы H₂/HE₂/1

Table 1. Experimental results for the H₂/HE₂/1 system

Входные параметры Input parameters		Среднее время ожидания Average waiting time
ρ	( c 2 , c ц )	СМО QS Н2/НE2/1	СМО QS H2/H2/1
0,1	(1; 0,71)	0,086	–
	(1;1)	0,111	0,111
	(2;2)	0,446	0,445
	(4;4)	1,791	1,779
	(8;8)	7,173	7,112
0,5	(1; 0,71)	0,755	–
	(1;1)	1,000	1,000
	(2;2)	4,043	4,044
	(4;4)	16,235	16,129
	(8;8)	64,844	64,178
0,9	(1; 0,71)	6,771	–
	(1;1)	9,075	9,000
	(2;2)	36,169	36,200
	(4;4)	144,773	144,833
	(8;8)	577,875	577,861

Таблица 2. Результаты экспериментов для системы H₂ / HE 2 /1

Table 2. Experimental results for the H - /HE - /1 system

Входные параметры Input parameters		Среднее время ожидания Average waiting time
( c X , c ц )	( c x ; c ц )	СМО QS H2 / HE -- /1			СМО QS H2/HE2/1
		t 0 = 0,99	t 0 = 0,5	t 0 = 0,01
0,1	(1;0,71)	0,03	0,04	0,09	0,09
	(1;1)	0,06	0,07	0,11	0,11
	(2;2)	0,23	0,36	0,44	0,45
	(4;4)	0,93	1,56	1,79	1,79
	(8;8)	3,74	6,38	7,16	7,17
0,5	(1;0,71)	0,26	0,48	0,75	0,76
	(1;1)	0,51	0,75	0,99	1,00
	(2;2)	2,04	3,15	4,03	4,04
	(4;4)	8,15	12,73	16,17	16,24
	(8;8)	32,62	51,07	64,58	64,84
0,9	(1;0,71)	2,49	6,00	6,77	6,77
	(1;1)	4,73	8,29	9,06	9,08
	(2;2)	18,92	33,20	36,14	36,17
	(4;4)	75,69	123,39	144,63	144,77
	(8;8)	302,78	528,43	577,29	577,88