Спектральные свойства магнито-фотонных кристаллов в области магнитного резонанса

дефектных модах, собственные частоты которых лежат в узких частотных интервалах дефектных минизон [11-13]. С помощью формирования различных типов дефектов и их расположения в структуре возможно эффективное управление оптическими свойствами ФК структур. К важному типу дефекта периодической структуры необходимо отнести инверсию, которая в простейшем случае заключается в изменении порядка следования слоев в одной из двух частей структуры при сохранении полного числа периодов, при этом получается магнитный или диэлектрический дефект.

Резонансный отклик магнитного дефекта на высокочастотное поле распространяющейся волны в области магнитного резонанса может существенно модифицировать спектральную линию дефектной моды вплоть до полного ее подавления. В этой связи в настоящей работе исследуется модификация спектров отражения бездефектной магнито-диэлектрической ФК структуры и структуры с дефектом инверсии во внешнем магнитном поле в области магнитного резонанса, а также возможность подавления осцилляционного режима и дефектной моды в рассматриваемых спектрах.

• 2.    МАТЕРИАЛЬНЫЕ ПАРАМЕТРЫ СЛОЕВ

В дальнейшем будут рассматриваться два типа одномерных магнитоактивных ФК структур. Первым типом является конечная бездефектная слоисто-периодическая структура, состоящая из чередующихся слоев магнетика и диэлектрика. Второй тип структуры представляет собой структуру с магнитным или диэлектрическим дефектом инверсии.

В состав структур обоих типов входят слои немагнитного диэлектрика, которые будем характеризовать толщиной Ld и скалярными диэлек- трической и магнитной проницаемостями (ДП и МП) Ed и ^d . Слои однородно намагниченного магнетика характеризуются толщиной Lm , в высокочастотном диапазоне описываются скалярной ДП Em и тензорной МП. Пусть внешнее магнитное поле H0 ориентировано вдоль оси ОХ, которая лежит в плоскости слоев. В этом случае отличные от нуля компоненты тензора МП Mm имеют вид: Mxx Mo = 1 и

„    to (to + iato)

M yy = M zz = M = ¹ + - -        ,

toH + iaco) - to

to _M to       (1)

^M zy = ^M yz = i M a = ,      • x2 2 ,

(toH + iato) - to

где to _H = y H o , CO M = 4 ^y M o , M 0 — намагниченность насыщения, y - гиромагнитное отношение, a — параметр магнитного затухания [14].

Будем считать, что волны распространяются вдоль оси OY, которая является осью периодичности структуры. Решение уравнений Максвелла с учетом направления распространения и ориентации подмагничивающего поля приводит к двум собственным волнам структуры – ТЕ и ТМ. Управляемой внешним магнитным полем является только ТЕ волна c компонентами волнового поля (E ,, H , H ). Волна ТМ типа с компонента-xyz ми (H x , E y , E z ) практически не реагирует на изменения внешнего магнитного поля.

Решения волновых уравнений для каждой из компонент в j — ом слое могут быть представлены в виде cуперпозиции прямой и обратной волн: F a j ^{y )} = F ) exp ^ i^{( to -} k j y^ ⁺ F ¹ exp f i^{( to +} k j y^ , (2)

где k j

= k o -j

волновые числа в каждом

из слоев, k o = to / С , а c - скорость света в вакууме. Для диэлектрических слоев ^E j = ^E d , M j = M d . Для магнитных слоев E j = E m , M j = M o в случае ТМ волны; ТЕ волны описываются эффективной МП

M j = M l = M — a ^M

( to _a + iarnf - to to 2 - to + iato ( to_a + to _H )

, (3)

где введены частоты магнитного резонанса to r = V to H to_a и антирезонанса to a = to H + to - [14]. Частотная и полевая зависимости величины M l (to, H _o ) , во многом, определяют особенности взаимодействия волны ТЕ с магнитоактивной ФК структурой.

На рис. 1 приведены частотные зависимости действительной части эффективной проницаемости магнетика Д _± для значений поля H ₀ = (400, 600) Э (сплошные кривые 1, 2), а

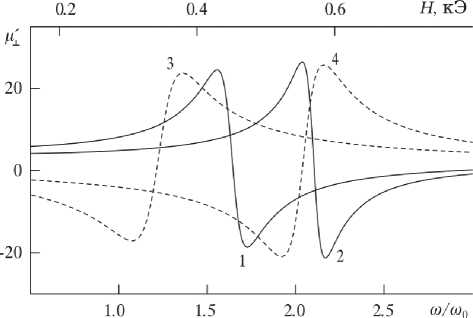
Рис. 1. Зависимости действительной части эффективной проницаемости магнетика от частоты для значений поля H ₀ = (400, 600) Э (сплошные кривые 1, 2), а также от величины подмагничивающего поля для значений частоты to = (1.5, 2.0) - 10 ¹⁰ c ^{- 1} (пунктирные кривые 3, 4); to ₀ = 10¹⁰ с^-1

также полевые зависимости для значений частоты to = (1.5, 2.0) -1О101 c 1 (пунктирные кривые 3, 4). Вычисления проводились для магнетика с параметрами 4лМ0 = 1780 Гс и АН = 15 Э. Видно, что каждому значению подмагничивающего поля отвечает свое значение резонансной частоты, а каждой частоте – резонансное значение магнитного поля. Увеличение поля приводит к сдвигу резонансной линии в область более высоких частот, а увеличение частоты – в область больших полей. Обратим внимание на область частот tor < to < toa, где действительная часть эффективной проницаемости Д± отрицательна (здесь введена частота антирезонанса to = to,, + to ). Указанные особенности фун-aHM кции позволяют за счет изменения магнитного поля обеспечить близость частоты магнитного резонанса или области отрицательности эффективной МП к центральной частоте фотонной запрещенной зоны или к частоте дефектной моды. Это, в свою очередь, должно приводить к существенной перестройке фотонного спектра магнитофотонного кристалла.

• 3.    ПЕРЕДАТОЧНЫЕ МАТРИЦЫ

И КОЭФФИЦИЕНТЫ ОТРАЖЕНИЯ И ПРОХОЖДЕНИЯ

Используя граничные условия для волновых полей, и условия периодичности, можно получить связь волновых полей в плоскостях, отстоящих друг от друга на произвольное число слоев. В случае бездефектной периодической структуры, содержащей конечное число периодов, эта связь осуществляется матрицей G = (M)n , которая является n -ой степенью матрицы одно- го периода. В свою очередь, передаточная матрица одного периода является произведением передаточных матриц слоев, составляющих период, т.е. M = N-N2 — N^Nf . При этом передаточные матрицы каждого из слоев имеют вид:

( C, -(kоM, / ikj) Sj ^

j I(ik, / kоm,)Sj Cj J, (4) где введены обозначения Cj=coskjLj, Sj=sin kjLj. С учетом (4) передаточная матрица одного периода имеет следующие матрич- ные элементы:

MU=CC - ^ ss2 , м2 = - ^ CS - k0M- SC, 11 1 2             1 2            12                1 21 2

M2k                 1кг м21 =-ik^^C2 +^CS2,   м22 = сс - ^ S-S2.

koM-      k0M2

Под инверсией понимается изменение порядка следования слоев одной части структуры по отношению к другой, при этом в середине структуры получаем либо магнитный, либо диэлектрический дефект. Инвертированному периоду Отвечает передаточная матрица M — N 2 - N 1 , матричные элементы которой связаны с элементами м _ˆ а трицы нормального периода соотношением M _ap — M _3-p _3-a , где a , p — 1,2 . Передаточные матрицы двух типов рассматриваемых структур можно представить в виде

A                  A

^A        . ^A Q , --- . Q         ^A        . --- Q . ^A . Q

G — ( M ) 8 ( M ) 8 и G — ( M ) 8 ( M )⁸ .

Энергетические коэффициенты отражения и прохождения для исследуемых ФК структур могут быть представлены следующим образом [13]:

R= f G 11 +G 12 - G 21 - G 22 J ² T= l G 1 ^+G12^+G21^+G22 J ,

( G 11 +G 12 +G 21 +G 22 )² ’(б)

где Gap - матричные элементы передаточной матрицы структуры. Указанные коэффициенты удовлетворяют закону сохранения энергии R+T+A=1, где коэффициент поглощения A определяет долю перешедшей в тепло энергии.

• 4.    БЕЗДЕФЕКТНАЯ ФК СТРУКТУРА МАГНЕТИК-ДИЭЛЕКТРИК

На основе приведенных соотношений проведен анализ спектров отражения и пропускания бездефектной периодической структуры, содержащей конечное число периодов, и исследована их модификация под влиянием внешнего магнитного поля. Передаточная матрица структуры, состоящей из n периодов, является n - ой степенью передаточной матрицы одного периода, т.е. (} — (3M )n — (NdNm )n. Для моделирования отражательных и селективных свойств ФК структуры используем следующие значения про-ницаемостей слоев: Ed =10 ’ Md 1 (материал МСТ10) и Em = 15.1, функция Mi (®, H0) используется та же, что и на рис. 1 (легированный иттриевый феррит-гранат 10СЧ6Б) [15].

На рис. 2 представлены спектры отражения бездефектной структуры ( N_dN_m ) ¹⁶ с толщинами слоев L _d =1.49 см и L m =1 .2 1 см. При этом оптическая толщина слоев диэлектрика

L — L, JEjl. = 4.71 см. Толщина слоев 0dddd магнетика выбрана таким образом, чтобы их оп тическая толщина L — L £ Lt — T/(->д

0m тщ\ mmmrn Od при значении Mm — - . На рис. 2а приведен спектр отражения ТМ волны, для которой в исследуемом диапазоне фактически отсутствует частотная дисперсия магнитной проницаемости M0 . Этот спектр отражения имеет все особенности, характерные для одномерной диэлектрической ФК структуры [3, 4]. На рис. 2б приведен частотный спектр отражения ТЕ волны, отвечающий значению H0 =300 Э. На характер этого спектра существенно влияет дисперсия эффективной МП Mi^ . По сравнению со спектром ТМ волны видна существенная его трансформация. В области, близкой к частоте магнитного резонанса, наблюдается подавление быстрых осцилляций коэффициента отражения. В широком диапазоне частот имеет место медленное изменение величины R со значением, близким к единице.

Дальнейшее уменьшение поля H ₀ ведет к смещению области резонанса в сторону более низких частот, что приводит к смещению области значительной перестройки спектра. Это видно из представленных на рис. 3 спектров отраже-

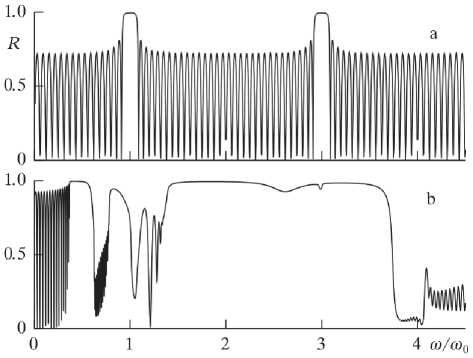
Рис. 2. Спектры отражения структуры ( M )¹⁶ с толщинами слоев L_d =1.49 см и L m =1 .2 1 см при M — 1 без приложения внешнего поля

(а) и H — 3 0 0 (b) ; to ₀ — 10 1 ⁰ с^-1

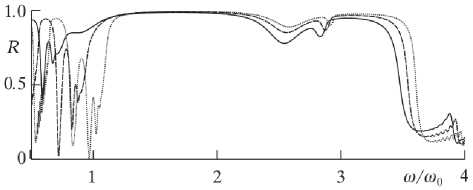
Рис. 3. Спектры отражения, полученные для значений поля H0 =100, 150, 200 Э (сплошная, пунктир, точки); to0 = 101 0 с-1 ния, полученных для значений поля H0 = 200, 150, 100 Э (кривые: точки, пунктир, сплошная).

На рис. 4 представлены спектры отражения для cущественно больших значений поля H 0 = ( 1,2,3 ) кЭ (a, b, с), для которых частота магнитного резонанса to r = ( 2.93 , 4.84 , 6.66 ) ■ 10 ¹⁰ c^-1 соответственно. В данном случае большая часть рассматриваемой частотной области относится к области прозрачности магнитного материалла, где поглощение близко к нулю. При H ₀ = 1 кЭ в спектре отражения четко выражены лишь первые две запрещенные зоны, центральная частота первой зоны равна to ₀₁ = 7.3 ■ 10 9 c^-1. Увеличение поля H ₀ приводит к уменьшению ширины запрещенных зон и смещению их в область более высоких частот. При этом в спектрах наблюдается образование более широких и четких четных запрещенных зон, что связано с неравен-

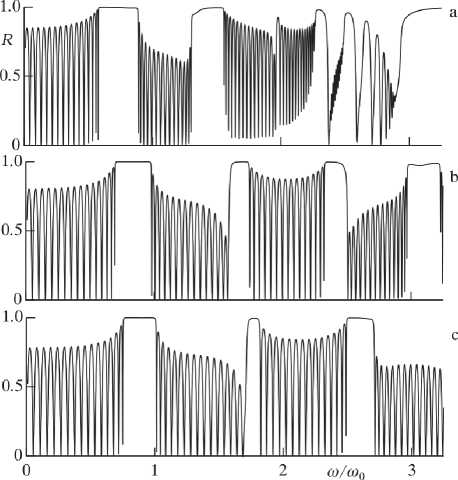
Рис. 4. Спектры отражения для больших значений подмагничивающегополя H0 = (1, 2,3)кЭ (a,b, с), для которых частота магнитного резонанса tor =(2.93,4.84,6.66)^1010c-1 соответственно; а= =1010с1

ством оптических толщин диэлектрических и магнитных слоев. При дальнейшем увеличении поля H 0 значение д _± в рассматриваемой частотной области приближается к единице и, в конечном счете, спектр преобразуется к виду, представленному на рис. 2a.

• 5.    ИНВЕРТИРОВАННАЯ СТРУКТУРА С МАГНИТНЫМ И ДИЭЛЕКТРИЧЕСКИМ ДЕФЕКТОМ

Рассмотрим теперь симметричную ФК структуру с дефектом инверсии. На рис. 5 приведены спектры отражения структуры ( M ) ⁸ ( M ) ⁸ для Д = 1 (a) и для эффективной магнитной проницаемости Ц ^ при H 0 = (2, 1,5, 1,) кЭ, (b, c, d). При увеличении магнитного поля магнитная проницаемость стремиться к единице и спектры приобретают вид как на рис. 5а, вторая и третья зоны исчезают и таким образом остаются 1 + 3 i зоны, где i ^ N . В случае магнитного дефекта инверсии в первой запрещенной зоне дефектная мода сдвинута к левому краю запрещенной зоны, а во второй зоне – к правому краю и т.д. При из-

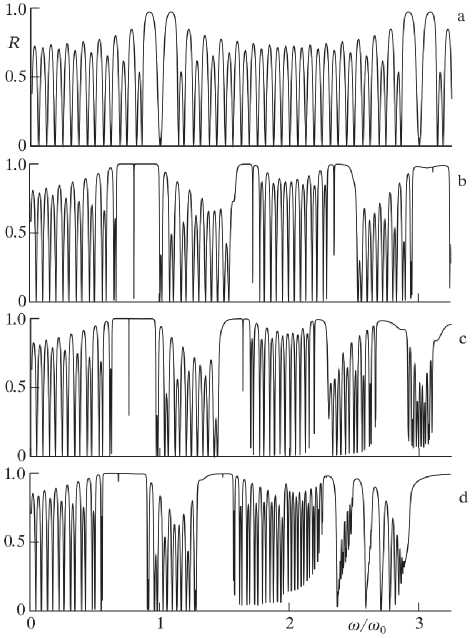
Рис. 5. Спектры отражения структуры

^{( N}d^Nm ^{)8( N}m^Nd ⁾⁸ при Д = ^{1 (a)}

и H ₀ = (2, 1.5, 1,) кЭ (b, c, d)

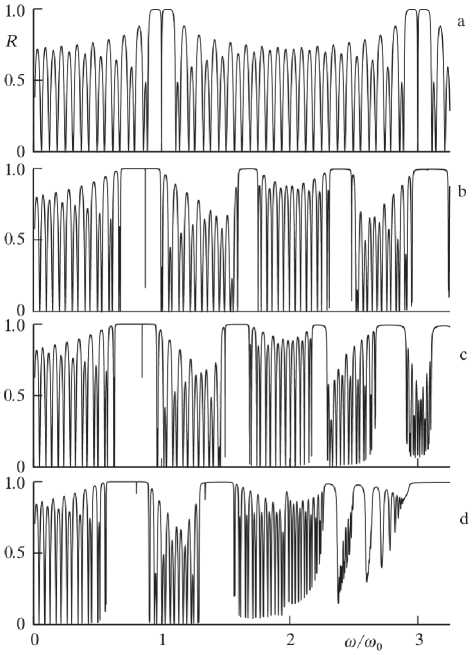
Рис. 6. Спектры отражения структуры ( N m N d ) ⁸ ( N d N m ) ⁸ при Д = 1 (a) и H ₀ = (2, 1.5, 1,) кЭ (b, c, d)

менении магнитного поля можно добиться совпадения частоты дефектной моды с частотой ферромагнитного резонанса, в этом случае происходит эффективное подавление дефектной моды. В случае диэлектрического дефекта инверсии в первой запрещенной зоне дефектная мода сдвинута к правому краю запрещенной зоны, во второй зоне - к левому краю. При д = 1 дефектная мода расположена в центре запрещенной зоны и для диэлектрического дефекта заметно уже, чем для магнитного дефекта. В случае магнитного дефекта инверсии в первой запрещенной зоне дефектная мода сдвинута к левому краю запрещенной зоны, а во второй зоне – к правому краю.

На рис. 6 приведены спектры отражения для структур (M)8 (M)8 для случая Д = 1 (а) и для эффективной магнитной проницаемости Д± при Hо = (2; 1,5; 1) кЭ, (b, c, d). В случае диэлектрического дефекта инверсии в первой запрещенной зоне дефектная мода сдвинута к правому краю запрещенной зоны, во второй зоне – к левому краю и т.д. При Д = 1 дефектная мода расположена в центре запрещенной зоны и для диэлект- рического дефекта заметно уже, чем для магнитного дефекта. В случае диэлектрического дефекта инверсии подавление дефектной моды менее полное, чем в предыдущем случае.

• 6.    ЗАКЛЮЧЕНИЕ

Проведенный в работе анализ указывает на возможность эффективного управления отражательной и пропускной способностью магнитоактивной ФК структуры в области магнитного резонанса с помощью внешнего магнитного поля. Для ТЕ волны продемонстрированно практически полное подавление осцилляций коэффициента отражения бездефектного ФК и дефектной моды в случае дефектной структуры при совпадении области магнитного резонанса с частотной областью фотонной запрещенной зоны. В случае распространения в исследуемых структурах ТМ волны резонанс в магнитных слоях отсутствует, поэтому управления ее волновыми характеристиками с помощью внешнего магнитного поля не происходит. Так, магниточувствительная дефектная мода в случае ТЕ поляризации становится немагниточувствительной в случае ТМ поляризации, т.е дефектная мода в указанной структуре является поляризационно-чувствительной. Выявленные эффекты могут быть положены в основу создания таких устройств управления излучением высокочастотного диапазона, как модуляторы, фильтры, переключатели.

Работа выполнена при поддержке Министерства образования и науки Российской Федерации в рамках федеральных целевых программ «Научные и научно-педагогические кадры инновационной России на 2009 - 2013 годы» и «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы»