Спектральный анализ интегродифференциальных уравнений с ядрами, зависящими от параметра

На полуоси R + = (0 , + то ) рассмотрим следующую задачу для интегродифференциаль-ного уравнения вида

4"7 +А2Н — [ К(t — s)A2rU,(s)d,8 = /(t), at           Jq t E R+,

n (+0) = <^q ,  n ⁽¹⁾ (+0) = y i .

Здесь A — самосопряженный положительный оператор, действующий в сепарабельном гильбертовом пространстве Н , имеющий компактный обратный, а параметр £ E (0 , 1). Скалярная функция К ( t ) допускает представление К ( t ) = ^І^ү C j e '■'*, где C j >  0, 7 j +i > 7 j >  0, j E N, 7 j ^ + to (j ^ + то ). Предполагается, что

∞

∞

b) ^2 C j <  + to .

j=i

a )

E - <  i , j = ⁷ j

Условие а ) означает, что ядро К ( t ) G L i (R + ) и ЦК ( t ) ^ L 1 <  1. В случае Ь) ядро К ( t ) будет принадлежать пространству Соболева: n₇(R . ), то есть будет обладать большей гладкостью.

Уравнение (1) является абстрактной формой уравнений, которые возникают во многих областях механики и физики, таких, как теория теплопроводности, в средах с памятью (уравнения Гуртина–Пипкина), теория вязкоупругости, теория усреднения. Модели распространения тепла в средах с памятью были изучены, в частности, в [9, 10]. Уравнения типа Гуртина–Пипкина возникают также в кинетической теории газов (подробнее см. [1], гл. 3), в динамике вязкоупругих твердых тел (см. [5], гл. 18) и в задачах управляемости термоупругих систем с памятью (см. [5], гл. 19).

Основная цель данной работы состоит в исследовании спектра оператор-функции, являющейся символом уравненя (1). Отметим, что в случае £ = 1 спектральный анализ уравнения (1) подробно проводился в работах [1, 2, 11, 12]. На основе результатов, полученных в [1, 2], в работе [13] установлено представление решений интегродифференцияльных уравнений в виде суммы рядов по экспонентам, отвечающих точкам спектра оператор-функций, являющихся символами указанных уравнений. Однако наличие параметра £ G (0 , 1) весьма существенно меняет структуру спектра оператор-функции. При этом появляется ряд новых эффектов по сравнению со случаем £ = 1 (подробнее см. п. 3). Здесь уместно подчеркнуть, что уравнение (1) изучалось многими авторами. Ограничимся здесь указанием работ [6—8], в которых рассматривался случай £ G [0 , 2 ]. Заметим, однако, что в известных нам работах при £ G (0 , 1) и, в частности, в работах [6—8] спектральный анализ символа уравнения (1) не проводился. Предлагаемая работа является естественным развитием результатов работ [1, 2, 11, 12].

• 2.    Корректная разрешимость

Пусть Н — сепарабельное гильбертово пространство, А — самосопряженный положительный оператор, действующий в пространстве Н , имеющий компактный обратный. Превратим область определения dom( A ³ ) оператора А^ ( ^ >  0) в гильбертово пространство Н р , введя на dom( A ^) норму || • Ц ^ = |А ³ • ||, эквивалентную норме графика оператора А ^р . Обозначим W ”₇(R + , А ”) – пространство Соболева вектор-функций, заданных на полуоси R ₊ = (0 , то ) со значениями в пространстве Н , снабженное нормой

IMIw^(R+RR = (^ exp^{( —} 2 7^ ( ^{|u (} ” ^{) ( t ) |} H + ^|A ” u ^{( t ) |} ^ ) dt^ , 7 >  0 .

Подробнее о пространствах W^(R + , А ”) см. монографию [15, гл. 1]. При п = 0 полагаем W ° ,₇(R ₊ , А ⁰ ) = L ₂ ,₇(R + , Н ), а при 7 = 0 будем писать W ” ₀ = W ” .

Определение 1. Вектор-функцию и назовем сильным решением задачи (1) и (2), если она принадлежит пространству W 2^ (R + ,A ² ) для некоторого 7 >  0 и удовлетворяет уравнению (1) почти всюду на полуоси R ₊ , а также начальному условию (2).

В работе [2] при £ = 1 была установлена корректная разрешимость задачи (1) и (2). Аналогичным образом для £ = (0 , 1) получаем следующий результат.

Теорема 1. Пусть для всех £ G [0 , 1] и при некотором 7 0 >  0 вектор-функция А ² - / ( t ) GL ₂ ,₇ о (R ₊ ,Н ) , а также / (0) = 0 , и условие ( а ) выполнено. Тогда

• 1)    eсли выполнено условие ( Ь ) и ^ о G Н 2 , ^ 1 G Н 1 , £ G [0 , 1] , то для любого 7 > 7 0 задача (1) — (2) однозначно разрешима в пространстве W^ (R + , А ² ) , и для ее решения оценка

"if 2 ( R ₊ ,A ² ) ^ ^d ( ^|А 2 ^ /|Ц₂ , ₇ ( R + ,Н ) ^{+ | А 2} ^ оҺ я ⁺ ||^А^1||н )                ⁽³⁾

справедлива с постоянной d , не зависящей от вектор-функции / и векторов 7 0 и ^ 1 ;

• 2)    если условие ( Ь ) не выполнено и у с € Н ₂.г , у 1 € Н |. г , € € (0 , 1] , то для 7 > 7 с задача (1) - (2) однозначно разрешима в пространстве W 2 7(R + , А ² ) , и для ее решения оценка

• 3.    Спектральный анализ

IMIwJy ( r ₊ ,a ² ) ^ ^d (Щ² ^ / ||²2^ ( r ₊ ,_h ) + ^А ^{2+? у} с ^ я + ^А ^{1+? у} 1||я)           (4)

справедлива с постоянной d , не зависящей от вектор-функции f и векторов у с и у 1 .

Доказательство сформулированной теоремы 1 приведено в [4].

Замечание 1. Случай € = 1 подробно изучался в [2], а также в гл. 3 монографии [1].

При € = 1 теорема 1 переходит в теорему 1 из работы [2].

Рассмотрим оператор-функцию цс) = с2i + а2— К(с)а2^, о<€< 1,

являющуюся символом уравнения (1), где К ( С ) = 52k =1 ( +77 является преобразованием Лапласа функции К ( t ), I — единичный оператор, действующий в пространстве Н . Обозначим через {е у } j =1 ортонормированный базис, составленный из собственных векторов оператора А , отвечающих собственным значениям а у: Ае у = а у е у , j € N. Собственные значения а у упорядочены по возрастанию: 0 < а і < 0 2 < • • • <  а _п • • • , при этом а _п ^ + то при я ^ + то . Во всех слeдующих утверждениях предполагается, что а _п ^ + то при я ^ + то .

Рассмотрим сужение оператор-функции L(C ) на одномерное подпространство, натянутое на вектор е _п:

¹ П ^(С) ^: = ⁽^^(С)^е п , ^е п ) = ^{С 2 + а} „ ^1 ^—

л^1- ) ^а п

∞

Е         = С ² + a » f n (<), 0 < € < 1.

^{с+ 7}Ч

Перейдем к вопросу о структуре спектра оператор-функции L(C ). В дальнейшем будем предполагать, что выполнено условие

sup {7 k < 7 fc +1 — 7 _k ) } = + то. k

Условие (6) было введено в работе [14], а также использовалось в работах [1], [2], [11], [12]. Описательно говоря, условие (6) означает, что элементы последовательности {7 k } k=i не могут приближаться друг к другу слишком быстро.

Теорема 2. Пусть выполнены условия Ь ) и (6). Тогда нули мероморфной функции 1 _п представляют собой счетную серию вещественных корней {^ и,к } ^=1 таких, что

—7 k < A n,k <  —7 к -1 , и lim Ц п,к = —7 k ,                        (7)

п ^^

а также пару комплекно-сопряженных корней р±, у+ = уп, представимых в виде д±(£)

д ± ( £ )

а ± ⁽ С ⁾

— 27^ ^Е ^ + о т<М ±<а п + °(7-^=))'

^а п у = 1          \^а п /      \         \^пп   / /

-

∞

2 а п Е = у ⁺ » у =1

(-)

V Оп/

± г (а п + о (1)) ,

2 7<Ь> Е =у + о(    ± г (ап + о(     ), ап      j=1          XU-TI /      \          \ап / /

€ € [0, 2),

€ = 1,

€ € (2, 1].

При выполнении условий теоремы 2 спектр я ( £ ) оператор-функции L(C ) совпадает с замыканием множества нулей {^ ± } ^ =1 и {ц _п,к } ^°k =1 функций 1 _п ( С ), т.е.

^{ст (} ^ ) = ( ^ n,k =1 ^ T,k ^ и ( ип°^ п ) •

о

Замечание 2. В соотношениях (8)–(10) подчиненные слагаемые, содержащие символы

(*)

выписаны отдельно для вещественной и мнимой частей /z ± ( £ ).

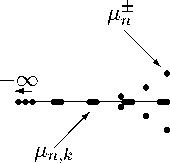
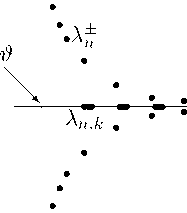
Замечание 3. При выполнении условий теоремы 2 и £ € (0 , 1) невещественные собственные значения р ± асимптотически стремятся к мнимой оси (см. рис. 1), поскольку Re М ± ( € ) ^ - 0 при а _п ^ то . В то время как в случае £ = 1 Re /z ± ( £ ) ^ — 2 ^J^ С (подробнее см. [2], а также [1, гл. 3]). При этом структура вещественного спектра u r при £ € (0 , 1) также отличается от случая £ = 1, поскольку при £ = 1 вещественные нули

Ц п,к ( £ ) ^ Х к , где Х к — вещественные нули функции ^2к =1 ^+у = 1 (подробнее см. [1,2]). Таким образом, при £ € (0 , 1) невещественный спектр оператор-функции L ( £ ) близок к спектру абстрактного волнового уравнения (при К ( t ) = 0).

- Im Л

І<С п

-га _п

Re Л

Рис. 1

Перейдем теперь к случаю, когда условие Ь) не выполнено.

Условие 1. Предположим, что последовательности {с к } к =1 , {7 к } к=1 имеют следующее представление:

А _

^Ск = "кА ^{+ О}

(к-7

7 к = вк + О(к ^{р- 1} ),к € N

при к ^ то , где константы А >  0 , В >  0, 0 < а <  1, а + 3 >  1 таковы, что ^2^ =1 | ^ <  1.

Замечание 4. Если 7 ^ +1 — 7 к ~ к ^ ^-р удовлетворяется при к ^ то с р >  1, то условие (6) выполнено при р < 23 .

Теорема 3. Предположим, что выполнено условие 1 и 3 >  2 . Тогда нули мероморфной функции 1 _п представляют собой счетное множество вещественных нулей {Л _п,к |к € N } :

7 к <  Л п,к <  • • • < —7 1 < Л п, 1 <  0 , и lim Л п,к = —7 к ,               (11)

п ^^

также пару комплекто-сопряженных нулей Л ± , Л ⁺ = Л - , представимых в виде

Г-1           ДОоДг-1\

^Л ± ( ^ ) = — Зг+-< ± і(с п + ^T-d + ^о                    , г € (0 , 2 ) , (12)

3Сп           х      3Сп      /       уС^

. +       АП1Вг-ү ,         AD2^r-1\   _ /   1 \

^{Лп (} £ ) = ^—    г +1-2 5 ± М° ^{п +} „ г +1-2 5 )^+О( 2(1- 5) ) ,                  ^{Т € [} 2 , 1) , ⁽¹³⁾

3СП          \     3Сп     /     \йп/

±,^     1А lnап

^Лп Ш = ^— 2 3 2(1- 5 ) ± ^{ІС п + О}( 2(1- 5 ) ) ,                                     ^т = 1 , ⁽¹⁴⁾

Сп                 \ Сп/ при ап ^ то, где г := ^+|—1, и константа D = D1 + iD2 определяется следующим образом:

D : =

і Г°

2 Л

dt 1 т

—т.---г = т того—г exp tT (i + t)    2 8іп(тг)

(3⁽¹ - ^{г )}) ■

При выполнении условий теоремы 3 спектр cr(L') оператор-функции L(C ) совпадает с замыканием множества нулей {А ± } ^1 и {Х п.к 0=1. функций 1п« ), т.е.

О) = (О =1О ) ^и   ' ^Л± ) -

Замечание 5. Случай £ = 1 подробно изучался в [2], а также в гл. 3 монографии [1]. При £ = 1 теорема 3 переходит в теорему 3 из работы [2].

• 4.    Доказательство основных результатов

Доказательство теоремы 2 . Доказательству теоремы 2 предпошлем доказательство следующей леммы.

Лемма 1. Рассмотрим функцию

«):= < ² + OS б — І^ ^Һ ^

\    а»      к=1 ^{С + Ак} /

=: С ² + a^N ( С ) ,

к = 1 .....N.      (16)

Тогда нули функции 1 _п n представляют собой множество действительных нулей {Ц п.к } N =i :

^А к <  ^ц п.к <  ^х п,к <   ^А к 1 <  ^ц п.к — 1 <  ^Х п,к — 1 < " " " <  ⁰ .

• ^ц п.к    ^х п,к — of ) . ^к — ^{1 - 2} . • • • ^N , ^a .  > ГО.

V а./ где т = 2(1 — £), если 0 < £ < |, т = 1, если ^ = 2, т = 2^, если | < £ < 1 и хп.к — действительные нули функции fп.N (С) вместе с парами комплексно-сопряженных нулей ц±, ц+ = ц—, асимптотически представимых в виде

ц ± ( € ) =	1 eN^ 2   2(W) а п	+ О ( « П (1 —« ) ± ' ( а П + О ( а П - 26 )) - 0 <  € < 2 -				(19)
ц ± ( € ) =	1 E N=1 С , - 2    а п	+ О	( а . )	± г (а . + О (1)) ,	« =2 -	(20)
ц ± ( € ) =	_ 1 eNo 2 Л1-9 а п	+ О	(а?)	± г(а п + О( ^1 -\        \ а.	)) -      <  1 -	(21)

Асимптотические формулы (19) – (21) были получены с помощью основной теоремы алгебры и теоремы Виета. Действительно, функция 1 _п,« имеет ровно N + 2 нулей, из которых N нулей (легко видеть графически) являются действительными и удовлетворяют неравенствам (17). По теореме Виета знаем, что

NL     /V^N.^\   NL   NL          NL

Һ ^..к =           — Һ А , ^- П ^.,к = ( — 1)^N П А , 1 — О)   -      (22)

к =1         \ ^а »      /   , =1      к =1               , =1   \     ^а.    )

N+2        N Е цп.к =—Ех, . к=1          ,=1 N+2                 «    /     с   \ Пцп.к = (—1)N+2аП Па, 1 — ^SN—6)  ,       (23) к=1                    ,=1   \    ап    ) где хп.к и цп.к являются нулями fn.N и I..N соотвестственно и Sn := Е«=1 ^• Из (18), (22) и (23) для т = 2(1 — ^), 1, 2^ получаем

N +2

Е ц .,к к=1

= Һ(...... . О ( а». ))

+ 2Re ^ ± ,

N +2 п ц »,к к=1

^N / = П( к =1 ⁴

Х п.к + О

I а.І)

ц + ц »

Здесь мы полагаем, что /z_ra,N +1 = Ц + и H n,N +2 = Ц ^- • Следовательно,

Re M ±

1 Е" 1 с ,

2 Л^{1- 5} ) ^а п

+ 0^ ,™ = 2(1 - 4), 1,²4

1т ц ± = а „ + О

(у

к = 1 - 2 4, 0, 2 4 - 1.

Таким образом, справедливы представления (19) – (21).

Асимптотические формулы (8) - (10) можно получить из (19) - (21) при N ^ то . Покажем теперь, что в круге В _е ( ц ⁺ ) = {С : |С — Ц + | <  е } функция £ _п (С ) имеет только один нуль для достаточно больших а _— Из сходимости ряда ^2^=1 С к вытекает, что для любого Е >  0, найдется N , для которого

∞

Е с . <  10 .

к N +1

Рассмотрим окружность ) _£( ц ⁺ ) = {С : С = Ц + + Ее^гф, 0 < ^ < 2тт} радиуса е и с центром в точке ц ⁺ (для корня ц — рассуждения совершенно аналогичны). Представим функцию 1 - (С ) в виде

‘ -N ( С ):= С ² + а - 6 — Лё Е ^

\   <    .=i ^{С + 7к}/

^ —, ^ ^(С ) ^: —

∞

-а- Е k=N +1

С к

^{С +} 7 к .

Выберем столь малое е >  0 так, чтобы в круге В _е( ц ⁺ ) не было других нулей функции l _—,N ( С ). Оценим функцию 1 _-,n ( С ) на окружности D _e(/z ⁺ ). С этой целью заметим, что для С € D _e (n + )

( /  . y^N

- 2

\    а-

2                            1

- Ц -,к + Е cos(< ^ )^ + ( а - + е sin( < )) ² j

— а - - е.

Для других случаев рассуждения аналогичны. Заметим, что при С € ) _£( ц ⁺ ) верны следующие: |С - Ц + | = Е , |С - Ц ^- | >  2 а _- - Е . На основании указанных неравенств получаем следующую оценку снизу:

N

П ^{( С} - ^Ц -,к ^{)( С - ц + )( С - Ц} -)          ^ ^{( а} - ^{- e ) N +} 1 ^Е .                ⁽²⁵⁾

^к =1                                   ( e d _e ( ^ + )

Из неравенств

^{|С + 7} 3 | C G D _E ( ^ + ) <

N

Z-^ к=1 Ск

2а»-^>

+ 7 j + Е cos( < )

+ |а - + е sin( < ) | <  М 1 + 2е + а - ,

г^{де М} 1 = f 2 2(1 - 4 ) ^ к =1 ^С к ) \ ^п                  /

+ 7 j , приходим к оценке

N

П ^{( С -} 7 к )         <  ^{( а} - ^{+ 2 е + M} 1 ^{) N} .

^к =1           ( E D _E (p+)

Теперь из (25) и (26) получаем

^|l -,N ^{( С} ) | =

¹ П к =1 ^{( С - ц} -,к^{)( С - ц + )( С - ц} - ) | | п N =1 ( c - 7 к) |

- ^Еа- 0^{- О}Ш у

С € D^Y

Таким образом, при достаточно большом а „ будет справедливо неравенство

I«„,n(С)1 > 2",      С 6 DMY(27)

Оценим теперь модуль функции т„^(С) сверху при достаточно больших а„: го      2f           ^     2f

I                     °„ Ck /        °„ Ск /   °„ е / е т”,”(<)|- 2X + 71|- ^., «„ - «- («„ - г) 10 <““5'     С ' D-°'”).

На основании неравенств (27) и (28) имеем

I1„,n(С)| > ^   -5 >|т)|, и согласно теореме Руше получаем, что в круге B£(/z+) функция 1„( С) имеет один простой нуль //+ (или //— соответственно) при достаточно больших а„.

Покажем теперь, что множество нулей функции

^ = 2 + /„(С) := д„(С) + /„(С) °„

совпадает с объединением счетной серии действительных нулей {ц „,к | к 6 N } и парами комплексно-сопряженных нулей // ± , // + = // - . Фиксируем п 6 N и рассмотрим прямоугольный контур Г = {С ⁺ U С - U С U С * } , где

С ± = {С 6 C : Re C = ±X , | 1т С | - Y, X, Y >  0 }, С * = {С 6 C : С 6 С },

С = {С 6 C : | Re C| - X, Im C = ±Y, X, Y >  0 }.

В [3] было приведено полное доказательство того, что на прямоугольном контуре Г справедливо следующее неравенство:

|/ „( С ) | < |д „( С ) |,     С 6 г.                                           (31)

Таким образом, согласно теореме Руше и принципу аргумента получаем

X(д„(С)) - р(д„(С)) = X(/„(С)+ д„(С)) - р(/„(С)+ д„(С)), где X и Р - соответственно число нулей и полюсов внутри контура Г, причем каждый полюс и нуль считаются с учетом их порядка и кратности соответственно. По определению функции д„(С), X(д„(С)) - Р(д„(С)) = 2. Внутри контура Г функция /„(С) + д„(С) имеет X полюсов: -7n, -7n —1,..., -71. Следовательно, X(/„(С) + д„(С)) = X + 2. Легко видеть (графически) (см. также [14]), что функция /„(С)+д„(С) имеет X +1 или X действительных нулей внутри контура Г, которые удовлетворяют неравенствам (7) в зависимости от того, ^n,„ < Xn или ^n,„ > Xn. Но если ^n,„ < Xn, то /„(С) + д„(С) имеет один комплексный нуль внутри контура Г, что невозможно, так как (/„ + д„)(С) = (/„ +д„)(С)• Следовательно, внутри контура Г существует ровно два комплексных нуля ^± , где ^+ = ^-.

Доказательство теоремы 3 . Как и в теореме 2, здесь мы рассмотрим ту же самую функцию (30) и покажем, что множество всех её нулей совпадает с объединением счетной серии действительных нулей {А „,^ |к 6 N } и с парами комплексно-сопряженных нулей А ± , А + = А - . Более того, покажем, что последовательности {А „,^ |к 6 N } удовлетворяют неравенствам (11). Во второй части доказательства мы покажем, что для комплексно-сопряженных нулей А ± справедливы асимптотические представления (12) - (14). Аналогично [2] можно доказать, что справедливо неравенство (31) для всех С 6 Г = {С ⁺ U С - U С U С * } (подробнее см. [3]). Остальные утверждения следуют из теоремы 2.

Основная идея доказательства теоремы 3 заключается в замене функции

ГО Cl,

К ( £ ) = ^2^=1 rj\, , апроксимирующей функцией, выраженной интегралом

Г ~    А h(^ ) = к ПС + Bt^)dt, с последующими оценками функции һ(С) в области {£ G C : | arg С| < т — 6,6 > 0}. Апроксимация функции К (() функцией һ(() была установлена в работе [2, лемма 3].

Покажем, что комплескные нули функции 1п(С) асимптотически представимы в виде Х± = ±гап + тпап, п G N при п ^ то, где тп - некоторая числовая последовательность. Для этого достаточно показать, что асимптотическое представление Х+ удовлетворяет уравнению ^(2—2 = ^\) + 1, которое равносильно уравнению К(Х+) = аП(1 6)тп(тп + 2г). Отсюда “П 1      “п получаем, что т =    К(х+)

а п^1—Ч т _п + 2г)

.

Обозначим һ _п (т ) : = в виде т _п = h _n (т _п ),

^(Аг.

2(1 _- П ---—, ^ п = га _п + та _п . Тогда уравнение (32) можно переписать

“ п      ( т +2 г )

откуда получаем, что число тп является неподвижной точкой отоб- рожения т ^ һп(т) при п ^ то. Следовательно, достаточно показать, что при п ^ то отоброжение т ^ һп(т) является сжимающим. Таким образом, искомое решение тп будет найдено как предел последовательности тП при к ^ то, где тП = һ(т^-1), тП = 0,тП = тп.

Докажем, что отображение т ^ һ _п (т ) является сжимающим. Это следует из леммы 2, которая была доказана в [2], и из оценки

Іһ П( т ) | =

К ( Х + ) — К ‘ (Х + )(а „ т + 2 га „) а П ^{1 - )} (т + 2 г ) ²

ІК ‘ (Х + )(2( _п ) | + 1К(Х + )1

2(1- 6 ) а п

|т। <  2 •

Лемма 2. На множестве {^ G C : | arg С | <  т — 6,6 >  0 } справедливы следующие соотношения: |^К ‘ ( С ) | ^ 0 и |К ( £ ) | ^ 0 при |С| ^ то .

^/»z.

Замечание 6. һп(тп) = — . 2(1-5) [1 + °(тп)], п ^ то при п ^ то. Действительно, ис-“п пользуя разложение в ряд Тейлора в тп = 0, непосредственно получаем

, , _х       г к (га„)_г,

һп(тп) = — 2 2(1-о [1 + o(т")], п ^ то- а„х

Таким образом, для т _п справедлива следующая асимптотическая формула:

^(а,, тп = — 9 КГ-ПТ [1 +О(т")], п ^то-                       (33)

² а П

Следующая лемма приведена в [2] и используется для того, чтобы получить формулы (12) - (14).

Лемма 3. Если | arg ^ | < т — 6,6 >  0 , то

,      АВ¹-¹ ^ dt

К(< )= .'ki' / t' (exp(ip)+ t) + ° (j<|) ’           если 0 <Г< 1'

- , Аln I в + 11       / 1 \

K<(C) = '—L + ° ( |^| ) ,                          если г = 1.

Используя лемму 3 и следующий результат:

D = 2 f0 t'^'+tn^sn^^^ — r)), агд(іа") = ?’ получаем следующую асимптотическую формулу для случая 0 < г < 1:

г К_  г АВ;   ^ at , О ( 1 ) _  ADB1- । О

2 ^А« ^{п )} =  2 Р1«пЗ Jo t ^r( г + t ) ⁺   <«пУ = Р« п ⁺

Здесь D : = D i + zD 2 . Таким образом:

iK(ianV          / ADBr-i    /1

ТП = — 2 22(1-$) [1 + О(Тп)] = ( — о ^+2(1-$) + О ( 1+2(1-$) ) Н + О(Тп)]‘ «п                   \ р«п            у«п/ /

Пусть R 1 + ^ 2 := ( - рР ■ } + ( -г jP — } . Тогда

Т п

R 1 + ^ 2

„ г+^ - б ) « п

R 1

_п г+2(1- $ ) « п

.       1 V Mi + ^R2 ,

^{+ О} (  1+2(1- $) ) ⁺ (   г +2(1- $ ) ^{+ О}

У « п        /    \Пп

^{+ О} (  1+2(1- $) ) ^{+ О} (  2 г +4(1- $) )

У « п       / у«п        /

( П^))^{О (}^ =

Д 2

⁺ г +2(1- $ ) ’

где R =

Д 1 + Й 2 г +2(1 - 5 )

“ п

+ ^О( T+^ht - i )) .В

“ п

случае 0 <  г <  1, справедлива следующая формула:

Т п

R 1 + R 2

г +2(1- $ ) « п

+О(

min{1+2(1- $ ) , 2 r +4(1- $ )} « п

) ■

Т п

R 1 + R 2 г +2(1- $ )

^{+ О} I 1+2(1-$) ) ’ У «п       /

0 < г <  2 ,

2 <  г <  1 .

Вновь используя лемму 3, в случае г = 1 имеем

|_/ < ( г« п) = - j ^A ln l iLiil ₊ О ⁽1) = - ^1А

2            2 p     г« _п         \«_п/      2 p « _п

+ о( Р-

V «п/

Таким образом, получаем асимптотическую формулу:

Т п

1 A   ln « _п

2 p _п¹ + ² ( ¹ - $ )

1 «п

^{+ О} (   1+2(1-$) ) .

У «п       /

Поскольку Х ± = ±г« _п + Т _п « _п, из асимптотических формул (36) — (38) вытекает, что

ReA±(^) = - В" 1AD\ +О| --------1),          0 <г< 1, пУ’ д г+2( 1 -$)       \ min{2(1-$),2r+4( 3-$)}/ ,                         2,

Р«п   2          \С1п               4/

ReX±(€) = -       г+2( 1 -$) + О f ^-у^ ,                  2 < г < 1, рв1 г «п   2         \ «п/

ReX±(€) = - 2 р ^(1-$)- + О f ^(1-$)^ ,                             г = 1.

«п

• 5.    Заключениe и комментарии

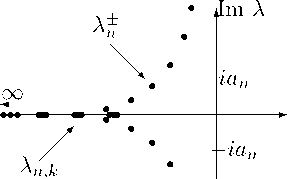
При выполнении условий теоремы 3 возможны следующие случаи.

1) При г = 1 и £ е (0,1), и при г е (0,1) и е е (0, ^+-1) U {2}, имеем Re А±(е) ^ -0, то есть

При

г е

При

г е

Re А r

Рис. 2

(0 , 1) и е е (^ , 1), Re А ± (^) ^

Re A ±

(е) =

AD 1

рв ¹

-

т

а,

2 ( 5

' п

r

r

r

-

∞

^A n,k

r

r

r

А ±

r

r

r

r

r

r

-

то , когда а _п ^ то , так как

^{1+1 )} + о(

Im А

га _п

-

Шп

Рис. 3

min { 2(1 — 5 ) , 2 т +3 — 4 5 } а п

Re А

(0 , 1) и е = ^ ±1 получаем следующую асимптотику:

Re A ± =

AD 1

рв ¹

—

т

+ О

( ^Y ап

)•

которая зависит только от г . Тогда Re А ± ( е ) ^ — ^^і-_г = ^ при а _п ^ то . Если A >  В , то рис. 4, а если A < В , то рис. 5.

-∞

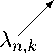
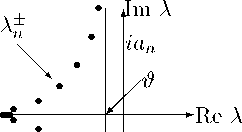
—шп

. ImА гап

-------*- Re А

^—І ^а п

Рис. 4

Рис. 5

Таким образом, случай е е (0 , 1) существенно отличается от случая е = 1, поскольку при е = 1 Re А ± ( е ) ^ —то (подробнее см. [2]). Тем самым наличие параметра е е (0 , 1) значительно усложняет структуру невещественного спектра оператор-функции L(p ). Так, в случаях 1) и 3) структура невещественного спектра близка к спектру волнового уравнения, а в случае 2) к спектру абстрактного параболического уравнения.

Автор выражает глубокую благодарность профессору В. В. Власову за постоянное внимание к работе и конструктивные замечания, а также участникам семинаров под руководством А. Л. Скубачесвкого и профессора А. А. Шкаликова за полезные обсуждения.

Работа выполнена при поддержке гранта Мексиканского центра экономических и социальных исследований (CEMEES в испанской аббревиатуре).