Спектральный метод и его применение при решении задач дифракции в закрытых волноводах

Дифракция электромагнитных волн на неоднородностях в волноводах является ключевой задачей при расчете функциональных узлов СВЧ-, КВЧ- и оптического диапазонов волн. Особое значение при этом имеют проблемы решения задач дифракции на переходах сложной формы (в том числе плавных) ввиду их широкого применения в качестве согласующих и возбуждающих устройств.

Среди методов решения дифракционных задач на неоднородностях в волноводах можно отметить метод частичных областей (МЧО) [1–3], метод поперечных сечений [4–7] и ряд универсальных сеточных методов [8–9]. Недостатком МЧО является необходимость проведения расчета полного спектра собственных волн для каждой из областей разбиения переходного участка, которых в случае ступенчатой аппроксимации плавных переходов может быть достаточно много и которые в общем случае могут описываться самостоятельными краевыми задачами. Метод поперечных сечений, как правило, эффективен при медленном изменении параметров волновода по продольной координате. Недостатками сеточных методов являются их повышенная потребность в вычислительных ресурсах и отсутствие физической наглядности.

Предлагается метод решения внутренних задач дифракции на участках волноводов с произвольным диэлектрическим заполнением, использующий спектральный метод.

1. Постановка задачи

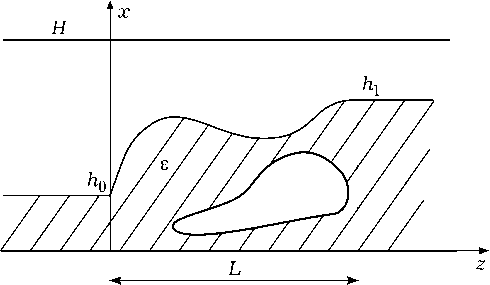
Рассмотрим задачу дифракции Н-волн на участке планарного волновода с произвольным диэлектрическим заполнением, соединяющим две продольно-регулярные планарные направляющие структуры (рис. 1).

Электромагнитное поле в левой регулярной области представляем суперпозицией падающей волны и полного набора отраженных Н-волн с амплитудными коэффициентами Г n ; поле в правой регулярной области – суперпозицией прошедших волн с амплитудными коэффициентами T_n .

В области перехода с произвольной функцией распределения диэлектрической проницаемости

б ( x , z ) электромагнитное поле должно ворять уравнениям Максвелла:

rot ( E ) = - i юц о Й ;

rot ( Й ) = i юб ( x , z ) Б о E .

Из системы (1) получаем уравнение rot rotE = к2Б (x, z) E, которое для случая Н-волн планарного да примет вид d2Ey d2Ey    9 , x

---+      + k 2 Б ( x , z ) E = 0.

d x ²     d z ²                y

Поле в области перехода будем искать J

^Ey = S f j ( ^z ) sin ( ^a j x )

j = 0

удовлет-

волново-

в виде

где a j = п ( j + 1 ) / Й , Н — поперечный размер планарного волновода.

S

Рис. 1. Произвольный переход между двумя регулярными планарными волноводами

( - N ^{( 0 )} + k 0 W ^{( 0 )} ) a + ( - N ^{( 0 )} + k 0 W ^{( 0 )} ) a = 0;

( - N ^{( 1 )} + k 2 W ^{( 1 )} ) a + ( - N ^{( 1 )} + k 2 W ^{( 1 )} ) a = 0

или

= 0,

'- N ^{( 0 )} + k 0 W ^{( 0 )} _v- N ^{( 1 )} + k 2 W ^{( 1 )}

- N ^{( 0 )} + k 2 W ^{( 0)>} - N ^{( 1 )} + k ^ W ^{( 1 )} ,

где

Допустимость представления поля в виде (4) показана в [4; 6].

Функции f j ( z ) , определяемые на отрезке z е [ 0, L ] , будем искать в виде

K fj (z) = ^ [aj,k sin (Ykz) + aj,k cos (7kz)] ,       (5)

k = 0

где Y k = ⁿ ( ^k + 1 ) / L ^{, Y} k =^{n k} / L .

Подставив (5) в (3), получим следующую формулировку:

JK

Ey = ^^[ aj, k sin (Ykz) + j=0 k=0

+ a j , k cos ( Y кz ) ] sin ( a j x ) ,

LH

Nq⁰ n = ( ^a n ⁺ Y n ) J J ^sin (^a n^x ) ^sin ( Y n z ) ^x

x sin ( a q x ) sin ( y q z ) dxdz ;

W^{( 0 )}

q , n

LH

J J s ( x , z ) sin ( a _nx ) sin ( y _nz ) x 00

x sin ( a q x ) sin ( y q z ) dxdz ;

LH

Nq0in = (an + Yn) J J sin (anx) cos (ynz) X x sin (aqx) sin (yqz) dxdz;

W^{( 0 )}

q , n

(9а)

которую, как показано в [4], можно представить в виде одной суммы:

LH

J J s ( x , z ) sin ( a _nx ) cos (y _nz ) x 00

x sin ( a q x ) sin ( y q z ) dxdz ;

N

E y = ^ ^{[ a}n sin (^a n x ) sin ( Y n z ) ⁺ n = 0

+ a n sin ( a n x ) cos ( y n z ) ],

N ^{( 1 )} q , n

LH

= (an + Yn) J J sin (anx)sin (Ynz) x

где N = ( J + 1 ) ( K + 1 ) - 1, а коэффициенты a _n , Y _n и Y n включают в себя все возможные сочетания коэффициентов из (4) и (5) [4; 6].

Подставляя (5) в (3), получаем следующее

x sin ( a q x ) cos ( y q z ) dxdz ;

W^{( 1 )}

q , n

LH

J J s ( x , z ) sin ( a _nx ) sin ( y _nz ) x 00

уравнение:

N

• - ^ ^an ( ^a n ⁺ Y n ) ^sin (^a n x ) ^sin ( Y n z ) ^- n = 0

N

• - ^ ^an ( a n ^+Y 2 ) sin ( a n x ) cos (^y n z ) + n = 0

N

• + k 2 s ( x , z ) ^ a n sin ( a n x ) sin ( y n z ) +

n = 0

x sin ( a q x ) cos ( y q z ) dxdz ;

N ^{( 1 )} q , n

LH

= (an + Yn ) J J sin (anx) cos (Ynz) x

x sin ( a q x ) cos ( y q z ) dxdz ;

W^{( 1 )}

q , n

LH

J J s ( x , z ) sin ( a _nx ) cos ( y n z ) x

(9б)

N

+ k 2 s ( x , z ) ^ a n sin ( a _nx ) cos ( y n z ) = 0.

n = 0

x sin ( a q x ) cos ( y q z ) dxdz .

Проецируем уравнение (7) на sin ( a q x ) sin ( y q z ) и на sin ( a q X ) cos ( y q z ) , в результате чего получаем

два матричных уравнения:

Видно, что матрица S из (9) имеет 2 N столбцов и 2 N - 2 J строк, т. е. не является квадратной. Для решения поставленной задачи необходимо добавить 2 J строк, которые получим из граничных условий.

Запишем условия непрерывности тангенциальных компонент поля на границах между выделенными областями:

M

E 0 + Е г m E m = E y ( x ,0 ) ;

^^^^^^в

H 0

m = 0

M

У г н(0) = m m m=0

- i d E y ( x ,0 ) ;

ЮЦ 0     d z

M

E y ( x, L ) = Е T m E m ;

m = 0

- i dE y ( x , L ) ЮЦ 0     d z

M

= у т н ^{( 1 )} / m m ^.

m = 0

( 0 )      ( 0 ) ( 1 )      ( 1 )

Здесь Em , Hm , Em , Hm – поля ортонормиро- ванных собственных волн левого и правого регулярных волноводов соответственно; Ey (x, 0) , Ey ( x, L ) - поле в области перехода на его границах, представляемые в виде (6).

Подставив (6) в (10), с учетом равенств cos ( Y n L ) = ( -1 ) n , cos ( у _nL ) = ( -1 ) n ^{+ 1} получаем систему функциональных уравнений:

MN

Eо + ЕгmEm^ = Е an sin (anx);

m=0

M-. N

H 0 ^- E ^г m^Hm = — an , n s Y n sin (^a n x ) ; ^(11б) m = о         ®^ o n = 0

NM

(12а)

I ( 0 )- Q ( 0 ) ■ Г = [ J ]   [ J X M ] [ M ]	R ( 0 ) ■ a ; [ J X N ] [ N ]	(12б)
Q ( 1 ) ■ a = t ; [ M X N ] [ N ]   [ M ]		(12в)
R ( 1 ) ■ a = Q ( 1 ) ■	T ,	(12г)
[ J X N ] [ N ]   [ J X M ]	[ M ]

где

К^{( 0 )} m , n

H

= J H mm sin ( a _nx ) dx ;

H

I j ^{0 )} = J sin ( a j x ) H 00 ) dx ;

H

Q jj0m = J sin ( a j x ) H mm) dx ;

_R ( 0 )

H

• —^n J sin ( a ^-x ) sin ( a _nx ) dx ;

^Юц о 0

H

Q m ) n = ( -1 ) ⁿ j H m sin (

a _nx ) dx ;

^- i У n (^{- 1} )

ЮЦ о

H

n + 1 H

----J sin ( a j x ) sin ( a _nx ) dx ;

Q jm = J sin ( a j x ) H m dx .

Нетрудно видеть: несмотря на то, что система (12) состоит из четырех матричных уравнений относительно четырех неизвестных вектор-столбцов Г, a, a, T, она не может быть решена, поскольку в ее состав входят прямоугольные матрицы. Отметим также, что все интегра- лы, определяющие значения элементов матриц из (12), легко берутся аналитически.

Исключив в (12) неизвестные вектор-столбцы г, T, получим два матричных уравнения отно- сительно a, a:

R ^{( 0 )} ■ a + Q ^{( 0 )} ■ R ^{( 0 )} ■ a = I ^{( 0 )}+ Q ^{( 0 )} ■ I ^{( 0 )}, [ J X N ] [ N ] [ J X M ] [ M X N ] [ N ] [ J ] [ J X M ] [ M ]

R ^{( 1 )} ■ a - Q ^{( 1 )} Q ^{( 1 )} ■ a = 0.

[ J X N ] [ N ] [ J X M ][ M X N ] [ N ]

Таким образом,

получили систему из трех

матричных уравнений (8) и (13) относительно неизвестных вектор-столбцов a и a. При этом уравнения (8) при N ^ » обеспечивают выполнение уравнений Максвелла в области плавного перехода, а уравнения (13) – выполнение граничных условий при z = [0; L].

Совместное рассмотрение (8) и (13) представляет собой, в сущности, запись обобщенной матрицы рассеяния переходного участка волновода с граничными условиями на сечениях z = 0 и z = L этого участка.

В результате объединения уравнений (8) и (13) получаем неоднородное матричное уравнение:

X

H

J б ( x , z ) sin ( a n x ) sin ( a q x ) dx

_ 0

L

J ^sin ( Y n z ) cos ( ^Y q^z ) F q , n ( ^z ) dz ,

^-

где

dz =

a

a

К = R ^{( 1 )}

S

I ^{( 0 )}-

[ J ]

Q ^{( 0 )} I ^{( 0 )} [ J X M ] [ м ]

R ^{( 0 )} - Q ^{( 0 )} R ^{( 0 )}

[ J X N ] [ J X M ][ м X N ]

Q ^{( 1 )} Q ^{( 1 )}

[ J X м ][ M X N ] S

Решая неоднородное уравнение (14), получаем амплитудные коэффициенты волн, возбуждаемых на неоднородном участке планарного вол-

новода.

Отметим ряд вычислительных особенностей представленного алгоритма, существенно снижающих временные затраты на проведение машинного расчета.

Во-первых, из анализа интегралов (9) следует, что от значения функции б ( x , z ) зависят только интегралы W ^{( 0 )}, W ^{( 1 )}, W ^{( 0 )}, W ^{( 1 )} (остальные интегралы легко берутся аналитически),

w^{( 1 )} q , n

X

L

J cos ( Y n z ) cos ( y q z ) x 0

h

J б ( x , z ) sin ( a n x ) sin ( a q x ) dx

_ 0

L

J cos ( Y n z ) cos ( y q z ) F q , n ( z ) dz .

dz =

где

H

F q , _n ( z ) = J б ( x , z ) sin ( a _nx ) sin ( a q x ) dx .

Таким образом, при вычислении четырех интегралов (15) достаточно лишь один раз рассчитать функцию F q _n ( z ) , что обеспечивает высокое быстродействие предложенного алгоритма.

Во-вторых, все интегралы, определяющие значения элементов матриц из (12), легко бе-

рутся аналитически.

Кроме того, видно, что матрицы, определяемы интегралами (9), не зависят от частоты, что позволяет вычислить их один раз и подставлять затем в (8).

причем их можно переписать в виде

L

^Wq ⁰ n = J ^sin ( Y n z ) ^sin ( Y q z ) ^X

X

H

J б ( x , z ) sin ( a n x ) sin ( a q x ) dx dz =

L 0

L

= J sin ( Y n z ) sin ( Y q z ) F q , n ( ^z ) ^dz ,

L

^Wq ⁰ n = J cos (^Y n z ) ^sin ( y q z ) ^X

X

H

J б ( x , z ) sin ( a n x ) sin ( a q X ) dx dz =

_ 0                                                  _

L

= J cos (^Y n z ) sin ( Y q z ) F q , n ( ^z ) dz , 0

L

W n = J sin ( Y n z ) cos ( ^Y q z ) ^X

• 2. Реализация метода на примере расчета плавного перехода

с экспоненциально изменяющимся диэлектрическим заполнением

Проведем расчет дифракции Н-волны на плавном переходе между планарными волноводами с частичным диэлектрическим заполнением экспоненциального профиля (параметры рассматриваемой структуры приведены на рис. 2).

При использовании МЧО плавный переход заменяется на ступенчатую структуру (рис. 2, а ) с произвольным числом областей, после чего для каждой частичной области находятся собственные волны. В результате приравнивания тангенциальных компонент поля на границах раздела частичных областей и использования условий ортогональности собственных функций поперечных сечений получается расчетный алгоритм. Детальное описание алгоритма расчета плавных переходов методом их ступенчатой аппроксимации приведено в [13].

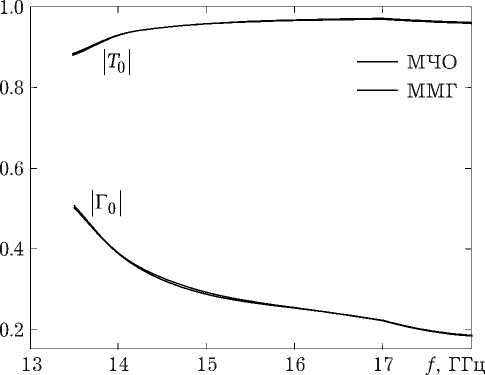
Рис. 3. Расчет плавного перехода с помощью МЧО и спектрального метода

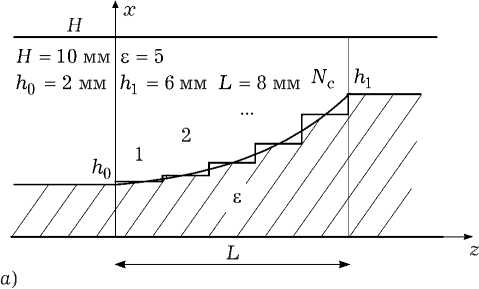
Рис. 2. Расчет дифракции на плавном переходе с помощью МЧО и спектрального метода: а ) результаты МЧО; б ) результаты спектрального метода

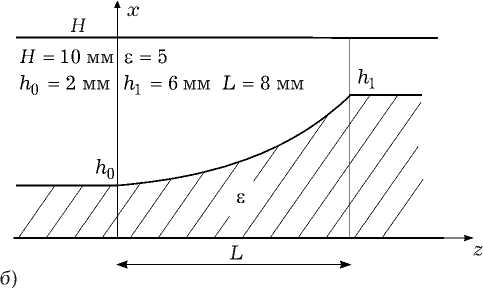
Недостатком МЧО в данном случае является необходимость расчета спектров собственных волн всех частичных областей (которых может быть достаточно много). При сложном профиле распределения диэлектрической проницаемости (подобном представленному на рис. 1) эта задача достаточно трудно реализуема. Для предложенного в данной работе спектрального метода никаких ограничений на функцию б ( x, z ) не накладывается, а распределение поля в области перехода определяется автоматически.

Результаты расчета плавного перехода, полученные с помощью МЧО и спектрального метода, приведены на рис. 3.

Из рисунка видно, что линии, полученные двумя методами, практически неразличимы, что подтверждает работоспособность предложенного метода.

Заключение

На основе спектрального метода предложен подход к решению внутренних задач дифракции, позволяющий рассчитывать характеристи- ки передачи произвольных неоднородностей в экранированных волноводах.

Представленный подход может быть распространен на задачи дифракции на неоднородностях в прямоугольных и круглых волноводах с произвольным диэлектрическим заполнением, для которых известен полный набор собственных краевых задач при их (волноводах) однородном заполнении. При расчете дифракции в волноводах, спектр которых содержит комплексные волны [1; 13], применение предложенного метода позволит избавиться от сложной процедуры поиска комплексных волн в переходе, достаточно будет рассчитать полный спектр волн правого и левого волноводов.