Спектры скрытых периодичностей геоэлектромагнитных и сейсмических событий

В работе [Зотов, Гульельми, 2010] описано явление синхронизма, обнаруженное авторами в динамической системе магнитосфера – техносфера – литосфера. Оно проявляется в виде так называемых эффектов часовых меток и выходных дней. Сущность эффектов состоит в слабой, но строго периодической модуляции геоэлектромагнитных волн Рс1 и землетрясений, синхронизированной по часам UT и по дням недели. Оба эффекта убедительно свидетельствуют о перманентном силовом воздействии техносферы на магнитосферу и литосферу.

Ранее данное явление изучалось методом синхронного детектирования, который представляет собой специализированную версию метода наложенных эпох и позволяет выявлять скрытые периодичности в длинных рядах непрерывных наблюдений. Вполне естественно попытаться исследовать это явление и другим методом, а именно методом спектрального анализа. В настоящей работе представлен результат такого исследования.

В качестве исходных данных нами использованы те же каталоги волн Рс1 и землетрясений, что и в работе [Зотов, Гульельми, 2010]. Ниже будет показано, что спектральный анализ свидетельствует о наличии четких максимумов в спектрах активности магнитосферных волн Рс1 и в последовательности землетрясений на частотах, соответствующих периодам 7 сут, 1 ч и 15 мин. Это вполне соответствует тому, что было обнаружено ранее методом синхронного накопления. Вместе с тем спектральный анализ позволил обнаружить неизвестные ранее особенности волновой активности геосфер. Внимания заслуживает некоторый подъем активности Рс1 в диапазоне периодов 50–60 мин, по-видимому не связанный с индустриальной активностью. Но особо примечательным является спектральный пик сейсмической активности, соответствующий периодичности 54 мин. Период 54 мин совпадает с фундаментальным периодом собственных сфероидальных колебаний Земли.

Магнитосферные волны Рс1

Опишем результат спектрального анализа гео-электромагнитных волн Рс1 (о магнитосферном происхождении волн Рс1 см., например, [Гульельми, Троицкая, 1973; Guglielmi, Pokhotelov, 1996]). Исходные данные мы заимствуем из каталога Матвеевой [], составленного по наблюдениям Рс1 в обс. Борок (58.03° N, 38.97° E) с 1958 по 1992 г. Всего за 35 лет зарегистрировано 17 058 серий колебаний Рс1 общей продолжительностью 18 500 ч. Для анализа мы используем моменты начала серий Рс1, указанные в каталоге с точностью до одной минуты.

Припишем каждой минуте 35-летнего интервала либо единицу, либо нуль в зависимости от того, было или не было в данную минуту зарегистрировано начало серии Рс1. Таким образом, активность Рс1 будет представлена в виде совокупности N дискретных событий, произошедших на большом, но конечном отрезке времени. Введем функцию n ( t ), характеризующую динамику волновой активности, причем

∞

J n ( t ) dt = N.

-∞

Разложим n ( t ) в интеграл Фурье:

∞           dω

n ⁽ t ) = n _m exp⁽ - i m t )—.

-^J„              ²ⁿ

Компонента Фурье nω определяется формулой to nm = j n(t)exp(itot)dt.                             (3)

-to

По определению

N

n ⁽ t ) = Z ⁵ ( t - t j ) .                                  ⁽⁴⁾

j = 1

Здесь t j – начало минутного интервала, которому приписано число 1, N – общее число таких интервалов, как это было указано выше. Подставляя (4) в (3), находим компоненты Фурье:

N n m=E exp (iю tj )•                             (5)

j = 1

На рис. 1 показан результат расчета интенсивности компонент Фурье | и _ш |² (здесь и ниже безразмерная величина n _ш|² выражена в единицах 10⁴). По-видимому, спектр воспроизводит так называемый эффект часовых меток, выявленный в работе [Гульельми, Зотов, 2010] методом синхронного накопления. Отчетливо различим пик спектральной интенсивности с периодом 15 мин. Любопытно, что в диапазоне периодов 45–70 мин (0.24–0.37 мГц) выделяется амплитуда вариации с периодом 53 мин (0.314 мГц). О пике на частоте 0.277 мГц (что соответствует периоду 1 ч) судить трудно. Скорее, следует говорить о некотором подъеме спектральной интенсивности на периодах 50–60 мин, по-видимому никак не связанном с индустриальной активностью. Вопрос о его возможном происхождении мы обсудим ниже.

Эффект выходных дней, обнаруженный ранее методом синхронного накопления [Fraser-Smith, 1979; Guglielmi, Zotov, 2007], воспроизводится на рис. 2 в виде максимума интенсивности компонент Фурье | n_T |² на периоде T = 2л/ю, равном 168 ч. Происхождение дополнительных пиков, заметных на рис. 2, не вполне ясно.

Землетрясения

Перейдем к спектральному анализу последовательности землетрясений. Подобно тому, как это сделано в работе [Зотов, Гульельми, 2010], исходную информацию мы заимствуем из каталогов зем-

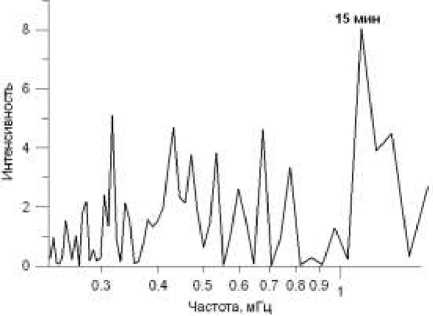
Рис. 1. Спектр активности магнитосферных волн Рс1 (эффект часовых меток).

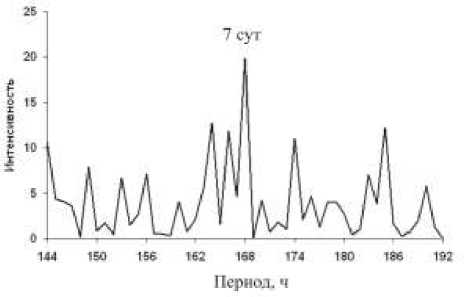
Рис. 2. Спектр активности магнитосферных волн Рс1 (эффект выходных дней).

летрясений Международного сейсмологического центра ISC [] и Национального информационного центра геологической службы США USGS/NEIC [ ]. Мы припишем каждой секунде интервала, выбранного для анализа, либо нуль, если по каталогу в данную секунду не было землетрясений, либо целое положительное число νj, если где-нибудь произошло νj землетрясений. Чтобы сделать спектральный анализ глобальной сейсмичности, представим динамику землетрясений в виде ряда

N

n ⁽ t ) = Е v j ^{5 (} t - t j ), ⁽⁶⁾ j = 1

аналогичного ряду (4), который был использован при анализе Рс1. Здесь t j – начало секундного интервала, которому приписано число ν j , N – общее число таких интервалов. В результате вместо (5) будем иметь

N n Ш=Еv j exp (ito tj). (7) j=1

Для воспроизведения эффекта часовых меток построим спектр сейсмической активности по данным каталога USGS с 1973 по 2010 г. Общее количество землетрясений с магнитудами М > 1, которые учтены в каталоге за 38 лет, равно 536 000. На рис. 3 показана интенсивность компонент Фурье n _m|². Отчетливо видны ожидавшиеся пики в спектре на частотах 0.277 и 1.11 мГц. Они соответствуют часовой и 15-минутной периодичностям, обнаруженным ранее в работе [Зотов, Гульельми, 2010] методом синхронного детектирования.

Новым и неожиданным является мощный пик на частоте 0.309 мГц. Данная частота соответствует периоду 54 мин, совпадающему с периодом колебаний Земли ₀ S ₂. Физический смысл такого совпадения мы обсудим в следующем разделе.

На рис. 4 показана интенсивность компонент Фурье | n_T |², где T =2π/ω – период колебаний. Спектр построен по данным каталога ISC. В период с 1964 по 2006 г. зарегистрировано 2 300 000 землетрясений с магнитудами М ≤5. Главный максимум в спектре на периоде 168 ч соответствует эффекту выходных дней, обнаруженному ранее методом синхронного детектирования [Зотов, 2007]. Имеется также дополнительный максимум на периоде 188 ч неясной этиологии.

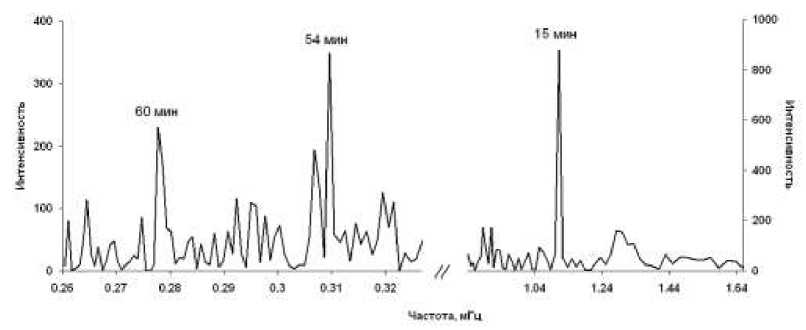
Рис. 3. Спектр активности землетрясений (эффект часовых меток).

О колебаниях Солнца и Земли

В данном разделе мы обсудим вопрос о модуляции магнитосферных волн Рс1 и землетрясений с периодами модуляции, близкими к одному часу. В отличие от строго часовой периодичности, происхождение которой мы связываем с человеческим фактором [Зотов, Гульельми, 2011], околочасовые периодичности, несомненно, вызваны естественными причинами. Мы рассмотрим возможное влияние собственных колебаний Земли и Солнца с периодами, близкими к одному часу, на магнитосферную и литосферную активность.

Вначале рассмотрим геоэлектромагнитные волны. Известно, что тороидальные колебания Земли индуцируют колебания геомагнитного поля. Этот довольно слабый эффект был зарегистрирован после Чилийского землетрясения 1960 г. [Winch et al., 1963]. Маловероятно, что он имеет какое-либо отношение к околочасовым колебаниям активности магнитосферных волн Рс1. Более интересны в связи с этим крупномасштабные колебания солнечной поверхности [Воронцов, Жарков, 1981]. Известно, что Кобрин и Коршунов обнаружили в 1972 г. колебания Солнца с периодом около 50 мин по наблюдениям солнечного радиоизлучения на длине волны 3 см [Кобрин и др., 1973]. В свое время вопрос о геоэффективности колебаний Солнца оживленно обсуждался в работах [Гульельми и др., 1977; Toth, 1977; Lanzerotti, MacLennan, 1978]. Для нас особый интерес представляют периоды 50–60 мин, которые были отмечены в спектрах колебаний солнечной поверхности, вариаций АЕ -индекса и огибающей ампли-

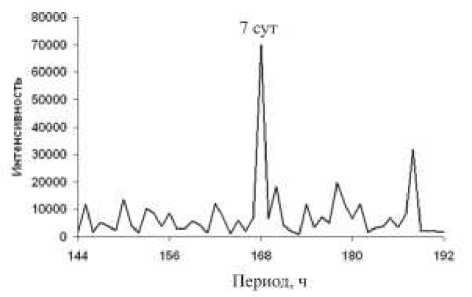
Рис. 4. Спектр активности землетрясений (эффект выходных дней).

туды геоэлектромагнитных волн Рс3 [Гульельми и др., 1977]. На рис. 1 мы видим некоторое повышение спектральной плотности в диапазоне частот, соответствующих периодам 50–60 мин. Однако следует признать, что этого все же недостаточно для того, чтобы обоснованно судить о модуляции волн Рс1 колебаниями солнечной поверхности.

В спектре сейсмической активности на рис. 3 наблюдается пик на частоте 0.277 мГц, имеющий явно антропогенное происхождение (эффект часовых меток). Вместе с этим наблюдается и более мощный пик на частоте 0.309 мГц, соответствующей периоду 54 мин. Период 54 мин совпадает с периодом фундаментальной моды 0 S 2 собственных сфероидальных колебаний Земли (о тороидальных и сфероидальных колебаниях Земли см. в [Аки, Ричардс, 1983; Жарков, 1983; Кузнецов, 1997]). Напрашивается гипотеза, что колебания Земли как целого приводят к модуляции активности землетрясений. Наша гипотеза основана на представлении о так называемой наведенной (индуцированной) сейсмичности (о наведенной сейсмичности см., например, [Николаев, Верещагина, 1991; Адушкин, Турунтаев, 2005]).

Из общих соображений разумно предположить, что эффект модуляции, о котором идет речь, должен проявляться прежде всего в тех местах, где напряженно-деформированное состояние земной коры близко к порогу, за которым происходит магистральный разрыв горных пород и возникает землетрясение. Из-за непредсказуемости землетрясений трудно заранее отыскивать такие места. Поэтому мы поступим следующим образом: выберем эпицен-тральную зону сильного землетрясения и будем искать эффект модуляции в последовательности афтершоков с достаточно большой магнитудой в этой зоне. Сам факт возникновения сильного землетрясения свидетельствует о переходе через указанный выше порог, а появление афтершоков большой магнитуды говорит о том, что главный удар не снял полностью накопленного напряжения горных пород. Мы отобрали из каталога USGS за период с 1973 по 2010 г. 500 сильных землетрясений с магнитудами М>7, учли все афтершоки с магнитудами 6<М<7 в эпицентральных зонах радиусом 10° и применили метод наложенных эпох, взяв за нулевую точку отсчета времени момент возникновения сильного землетрясения.

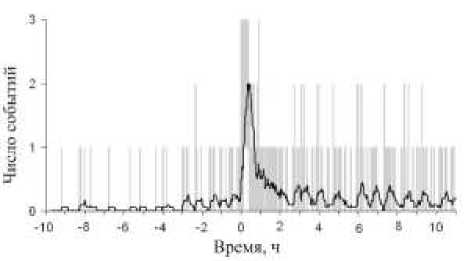
Рис. 5. Динамика форшоков и афтершоков с магнитудами 6≤ М <7 в эпицентральных зонах сильных землетрясений ( М ≥ 7). Толстая кривая получена сглаживанием исходных данных по 20 точкам.

Результат показан на рис. 5. Мы видим, что морфологически эволюцию сейсмичности после главного удара естественно разделить на два этапа. Мы будем называть их этапом спонтанной и этапом вынужденной активности афтершоков (ориентировочно 0–2.5 ч и 2.5–10 ч соответственно). Наибольшая активность наблюдается в первый час после землетрясения. Затем происходит некоторое успокоение и примерно в 2.5 ч наступает минимум активности. После этого начинается подъем, который заканчивается максимумом примерно в 3 ч. Этот максимум мы объясняем тем, что, распространяясь от эпицентра с характерной скоростью 3.7 км/с, поверхностные упругие волны совершают полный оборот вокруг Земли, возвращаются в окрестность эпицентра через 3 ч после главного удара и индуцируют здесь повторные толчки. Обратим внимание на группу затухающих осцилляций с околочасовым периодом, особенно четко выраженную в интервале 6–11 ч (рис. 5). Мы обнаружили, что спектр осцилляций имеет максимум на частоте 0.31 мГц (рис. 6). Другими словами, активность афтершоков колеблется с периодом 54 мин, который совпадает с периодом собственных колебаний Земли 0 S 2 .

Заключение

Явление синхронизма в динамической системе магнитосфера – техносфера – литосфера, обнаруженное ранее методом синхронного детектирования, в данной работе исследовано методом спектрального анализа. В спектре активности магнитосферных волн Рс1 и в спектре сейсмической активности выявлены максимумы, соответствующие недельному, часовому и пятнадцатиминутному периодам антропогенного воздействия на магнитосферу и литосферу. В ходе исследования обнаружен дополнительный максимум в спектре сейсмической активности на периоде 54 мин, свидетельствующий о воздействии сфероидальных колебаний Земли ₀ S ₂ на сейсмическую активность.

Выражаем глубокую признательность В.В. Адуш-кину, А.Д. Завьялову, Ю.И. Зецеру, С.И. Козлову, А.Н. Ляхову, А.В. Пономареву, А.С. Потапову, А.Л. Собисевичу, Л.Е. Собисевичу и Г.А. Соболеву за интерес к работе и ценные замечания. Работа выполнена при финансовой поддержке РФФИ

(грант № 10-05-00661) и Программы № 4 Президиума РАН.

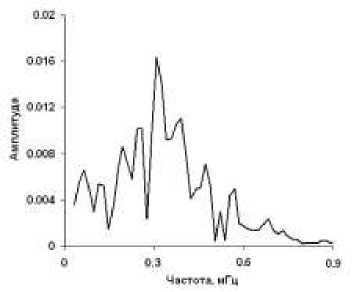
Рис. 6. Спектр усредненной активности афтершоков (черная кривая на рис. 5) в интервале 2–11 ч после главного удара.