Spherical symmetric solutions of F(R) gravity with a kinetic curvature scalar

The fact that Universe expansion is accelerating at the present time is confirmed by various observations such as measurements from supernovae [1] ， [2], cosmic microwave background (CMB) radiation [3], [4], [5], large scale structure [6], baryon acoustic oscillation [7] and weak lensing [8]. One of the way to explain the observed acceleration of the Universe is to develop alternative (modified) theories of gravity which can be reduced to GR on some scales but can lead to Universe acceleration on very large scales. For recent reviews of modified theories of gravity, see, for instance, [9], [10], [11] and the fundamental work [12].

The growing interest to modified theory of gravity is due to detection of gravitational waves are emitted by the system of two black holes (BHs) which allows to test extensions of the GR theory [13]. Therefore, besides of cosmological applications of modified gravity theories, it is of interest to study spherically symmetric solutions as possible resulting BH which generates gravitational waves, may be with other characteristics then in GR. In our present investigation we analyze spherically symmetric solutions in the theory of gravity with high-order corrections to scalar curvature.

Modifications of GR that include higher-order curvature corrections to the Einstein-Hilbert action have a natural explanation, related to taking into account quantum effects in the low-energy limit of string theory, superstrings, and supergravity, needed for the construction of a quantum theory of gravity [14].

We can mention that a prominent example of application of quantum corrections to GR, with derivatives up to fourth order, has been demonstrated by A. Starobinsky [15] in cosmology. It was shown that such corrections may control an accelerated expansion of the Universe at its early stage of evolution (inflation).

This kind of models has been developed towards considering 6th-order corrections in theories of gravity of the kind R + qA ² + yRDR, where q and 7 are some constants, and the additional terms that modify the Einstein theory were, with the aid of conformal transformations of the metric, put into correspondence to certain effective scalar fields [16]- [20], which led to a two-field treatment of such models. Also, in [21] the correction RDR was treated as a small perturbation, and its influence on the parameters of cosmological perturbations was studied.

Inclusion of higher derivatives to modified theories of gravity is also caused by the necessity of introducing such corrections at renormalization of the stress-energy tensors of quantum fields in the framework of the semiclassical approach to gravity [22].

In the article [23] it was shown the way how to reduce theory of gravity which contain in the action the Ricci scalar and its first and second derivatives to GR minimally coupled to few scalar fields. For special choices of functional dependence /(R, (VR)2, DR) it is possible to reduce the theory to chiral cosmological model. One such example and its application in cosmology is demonstrated in [25], [26], [27].

In the work [27] the study of the model, using the technique described in [23], [24], was continue. There were carried out a similar transition to a scalar-tensor theory by introducing Lagrangian multipliers and the arising auxiliary fields. Using a conformal transformation from the Jordan frame to the Einstein one there were obtained that the model can be represented as a two-component nonlinear sigma model with an interaction potential. Such model is named as a chiral cosmological model (CCM) for consideration in cosmology. Because in our present work we deal with gravitation in spherically symmetric spacetime, not in cosmology, the model with the action s = /，-id4c (Ц — 2hAB 3，L4g^ - W3), ⑴ we will call Chiral Self-Gravitating Model (CSGM). It is clear that CCM is the case of CSGM in cosmological spaces. Thus, the main goal of our investigation is to find conditions to have exact static, spherically symmetric solutions in the CSGM.

The article is organised as follow. In Sec. 2 we represent the action of the /(A) gravity with kinetic curvature scalar in Einstein's frame and give connection of the model to CSGM. The Sec. 2 is devoted to tensor equations of CSGM in metric spacetime which represented in Sec. 3 for spherically symmetric spacetime in harmonic coordinates. Sec. 4 contains the gravitation and fields equation in spherically symmetric spacetime in harmonic coordinate. In Sec. 5 we consider the case of scaling transformation when the model transforms from Jordan to Einstein frame and the representative function /1 of the scalar field 0 is chosen as GR analog, namely /i(0) = 0/2. For this case it was found the three classes of solutions for gravitational field and demonstrated the method of determination of kinetic function X(0) corresponding to known scalar field dependence on analog to radial coordinate u. Sec. 6 devoted to investigation of the model subject to special relation (ansatz) between metric components. Three classes of solutions are represented as well. In Conclusion we discuss obtained results and future investigations.

1.    The model in Einstein frame

In the work [23] the authors consider the most general form of /(A) gravity with higher derivatives of first and second order with respect to Ricci scalar. Such a theory of gravity is described by the action

SfRR‘ = / d%C (VA)2) ,( where

/(A, (VA)2) = /i(A) + X(A)V“AV“A.(4)

have been studied for cosmological applications in [25], [26], [27]. In (4) and hereafter /i(A) and X(A) are C ¹ functions of scalar curvat ure.

The model (3)-(4) can be transformed to Einstein scalar fields gravity [23], [27] with the action SEfRR’ = / d^x ^— gE (-^ - 2 虐 Х,нХ," + 4/i⁽⁰⁾e^-2 ^ ^2/3x - 工加 ^- ^ ²/³'

The action Se/rr，(5) can be presented in the form of a chiral cosmological model [28] with two chiral fields 夕1 = %. ^2 = 0. and 2D metric of the target space df： = d%2 — b^2/xx (0)d02.                            (6)

Also it needs to include in the model the interaction potential

爪 =1 〕 Ex ( 0 — e^- ^ ²/³' /-。 )) .                        (7)

Because in our present work we deal with gravitation in spherically symmetric spacetime, not in cosmology, the model (5) and similar ones are nothing but self-gravitating non-linear sigma model with the potential of interaction. For the sake of brevity we will refers to this type models as Chiral Self-Gravitating Model (CSGM). It is clear that CCM is the case of CSGM in cosmological spaces.

In the next section we will represent basic equation of CSGM.

• 2.    Chiral Self-Gravitating Model

The action of CSGM as the action of the self-gravitating nonlinear sigma model with the potential of (self )int eract ions W ( ( ^) [29]. [30] reads ：

Scsgm = /，-^а4T (辰 - 2кав (同д%дg"" - W(夕))，             ⑻ where 冗 being a. scalar curvature of a Riemannian manifold with the metric ^丛“(т).呂一Einstein gravitational constant,夕=(夕1,...,夕、)being a multiplett of the chiral fields (we use a notation 夕4 = d/A = l^r). Һдв being the metric of the target space (the chiral space) with the line element 曲彳=Һав (©d^Ad^B, A, В,...=讣.                       (9)

The energy-momentum tensor for the model (8) reads

T“" = hAB屮亡屮B - 9“" (2尺嵋9“°hAB + W3).(1

The Einstein equation can be represented in the form

%" = к{Һав 8 Als § + 9“"W 3}(11)

which simplify the derivation of gravitational dynamic equations.

Varying the action (8) with respect to gc, one can derive the dynamic equations of the chiral fields

/— di(V-ŠhABgW8A) -    B； 8c1sB9“" - W,A = o,(12)

-g2 where W,a = dd^- Considering the action (8) in the framework of cosmological spaces we arrive to a chiral cosmological model [28], [29], [30], [31], [32], [33].

• 3.    CSGM in spherically symmetric spacetime

The standard representation of the spherically symmetric spacetime without gauge specification is [34]

ds2 = -£2"(u)必2 + £2Mu)du2 + £2伙В (d^2 + Sin2 %82)

Let us choose the harmonic coordinates where we have the connection between metric function of the form

A = 2/ + 〃

Einstein equations (11) can be derived based on components of Ricci tensor and they are:

e-4%〃 = -ке2"卜-V273X(0 - e-^/^/K* ,(15)

-2/’’ - / + 2(/‘)2 + 4/’J = к (hii(х')2 - е-^/^Х(。)(。')2 + е4°+2"4е-^23* (。- е-^2/3""。)))，

1 — /‘‘exp [-2/ — 2〃] = ке2^；е-■х (о - e-V273x/i(0)) .(17)

Chiral fields equations after substitution of metric components and the potential yield hiix’’ -七е Y*X(0)(0‘)2 - e4^+2"

-六 eY х⁰ + 七产遅 -(0)

o,

| х (0)0‘х‘ + 2 х ； (0‘)² + Х(0)0" + 4е⁴°+2" (1 - е Ү*/i,j = 0.          (19)

From equations (15) and (17) one can obtain the relation which make restriction on the metric components

/ 〃- / = е²0+²"

• 4.    The case of scaling transformation

Following by special suggestion in cosmology [24], [27] let us study the case when the scalar field X is equal to special constant x = - J2ln 2- This value of x corresponded to identical conformal transformation with Q2 = 1.

The gravitational and chiral field equations will take the following form e-(4°+2%〃 = —к (。/2-/i(。)),

-2/3" - J，+ 2(0)2 + 4/3” = к (-2X(。)(“)2 + e4°+2"(ф^2 - /і(<^))) ,

1 — 3〃e-2”2" = ке2°(ф/2- һ(ф»,(23)

-2Х(ф)(ф，)2 - е4°+2"(-ф + 4/і(ф)) = 0,(24)

2Х(ф)ф〃 + X；(ф，)2 + е4^+2-(1/2 - /і,ф) = 0.(25)

The equation (24) may be considered as additional one, for the model with one field ф this equation will not appear (no variation on %).

• 4.1.    Case 力( 0) = ф/2

Such suggestion bring the model close to GR, if we additionally set X(ф) = 0. For the case /і(ф) = ф/2 we have the system of equations

〃“ =0 , 〃 = 人 1 & + 人 2 , ^1, ^- 2 - const.,                            (26)

-2/3 〃 + 2(3 ， )² + 40-1 = к (-2X(ф)(ф ‘ )²) ,                         (27)

1 - 3 〃 e

— 2Q — 2Hi 〃 一 2H2

0,

2X (ф)ф，，+ X； (ф，)2 = 0.(29)

• 4.1.1    The solutions of the auxiliary equation

Let us study solutions of the equation g，，(u) = Q£2。", @,b — const.,(30)

which we will use for special values of parameters later on.

The first integral of (30) is

®，)2 =+ Q.(31)

There are three possibilities according with Ci value.

• •    Ci =0

  The solution is

  
  

g(u) = — 6 ln ^±Vft6(u — u * )),

where the integration constant u* may change the sign of the argument (u — u*).

• •    G = м2 > 0

The solution for this case is

y(u)=干〃u - yin (- ： + 六 е2。"") .

6 b4/22

From here we set u = u - u* to simplify the expressions.

• •    Ci = - Q2 < 0

• 4.1.2    Solutions of the model

The solution is y(u) = - 11n \B—^^] .(34)

6        q cos(abu) 丿

The equation (28) can be reduced to y〃 = 2〃(35)

by the substitution y = 2/ + 2Aiu + 2^2.(36)

Thus we have three solutions for y(u) by setting in the solutions above q = 2, 6 =1/2.

• •    Ci = 0

The solution is

y(u) = -21n(u).(

From here one can find

/(u) = - 1n(u) - Aiu - A2.(38)

Equation (27) gives kX (0)(“)2 = A1.(39)

Thus we can represent class of solutions by giving 0 = 0(u).

In literature [34] one can find the following type of solutions for the scalar field

0i (u) = a*u + 0*, 02(u) = /* tanh(A*u)(40)

and                                   ______

03(u) = D arctan --------+0*, O,p = const.(41)

P

Here the letters with lower star mean constant. Note that the function /1 (0) can be easy restored for given 0 as

/i(0)=20.

Note that the potential for this case is equal to zero and we deal with massless scalar field.

It is easy to define the function X(0) for each case. The sign of kinetic function X(0) corresponds to type of the scalar field: canonical, if X < 0, and phantom, if X > 0. Thus we have corresponding to the scalar fields kinetic functions:

—「  A2—

Xi(0i) =    = const.(42)

KQ*

X2(02)= K；* (/2- 02(u)) 2 .(43)

Хз(0з) = Ag tan2 ( ^(^ )(1+tan2 (^3(^))."

• •    d = м2 > 0

  The solution for this case is
  	У （ 〃 ） =		干 儿〃 — ln (— 2 +	3е2""). 4 〃 2/			(45)
  From here one can find
  / ( 〃 ) =	1 — 2	干 儿〃	- ln (-2 +白日)		- 74]и -	-/2.	(46)

Equation (27) gives кХ(°)(")2 = - (М2 -看)

The solutions for kinetic function Х(0) are

(掰 - )

Хі(0і) =  -----5- = const.(48)

KQ*

1     4*

Х2(02)=    к『   (段-02®)  .(49

Хз(0з)=。二)一 tan2 (^03^ )(1+tan2 ( 03^)) .(50)

• • 。 1 = - Q2 < 0

The solution is

( 1 Q

2J ).

From here one can find

/(^ulnj^co^ )-4〃 一A.(52)

Equation (27) gives кХ (0)(0')2 = 丁 + 普.

The solutions for kinetic function Х(0) are

Xi(0i)

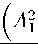
+ 圖 KQ*

const.

^Х2⁽⁰2 )

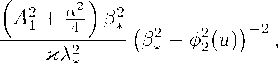
Хз(0з) = О¹ ： ” tan² (^^)(1 + tan² (^^)) .     (56)

It should be stressed that equation (29) is satisfied when Х(0)(0‘)² = const. Indeed, taking the derivative with rrespect to 〃 from both part of equations (39),(47) and (53) one can find Х‘(0‘)³ = -2Х0'0" and equation (29) is automatically satisfied.

Thus we can state that Х(0)(0‘)² = const. with (26), (38), (46) and (52) give us three solutions. Therefore for each given dependence of the scalar field 0 as function on 〃 one can define the kinetic function Х(0) which holds the solution. Examples of such solutions we described above.

5.    Ansatz /3 = mp

Choosing the relation between metric functions

/3 = my, m = const.                                   (57)

we can solve the equation (20) which takes the following form

J' =        e²"^(m+1 ) .                                          (58)

m — 1

So we can use the solutions of auxiliary equation (30) with g = “ and a =——^―j-, b = m + 1, m = 1, m = —1.

With the ansatz (57) and choosing the /1(0) as

/1 (0) = 0/2 + K2/2(0), K2 = const.,(59)

the gravitational and field equations take the following form e-2(2m+1)" / = кК2 /2(0),(60)

—(2m + 1)/ + 2m(m + 2)(J)2 = к (—2X(0)(0')2 — e2(2m+1)"^2/2(0)) ,(61)

1 — mz/‘e^-2 ( ^m+1 ) “ = —ке^2пг" ^2/2(0 ) ,

2X (0)0〃 + X； (0‘)2 — e2(2™+1)-K2/20 = 0.(63)

Taking into account (58) equation (60) leads to

/2(0) =             e-2 小.(64)

KK2(m — 1)

Substitution (64) into (62) gives the identity. Also substitution (64) into (61) leads to

-(2m + 1)" " + 2m(m + 2)("')2 +..-..ё2(m+1)^ = —2кx (0)(0‘)2.(65)

m — 1

Thus we can find the dependence / 2 = / 2(0( 〃 ) ) = / 2З) from (64) using known the solutions of equation (58) on the basis of auxiliary equation solutions (4.1.1).

We can obtain the general form for the combination X(0)(0‘)² if we insert 〃“ from (58) and using the first integral of (58)

" ‘ ² =        e^{2(m+1 ) !/} + C1                                    (66)

m2 — 1

into equation (61). The result is

2m m2 — 1

e^2(m+1)" + 2m(m + 2)C₁ = — 2 k X (0)(0‘)².

Let us note that we can not obtain the constant combination X(0)(0‘)2 = const. for real m. Thus the case considered in previous section is not compatible with ansatz approach.

5.1.    The solution Ci = 0

We may consider two branches of solution in this case. Namely

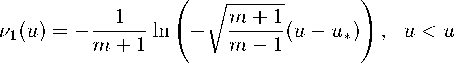
〃 2 （ U ）

m + 1

In

(不…)

〃 > 〃 * ,

where u* is an integration constant.

From (21) we obtain

"°)= Кк2^ 产"

Substituting the solution (68) and (69) in (70) one can find

/2 ( °) = (кК2 ( т - 1))^-1 ( m + 1 ) (u - u * )2

■m

■m+1

Substituting the solution (68) and (69) in (67) one can find

X (°)(“)2

2m

2K(m + 1)²(u — u * )²

Ones again, let us define the kinetic function for scalar field (40) and (41).

^X(°1 ) = ― 2к(т + 1)²(°i(u) — ° * )² ,

X (°2 )

__________ 2m— __________

2K(m + 1)²(/32 — °2)²(tanh ^{- 1}(°2// * )²

Here tanh ^{- 1} 力 :=arctanh x.

^X3 （ °3 ）

2m tan²((°3 — ° * )/D) 2K(m + 1)²D²p²

Corresponding solutions for /2(°) are

m                2 m

/2(°і) = (K&(m — 1)) ^{- 1} У i (°1M-° * ) i m — 1J \ a*    /

/2(°2 ) = (KK2(m — 1)) ^{- 1}

m                        2 m

[m^ 厂(土 tanh ^- 1( * ))E

/2(°з) = (KK2(m — 1)) ^{- 1}

m + 1

m — 1

m m +1

2m r -

1                      m + 1

• —cos(°3(u) — ° * )

• #                  J

• 5.2.    The solution Ci = /і² > 0

From the presentation (59) it is clear that the function /2(°) gives, in some sense, the deviation from GR. Thus we can see from (76)-(78) various functional possible addition, keeping in mind exchange ° T 兄

The solution

""* = 干通 +1Лm¹ⁿ

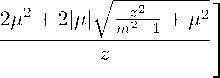
z = _e ( ^m+1 ) ^

must be inversed in order to find the solution for 〃 (u). From (79) one can obtain

"=〃“——Ц1П (^+! + ：e2“g+1)q .

m + 1  \m - 1  〃2

Then from (67) we find

2Kx(。)(“)2 = - [4ml 1 /               — 2〃2m(m + 2),

I^m2 - ^d ( 心 + E1®)

where

Ei(u) = e²"^(m+1 ) u.

Thus we can state that for each given 0(u) = const. there are exist X(0), obtained from (81) and which gives the exact solution with

2 m ^ +1

/2 ( ° ( ^u)) = Ki^m-D e"“ (m-i + L ( ^u))   .             ( 82 )

Inverting the dependence 0 on u as u(0) the dependence /2 оn 0 will be restored. The kinetic function X(0) can be defined by algorithm described in Sec. 5.2

• 5.3.    The solution Ci = —a²< 0

The solution u - u* =干———+ ])arctan

/「 I , z = eg+D",(83)

• V e + a² /

must be inversed in order to find the solution for 〃 (u). From (83) one can obtain

〃(u)=—-——1n [(m + l)a (1 ± tan2(a(m + 1)u))"| .(84)

m +1    (m — 1)J

We can obtain/2(03)) from (64)

/2(0(u))= [a2(m — 1)(1 士 tan2(a(m + 1)u))] m+1 (KK2(m — 1))一 .(85)

From (67) one can find

2kX(0)(0‘)2 = —a42m(m2 — 1) [1 士 tan2(a(m + 1)u)]2 — 2a2m(m + 2).(86)

Inverting the dependence 0 on u as u(0) the dependence /2 оn 0 will be restored. The kinetic function X(0) can be defined by algorithm described in Sec. 5.2

Conclusion

In this paper we presented an analysis of non-linear self-gravitating sigma model with the potential of interaction (chiral self-gravitating model) of /(A) gravity with a kinetic curvature scalar in a spherically symmetric spacetime. We derived the modeFs equation in harmonic coordinates and found restriction on the metric components for this case. For the case of scaling transformation, when Weil conformal function is equal to one, it was found metric components for the case when /i(0) = 0/2 and pointed out the method of definition the kinetic function X(0) if the dependence of scalar field 0 on radial-like coordinate u is known. New solutions for the metric components and explanation of kinetic function X(0) derivation were founded for special relation between metric components (ansatz) В = mu, m = const. Further we plan to consider geometrical structure of obtained solutions such as horizons and singularities.

Acknowledgments

• S.V.C. is thankful to CNPq for support his visit to Brazil, Vitoria, UFES, where the work was finalised. J.C.F. thanks CNPq (Brazil) and FAPES (Brazil). S.V.C. and F.I.V. are thankful for the financial support of RFBR by grant 20-02-00280-A. S.V.C. is grateful for the support of the Program of Competitive Growth of Kazan Federal University.

С.В.Ч. благодарит CNPq за поддержку его визита в Бразилию, г. Витория, Федеральный Университет Эспириту-Санту, в котором была выполнена данная работа. Ж.С.Ф. благодарит CNPq (Бразилия) и FAPES (Бразилия). С.В.Ч. и И.В.Ф. благодарны РФФИ за финансовую поддержку по гранту 20-02-00280-А. Также С.В.Ч. благодарен за поддержку в рамках программы повышения конкурентоспособности Казанского федерального университета.