Spins of supermassive black holes

The blistering technological progress in astronomical and astrophysical experiments provides the successful opportunity for formulation of the “Standard Astronomical and Astrophysical Model” quite like the “The Standard Model of Particle Physics”. The supermassive black holes with masses M >

10 ⁶ M э (where М _ө is the Sun mass), reside either in the centers of galaxies or at the intergalactic space, are the indispensable components of this “Standard Model”. Nowadays we have the clear qualitative understanding of the astrophysical properties of supermassive black holes owing to the huge amount of the observational data and theoretical predictions in the framework of the General Relativity [1, 2, 3, 3, 4, 5, 6, 7, 8, 9, 10, 10, 11, 12, 13, 14, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 30, 31, 33, 34, 35, 36, 37, 38, 39, 40 ? ].

The existence of hot accreting matter in the vicinity of black hole event horizons is predicted by the Blandford-Znajek mechanism [38], which is confirmed by recent General Relativistic MHD numerical simulations at the most powerful supercomputers. The basic feature of the Blandford-Znajek mechanism is the existing of electric current embracing the black hole and heating the accretion disk very near the black hole event horizon providing the main contribution to the black hole luminosity. This luminosity exceeds in many orders the corresponding luminosity from the stationary background behind the black hole. A dark spot at the black hole image in the Blandford-Znajek mechanism is a lensed image of the event horizon globe. This luminosity exceeds in many orders the corresponding luminosity from the stationary background behind the black hole.

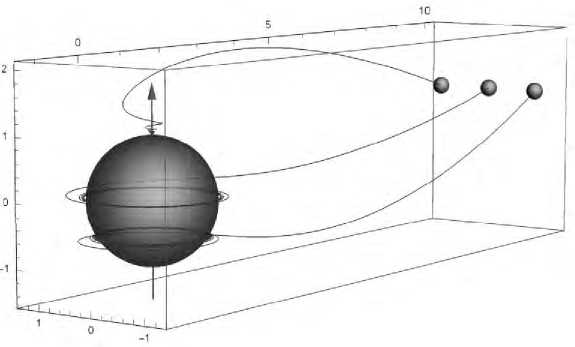
Рис. 1. The examples of 3 D numerically calculated trajectories of massive test particles, infalling into the fast rotating black hole with spin a = 1 . Particles are winding on the event horizon in the direction of the black rotation by approaching to the black hole. The dark grey sphere is the globe of the black hole event horizon. Arrow shows the direction of the black hole spin (for details see [41, 42, 43, 44, 45, 46, 47, 48, 49]).

The theoretical framework for understanding the black hole physics is the classical Einstein theory of gravity (the General Relativity) providing also the quasi-classical description of the amazing Hawking black hole evaporation. The major discoveries of last decade, related with the black holes are the direct detection of gravitational waves by the laser interferometers [1] and direct observation of the supermassive black hole images by the Event Horizon collaboration [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]. There are the plentiful publications describing the astrophysical and physical properties of black holes, including the supermassive ones. See, e. g., the subjectively chosen list of textbooks, monographs and review articles [3, 10, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40].

In this paper we describe mainly the theoretical physical concepts and observational astrophysical data related with the rotation of supermassive black holes, which is crucially important for different physical phenomena: a huge energy emission from the accreting matter, a generation of giant relativistic jets or production of High Energy Cosmic Rays (HECRs).

The numerous observational astrophysical data indicating in favour of the fast rotation of supermassive black holes in the Active Galactic Nuclei (AGNs) were obtained initially by the interferometric radio-telescopes. It was the discovery of the extremely long relativistic jets from the Active Galactic Nuclei [50, 51, 52, 53, 54]. The relativistic jets from the Active Galactic Nuclei are the

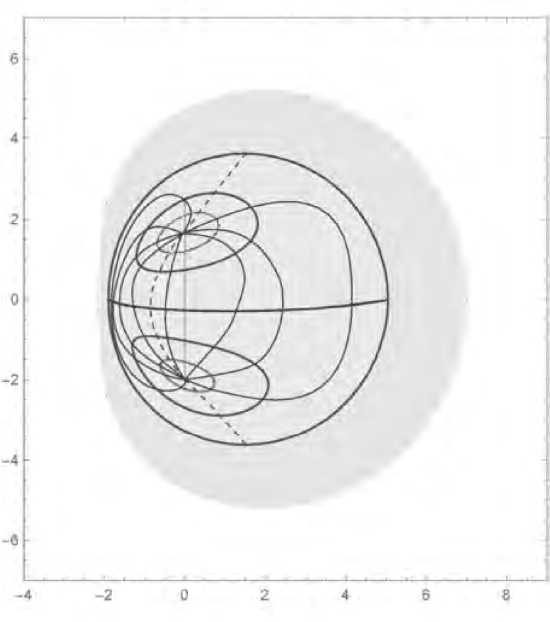
Рис. 2. A reconstruction of the lensed event horizon globus of SgrA* with distant observer a little bit above the black hole equatorial plane. The closed curves are meridians and parallels on the lensed event horizon globe. The dashed curve is the null meridian. The grey region is the position of the classical black hole shadow projected at the celestial sphere. Arrow shows the direction of the black hole spin. The dashed ring is the size of the event horizon in the imaginary Euclidean space without gravity. For more details see [41, 42, 43, 44, 45, 46, 47, 48, 49].

inevitable sources of the observable High Energy Cosmic Rays, including photons, protons, neutrinos and, possibly, the hypothesized dark matter particles [55, 56, 57, 58, 59, 60].

A dark spot at the black hole image in the Blandford-Znajek mechanism is a lensed image of the event horizon globe. We calculate numerically the form of dark spots at the black hole images by using Carter equations of motion [17] of test articles in the Kerr metric [10]. For more details see [41, 42, 43, 44, 45, 46, 47, 48, 49].

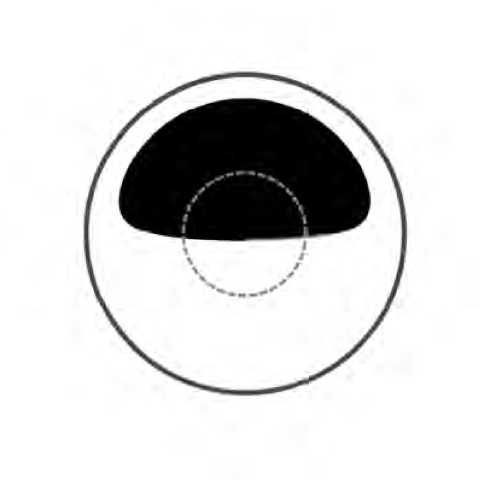
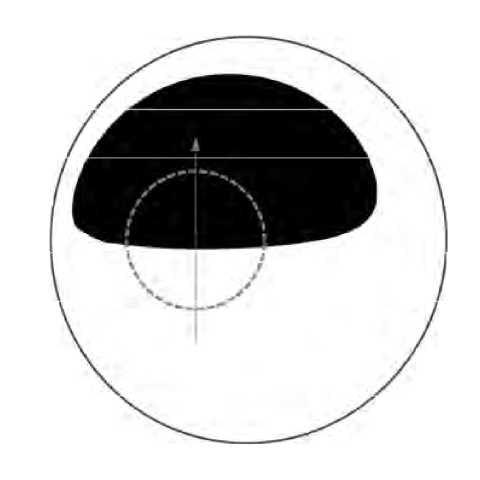
Рис. 3. Superposition of the observable image of SgrA* with the modelled dark spot at the value of spin a = 0 (left) and a = 0 . 65 (right). The closed curve is the position of the outer boundary of the classical black hole shadow at the celestial sphere. The dashed ring is the size of the event horizon in the imaginary Euclidean space without gravity.

Рис. 4. The superposition of the Event Horizon Telescope image of supermassive black hole SgrA* with the corresponding numerically modelled dark spot in the case of a = 1 (left panel) and a = 0 . 75 (right panel). The closed curve is the position of the outer boundary of the classical black hole shadow at the celestial sphere. The dashed ring is the size of the event horizon in the imaginary Euclidean space without gravity. Arrow shows the direction of the black hole spin.

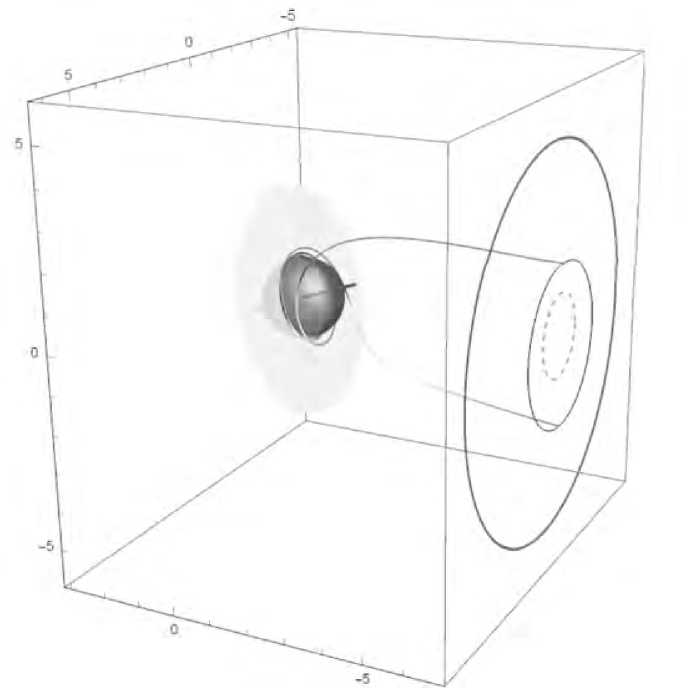
Рис. 5. Spin orientation of the supermassive black hole M87* athe center of the giant elliptical galaxy M87 with respect to the distant observer at the Earth. Arrow shows the direction of the black hole spin. The grey disk is a thin accretion disk in the equatorial plane of this black hole. The biggest closed curve at the right side of the box is a outer boundary of the projection of classical black hole shadow at the celestial sphere. The smaller closed curve is the outer boundary of the dark spot, which in this case is a gravitationally lensed equator of the event horizon globe. The inner part of the dark spot is a gravitationally lensed south hemisphere of the black hole globe. The dashed ring is the size of the event horizon in the imaginary Euclidean space without gravity. Arrow shows the direction of the black hole spin.

The very promising physical idea for the explanation of the relativistic jet formation and energy extraction from the fast-rotating black holes was formulated by the Blandford and Znajek [38]. This idea nowadays is called the “Blandford-—Znajek mechanism” and confirmed by the numerous General Relativistic Magneto-Hydro-Dynamical (GRMHD) supercomputer simulations [53, 54, 55, 56].

The crucial point of the “Blandford-—Znajek mechanism” is the electric current, generated in the accreting plasma and flowing through the event horizon of fast-rotating black hole. The accreting plasma under these conditions is continuously heated by the electric current up to the very vicinity of the black hole event horizon. Correspondingly, the heated plasma ensures the strong radiation emission from the very vicinity of the black hole event horizon. Additionally, it is generated the emission of the electromagnetic radiation in the form of the Pointing energy flux P along the black hole rotation axis: P = (1/4)c[EH] with c — velocity of light and, respectively, the electric and magnetic fields E and H, generated by the accreting plasma around the black hole.

It must be checked that in the classical Shakura-—Sunyaev alpha-model of the accretion disc [57] the strong emission of accreting plasma is absent inside the region without the stable motion due to a fast cooling-down of the accreting plasma.

All observational data and theoretical physical ideas are in accordance with the fast rotation of supermassive black holes in the “Standard Astronomical and Astrophysical Model”.

• 1.    Recovering the spins of supermassive black holes from the form of their images

The angular momenta of black holes in the General Relativity are described by the classical Kerr metric [10], depending on two parameters: the dimensional spin a, valued in the range 0 <  q < 1 and the black hole mass M (if 0 <  q < 1), or the mass of naked singularity (if q > 1).

The images (or silhouettes) of supermassive black holes M87* at the center of the giant galaxy M87 and SgrA* at the center of our Galaxy, obtained recently by the Event Horizon Telescope collaboration [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14], open the unique possibility for the recovering spin values of these black holes. In accordance with the theoretical predictions for Einstein gravity and for modified gravity theories both the form and size of the dark spots at the central parts of the observed images strongly depend on the black hole spin value.

The simplest possible image is the classical black hole shadow, which is the capture photon cross section in the strong black hole gravitational field. The corresponding equation for the outer boundary of the classical black hole shadow can be written in the following parametric form (A, q) = (X(『), q(『)), [18, 27]:

—r ³ + 3 丁 ² — q ² ( 厂 + 1)      2    r ³ [4 q ² — r[(r — 3)] ² ]

.

(1.1)

Q ( r — 1)         ， q          Q 2 (r — 1) 2

Here A and q are the orbital parameters of photon trajectories, related with the horizontal and vertical impact parameters q and 仇 respectively, for the projection of the Kerr black hole shadow on the celestial sky, viewed by a distant observer at the black hole equatorial plane [22, 23].

The very intriguing possibility for the described spin measurement is in detection of the photon ring structures just outside and inside the classical black hole shadow. This detection is a main task of the projected Millimetron Space Observatory [58, 59].

At last, the additional possibility to measure the supermassive black hole spins is related with the Lense-Thirring orbital shift of the short-period S-stars orbiting supermassive black hole Sgr A* [60] and with the observations of wobbling and rotation of relativistic jet near black hole event horizons [61, 62, 63].

At all Figures of this paper the linear unit is GM/c ² = 1, where G — Newtonian constant, M — black hole mass, c — velocity of light. Correspondingly, the projection of the classical black hole shadow on the celestial sphere is drawing by grey color. It is also sometimes shown the closed curve of the outer boundary of this classical black hole shadow. Arrow shows the direction of the black hole spin. The dashed ring is the size of the event horizon in the imaginary Euclidean space without gravity.

See in Figure 1 the examples of 3 。 numerically calculated trajectories of massive test particles, infalling into the fast rotating black hole with spin q = 1. Particles are winding on the event horizon in the direction of the black hole rotation by approaching to the black hole. The dark grey sphere is the globe of the black hole event horizon.

Figure 2 shows a reconstruction of the lensed event horizon globus of the supermassive black hole SgrA* with distant observer a little bit above the black hole equatorial plane. The closed curves are meridians and parallels on the lensed event horizon globe. The dashed curve is the null meridian. The grey region is the projection of the classical black hole shadow on the celestial sphere. For more details see [41, 42, 43, 44, 45, 46, 47, 48, 49].

Figures 3 demonstrates the numerically calculated forms of dark spots for the case of supermassive black hole SgrA* with a distant observer at the black hole equatorial plane and with the spin values q = 0 and q = 0.65, respectively. The closed curve is the position of the outer boundary of the classical black hole shadow at the celestial sphere.

Figure 4 shows the the superposition of the Event Horizon Telescope image of supermassive black hole SgrA* with the corresponding numerically modelled dark spot in the case of q = 1 (left panel) and q = 0.75 (right panel). Again, the closed curve is the position of the outer boundary of the classical black hole shadow at the celestial sphere.

superposition of the Event Horizon Telescope image of supermassive black hole SgrA* with the corresponding dark spot in the case of q = 1 (left panel) and q = 0.75 (right panel).

At last, Figure 5 demonstrates the 3D position and orientation of the supermassive black hole M87* with respect to the distant observer at the Earth.

Finally, we used the numerically calculated sizes of dark spots in the EventHorizon Telescope images of SgrA* and M87* for inferring their spins, 0.65 <  q < 0.9 and q > 0.75, respectively. For more details see [49].

Conclusion

The supermassive black holes are the important ingredients of the “Standard Astronomical and Astrophysical Model”. Nowadays all observational data and theoretical physical ideas are in accordance with the fast rotation of supermassive black holes.

The gravitationally lensed images (silhouettes) of event horizons are always pro jected at the celestial sphere inside the awaited positions of the classical black hole shadows. We used the numerically calculated sizes of dark spots in the EHT images of supermassive black holes SgrA* and M87* for inferring their spins, 0.65 <  q < 0.9 and q > 0.75, respectively.

It would be possible to reconstruct the dark spot forms at the images of supermassive black holes SgrA* and M87* with the pro jected Millimetron Space Observatory, by using the model of geometrically thin accretion disk highlighting black hole in the vicinity of its event horizon. This reconstruction also provides the possibility for spin determinations of these supermassive black holes.

Acknowledgments: I am very grateful to E. O. Babichev, V. A. Berezin, Yu. N. Eroshenko and N. O. Nazarova for stimulating discussions.