Спиральные галактические волны, генерируемые темным гало
Автор: Хоперсков Александр Валентинович, Еремин Михаил Анатольевич, Бутенко Мария Анатольевна, Храпов Сергей Сергеевич
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Астрофизика
Статья в выпуске: 11, 2007 года.
Бесплатный доступ
Построены численные модели газовых и звездных дисков в неосесимметричном внешнем гравитационном потенциале. Обсуждается возможность генерации галактических спиральных структур триаксиальным массивным темным гало.
Короткий адрес: https://sciup.org/14968597
IDR: 14968597 | УДК: 524.6
Текст научной статьи Спиральные галактические волны, генерируемые темным гало
Проблема определения механизмов генерации и поддержания спиральных галактических структур несмотря на почти столетнюю историю далека от окончательного решения. Отметим важнейший результат, связанный с работой Линдел-Белла, который предположил, что спиральный узор – есть волна. Второй результат был получен Лином и Шу [11], которые предложили математический аппарат для описания собственных мод в бесстолкновительном диске. Весь дальнейший прогресс, включая исследования гравитационной устойчивости начиная с работы Тоомре, был связан с рассмотрением прежде всего линейных волн (см. подробнее обзор Паши [12]). Нелинейный анализ, основанный на аналитических подходах, имел ограниченное применение, заведомо ограничиваясь стационарными волнами в однородном бесконечно тонком диске.
По морфологии традиционно выделяют два основных типа спиралей: глобальный спиральный узор (grand design) и флокулентные спирали. В первом случае считается, что в диске имеется стационарная твердотельно вращающаяся волна плотности в звездно-газовом диске. Второй принято объяснять индуцированным звездообразованием, но, по-видимому, между этими двумя классами объектов нет четкой границы. В классических галактиках с глобальным спиральным узором можно обнаружить различные признаки действия второго механизма (ветвления спиралей; неоднородность звездообразования и распределения газовых комплексов и облаков вдоль спирального рукава; локальные вспышки звездообразования вне основного спирального узора). С другой стороны, у галактик второго типа можно обнаружить достаточно правильные спиральные рукава заметной амплитуды в полосах I , R , K , что свидетельствует о волне плотности в старом звездном диске.
Условия для генерации и поддержания спирального узора заметно улучшаются при наличии газовой подсистемы – чем она массивнее и чем эффективнее газ охлаждается, тем более долгоживущей оказывается спиральная структура. Однако и в этом случае не удается объяснить данные наблюдений. Звездный диск быстро разогревается и оказывается гравитационно устойчивым, несмотря на появление холодной подсистемы молодых звезд в результате звездообразования. Кроме того, последний процесс приводит к уменьшению массы газовой компоненты, что также негативно влияет на условия существования волн плотности.
С другой стороны, при наличии внешнего воздействия из-за массивных спутников спиральные структуры легко рождаются как в моделях N -тел, так и в наблюдаемых галактиках, где часто прослеживается приливное взаимодействие [1].
Важнейшим результатом физики галактик является осознание того факта, что внутри оптического радиуса R (примерно в пределах сферы, где располагается звездный диск) на долю темного гало приходится половина и больше гравитирующей массы. И ситуация, когда барионное вещество внутри R доминирует встречается в мире изолированных (слабовзаимодействующих) дисковых галактик реже, чаще доминирует темное гало. Построить сколько-нибудь реалистичную модель дисковой галактики, согласующуюся с данными наблюдений, без учета достаточно массивного гало не удается [3–5].
Для простоты гало принято считать центрально симметричным. Однако указания на отсутствие центральной симметрии (в частности, осевой симметрии) из наблюдений появились достаточно давно, но они не выглядели достаточно надежными. В последние годы на триаксиальность гало указывают самые различные данные наблюдений [6–10; 15].
В данной работе рассмотрим динамику дисков в неосесимметричном гало.
Динамические модели дисков в триаксиальном гало
Моделью звездного диска является система N -гравитационно взаимодействующих частиц, образующих экспоненциальный диск с радиальной шкалой L a и вертикальной А , которая описывается системой дифференциальных уравнений:
d2 П ( t ) dt 2
N — —
= У f + ij bu lge
*
+ fhallo
j = 1 i * j
где f j ( Г - r j ) - удельная сила взаимодействия i -й частицы с j -й;
f u 18 e - определяет наличие балджа, а сила f .^ обусловлена триаксиальным гало.
В модели N -тел самогравитация рассчитывается на основе алгоритма TREEcode. Динамическая модель подробно описана в работах [3; 4].
Эволюция газовой компоненты определяется системой уравнений гидродинамики во внешнем гравитационном поле звездного диска и триаксиального гало. Начальные распределения параметров определяются радиальным балансом
V _ d ф о _ dp о = о r dr о 0 dr ,
где V ϕ – скорость вращения;
p 0 , σ 0 и Ф 0 – равновесные поверхностные давление, плотность газа и общий потенциал, соответственно;
и вертикальным балансом – уравнением гидростатического равновесия:
dPd
=-’ dzdz с учетом уравнения состояния, которое связывает давление P, энергию E и объемную плотность ρ: P = (ρ, E). В качестве методов численного интегрирования использовались TVD- и SPH-подходы [2; 13].
Характер распределения массы в темном гало из наблюдений определяется крайне неуверенно. Выберем в качестве базовой модели обобщение квазиизотермического гало, для которого выражение силы faOo = { F x , F y , F z } имеет вид:
F x = F ( 5 ) ^, F y = F ( 5 ) ^У г, F z = F ( 5 ) z . (4)
Величина
F ( 5 ) = - 4 n G p o a 2 1 5 - arctg ( 5 ) | (5)
зависит только от комбинации 5 = J x 2 / c 2 + y 2 / b 2 + z 2 / a 2 , p 0 — центральная объемная плотность, c , b , a – шкалы гало в трех перпендикулярных направлениях. В пределе a = b = c имеем центрально-симметричное гало, а параметры q = a / b и s = b / c определяют степень триаксиальности гало. Уравнение Пуассона для гравитационного потенциала позволяет определить соответствующее распределение плотности в гало ρh ( x , y , z ).
Рассмотрим внешний потенциал гало в отличном от (5) виде
Ф tot =Ф o ( г ) + Ф 1 ( г , Ф, t ), (6)
где r = ^x2 + y 2 + z 2 - сферическая радиальная координата;
Ф0 – осесимметричная часть потенциала, представляющая собой потенциал квазиизотермического гало в случае a = b = c [см. (5)].
Неосесимметричное возмущение можно выбрать в форме
Ф 1 = Ф о ( r)6 o ( Г , t ) cos(2( ф -Q h t )). (7)
Для безразмерной амплитуды г (r, t) в условиях стационарного состояния можно записать z х (r / d )2
' r ) = 6 0 [1 + ( - / d ) 2 ] 3' 2 ' (8)
здесь d – характерный масштаб;
ε 0 – определяет степень неосесимметричности и вводится в расчет подобно параметру q для неосесимметричного гало.
Г ало вращается с угловой скоростью Q h , которая меньше угловой скорости вращения диска на периферии Q ( R ) = V ( R ) / R . Если типичные значения линейной скорости V ( R ) для галактических дисков лежат в пределах ~100 ^ 300 км/с ( Q ( R ) ~ 10 ^ 30 км/с/кпк), то для угловой скорости гало следует Q h < 5 км/с/кпк в соответствии с кинематикой эллиптических галактик.
В качестве начального распределения массы гало выбиралось центрально-симметричное, затем в течение характерного времени τh переходили от центрально-симметричного гало к триаксиальному.
В рамках N-тел и газодинамических самосогласованных моделей рассмотрим принципиальный вопрос о возможности генерации спиральной структуры в триаксиальном гало, не противоречащем данным наблюдений. В первом приближении гало характеризуется значением степени неосесимметричности в плоскости диска, которое допускает описание квази-эллипсоидальных систем, по своим параметрам соответствующих эллиптическим галактикам от E0 до E7.
Результаты моделирования свелись к следующему. С использованием моделей N -тел продемонстрирована возможность формирования в самогравитирующем звездном диске спиральных волновых структур из-за наличия неосесимметричного гало (рис. 1). Обнаружен квазипери-одический режим параметров спиральной структуры. Амплитуда волны на заданном радиусе изменяется квазипериодически с характерным периодом, зависящим от угловой скорости вращения гало при прочих равных условиях в дисковой подсистеме. Временные зависимости основных макроскопических параметров (плотности, скорости, дисперсий скоростей) в плоскости диска, а также Фурье-гармоник возмущений, демонстрируют формирование глобального спирального узора. Показано, что разогрев диска незначителен – за 10 оборотов вращения периферии диска дисперсия скоростей монотонно увеличивается в пределах 10–15 %. При этом отношение дисперсии вертикальных скоростей к дисперсии радиальных скоростей сохраняется неизменным в пределах 3 %. Сравнение вертикальных профилей диска в осесимметричном диске и при наличии спиральных структур из-за триаксиальности гало указывает на возможность дополнительного увеличения характерной вертикальной шкалы диска в моделях с неосесимметричным гало, что представляется актуальным для анализа галактик, видимых с ребра (edge-on).
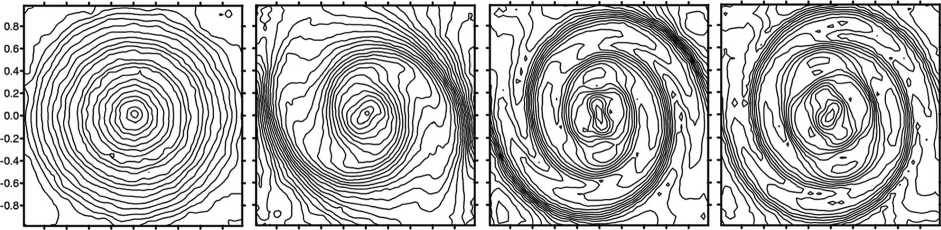
0,8 -0.6 -0.4 -0,2 0,0 0,2 0,4 0,6 0.8 -0.8 -0.6 -0.4 -0.2 0.0 0.2 0.4 0.6 0.8 -0.8 -0.6 -0.4 -0.2 0.0 0.2 0.4 0.6 0.8 -0.8 -0.6 -0.4 -0.2 0.0 0.2 0.4 0.6 0.8
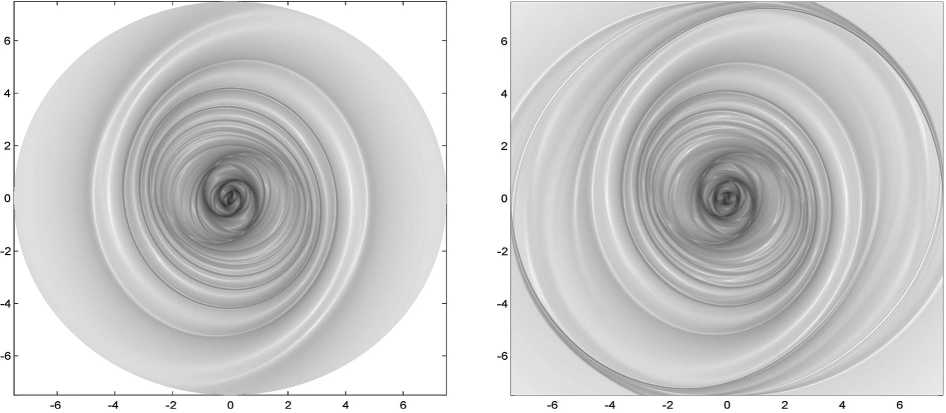
Рис. 1. Изолинии логарифма поверхностной плотности бесстолкновительного звездного амогравитирующего диска в гравитационном поле неосесимметричного массивного темного гало в разные моменты времени. Спиральная структура быстро формируется в диске, который первоначально являлся осесимметричным. При тех же самых условиях в случае центральносимметричного гало диск остается осесимметричным на протяжении десятков периодов обращения внешнего края дисковой компоненты (порядка 10 млрд лет)
Гидродинамические расчеты эволюции газовых дисков в триаксиальном гало свидетельствуют о принципиальной возможности формирования спиральной структуры в газовом диске из-за неосесимметричности массивного темного гало (рис. 2).
Вычисление дивергенции скорости в плоскости диска показывает, что образуется система сильных ударных волн (рис. 3). Нелинейные (ударные) волны имеют крупномасштабную структуру, захватывая диск вплоть до малых значений плотности ρ / ρ max ~ 10 –3 . Форма спирали rl ( ϕ ) существенно зависит от параметров модели, но угол, на который поворачивается фронт волны, превышает значение 2 π и может достигать 4 π (см. рис. 4).
Полученные результаты не зависят от наличия внешней границы диска в численной модели TVD на r = R out. . Граница звездного диска простирается до R st ar = 1,25 = 5 L a. Для этого необходимо в случае сеточных методов (TVD) переносить внешнюю границу далеко за пределы области, которая представляет интерес для моделирования. Тестовые расчеты показали, что только начиная с R out > 10 R star граница заведомо не оказывает влияния на эволюцию иска. В данной работе результаты приведены для Rout = 12 Rstar = 15, что требует большого числа ячеек в радиальном направлении Nr > 1500. В азимутальном направлении N ^ = 180 ^ 360. В случае SPH-модели указанная проблема границы отсутствует.
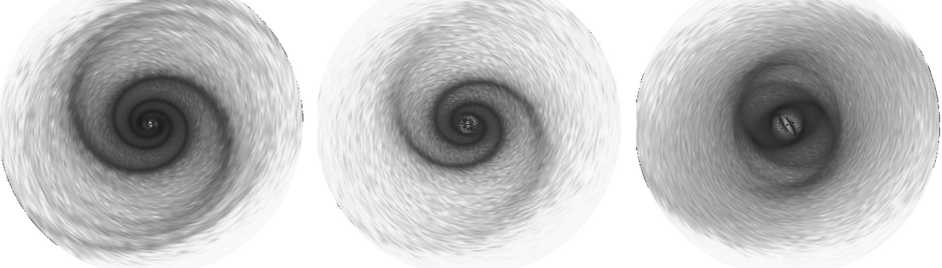
Спиральная структура существенно зависит от угловой скорости вращения и степени триаксиальности гало. Важным параметром является также число Маха M = V / cs . На рисунке 4 показана структура возмущений в модели SPH при различных начальных значениях M . Температуру диска удобно характеризовать параметром A p = c s2 ( r = 0) / у , где c s -адиабатическая скорость звука. Чем больше число Маха (случай Ap = 0,005 на рис. 4), тем более благоприятными являются условия для генерации спиральной структуры. В более горячем диске ( Ap = 0,06) спиральный узор оказывается слабым.
Влияние границ в численной модели газового диска
Обсудим подробнее наличие границ в численной модели при использовании эйлеровых сеток.
-
1) В случае цилиндрической системы координат { r i ,
j } ( i = 1, N ; j = 1, M ) особой точкой является r = 0, что приводит к необходимости задания граничных условий на окружности r 1 .
-
2) Аналогичная проблема возникает на внешней радиальной границе rN .
Выше было указано, что несмотря на то, что плотность вещества на больших расстояниях от центра убывает, внешнюю границу rM приходится задавать в области, где отношение плотностей r ( р М ) / r ( p 1 ) < 10 -8 , что соответствует 10 радиусам звездного диска. Таким образом, большая часть расчетной области используется неэффективно.
Рассмотрим внутреннюю границу. В декартовой системе координат ( x , y ) в центре диска особенность отсутствует, поэтому сравним результаты расчетов в цилиндрической и декартовой системах координат (см. рис. 5). Как видим, при прочих равных условиях эволюция дисков имеет сходный характер.
Чтобы полностью избавиться от влияния внешней границы была построена численная модель в цилиндрической системе координат с диском конечного радиуса, у которого внутри расчетной области имеется граница вещество – вакуум. Модель основана на регуляризации физических величин [2]. Во-первых, на шагах «предиктор» и «корректор» зануляются значения в ячейках, плотность в которых меньше некоторого предела, в частности, в качестве критического значения плотности выбиралось 10 –8 . Во-вторых, при вычислении потоков через границы ячеек необходимо учитывать наличие ячеек, граничащих с вакуумом, и в этом случае явно переключаться на волну разрежения, коррекно вычисляя границы скоростей возмущений внутри ячейки.
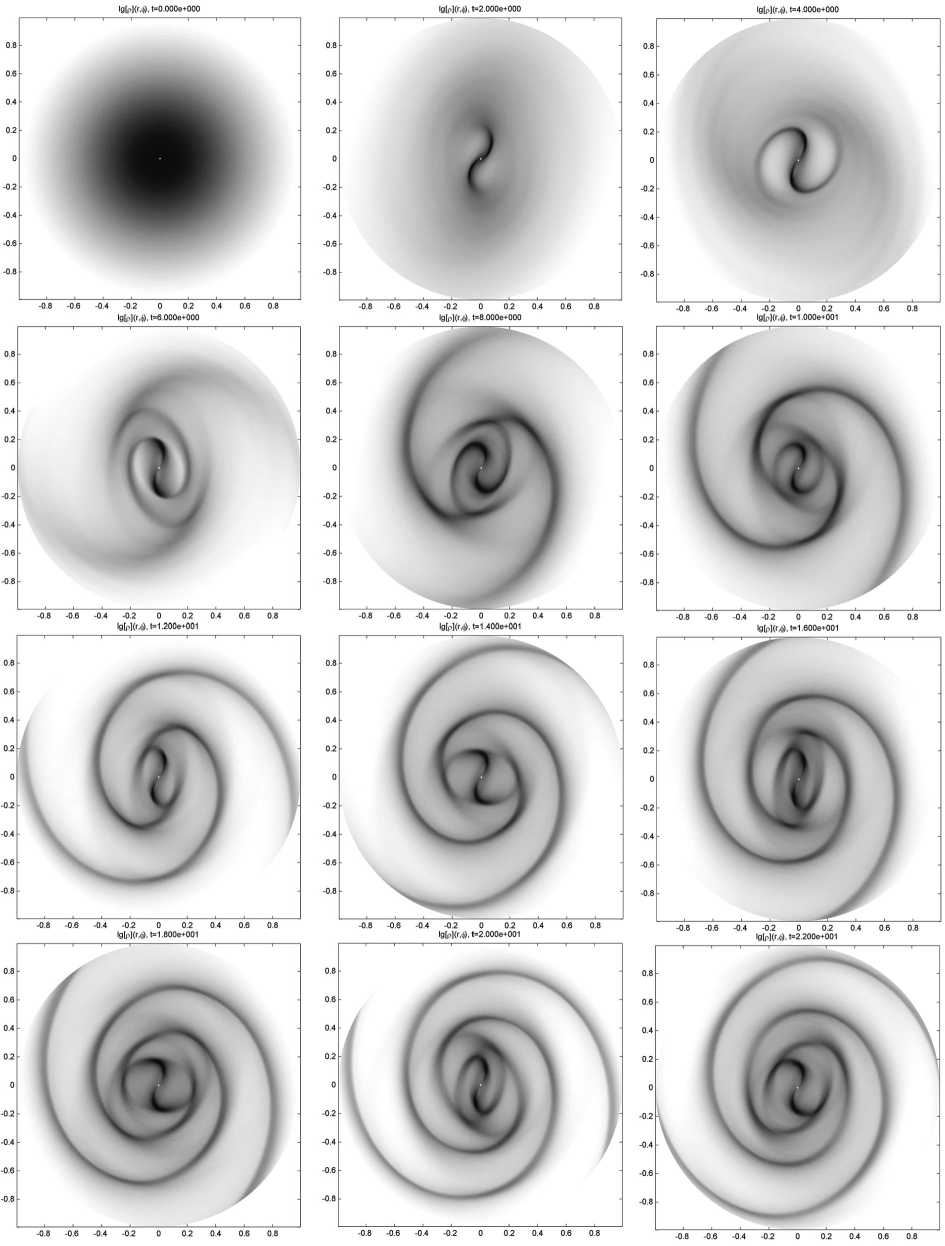
1дЫ(М), t=1 .ОООе+001
1д[р](г,ф», t=0.000e+000
-0.8 -0.6 -0.4 -0.2 О 0.2 0.4 0.6 0.8
1д[р](г,ф), t=6.000e+000
-0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8
lg[p](r,4), t=1.200е+001
-0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8
IgfplM, t=1.800e+001
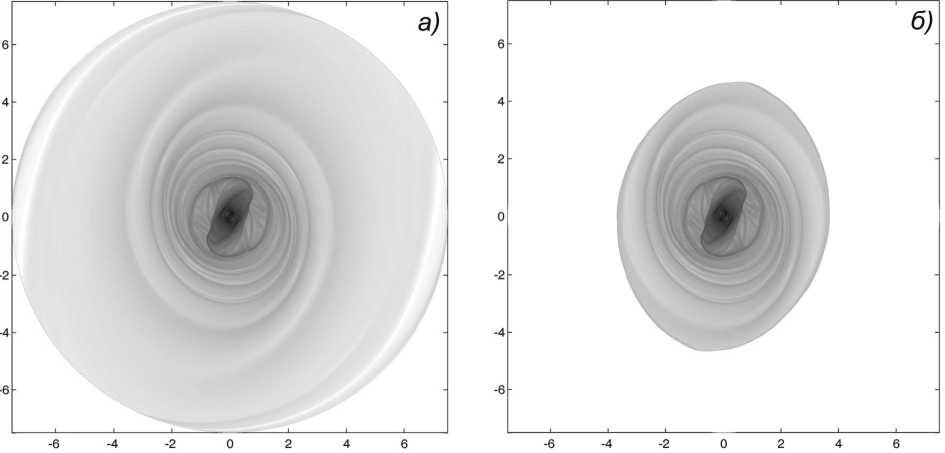
lg[p](r. -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1д[р](г,ф), t=8.000e+000 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 lg[p](r,«),t=1.400e+001 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1д[р](г,ф), t=2.000e+001 lg[p](r.4). t=4.000e+000 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1д[рКг,У, t=1.600e+001 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1д[р1(г,ф), t=2.200e+001 Рис. 2. Распределение логарифма поверхностной плотности газа в центральной области звездно-газового диска в различные моменты времени при наличии неосесимметричного потенциала. Диск вращается против часовой стрелки. Период полного оборота диска на радиусе равен r = 1 равен t ≈ 3 Рис. 3. Изолинии логарифма плотности газового диска (TVD) в триаксиальном гало на существенно нелинейной стадии эволюции волн (слева). Распределение логарифма квадрата дивергенции скорости (справа) наглядно показывает наличие мощных ударных волн в диске и их местоположение в центральной области диска r ≤ 1,5 (тонкие спирали с резким градиентом цвета на изображении) Рис. 4. Структура волн при различных значениях параметра Ap = 0,005; 0,015; 0,06 Все эти процедуры приводят к появлению радиальной скорости у вещества в «обрезаемых» ячейках и разрушению первоначального равновесия, но, как показали расчеты, это совершенно не влияет на результаты моделирования, если внутри расчетной области процессы нестационарны. На рисунке 6 продемонстрировано отсутствие каких-либо существенных различий между результатами расчетов без регуляризации, когда вещество простирается до расчетной границы, и с регуляризацией – во внешней части диска имеем границу газ – вакуум. В последнем случае вещество не доходит до внешнего радиуса сетки rN, тем самым граница совершенно не оказывает влияния на динамику газа. Рис. 5. Сравнения расчетов в различных системах координат – полярной (слева) и декартовой (справа). Разрешение Ar =Ax = Ay = 0,01, Аф= 1°. В полярной системе координат [0; 7,5] х [0; 180], сетка 750 х 180, в декартовой [- 7,5; 7,5] х [- 7,5; 7,5], сетка 1500 х 1500. Граничные условия одинаковые – фиксированный градиент величин на входных границах Рис. 6. Распределения поверхностной плотности в моделях без регуляризации (а) и с регуляризацией (б). Все параметры одинаковы: 0,01 х 1°, постоянная адиабатичности Ap = 0,02, показатель адиабаты у = 1,1. Начальное распределение плотности в плоскости диска p(r, t = 0) =1/(1 + (rIa 1)2 + (rIa2)6), a 1 = 0,5, a2 = 0,25, что обеспечивает быстрый спад плотности с ростом r Основные результаты 1. Триаксиальное гало может являться эффективным генератором долгоживущей спиральной структуры в звездно-газовом диске. 2. Формирующийся спиральный узор во внешней части диска является двухрукавным, а спирали отстающие. 3. Имеется качественное согласие результатов расчетов в различных моделях звездных, газовых, звездно-газовых дисков. Были рассмотрены модели с учетом и без учета самогравитации (для газовой компоненты), для различных законов распределения темной массы в гало. В широких пределах варьировались: показатель адиабаты газа, начальные радиальные профили плотности звездной и газовой компонент, дисперсии скоростей звездного диска и скорости звука газа. Характер распределения начальных квазиравновесных параметров газа и звезд в дисковых компонентах практически не влияет на формирующийся спиральный узор, если начальное состояние гравитационно устойчиво. 4. В газовом диске образуются ударные волны, локализация которых не связана с потенциальной ямой от неосесимметричного массивного гало. Формирование ударных волн во вращающемся газе, который находится в глобальном неосесимметричном потенциале, отличается от случая одномерного протекания газа сквозь потенциальную яму. 5. Нелинейные спиральные волны в газовом диске образуются при малой неосесиммет-рии гало, начиная с отношения полуосей е0 = (b - c) / b > 0,02. В звездном диске без газа амплитуда возмущений нарастает до заметных значений, если £0 > 0,05. Наличие самогравитирующего газа улучшает условия для генерации спирального узора в бесстолкновительной звездной компоненте. 6. Рассмотренные две модели неосесимметричного гало, различающиеся характером распределения плотности темного вещества, приводят к спиральным узорам, которые могут отличаться геометрией. 7. Проведено последовательное сравнение динамики спиральных структур в рамках различных численных методов решения уравнений гидродинамики: на эйлеровых сетках в цилиндрической и декартовой системах координат и в случае лагранжевого подхода. Реализована численная модель, включающая расчет границы вещество – вакуум внутри области моделирования. Показано согласие результатов расчетов при использовании указанных различных методов моделирования.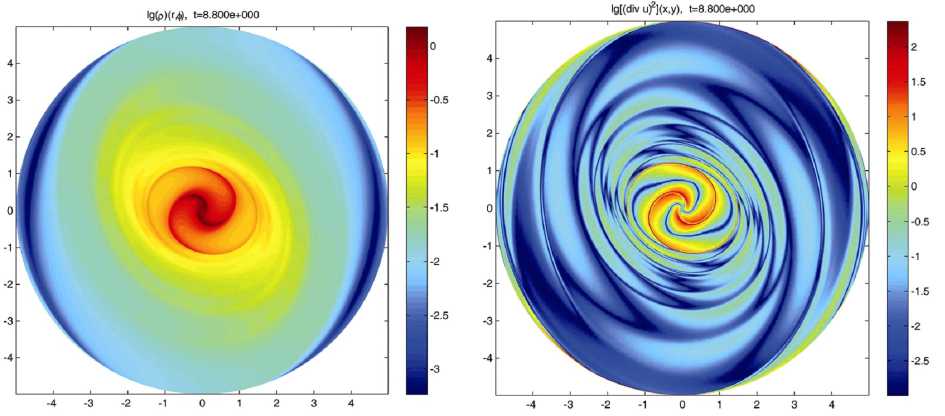
Список литературы Спиральные галактические волны, генерируемые темным гало
- Ефремов Ю.Н., Корчагин В.И., Марочник Л.С., Сучков А.А. Современные представления о природе спиральной структуры галактик//УФН. 1989. Т. 157. С. 599.
- Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений. М.: Физматлит, 2001. 608 с.
- Хоперсков А.В., Засов А.В., Тюрина Н.В. Оценка масс сферических и дисковых компонент галактике использованием численного моделирования//Астрон. журн. 2001. Т. 78. С. 213.
- Хоперсков А.В., Засов А.В., Тюрина Н.В. Минимальная дисперсия скоростей в устойчивых звездных дисках. Численные эксперименты//Астрон. журн. 2003. Т. 80. С. 387.
- Засов А.В., Хоперсюв А.В., Тюрина Н.В. Дисперсия скоростей звезд и оценка массы галактических дисков//Письма в Астрон. журн. 2004. Т. 30. С. 653.
- Helmi A. Is the dark halo of our Galaxy spherical?//Monthly Not. R. Astron. Soc. 2004. V. 351. P. 643.
- Gnedin O.Y., Gould A., Miralda-Escude J., Zentner A.R. Probing the Shape of the Galactic Halo with Hypervelocity Stars//Astron. J. 2005. V. 634. P. 344.
- Johnston K.V., Law D.R., Majewski S.R. A Two Micron All Sky Survey View of the Sagittarius Dwarf Galaxy. III. Constraints on the Flattening of the Galactic Halo//Astron. J. 2005. V. 619. P. 800.
- Keller S.C., Murphy S., Prior S., DaCosta G., Schmidt B. Revealing Substructure in the Galactic Halo The SEKBORRLyrae Survey//Astron. J. 2008. V. 678. P. 851.
- Kuhlen M., Diemand J., Madau P. The Shapes, Orientation, and Alignment of Galactic Dark Matter Subhalos//Astron. J. 2007. V 671. P. 1135.
- Lin С.C., Shu F.H. On the spiral structure of disk galaxies//Astron. J. 1964. V. 140.P646.
- Pasha I.I. Density-wave spiral \ theories in the 1960s. I. II//Astro-ph/0406142, astro-ph/0406143.
- Price D.J. Magnetic fields in Astrophysics//Ph.D. thesis, Institute of Astronomy & Churchill College University of Cambridge, 2004.
- Tutukov A.V., Fedorova A. The role of close passages of galaxies and the asymmetry of their dark haloes in the formation of their spiral patterns//Astr. Rep. 2006. V. 50. P. 785.
- Zentner et al. The anisotropic distribution of galactic satellites//Astron. J. 2005. V. 629. P. 219.


