Спиральные пучки света - новое направление когерентной оптики

Как известно, распространение светового поля, в частности лазерного пучка, представляет собой волновое явление и, как всякий колебательный процесс, характеризуется распределением амплитуды и фазы.

Если распределения амплитуды и фазы поля заданы в некоторой плоскости, то последующая эволюция поля при распространении описывается тем или иным дифференциальным уравнением. Отсюда следует, что световое поле при распространении, вообще говоря, претерпевает количественные и качественные изменения [1].

Однако, с открытием лазеров и появлением когерентной оптики, описывающей распространение лазерных пучков, было теоретически и экспериментально показано, что лазер может излучать световые пучки, которые самосогласованы таким образом, что сохраняют свою структуру при распространении и фокусировке с точностью до масштаба [2]. Такие пучки являются собственными колебаниями лазерных резонаторов (или модами), имеют жестко заданную форму и описываются двумя семействами специальных функций с различными типами симметрии: пучки Эрмита-Гаусса и Лагерра-Гаусса, при этом низший тип колебаний в этих семействах совпадает и является известной двумерной функцией Гаусса. На рис.1 приведены примеры поперечных распределений интенсивности высших типов пучков [3]. Структура этих пучков сохраняется при распространении и фокусировке и может ассоциироваться с однородными деформациями растя жения-сжатия: сходящиеся и расходящиеся пучки. Закономерно поставить вопрос: имеется ли некая оптическая аналогия деформации кручения для пучков с неоднородной расходимостью? Как показано в [4], поток световой энергии состоит в общем случае из двух компонент: потенциальной и вихревой. В определенном смысле, первая компонента соответствует деформациям растяжения-сжатия, а вторая - деформациям кручения.

Принимая во внимание вихревую компоненту потока световой энергии, можно расширить понятие структурной устойчивости световых полей, а именно, поставить следующую задачу: существуют ли лазерные пучки, сохраняющие свою структуру при распространении и фокусировке с точностью до масштаба и вращения?

Спиральные пучки света

В работе [7] найден и полностью описан новый класс лазерных пучков, названных спиральными, которые сохраняют свою

Рис.1. Примеры распределений интенсивности пучка Эрмита-Гаусса (а) и пучка Лагерра-Гаусса (b)

структуру при распространении и фокусировке и могут иметь различные параметры вращения.

Известные упомянутые выше типы лазерных мод Эрмита-Гаусса и Лагерра-Гаусса являются частными случаями спиральных пучков с нулевым вращением. Отличие найденных пучков от известных в том, что они обладают двумя принципиально новыми свойствами.

Во-первых, сохраняя форму при распространении и фокусировке, они могут иметь весьма разнообразную структуру распределения интенсивности. В частности, в семействе спиральных пучков теоретически найдены и на отдельных примерах реализованы экспериментально спиральные пучки в форме произвольных кривых или их совокупности [10]. Комплексная амплитуда найденных пучков в виде кривой, заданной в комплексной параметрической форме z=z( t )= x ( t )+i y(t ), t О[0, T ], определяется выражением

S ( z , z Z ( t ), t e[0, T ] ) =

• Z^ ₊ 2^ t ) ₊      -

• , P r                 Z'(t)dt.

• —] ( z ( t ) Z '( t ) - z ( t ) Z '( t ) ) dt

P 0                          J

-

I zz ]_f

= ^ep  p j>:

+

Здесь r - гауссов параметр. Кривая z ( t ) названа порождающей для спирального пучка (1). Примеры пучков, построенных по формуле (1), приведены на рис.2.

Отметим еще раз, что в отличие от световых полей с заданным распределением интенсивности, формируемых ранее известными методами, эти спиральные пучки сохраняют свою структуру в любой плоскости наблюдения и фокусировки. Таким образом, данное свойство спиральных пучков позволяет весьма гибко менять их форму при сохранении структурной устойчивости, что представляет существенный интерес для лазерной медицины и технологии.

Во-вторых, вихревой характер распространения световой энергии в пучках обуславливает то, что пучки обладают существенно ненулевым угловым моментом количества движения [8]. Это проявляется в том, что микроскопические объекты размерами в десятки микрон (например, живые клетки), помещенные в область фокусировки такого пучка могут приводиться во вращение вокруг своего центра инерции, удерживаться в заданной области пространства, подвергаться неоднородным заданным деформациям и т.п.

Эти два свойства дают возможность создания в области фокусировки заданных микрораспределений интенсивности и углового

Рис.2. Примеры спиральных пучков в виде кривых: треугольник, квадрат и спираль Архимеда (интенсивности - верхний ряд, фазы - нижний ряд). Белый цвет соответствует фазе 2p, черный - нулевой. Концевые точки изофазных линий показывают местоположение изолированных нулей интенсивности, называемых также оптическими вихрями

момента, что представляет принципиально новый инструмент для бесконтактного манипулирования микрообъектами в электронике и микробиологии [5].

При исследовании свойств спиральных пучков для замкнутых порождающих кривых было установлено, что такие пучки проявляют характерные свойства квантования: во-первых, распределение интенсивности таких пучков претерпевает радикальное изменение при преобразовании подобия кривой z ( t ) ® nz ( t ) и обладает формой кривой лишь при определенных дискретных значениях nn ; во-вторых, для этих же дискретных значений nn распределения интенсивности пучков для кривых nz ( t + a ) при различных а одинаковы; в-третьих, площадь S под кривой z ( t ) связана с гауссовым параметром r такого пучка соотношением:

S == 1 pr ² n , где N = 1,2,....... (2)

Пучки, порождающие кривые которых удовлетворяют равенству (2), названы N- квантованными.

Следует кратко отметить и квантово-механический аспект полученных результатов. Он обусловлен тем, что эволюция лазерных пучков при распространении описывается параболическим дифференциальным уравнением, полностью аналогичным уравнению Шредингера, описывающим эволюцию волновых функций квантовых систем во времени. При этом структурно устойчивым лазерным пучкам соответствуют в квантовой механике стационарные решения уравнения Шредингера с некоторым гамильтонианом. В работе [10] показано, что найденным спиральным пучкам соответствуют специфические стационарные состояния квантовой частицы в однородном магнитном поле, причем для квантово-механической аналогии - состояний заряженной частицы в однородном магнитном поле - условие (2) соответствует квантованному магнитному потоку через контур z ( t ): F= (2 p h c / | e | ) N . Данная аналогия представляет интерес в приложениях к теории квантового эффекта Холла [6].

Результаты экспериментов

Эспериментальная реализация спиральных пучков осуществлялась различными ме-

Рис.3. Экспериментальное распределение интенсивности спирального пучка в форме границы треугольника (см. теоретическое распределение на рис. 2)

тодами. Во-первых, непосредственно с помощью амплитудно-фазовых масок. Амплитудная маска и фотошаблон для фазовой маски изготавливались на фотоплоттере (разрешение 1024 x 1024, размер 10 x 10 мм²). Фотошаблон использовался для изготовления фазового элемента на дихромированной желатине. Комбинация амплитудной и фазовой масок давала требуемый амплитудно-фазовый элемент, который освещался пучком гелий-неонового лазера. Пример экспериментальной реализации пучка в виде границы треугольника показан на рис.3. Пучок сохранял свою структуру при фокусировке и поворачивался на 90 ° при распространении из области перетяжки в дальнюю зону.

Другой, менее очевидный метод синтеза таких пучков основан на результатах работы [9], где, в частности, показано, что астигматическим воздействием можно осуществить преобразование пучков Лагерра - Га-усса в пучки Эрмита - Гаусса и наоборот. Это преобразование может быть обобщено следующим образом (см. [10]):

JJ expl - i(xX + y h) + ^ixh |S(X + i h, X - i hz№dh= l

R2 __2              2_ 2 2

pr I ir xy r x I

=-^-expl -     -----Ih( ryz )

V2 (    48 J где h(rУ |z)=

I r y If - ^eX P | ^- о    I J ^eX P

= l ⁸ 0 0

' - z2M - zMO)+yz (t)+ r2

+Л J (zz'- zz ')dt r0

1 z '( t )l dt

Таким образом, задача формирования спирального пучка посредством астигматических преобразований сводится к синтезу одномерного по структуре поля h ( r y | z ) . На рис.4 показано одномерное поле h ( r y | z ) для кривой в виде границы треугольника и схема синтеза соответствующего спирального пучка. Одномерная структура поля позволяет в полной мере использовать возможности микролитографии, поэтому данный способ может быть технологически более предпочтителен, чем прямой метод амплитудно-фазовой маски.

С помощью предложенного метода были экспериментально реализованы пучки различного вида, сохраняющие свою структуру при распространении и фокусировке. На рис.5 показана экспериментальная реализация спирального пучка в виде регулярной решетки нулей, когда в качестве одномерной структуры была использована фазовая мультиплицирующая дифракционная решетка Даммана. Волновые поля такого вида (т.н. решетки вихрей) естественным образом возникают в квантово-механических задачах, связанных со сверхпроводимостью, сверхтекучестью, квантовым эффектом Холла [12].

Исследования спиральных пучков показали, что они являются собственными колебаниями специфических резонаторов с вращением поля. Был реализован аргоновый лазер с таким резонатором и впервые полу-

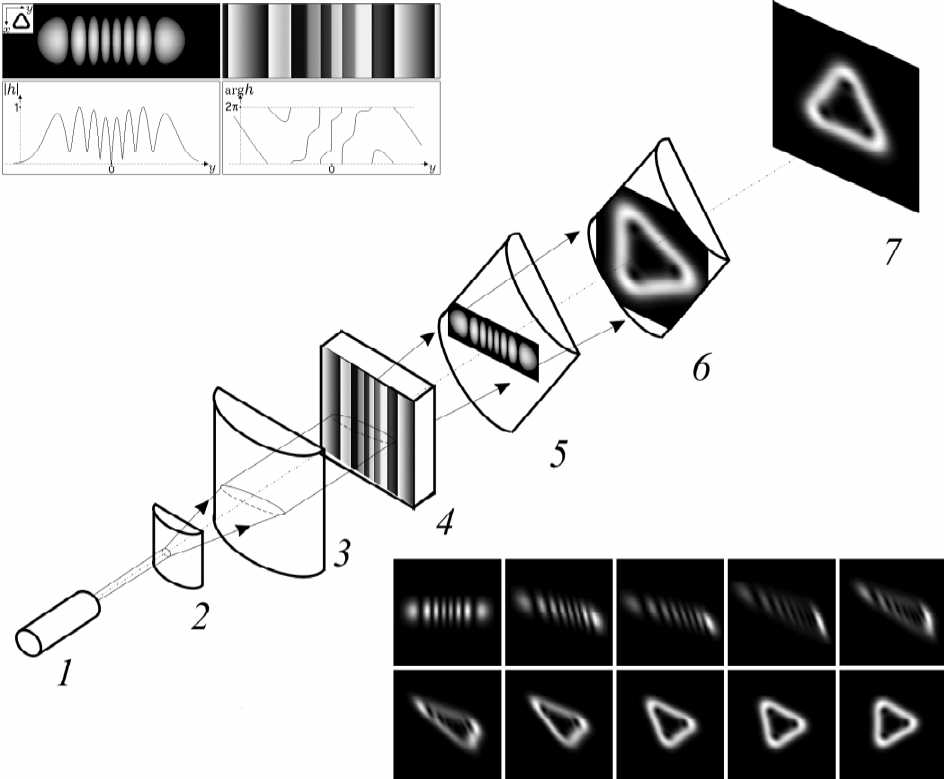
Рис.4. Оптическая схема синтеза спиральных пучков посредством одномерных по структуре оптических элементов (1 - лазер, 2,3,5,6 - цилиндрические линзы, 4 - одномерный оптический элемент, 7 - экран). В верхней части рисунка показана структура амплитудно-фазового элемента для спирального пучка в форме границы треугольника. Полутоновые изображения представляют собой амплитуду и фазу распределения exp(-r2'x2/8)h(ry\z); графики соответствуют амплитуде и фазе одномерных распределений h(iy\z). В нижней части рисунка показана динамика изменения светового поля в промежутке между линзами 5,6. За линзой 6

пучок сохраняет свою структуру и вращается при распространении

чены экспериментально спиральные пучки с различными параметрами вращения [11]. Это показывает принципиальную возможность создания лазеров, непосредственным результатом генерации которых без дополнительной нестандартной оптики будут пучки с заданными свойствами.

Использование фазовой структуры спиральных пучков с заданным распределением интенсивности как базовой дает новый подход и к известной задаче синтеза чисто фазовых элементов для фокусировки в кривые [13]. Обычно базовые решения ищутся на основе метода стационарной фазы. Можно показать (см., например, [7]), что решения на базе спиральных пучков невозможно получить таким образом. Пример решения задачи с использованием структуры спиральных пучков показан на рис.6 (амплитудная маска для фазового элемента изготовлена на фотоплоттере в Институте систем обработки изображений РАН, фазовый элемент на желатине сделан Н.Н.Лосевским). Характерной чертой получаемых решений является их однотипный топологический характер и наличие существенного количества фазовых сингулярностей (оптических вихрей), что указывает на их родство со спиральными пучками (ср., например, рис.6а и соответствующее фазовое распределение на рис.2).

Таким образом, создана теоретическая и экспериментальная основа принципиально новых возможностей целенаправленного “конструирования” лазерного излучения. На

a                    b

Рис. 5. Экспериментальная реализация спирального пучка в форме решетки нулей: интенсивность (а) и результат интерференции между спиральным и опорным пучками (b)

рис.7 представлены примеры спиральных пучков сложной формы, которые, несмотря на свой «рукотворный» вид, являются такими же естественными физико-математическими объектами как и обычные лазерные пучки, являются точными решениями уравнения Шредингера, могут быть собственными колебаниями соответствующих лазерных резонаторов и сохраняют свою структуру при распространении и фокусировке.

Заключение

Основными результатами проведенного исследования являются следующие:

• Найдены новые лазерные пучки, названные спиральными, которые сохраняют структуру своей интенсивности при распространении и фокусировке с точностью до масштаба и вращения. Показано, что данные пучки могут быть модами специфических резо-

a

b

c

Рис. 6. Фазовый элемент для фокусировки пучка с равномерной засветкой круговой апертуры в границу квадрата (а), теоретическое (b) и экспериментальное (с) распределения интенсивности в фокусе. Некоторое различие между теорией и экспериментом обусловлено погрешностями передачи контраста амплитудной маски и нелинейностями при формировании фазового рельефа слоем желатины

Рис. 7. Спиральные пучки сложной структуры (интенсивности и фазы)

наторов с вращением поля. Экспериментально реализован лазер с таким резонатором и получены пучки с различными параметрами вращения при распространении. Выявлено соответствие спиральных пучков волновым функциям заряженной частицы в однородном магнитном поле.

• •    Теоретически обоснована и экспериментально показана возможность синтеза световых полей с заданными пространственными характеристиками и сохраняющих свою структуру при распространении и фокусировке. Найден класс лазерных пучков, распределение интенсивности которых имеет форму произвольной плоской линии. Разработаны основы оптики таких пучков.

• •    На основе полученных закономерностей преобразования пучков Лагерра-Гаусса в пучки Эрмита-Гаусса разработан метод синтеза спиральных пучков посредством одномерных амплитудно-фазовых элементов.

Данная работа частично поддержана Российским фондом фундаментальных исследований (грант 99-02-16513).