Сплавы с памятью формы: применение в медицине. Обзор моделей, описывающих их поведение

Большой интерес исследователей вызывает соединение титана с никелем – никелид титана, или нитинол, у которого наряду с пластичностью обнаружено уникальное свойство, получившее название «эффекта памяти формы». Открытому в 50-е годы прошлого столетия в США в Военно-морской лаборатории эффекту памяти формы нашлось практическое применение.

Эффект заключается в способности ненагруженного материала под воздействием внешнего напряжения и изменения температуры накапливать деформацию (10–15%), обратимую либо при нагреве, либо в процессе снятия внешнего напряжения (сверхэластичность). Деформация может накапливаться при активном нагружении, а также при изменении температуры сплава, находящегося под воздействием одноосного или сдвигового напряжения. Типичный рабочий цикл для

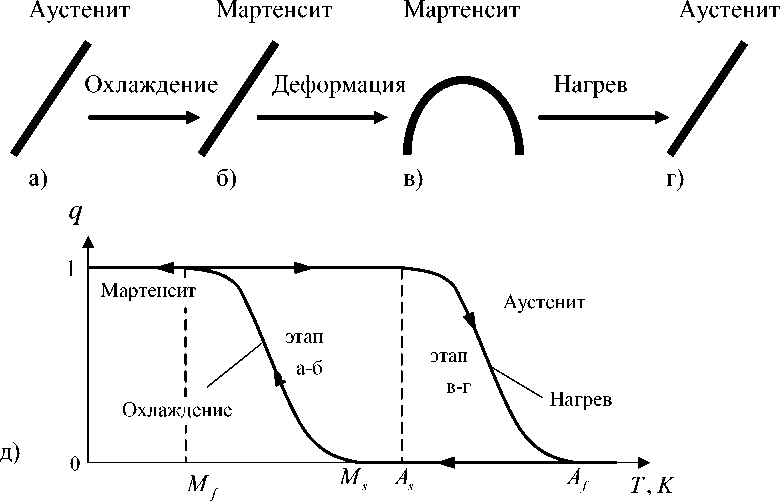
Рис. 1. Схема деформирования стержня с эффектом памяти формы (а–г) и зависимость объемной доли мартенсита q от температуры T (д)

такого материала представлен на рис. 1. Отметим, что деформация на этапе б–в (рис. 1) накапливается за счет переориентации кристаллов мартенсита (эффект мартенситной неупругости) и остается после снятия нагрузок. Эффект памяти формы проявляется на этапе в–г (рис. 1), где материал самостоятельно восстанавливает свою форму и может развить значительные усилия.

К сплавам с памятью формы, кроме NiTi, относятся AuCd, Cu-Al-Zn, AgCd и др. В основе эффекта памяти формы лежат мартенситные превращения, для которых типичны слабая зависимость температур начала и окончания превращения от скорости изменения температуры, чаще всего обратимый характер превращения, заметное несовпадение (гистерезис) температур прямой и обратной реакции и другие признаки [50]. Высокотемпературную модификацию принято называть аустенитом, а низкотемпературную – мартенситом (рис. 1). Температуры мартенситных превращений сильно зависят от химического состава сплавов, их термической и механической обработки. Например, характеристические температуры никелида титана лежат в пределах 30–80°С, редко выходя за этот интервал, однако легирование железом снижает их примерно на 150–200°С, то есть до –170 … –70°С.

Кинетика мартенситных превращений имеет ярко выраженный гистерезис (рис. 1 д). Если материал охлаждать из аустенитного состояния, то вначале каких-либо фазовых преобразований не происходит. Однако, начиная с некоторой характеристической температуры, которую принято обозначать M s , появляются первые кристаллы мартенсита, следовательно, увеличивается и доля мартенситной фазы в объеме материала. По мере дальнейшего охлаждения их размеры и количество увеличиваются, пока кристаллы не заполнят при температуре M f весь объем. Такое превращение называется прямым и при наличии внешней нагрузки сопровождается появлением большой деформации (эффект пластичности превращения). При последующем нагреве, начиная с температуры A s , мартенсит начинает переходить в аустенит. При этом накопленная деформация начинает медленно исчезать, до тех пор, пока температура не станет выше A f и произойдет восстановление формы.

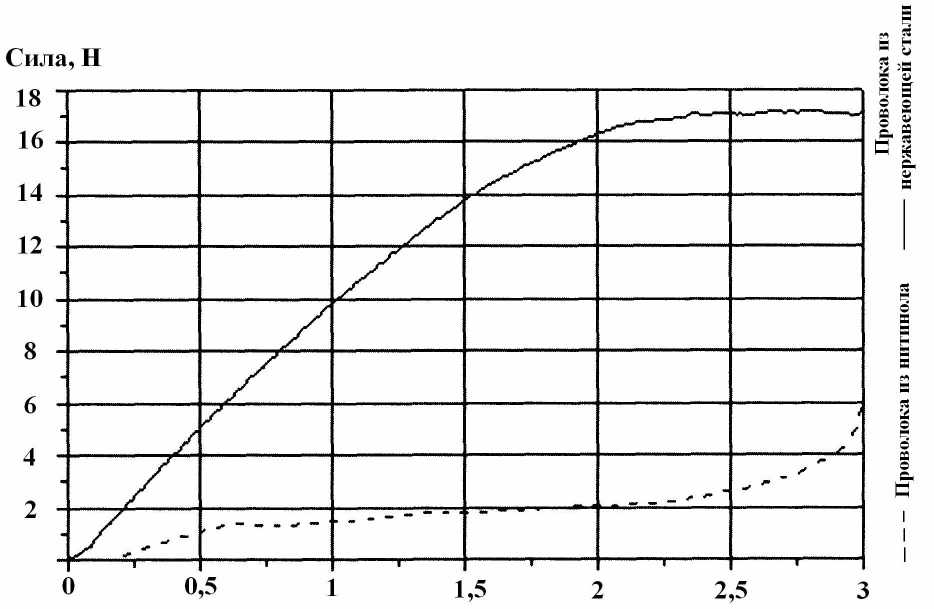
Смещение, мм

Рис. 2. Диаграмма сила - смещение для ортодонтических проволок, изготовленных из сплава с памятью формы и нержавеющих сталей [61 ]

Такие сплавы используются в качестве биомедицинских имплантатов: стентов, ортодонтических проволок, фильтров, фиксаторов, скобок для остеосинтеза, пластинок и т.д. Рассмотрим подробнее эти и другие приложения.

Ортодонтия

Первым предложил использовать нитиноловую проволоку в качестве ортодонтических средств Андрисен ( Andreasen ) [2] в 1971 году, так как она обладает способностью развивать постоянное усилие при различном уровне деформаций. Сплавы с памятью формы обладают практически одинаковым модулем упругости с костной тканью. Ещё один важный показатель - это отношение силы, создаваемой проволокой, к её деформации. В своей статье Андрисен провел сравнение двух проволок из никелида титана с разными температурами превращения на жесткость при возврате формы, так как этот параметр определяет давление устройства на зубы, создаваемое с целью их выравнивания. Необходимость анализа жесткости также вызвана тем, что чрезмерное давление может привести к повреждению твёрдых и мягких тканей, а также к резорбции корня. Жесткость проволоки зависит от модуля упругости материала, из которого она изготовлена, и размеров проволоки. На рис. 2 показаны зависимости сила-смещение для нержавеющих сталей и сплавов с памятью формы [61]. Как видно из рисунка, уже при малых деформациях уровень усилий, создаваемых нержавеющей проволокой, более высокий по сравнению с проволокой из сплава с памятью формы. Это означает, что при одинаковой деформации проволока из нитинола будет создавать меньшее, но постоянное усилие, которое не приведёт к перегружению зубов. Таким образом, работа [2] заложила основы использования нитинола в медицинских целях.

Последующие работы Бурстоуна ( Burstone ) и Кази ( Kusy ) [7, 25] подтвердили уникальные свойства никелида титана по сравнению с традиционными в ортодонтии материалами (кобальт-хром, в—титан, нержавеющие стали). Однако в то время определяющие соотношения для эффекта памяти формы были недостаточно

Рис. 3. Фиксатор, изготовленный из сплава с памятью формы, для остеосинтеза переломов разработаны, и потому в научных статьях были представлены только статистические модели в виде таблиц (размеры→усилия). Похожие статистические модели для никелид–титановых проволок построены российскими учеными в [65]. Более подробно механические свойства ортодонтических проволок из никелида титана при различных видах нагружения (растяжения, изгиба, кручения) рассмотрены в статьях [15, 22, 35]. В работе [15] экспериментально построены таблицы, в которых указаны не только размеры проволок, развиваемые усилия, модули упругости, но и величины энергии, запасаемой в процессе нагружения, и уровень максимальной деформации. Однако аналитические зависимости для определения усилий предложены не были. Можно также констатировать факт отсутствия задач по управлению усилиями проволок из сплавов с памятью формы для оптимального лечения ортодонтических дефектов, а значит отсутствие индивидуального подхода к каждому конкретному случаю.

В работе [11] приведена более тонкая оценка свойств нитиноловой проволоки на основе электросопротивления и построены кривые напряжение – деформация при растяжении с целью получения зависимостей температуры начала мартенситного превращения от величины напряжений M_s ( σ ) . В работе отмечается недостаток стандартизации свойств нитиноловых проволок.

Отдельный класс работ посвящен изготовлению никелид–титановых проволок, где показано влияние процесса изготовления на свойства материала. Например, в работе [1] рассмотрено получение ортодонтической проволоки с помощью порошковой металлургии и показано, что напряжения при прессовке образцов влияют на прочностные характеристики получаемой проволоки и появление нежелательных фаз.

Применение в хирургии и ортопедии

Нитиноловые имплантаты используются также в хирургии для сращения переломов костной ткани [37, 38], коррекции осанки [5], эндопротезов [21, 36, 43, 44], протезов костей [9, 17, 18, 50, 51]. В середине 1970-х годов появились работы [8, 13] по исследованию биосовместимости сплавов с памятью формы с тканями и органами человека, в которых были высказаны предложения по применению этих материалов в качестве имплантатов, протезов костей и других ортопедических приложений. Пионерами в этой области стали учёные из Германии и Китая. Немецкие ученые использовали нитиноловый стержень для лечения сколиоза в 1978 году. В свою очередь, врачи из Китая предложили компрессионную скобу из нитинола. После этого скобки стали применять для сращивания трубчатых костей [64] и отломков нижней челюсти [16, 20]. Техника остеосинтеза переломов нижней челюсти с помощью скобок из никелида титана (рис. 3) представляет собой следующую операцию: хирурги сопоставляют отломки, а затем с помощью бормашины в каждом отломке просверливаются фрезерные отверстия на расстоянии около 10 мм от края перелома строго перпендикулярно с учетом направления компрессионных усилий скобы. Затем скобу–фиксатор в течение 10–15 секунд орошают в хладагенте. С помощью иглодержателей разгибают кольцо скобки, а фиксирующим ножкам придают форму, удобную для введения в кость. Скобу–фиксатор переносят в операционную рану, ножки ее погружают в отверстия в костных отломках и фиксируют пальцем или инструментом в течение 20–30 секунд. При контактном нагревании никелида титана до температуры +35?С скобка стремится принять заданную (первоначальную) форму, за счет чего и обеспечивается компрессия отломков [67]. Несмотря на то, что техника остеосинтеза переломов скобками из никелида титана известна довольно давно, механическому описанию поведения скобки и анализу напряженно-деформированного состояния посвящено мало работ [62, 69, 70]. В работе [62] проведен конечноэлементный анализ напряженно-деформируемого состояния фиксатора с помощью пакета ANSYS. Решению задачи управления напряжениями, которые фиксатор создаёт при установке в костную ткань в результате фазовых превращений, посвящена работа [70].

Фиксаторы из нитинола используются также в качестве протеза стремени [23, 24, 49]. Если в работе [23] исследована биосовместимость протеза с костной тканью у кошек, то в работах [24, 49] гистологические наблюдения проводились на людях.

Ортопедическому применению сплавов с памятью формы в качестве фиксаторов, эндопротезов, протезов костей уделяется большое внимание [18, 36, 44, 50, 51]. В работах [17, 18, 36, 38] наблюдалось взаимодействие ортопедических протезов из никелида титана с костной тканью.

Несмотря на прекрасные результаты, показанные нитиноловыми имплантатами, существуют различные аспекты, связанные с дальнейшим их применением в ортопедии. К дизайну и производству имплантатов должны предъявляться большие требования с целью влияния на их прочностные характеристики. Определенного успеха добились китайские учёные [10, 28], применяющие для производства пористого никелида титана усовершенствованную технологию самораспространяющегося высокотемпературного синтеза. Пористый никелид титана, полученный по данной технологии, обладает высокой прочностью, практически одинаковой плотностью и модулем Юнга с костной тканью. Более того, температуры фазовых превращений пористого нитинола могут быть приведены к значениям, удобным для медицинского применения, путем отжига. Также ведутся разработки по применению и других материалов из сплавов с памятью формы, кроме никелида титана, в качестве ортопедических протезов.

Следует отметить отсутствие аналитических алгоритмов, которые могли бы объяснить с точки зрения биомеханики адекватность использования протеза, изготовленного из сплава с памятью формы, а также расчёта его поведения в костной ткани человека.

Применение в кардиологии и сердечно-сосудистой хирургии

В 1983 году врачи Крэг ( Cragg ) [12] и Доттер ( Dotter ) [14] независимо друг от друга опубликовали свои работы по использованию нитиноловых стентов в сердечнососудистой хирургии. Вследствие отсутствия апробированной техники установки стентов эксперименты были непродолжительными. При установке стента врачу необходимо учитывать различные факторы, одним из которых являются остаточные напряжения в стенках сосуда. Данному аспекту посвящены работы [19, 48, 53, 59]. В середине 1980-х ученые из России занимались изучением биосовместимости и разработкой техники точной установки стентов в различные части сосудов с помощью рентгена [45–47]. Также целью работ являлось экспериментальное определение оптимального размера стента в зависимости от диаметра сосуда. В этом случае критерием оптимальности служило отношение размера стента к диаметру сосуда. Впервые нитиноловый стент был установлен в тело человека в марте 1984 года [46].

Преимущества нитиноловых стентов:

• •    большая гибкость по сравнению со стентами из нержавеющих сталей;

• •    меньшая величина создаваемых напряжений, что характеризуется меньшим риском чрезмерного натяжения сосуда при расширении стента;

• •    биосовместимость и антикоррозийные характеристики;

• •    влияние на перестройку сосуда, влекущее за собой сокращение рестеноза.

В течение последних лет был опубликован ряд работ, посвященных моделированию стентов из нержавеющих сталей и никелида титана и их взаимодействию со стенками сосуда [6, 30–34, 41, 52, 54]. Модели были построены в программных пакетах ANSYS и ABAQUS . В некоторых работах проводилось сравнение сопротивления стентов внешней сжимающей нагрузке [55]. В статье [34] моделировалось влияние геометрических параметров на механические параметры кардиологического стента. Петрини ( Petrini ) [41] использовал конечно-элементную модель для изучения гибкости нового поколения стентов. К сожалению, опубликованных работ, посвященных моделированию стентов, изготовленных из нитинола, относительно немного.

Одними из ключевых работ в этой области являются публикации [33, 56]. При построении модели стента использовалась программа ANSYS . Если в статье [33] поведение стента изучалось в изотермических условиях, то в работе [56] поведение моделировалось при температурах +22?С и +37?С. Одним из перспективных направлений развития применения сплавов с памятью формы в кардиологии является разработка искусственного миокарда [61], а также стентов при заболевании бронхов и трахеите у детей (трахеобронхомаляция) [57]. Внешний вид устройств показан на рис. 4.

В книге Воссуги ( Vossoughi ) [60] отмечается, что после установки стента происходит перестройка сосудов. Сосуды могут изменять свои свойства, структуру, толщину стенки и т.д. Также в работе [60] описываются современные устройства для лечения сосудистых патологий – стент–графты ( stent grafts ), которые начали использовать в последние двадцать лет. Стент–графт это внутрисосудистый стент, покрытый тонкостенным плетеным графтом. Эти устройства позволяют лучше восстанавливать свойства сосудов, обладают большей долговечностью, но ставят перед исследователями более сложные задачи, чем задачи моделирования стентов и графтов по отдельности.

Несмотря на значительные успехи в данной области, существует ряд нерешенных задач с позиций механики, которые значительно бы улучшили качество операций по установке нитиноловых стентов. До сих пор не решена задача

а) стенты [57] (ловушки для тромбов)

б) кардиологические скобки [69]

в) искусственный миокард [63]

Рис. 4. Применение сплавов с памятью формы в кардиологии: а) стенты [57];

б) кардиологические скобки [69]; в) искусственный миокард [63]

оптимизации формы стента и задачи управления формой и усилиями, создаваемыми стентом в сосуде для предотвращения рестеноза.

Гастроэнтерология и желудочно-кишечная хирургия

Новые медицинские технологии в хирургии с использованием сверхэластичных имплантатов представлены в монографиях разделами и многочисленными статьями в торакоабдоминальной и желудочно-кишечной хирургии, гастроэнтерологии и колопроктологии, в хирургии паренхиматозных органов. Впервые разработаны методы компрессионного желудочно-кишечного и межкишечного анастомоза с использованием сверхэластичных имплантатов с памятью формы [67]. Эффективным является способ формирования терминального толстокишечного и тонкотолстокишечного клапанного анастомоза [67, 68]. Разработаны новые принципы оперативного лечения трахеи и бронхов с использованием пористых эластичных имплантатов, близких по поведению к тканям организма. Новые методы позволяют значительно снизить уровень осложнений.

Несмотря на хорошую биосовместимость, существуют проблемы, касающиеся неполного расширения стента, следовательно, в данной области необходимо решать задачи по управлению формой катетера.

Разработка индивидуализированных методов лечения

С точки зрения механики, одним из основных факторов, определяющих успех лечения патологий с использованием материалов с памятью формы, является уровень механических напряжений. Поэтому одним из этапов индивидуального лечения должна быть постановка и решение задачи об управлении напряжениями в живых тканях, вызванными за счет эффекта памяти формы.

Фазовая деформация за счет эффекта памяти формы может быть рассмотрена как собственная деформация [39], под которой понимается неупругая деформация любой природы (температурная, пьезоэлектрическая, пластическая, ростовая, фазовая и др.). Возникают случаи, когда собственная деформация не вызывает напряжений в системе, или, наоборот, не вызывает полной деформации системы (нильпотентная собственная деформация).

Пусть исследуемое тело занимает ограниченную область V трехмерного евклидова пространства E ³. Замыкание области обозначено через V , граница (которая считается достаточно гладкой) - через S ( V = V u S ). Деформации считаются малыми и аддитивными. Тогда тензор малой деформации ε является суммой упругой деформации е e и собственной деформации е *

е = е e + е * , r е V . (1)

Граница области S делится на две взаимно непересекающиеся части: S = S_u ∪ S _σ . На части границы S_u заданы нулевые кинематические граничные условия, на части S _о задан вектор напряжений p :

u = 0, r е S u , n • a = p , r е S _o .

Здесь кинематические граничные условия предполагаются такими, что движение тела как жесткого целого невозможно.

Назовем обобщенным решением задачи симметричный тензор σ , который определяется обобщенным законом Гука a = C -( e ( u ) - е * ) , где u е (W^V ))³, u = 0, r е S u , и для которого имеет место соотношение:

| a •• e ( w ) dv - J p • w ds - J q • w dv = 0, V w е ( W ₂ 1 ( V ))³, w = 0, r е S u .      (3)

V                   S σ               V

Здесь W 2 - пространство Соболева функций, имеющих первую обобщенную производную и интегрируемых с квадратом вместе с производной. Деформации e ( u ) и e ( w ) определяются геометрическими соотношениями Коши, где производные понимаются в обобщенном смысле. Значения перемещений u и w на границе вычисляются посредством оператора следа. В постановке задачи считается, что p е ( L ₂( S _a ))³, q е ( L ₂( V ))³, е * е ( L ₂( V ))⁶, компоненты C_ljkl ( i , j , k , l = 1,2,3) являются кусочно-непрерывными функциями координат.

В работе [39] доказана теорема, что для решаемой задачи обобщенное решение существует и оно единственное.

Для дальнейшего изложения и анализа задачи введем пространство H тензоров деформации, компоненты которых принадлежат функциональному пространству L ₂ . Скалярное произведение и норма в H введены следующим образом:

^{( a} , ^{e )} н = J ^а ••C --^e dv , ||^а|| H = ( KaT tHZ .                        ⁽⁴⁾

V

Далее выделено подпространство H_u собственных деформаций, свободных от напряжений.

Тензор £ е H принадлежит подпространству H u , если существует такая вектор-функция (перемещение): u е (W^V ))³, что u = 0 при r е S u и £ = 0,5( V u + u V ), где производные понимаются в обобщенном смысле, а значение функции u на границе S_u определяется посредством оператора следа.

Собственная деформация, свободная от напряжений, принадлежит подпространству H_u . И наоборот, если собственная деформация принадлежит подпространству H u , то она является свободной от напряжений [39].

Подпространство нильпотентных собственных деформаций H _σ введено посредством условия, что полные деформации системы (1) равны нулю, тогда собственная деформация вычисляется следующим образом

£ ; =- C ^{- 1} -- о , r е V , (5)

где напряжения σ являются статически допустимыми при отсутствии внешних активных сил (уравновешенные напряжения)

j о •- £ ( w ) dv = 0, V w е ( W ₂ 1 ( V ))³, w = 0, r е S u . (6) V

Эти напряжения не ограничиваются классом самоуравновешенных напряжений ввиду наличия реакций опор на границе S_u .

Множество собственных деформаций £ ^ в выражении (5) образует линейное подпространство H _о .

Отметим, что для дискретизированных систем (т.е. ферм или конечноэлементных аппроксимаций) соотношение (6) сводится к уравнениям равновесия узлов. Тогда число линейно независимых решений при определении элементов H _σ равно степени статической неопределимости системы.

В работе [39] доказана теорема, что любая существующая в теле собственная деформация £ * может быть единственным образом разложена на две части, а именно: собственную деформацию, свободную от напряжений, £ U е H u и нильпотентную собственную деформацию £ ^ е H _с :

* * *

^£ = ^£ и ^{+ £} _С ^, r ^{е V} . ⁽⁷⁾

Следствие теоремы о декомпозиции. Если выполнена декомпозиция существующей в теле собственной деформации, то напряжения σ и полная деформация £ тела с собственной деформацией £ вычисляются следующим образом:

о = - C • £,, £ = £ u , r е V . (8)

Таким образом, решение задачи теории упругости с собственными деформациями сводится к выполнению декомпозиции существующей в теле собственной деформации.

Введенные понятия нильпотентных собственных деформаций и собственных деформаций, свободных от напряжений, а также теорема о декомпозиции открывают возможность независимого управления напряжениями (посредством нильпотентных собственных деформаций) и деформациями (посредством собственных деформаций, свободных от напряжений).

Модели, позволяющие описать поведение материалов с памятью формы и свойства сверхэластичности

Для применения теоремы о декомпозиции к решению задач управления необходимо использовать модели поведения сплавов с памятью формы. В данной работе приводится краткий обзор существующих моделей и анализируются две модели: Патора и Мовчана. Стоит также отметить, что, несмотря на большое количество работ по моделированию поведения сплавов с памятью формы, ощущается дефицит работ по применению этих моделей в биомеханике, особенно для решения задач управления напряжениями в биомеханике.

Термомеханическому поведению материалов с памятью формы посвящён ряд работ. Главную роль в поведении сплавов с памятью формы при мартенситных превращениях играет температура, которая выступает как основной термодинамический фактор. Действительно, в некоторых теориях обращается внимание на ограничения, налагаемые положениями термодинамики [65], в других статьях – на традиционные методы механики (которые подходят для решения узкого круга задач) [66], в третьих – на теорию пластического течения (постулат Друкера) [4] и т.д. Для сплавов с памятью формы не существует однозначной зависимости между температурой, напряжением и деформацией, что обуславливает разработку особых определяющих соотношений для этих материалов.

Все существующие модели можно разделить на микроскопические и макроскопические.

В микроскопических теориях рассматриваются процессы деформирования на различных уровнях, таким образом, макроскопическая деформация может быть рассчитана путём осреднения микродеформаций структурных элементов.

В макроскопических теориях устанавливается связь между напряжением, деформацией и температурой, скоростями их изменения, а также структурными параметрами, под которыми обычно понимают массовую долю мартенситной фазы.

Подходы при макроскопическом моделировании включают в себя два аспекта:

• •    определяющие соотношения между напряжением, деформацией и температурой;

• •    движущая сила (зарождение и развитие кристаллов мартенсита) и эволюция фазового превращения (переориентация кристаллов).

С другой стороны, модели можно разделить на:

• •    термодинамические модели;

• •    феноменологические модели.

В термодинамических моделях строятся потенциалы (на основе, например, потенциала Гиббса или свободной энергии Гельмгольца), которые можно разделить на «химическую» часть, зависящую от температуры и включающую в себя энтропию объёмных долей мартенсита, и «механическую» часть, включающую в себя напряжения и деформации при внешнем нагружении и взаимодействии между различными фазами. К таким моделям относятся модели Патора ( Patoor ) [39, 41], Ауриччио ( Auricchio ) [3], Лагудаса ( Lagoudas ) [26], Чанга ( Zhang ) [65] и др.).

В феноменологических моделях определяющие соотношения связаны непосредственно с кинетикой превращения, а условия перехода и накопление доли мартенсита вытекают из экспериментальных диаграмм (модели Мовчана [71, 72], Баумгарта ( Baumgart ) [4], Танаки ( Tanaka ) [56], Лианга ( Liang ) [29]).

Репрезентативными моделями для сравнения феноменологических и термодинамических моделей на основе микромеханического подхода были выбраны модель Мовчана и модель Патора ( Patoor ).

Модель Мовчана [72]

Микромеханический подход Мовчана заключается в рассмотрении зарождения и развития кристаллов мартенсита, которые дают определенный вклад в скорость изменения фазовой деформации в сплаве с памятью формы. Макроскопическая деформация является суммой вклада микродеформаций р , вычисленных по параметру q (доля мартенсита).

Предполагается, что скорость роста кристаллов мартенсита пропорциональна накопленной фазовой деформации и уровню напряжений. В модели учитываются различные упругие свойства аустенита и мартенсита.

Общая схема подхода изложена в [71]. Система определяющих соотношений формулируется следующим образом:

e s ij s ij

+s p ,

где s e , ° ^p - тензоры упругой и фазовой деформации. Для упругой деформации справедливы следующие уравнения:

s

e ' ij

2 G ^,

e

^s kk = к ° kk ,

где G , K – модули сдвига и объемного сжатия, соответственно. Штрих обозначает девиатор соответствующего тензора. Для фазовой деформации используются уравнения:

d s ^p = ( c₀ ° _ij + a₀ s ^p ) dq при dq >  0,                         (11)

ds ij =

q 1 = cos

a 0 ^S ij

V ^(exP^{( a} 0 ) ^- 1)

)

+ a ₀ s ip dq при dq <  0, )

q 2 = cos

n

' T ^{— k} j^ jj ^ ij

—

Mf 1

V

M S — M f

)

при dq >  0,

П

' T — к л — a

A_f — As V ^f S

¹. )

)

при dq <  0,

¹ = q ₊ ^{1 —} q

E ( q )   E 1    E 2

Здесь Е 1 , Е 2 – значения модуля Юнга для мартенситного и аустенитного состояния; a 0 , k , c 0 – коэффициенты материала, которые можно найти из опыта на прямое превращение. Уравнения (11) и (13) соответствуют прямому превращению, а (12) и (14) – обратному. M S , М f , А S , А f – температуры начала и завершения прямого и обратного мартенситного превращения.

выделенный элементарный объём V

АУCТЕНИТ объём V_А

МАРТЕНСИТ объём V_M

зёрна

Т тттшгтттттттттттттт

Σ

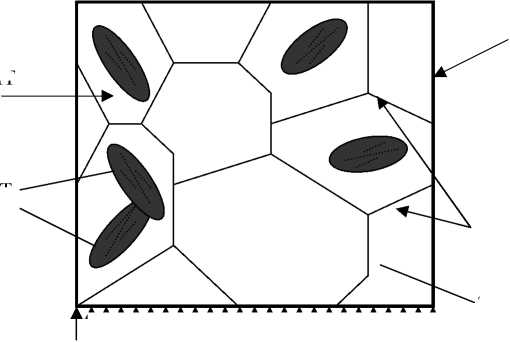
Рис. 5. Выделенный элементарный объём сплава с памятью формы, состоящий из множества аустенитных зёрен, в которых при термомеханическом нагружении появляются мартенситные области

Модель Патора (Patoor) [40]

Модельный объект представляет поликристалл, состоящий из зерен. Зерна рассматриваются в выделенном элементарном объёме. Каждое зерно рассматривается как монокристалл, в котором может образовываться 1,2,… N вариантов мартенсита (под вариантом в данном случае подразумевается мартенситная пластина). Внутри выделенного элементарного объёма (рис. 5) происходит мартенситное превращение, обусловленное механическим или температурным нагружением. Поэтому в качестве управляющих переменных были взяты макроскопическое напряжение Σ и температура Т . Предполагается, что упругие модули С ijkl одинаковы для обеих фаз.

Тогда макроскопическая деформация равна сумме упругой деформации E_i^e_j и деформации фазового перехода E_i^T_j :

E.. = Ee + ET.(16)

ij               ijij

Макроскопическая упругая деформация равна:

Ee = ci x и,(17)

где C - kll - тензор податливости четвертого ранга, 2 _kl - макроскопическое напряжение.

Макроскопическая деформация фазового перехода равна среднему значению микроскопической деформации г T по объему выделенного элемента:

ET = | Й T (r) dV.(18)

VV

Учитывая, что микроскопическая деформация фазового перехода определена только в мартенситной части объема, а в аустенитной фазе она равна нулю, получим:

E T = 1Г I ^е T (r ) dV .                              (*9)

V_M M

Доля мартенсита определяется как отношение объёма, занимаемого мартенситом, к общему объёму выделенного элемента:

f = VV , 0 <  f <  1.                            (20)

Тогда

E = f E T .                                   (21)

В модели используется предположение, высказанное в [27], что эквивалентная деформация фазового перехода E T q достигает насыщения при значении E Ta _x , т.е.

е ^T <  е ^T ,

eq max ,

T TT д eq 3 ij ij .

Эволюция макроскопической деформации E ij определяется изменением термодинамического потенциала Гиббса ψ, который является функцией управляющих параметров (приложенного напряжения 2 ^. и температуры Т) и системы внутренних переменных f (объёмная доля мартенсита). Потенциал представительного объёма, претерпевающего мартенситное превращение, включает в себя химическую энергию, упругую энергию и энергию межфазной границы:

^^{( 2} j , ^T , ^f )    ^^потенциальная

—

w упругая

-w -w , .

химическая межфазная .

Химическая энергия ( W химическая ) в первом приближении линейно зависит от температуры, а величина энергии межфазной границы ( W межфазная ) пренебрежимо мала по сравнению с другими слагаемыми.

W ,    =0.

межфазная ,

W =В(Т-ТЛГ.

химическая              0     ,

где В – химическая постоянная, Т – текущая температура, Т 0 – температура термодинамического равновесия.

Потенциальная энергия ( W потенциальная ) для представительного объёма имеет вид:

W          (2.., f , 8^T. ) = 2. E . =Z. C —1 2,,+s. .8^Tf .

потенциальная ij ,    , ij           ij ij ij ijkl kl ij ij .

В соответствии с тремя уровнями, на которых рассматривается структура выделенного элемента, упругая энергия может быть разделена на три слагаемых:

w =w +w +w упругая макроскопическая межгранулярная межвариантная ,

1 e 1          TT 2    1             2

упругая 2 ij ij 2 зерна ij ij        2 варианта ,

где H _зерна и H _{варианта} – величины, определяющие взаимодействия между зернами и вариантами мартенсита, соответственно.

В итоге, при подстановке (24), (25), (26), (28) в (23) потенциал для свободной энергии Гиббса имеет вид:

ш(Е. , T , f , 8 T ) = ¹S. C - 1 S_w+S..8 T f - B (T - T ) f - ¹ H   8 T 8 T f ² -¹ H     f ². (29)

ij ’ J ’ ij '     2 ij ijkl kl ij ij"         '         0 / J 2 зерна ij ij J 2     варианта J     V /

В модели Патора ( Patoor ) пренебрегается объёмным эффектом при мартенситном превращении, тогда шаровая часть тензора 8 T равна нулю. С учётом этого выражение (29) примет вид:

У( Е „ , T , / , 8 T ) = 1 S ij Cl S k, + S i, Ё T f - B(T - T o ) f - 2 H „р„ Ё T 8 T f¹ - 1 H ^_a f ² , (30)

где S = ^s -j ^ - девиатор напряжений.

В модели вводятся три множителя Лагранжа, связанные с долей мартенсита и средней деформацией фазового перехода:

^(0 - f ) = 0, X 1 ( f - 1) = 0, X 2 (С -Ё ^_х ) = 0.                 (31)

Функция Лагранжа в этом случае записывается в виде:

L ( S j , T , f , Ё T ) = у( Е _у, T , f , Ё T ) + X 0 f -X , ( f - 1) -X 2 ( s T q -Ё ^а_x ).          (32)

Минимум функции Лагранжа достигается в точке ( f , 8 T ), где градиент равен нулю. При дифференцировании функции Лагранжа по внутренним переменным (доля мартенсита f и средняя деформация фазового перехода ε _i ^T _j ) можно получить термодинамическую силу ( Ff ) и силу ориентации ( F^ ):

F f =d f; (X ij , T , f , Ё T ) = S ij -Ё T - B ( T - T 0 ) - H зерна Ё T Ё T f - H варианта f + X 0 -X , ,    (33)

∂ ε ^T

F =     (s,, t , f , ё T ) = S, f - я „J T f - H_eamaHmaf -x₂ -^q .

^Ё ij    d8 jV i J    i.)      ^ijJ зерна ij J вариантам ² ds T

Предполагается, что когда термодинамическая сила Ff достигает критического значения, начинается рост мартенситных пластин. При достижении силой ориентации F_8j некоторого критического значения начинается переориентация зёрен мартенсита.

Сравнение моделей

Одной из задач работы является сравнение и анализ возможности применения рассмотренных моделей к задачам механики, в частности, к задачам биомеханики. Модель Мовчана включает в себя двенадцать материальных констант, в то время как модель Патора - шесть. Однако модель Патора, в отличие от модели Мовчана, не учитывает различия в упругих свойствах аустенитной и мартенситной фаз. Преимущества модели Мовчана заключаются в наличии аналитических решений, позволяющих создавать инженерные методы расчёта напряженно-деформированного состояния тел сложной формы. В свою очередь, модель Патора в рассмотренном эксперименте позволяет точнее описать процесс разгрузки мартенсита.

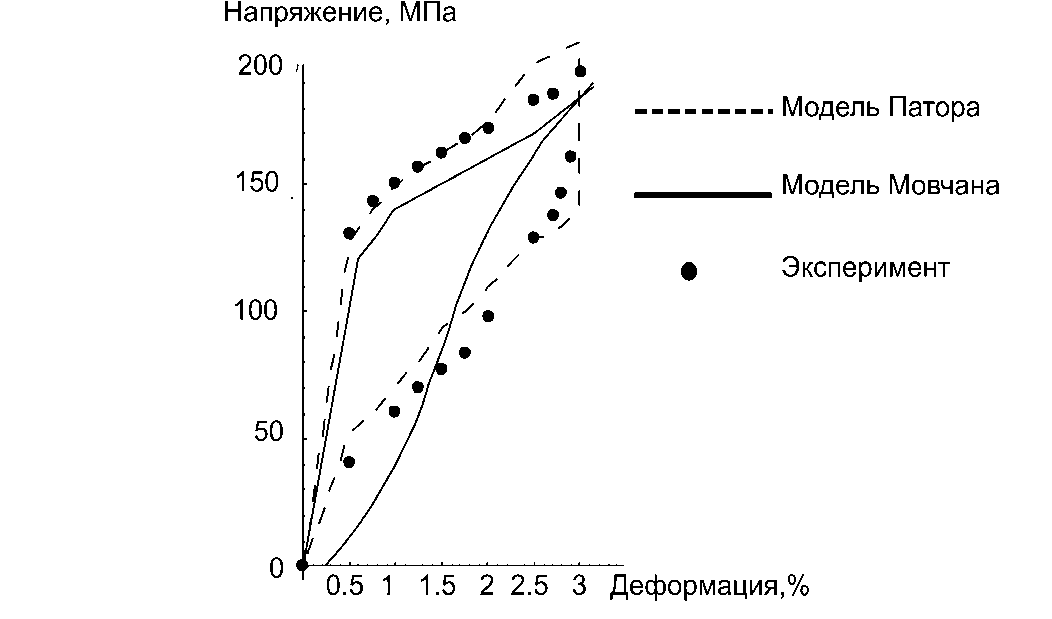
Рис. 6. Кривые в координатах напряжение – деформация для сплава с памятью формы (Cu-Al-Be): экспериментальные точки и вычисления по моделям Мовчана и Патора ( Patoor ) при температуре Т =20?С

Для сравнения моделей из статьи [42] была взята диаграмма растяжение – сжатие, описывающая поведение сплава с памятью формы (Cu-Al-Be). Эксперимент на растяжение стержня из сплава с памятью формы проводился при температуре T = 20?C. На диаграмме были показаны экспериментальные точки и кривая, построенная по модели Патора. Также в статье были приведены значения некоторых параметров сплава, в том числе и температуры мартенситных превращений. В работе [72] были получены аналитические решения для растяжения стержня в изотермических условиях по модели Мовчана. По экспериментальным точкам, используя метод наименьших квадратов, были получены значения коэффициентов a 0 , c 0 и k . В результате по модели Мовчана была построена диаграмма растяжения для данного сплава при T = 20?C. Диаграмма растяжения, соответствующая модели Патора, построена в работе [42]. Из рис. 6 видно, что обе модели удовлетворительно описывают накопление фазовой деформации во время прямого фазового превращения (эффект пластичности превращения) и могут использоваться для решения задач управления, так как именно этот переход определяет накопленную фазовую деформацию и, следовательно, создаваемые напряжения. Поскольку модель Мовчана позволяет получать аналитические зависимости для фазовой деформации, то ее использование предпочтительнее, особенно при решении задач управления.

Благодарности

Работа выполнена в рамках Соглашения о сотрудничестве между Венским техническим университетом и Пермским государственным техническим университетом. Работа выполнена при поддержке РФФИ в рамках проекта № 07–01– 96061-р-Урал-а.