Sports technique information entropy: ways to overcome and opportunities to use

А.А. Померанцев, , Липецкий государственный педагогический университет имени П.П. Семенова-Тян-Шанского, Липецк, Россия

Introduction. Qualitative and quantitative biomechanical analysis is used to analyse sports technique [11]. Qualitative analysis is based on visual assessment. Quantitative analysis is based on the application of instrumental biomechanical control methods [9]. Qualitative analysis is based on comparative adjectives, quantitative analysis – on numbers [4, 15]. The main advantage of visual control is its promptness. Despite the technological progress, qualitative biomechanical analysis remains the main tool for improving sports technique from beginners to high-level athletes [7, 10, 12, 16]. However, the possibilities of visual perception are limited by the physiology of the sensory visual system. The conclusions about sports technique may be biased depending on the sports and coaching experience of the experts. Visual control allows correcting gross technique errors that are visible by the ‘naked’ eye [18, 22].

The concept of sports technique strives to strict biomechanical standardization through the description of kinematic and dynamic characteristics. But it does not have an unambiguous biomechanical interpretation [8, 14]. The optimal technique model may differ greatly depending on the somatic parameters (height, weight and body proportions), motor qualities and skills. Different experts can identify error by analysing the technique of the same athlete. Thereby technique may be evaluated as correct or incorrect [21].

Relationship between the perception subjectivity and informational uncertainty of human movements is dialectic of sports technique cognition.

Clear relationship between the biomechanical parameters of sports technique and athletic performance is incomprehensible. So, coaches build technique training on the athlete responsiveness as a system. It means that the effectiveness and correctness of sports technique is evaluated in comparison with sports results. The goal of modern sports biomechanics is the rejection of ‘the black box’ approach by reducing the uncertainty level of visual assessment and a strict understanding of movement biomechanics as a system. However, absolute clarity of technique understanding along with usage of qualitative biomechanical analysis is unattainable due to the uniqueness of motor actions [1, 17, 19]. The uncertainty of technique perception will always remain [13].

The sports technique improvement is a longterm continuous process. A coach by fixing the error and correcting the technique assumes that it will lead to improved athletic performance. The perception subjectivity and technique uncertainty form the dialectic of technique perfection. A limited visual system and lack of technique standardization led to information uncertainty. Overcoming the technique uncertainty is the way to further cognition of sports movements and improvement of qualitative biomechanical analysis.

The research hypothesis implies that the perception of sports movement and information entropy can be quantified by mathematical and statistical methods. Information entropy should become an informative indicator of skill levels along with such indicators as efficiency, rationality, economy, stability and variability [3].

The aim of this study was to improve qualitative biomechanical analysis by reducing information entropy in the perception of sports technique.

Table 1

Experts’ features

Expert	Working experience, years	Grade	Errors identified
#1	48	Honored Coach *	57
#2	12		68
#3	3		59
#4	8	Top-tier coach *	71
#5	4		51
#6	5		68
#7	2		48
#8	34		57
#9	33	Top-tier coach *	38
#10	47	Honored Coach*	66

*These coaches have extensive experience in preparing athletes for international competitions, including the Olympic Games.

Materials and methods. The research was based on expert assessments. The study involved ten athletes aged 17–18 years. The video of their sprint running was prepared for analysis in advance. All athletes were physical education students from different sports. However, all of them have known the basics of sprint running.

Then, we showed our slow-motion video to 10 real track and field coaches (Table 1).

The study involved several methods:

• (1)    The method of high-speed video capture.

• (2)    The method of expert assessments.

• (3)    Mathematical and statistical analysis.

The method of high-speed video capture

Each athlete had 35 meters of start zone. It was enough for acceleration to maximal velocity. The athletes were given the setting to run at maximum speed. Two strides were completely got in the camera lens. The shooting was carried out with a Fastec InLine digital slow-motion camera with a shooting speed of 250 frames per second and resolution of 640×480 pixels (Fig. 1). The long-focus Navitar lens was used to eliminate distortions. The shutter speed was 0.001 s.

Fig. 1. Two frames of high-speed video

The method of expert assessments

In advance coaches discussed and formulated 16 typical errors that were most common in sprint running and described in the special literature [5, 6, 23]. Thereby, the coaches did not disagree on the wording and interpretation of motor errors in sprint running before the expert assessment (Table 2).

Based on their personal experience and knowledge, experts evaluated sports technique by using a ten-point scale. The results of expert

Table 2

Typical errors in sprint running

#1. Insufficient carryover of the thigh forward and up	#9. The arms are not pulled back enough
#2. The lack of active propulsion of the pelvis forward	#10. Excessive torso forward tilt
#3. Incomplete repulsion	#11. Excessive torso back tilt
#4. Incorrect foot statement	#12. Leg flexion during its setting
#5. Foot landing from heel to toe	#13. Head down
#6. Excessive stiffness	#14. Hands are tense
#7. Excessive angle of elbow joint	#15. Slow thighs bringing together
#8. Hand movements are incorrect in the transverse plane	#16. Head dipped back

Table 3

Protocol form with expert assessments (expert #5 data example)

Athletes	General assessment*	Technique errors **
#1	3	1, 2, 6, 8, 9, 12, 15
#2	6	8, 2, 5, 4
#3	5	10, 1, 2, 7, 15
#4	3	1, 2, 5, 6, 8, 12, 14
#5	7	2, 5, 7, 12
#6	3	1, 2, 4, 7, 12, 15
#7	4	2, 5, 4, 8, 10, 16
#8	3	1, 2, 5, 6, 8, 9, 12, 14
#9	7	9, 10, 12, 13
#10	5	1, 2, 5, 9, 12, 16

* Scores were set in the range from 1 to 10. A score of 10 points corresponded to the best technique.

** Errors numbering is shown in accordance with Table 2.

assessments were recorded in the research protocols (Table 3).

The experts evaluated the technique separately from each other, which eliminated the possibility of comparing their assessments, as well as revising and making adjustments to the expert estimates. The experts were only offered the video sequence for analysis; they were not given any information about the kinematic or dynamic parameters of the technique. It should be mentioned that none of the athletes was a trainee or a rela- tive of any of the experts. Thus, an evaluation bias was ruled out. Also, there were no injured athletes among those under study.

Mathematical and statistical methods

Expert consistency determining. We used the Kendall's concordance coefficient to assess opinions consistency of qualified coaches. Since in some cases experts gave athletes equal points for their technique the concordance coefficient was calculated using the following formulas [2]:

s

7^m² (n ³ -n)-m^ jL₁ T j ,

w =

where

^T = /                               (2)

5 = Z ”₌i {z m=i *⁶->(^ + i)}²;         (3)

n – number of athletes whose technique is evaluated;

• m – number of experts;

x ij – rank of the i -th athlete, which is assigned to him by the j -th expert;

t j – number of identical ranks given by the expert.

In the context of the research, the focus is made not on the assessment of certain athletes but on the consistency of the experts' opinions.

Information entropy calculating. It is impossible to define unequivocally which expert is right or wrong in each case. Therefore, we can talk about uncertainty in the perception of sports technique. Information entropy is usually understood as an information lack after all previous information has been taken into account [2, 24].

Information entropy with n discrete outcomes, each with probability P i , is determined by the Shannon's formula [20]:

H = -^ > ₌ i P_i\og 2 P t , (4) where i = 1, 2, …., n.

Experts evaluated sports technique based on 16 typical errors. Every error can be formalised as 1 – in the case of registering or 0 – in the case of its absence. So, the maximum range of outcomes for a certain athlete is 1111111111111111 in binary calculation or 216 – 1 = 65535 possible combinations.

To this value is necessary to add another potential outcome when the athlete's technique will be without errors. This case in binary calculus will be 0000000000000000. Based on this, we used the formula (4) to find the maximum level of entropy considering that all outcomes are equivalent.

^H _max = ⁶⁵⁵³⁶ х (^ х lOg 2 ^^¹^ )=

= 16 bit. (5)

Thus, each bit of information encodes one technique error. The state when H = 1 bit for one error means complete uncertainty, i.e. experts are equally likely to detect or not detect the sport technique error.

Data collection. Digitization of experts’ record sheets allowed forming a primary data array with the number of dimensions 10 experts × × 10 athletes × (16 errors + 1 general assessment

Table 4

Results of expert valuation of sprint running technique (general assessment)

Experts	Athletes
	#1	#2	#3	#4	#5	#6	#7	#8	#9	#10
# 1	3/9*	5/5	4/8	3/9	7/1	6/4	5/5	7/1	7/1	5/5
# 2	7/3	7/3	8/1	7/3	7/3	6/8	8/1	7/3	6/8	6/8
# 3	6/3	6/3	7/2	4/9	8/1	5/7	6/3	5/7	6/3	4/9
# 4	7/1	6/2	6/2	4/5	5/4	4/5	4/5	3/10	4/5	4/5
# 5	3/7	6/3	5/4	3/7	7/1	3/7	4/6	3/7	7/1	5/4
# 6	5/5	5/5	8/1	4/10	5/5	5/5	7/3	5/5	8/1	6/4
# 7	6/2	5/6	5/6	5/6	6/2	4/10	7/1	6/2	6/2	5/6
# 8	7/1	6/4	6/4	7/1	6/4	7/1	6/4	6/4	5/9	5/9
# 9	4/3	3/5	6/1	6/1	3/5	3/5	3/5	4/3	2/10	3/5
# 10	6/3	5/8	6/3	7/1	6/3	5/8	6/3	6/3	7/1	5/8

* Rating given by the experts on a 10-point scale. Rank indicated under slash.

(Table 4)). Thus, primary data array included 1,700 values.

Results

Expert consistency

Having determined the value of S = 1172 and using formulas (3) we found the concordance coefficient W = 0,15 (1), (2). According to statistical standards expert opinions are considered consistent only when W > 0,6.

Low experts' consistency means that there is no opinion commonality. This once again confirms that qualitative biomechanical analysis is subjective and it can’t be the basis for strict technique assessment and corrections at present. Experts perceive the sport technique based on their own ideas, experience and intuition.

Information entropy calculating

Entropy is directly related to the quality of information. The higher the class of experts and their consistency, the lower uncertainty level and more complete information.

Table 5 shows an example of technique error entropy calculating.

We can find from example that:

Error probability P 1 = 6/10 = 0,6;

Absent error probability P 0 = 4/10 = 0,4;

Information entropy (4):

H 1:6 = – ((0,6 log 2 0,6) + (0,4 log 2 0,4)) = = 0,97 bits.

Similarly, we calculated information entropy for all 16 technique errors of athlete #1 (Table 6).

The maximum 1 bit entropy will be when there is an equal probability (0,5) of error presence and absence. It means that 5 experts registered the error and 5 experts did not register it.

Subjective perception and technique uncertainty are two manifestations of the same process that determines information entropy. The technique entropy of 10 athletes lies in the interval from 9,56 to 11,68 bits (Table 7).

In addition to the absolute sports technique entropy, it is advisable to find the relative entropy (E). Relative entropy shows the ratio of information uncertainty (H entropy) to the total volume of possible information (H max ).

Е = ^- х 100%.                    (6)

For example, the technique entropy of athlete #1 is H = 11.34 bits (Table 6). The total information volume for 16 errors is U = 16 bits. Thus, relative information entropy accounts Е _ 11,34 bit х ioo% _ 71 % for the total volume 16 bit of information.

Table 7 also shows the average probability

Table 5

Identifying the technique error #6 entropy of the athlete #1 (“Excessive stiffness”)

Experts	#1	#2	#3	#4	#5	#6	#7	#8	#9	#10
Error registering	1	1	0	1	1	0	0	1	0	1

Table 6

Calculation of sports technique integral entropy (U) for athlete #1, bits

Errors																H 1
#1	#2	#3	#4	#5	#6	#7	#8	#9	#10	#11	#12	#13	#14	#15	#16
1,0	,97	1,0	,88	,72	,97	,47	,72	1,0	0,0	,47	,97	,47	,72	,97	0,0	11,34

Table 7

Sports technique uncertainty indicators

Athlete	Sports specialization	V*, m/s	H, bits	_ P	E, %
#1	Athletics	7,01	11,34	0,59	71
#2	Ice hockey	7,51	11,44	0,63	72
#3	Swimming	8,55	10,72	0,73	67
#4	Orienteering	7,44	10,09	0,63	63
#5	Rowing	7,82	9,56	0,69	60
#6	Volleyball	6,56	10,57	0,58	66
#7	Powerlifting	7,75	11,68	0,64	73
#8	Boxing	7,73	10,76	0,63	67
#9	Basketball	8,73	11,57	0,65	72
#10	Football	7,96	10,38	0,58	65
		7,70 ± 0,65	10,81 ± 0,70	0,63 ± 0,05	68 ± 4,1

* The running speed was determined using Kinovea software [7] as the average speed for 2 running strides.

of registering technique errors ( P) . This indicator was defined as the ratio of registered errors to total number of possible errors.

P _ registered errors

— 16 errors X10 experts'

In our example, experts registered a total of

94 errors for athlete #1. Thus, P _ — = 0,587 .

Discussion and implications

The rule of sports technique improvement from the position of information entropy

We found a curve that restricts the area of potential technique uncertainty by plotting function (4) for 16 errors (Fig. 2). Umax = 16 bits.

There are two states of maximum clarity for experts: newcomer's state, when experts register the maximum number of errors, and elite athlete's state, when experts do not find any gross technique errors at all. Thus, to characterise sports technique besides entropy calculated in bits it is necessary to identify its type.

The entropy type is determined by sport technique errors probability ( P ).

The value P > 0,5 indicates the initial phase of sports technique formation and P < 0,5 indicates the completion phase.

The information uncertainty is reliable indicator of technique skills improvement, along with such indicators as efficiency, rationality, stability and variability of sports technique .

Estimation of sports technique errors formulations from perspective of entropy

Unequal coach experiences lead to interpretation of qualitative motor errors in different ways. The clearer motor error is formulated, the more unambiguous is the interpretation and the lower uncertainty level.

The proposed approach allows identifying the most reliable details of sports technique and discarding criteria with the highest level of information entropy.

We calculated the aggregate entropy for each error. Since the experiment involved 10 experts and error was encoded as 1 or 0, the information entropy maximum can be 10 bits.

Fig. 3 shows the aggregated entropy values for each error.

The graph shows that majority errors have probability P < 0.5. Errors # 2, # 6, and # 5 have a probability P > 0.5, so they are the most frequent, and probably the most difficult to correct.

Errors #12, #3, #14, #4, #2 have the highest entropy. It means that they are the most controversial and they are inaccurately formulated. Relative information entropy of these errors is ~90 %.

Thus, each of the 16 sport technique errors proposed by the coaches can be characterised from the position of information uncertainty. Less entropy may indicate that the error is unambiguously interpreted and that its registration is less controversial. Criteria for sports technique evaluating with the least entropy will be the most objective and informative.

Conclusions

The study revealed that a significant part of information on sports technique is uncertain. Qualitative biomechanical analysis remains highly subjective and depends on coach experience and biases.

The information entropy is the reliable indicator of technique skills improvement along with such indicators as efficiency, rationality, stability and variability of sports technique.

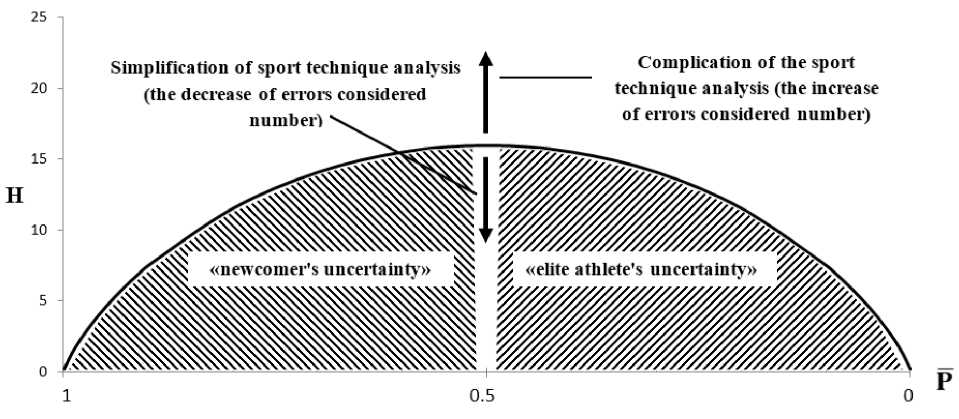
«newcomer's uncertainty»

«elite athlete’s uncertainty’»

Simplification of sport technique analysis (the decrease of errors considered number)

Complication of the sport technique analysis (the increase of error’s considered number)

Fig. 2. The change of sports technique uncertainty during sports skills improvement

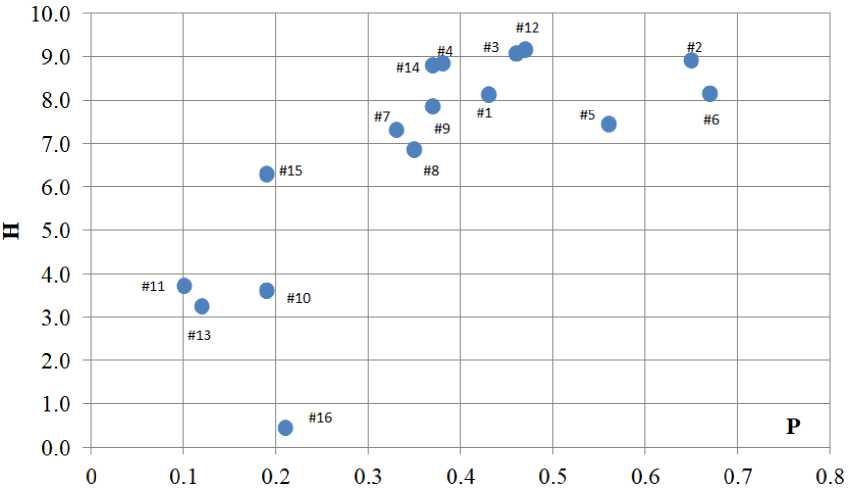
Fig. 3. The relationship between the information entropy (H) and the error probability (P)

Technique errors can be characterised according to their entropy. Clear formulation of motor errors when different interpretations are impossible allows clarify the concept of sports technique.

The proposed method can be used to revise sports technique evaluation and improve the judging quality in sports with subjective assessments.