Способ минимизации дизъюнктивных нормальных форм булевых функций



СПОСОБ МИНИМИЗАЦИИДИЗЪЮНКТИВНЫХ НОРМАЛЬНЫХ ФОРМ БУЛЕВЫХ ФУНКЦИЙ

Р. Н, Песков, В. Н. Щенников

Рассмотрена задача минимизации булевых функций в классе дизъюнктивных нормальных форм- Приведено описание метода, использующего разложение в виде декомпозиционного дерева, для поиска простых импликант. По импликант-ной матрице строится система ограничений и составляется задача линейного программирования. Предложено использовать разбиение системы ограничений в случае большого количества переменных.

Существует большое количество алгоритмов минимизации булевых функций в классе ДНФ. Их обзор и классификация достаточно полно даются в [3]. Переформулировка задачи минимизации в терминах целочисленного линейного программирования приведена в работе [2]. В настоящей статье предлагается модификация этого метода, которая ускоряет поиск минимальной ДНФ.

Прежде, чем воспользоваться аппаратом линейного программирования, необходимо найти все простые импликанты булевой функции. Введем определения из [1]:

Определение 1. Булева функция д = s(ti, ...дЖп) называется импликантой булевой функции / = Дш,..., тД, если па любом наборе значений переменных xi,..., х_п, на котором значение функции д равно единице, значение функции / также равно единице.

Определение 2. Простой импликантой функции / называется всякое элементарное произведениед ~ х^х^.-.хц, являющееся им-пликаптой булевой функции /, и такое, что никакая его собственная часть (т. е. произведение, получающееся из произведения д вы брасыванием одного или нескольких сомножителей iij) уже не является импликантой функции /.

Для поиска простых импликант в работе [2] предлагается использовать алгоритм Куайна-Мак-Класки, который является наиболее распространенным. В настоящее время существует способ разложения булевой функции в виде декомпозиционного дерева [4}, который имеет меньшую временную сложность, чем алгоритм Куайна-Мак-Класки.

Декомпозиция есть разбиение функции / на две функции Д и ft, которые определяются положительным и отрицательным значениями входной переменной т,:

/о ⁼ /(^-1з ■ ■ - з т,—1, 0, Жг-^1, - - - , Zfc)

D1' ■ W

/1 f^$h • ■ ■ ,Xi-l, I,Xt+l, - . - , Тй).

Декомпозиция D_tDj - это комбинация Dt-й и Dj-й декомпозиции:

/оО    /(^-11 * * ■ ; Xi — 11 б, Xj-^. 1, . . . , Tj —1,0, X j + 1, - ■ ■ , Zfc )

Zpi    / (^11 ■ ■ ■ > -®i — li6,Z^i,...,X,'— 1,1, 21j+i, . . . , Zk)

DiDj :                                                                          (2)

/10      J (*^11 ■ ■ ■ з Ti —1, 1, Zj-|-1, . . , , Xj— 1,0, Zj-|-1, . , . , Xfc)

/11      J ("^ 1, ■ • ■ f Xi — 1, 1, Zj-f-1, . . . , Tj — 1, 1, Tja 1 r ■ ■ ■ з Xk )-

Полное описание алгоритма приводится в [4]. Здесь используем его только для опреде ления всех простых импликант в описываемом примере.

Пусть функция / четырех переменных задана последовательностью нулей и единиц своих значений: 1101010110001100. Будем также получать функции у,, = /о A f{,i = 1,4. Первый уровень дерева будут составлять декомпозиции Di, D2, Ds, D4.

11010101	11011000	11011011	10001010
Di :      Л1О0О1100; О2	:     Л01011100; j	Оз :      Л01010000;	04 :     ЛИ 110010.
gi = 10000100	92 = 01011000	дз = 01010000	94 = 10000010
Второй уровень:
	1000	1001	1000
D12 :	Л0100; /Да :	Л0000; П14 :	лоощ
#12 -	= 0000        913	= 0000       914	= 0000
	оно	0010	0000
^23 :	Л0100; Ю24 :	Л1100; Р34 :	л иоо.
#23 :	= 0100       924	= 0000        9з4	= 0000

При последующем разложении все функции д будут равны 00, поэтому нет необходимости построения третьего уровня.

По лемме 3.1 из [4]: если д^а^, ...^а^ = 1, то р = х^Т^-'-Х^ импликанта функции /, где

* х Xi, a_t = 0.

Тогда, учитывая, что часть импликант первого уровня будет поглощена импликан-тами второго уровня, для примера, описанного выше, получим 6 простых импликант: Х2Ж3Х4, Х2Х3Х4,11X3X4, Х1Х4,Х1Т2Хз, X1X2X3.

После того как все простые импликанты были определены, необходимо построить им пликантную таблицу. Импликаптная таблица функции / представляет собой прямоугольную таблицу, строки которой обозначаются различными простыми импликантами функции f, а столбцы - наборами значений переменных, па которых функция обращается в едшЕицу (копституентами единицы). Правило заполнения импликантной таблицы следующее: на пересечении р-й строки и А'-т столбца импликантной таблицы тогда и только тогда ставится метка, когда импликанта р составляет некоторую часть копституенты К (возможно совпадающую со всей конституеп-той).

Для примера, описанного выше, импли-кантная матрица имеет вид:

	=1=2Т374	i1^2i:3z:4	х^^з *з®4	2,12=3=4	Т,Т2тЗ=4	Ti=2=3x4	ZL^З^З®^	T I ЕЕ 2 т 3^4
= 1=4		*		*	*	*
=1=2=’з							*	+
=1=3®4			*				*
=2=»=4					*			*
T2S3X4	*		*
Ti^^a		*

Если в каком-либо столбце имеется только одна метка, то импликанта, стоящая в соответствующей строке, является существенной - без нее не может быть получено покрытие всего множества импликант данной функция. Так как существенные импликап-ты в любом случае должны входить в ми нимальную форму функции, то можно сразу включить их в минимальную форму и не рассматривать далее. Поэтому можно сократить количество операций, исключив из таблицы соответствующие им строки и столбцы тех коиституеит, которые покрываются ими. Для рассмотренного выше примера получим:

	$ 1 з^2 ^3^4		ElE2i:gT4	Щ£ Я12Я!5ЯГ4
я^З^з			*	*
^1^3 ^4		*	*
112^3*4				* -
^2 ^3^4	*	*
$1$2$3	*

На втором этапе необходимо из простых импликант выбрать минимальное их количество так, чтобы покрывались все конституен-ты. Из таблицы получим систему ограничений

У^ ари, 5 Д J — 1? 2,..., t, (3) »=1

где коэффициент а^ равен 1 или 0 в зависимости от того, стоит ли метка в j-м столбце г-й строке импликантной таблицы, а и, соответствуют простым импликантам ре Для получения кратчайшей ДНФ минимизируется линейная форма

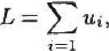
при условии системы ограничений (3) и что щ равно 1 или 0.

Для рассматриваемого примера система (3) и форма L будут следующие:

' U4 + Us > 1, U2 + U4 > 1, Ul + U2 5 Ij

, щ 4- из > 1.

L = ui + иг + из + ii4 + us-

Таким образом, получается задача целочисленного линейного программирования. В математическом пакете Mathematica с помощью функции LinearProgramming находим решение: ui — 1, иг = 0, из = 0, «4 = 1, us = 0. Отсюда следует, что в кратчайшую ДНФ будут входить первая и четвертая им-пликанты. Добавив их к существенной им-пликаите, определенной ранее, можно получить минимальную ДНФ:

271^2^3 V Я2Т3Т4 V Т1Т4.

В комментариях к [2] указано, что импли-кантная таблица будет иметь размеры поряд-ка т х t - 2" х 2" - ^1^(1-^ ₀< _е< _lf

£ —> 0 при п -> оо [4]. Поэтому для функций большого количества переменных может потребоваться огромное количество вычислений. В таких случаях предлагается воспользоваться расчленением ограничений.

Пусть дана система ограничений (1): Ли > 1. Представим матрицу коэффициентов в виде

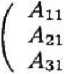
Л12

Л 22

Л32

Л1з

Л23

Лзз

Введем в рассмотрение матрицы Ai и Аг, т. е.

/ Ац А12 Y л _ / Л 22 Азз \ У А21 А22 / ² \ ^32 А33 у

Матрица Ло = А22 ■

Получим две задачи линейного программирования:

Li = У^ u^ -> min i=l

Aiu(1) > 1

0 < ж(1) < 1

L2 = у^ ^F^ ~*m™

Аги^ > 1

0 <  x^W < 1.

Решив их, найдем L — Li + L^.

Переставляя строки в импликантной таблице таким образом, чтобы в матрицах А13 и Л31 было больше нулевых элементов, можно добиться, чтобы коэффициент оптимальности 5 — 7 был ближе к 1.