Справедливые раскраски гиперграфов с ограниченными степенями вершин
Автор: Ширгазина И. Р.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Математика
Статья в выпуске: 2 (58) т.15, 2023 года.
Бесплатный доступ
В статье изучается задача о справедливых раскрасках однородных гиперграфов с ограничением на максимальную степень вершины. Пусть H = (V, Е) - гиперграф, раскраска в r цветов множества вершин V называется справедливой, если в ней каждое ребро из E не является одноцветным, а также мощности любых двух цветовых классов отличаются не более чем на единицу. В данной работе получено улучшение оценки максимальной степени вершины k-однородного гиперграфа, гарантирующей наличие справедливой раскраски в r > 2 цветов при достаточно большом числе вершин.
Гиперграфы, раскраски гиперграфов, справедливые раскраски, вероятностный метод
Короткий адрес: https://sciup.org/142238159
IDR: 142238159 | УДК: 519.174,
Текст научной статьи Справедливые раскраски гиперграфов с ограниченными степенями вершин
Данная работа посвящена задаче о справедливых раскрасках однородных гиперграфов. Начнем с некоторых основных определений из дискретной математики.
1.1. Основные определения
Гиперграфом называется пара множеств Н = (V, Е), где V = V (Н ) есть некоторое конечное множество, называемое множеством вершин гиперграфа, а Е = Е(Н ) есть совокупность подмножеств множества V, и эти подмножества называются ребрами гиперграфа. Гиперграф называется k-однородным, если каждое его ребро содержит ровно к вершин, т.е. является /-подмножеством. Степенью вершины и в гиперграфе Н называется количество ребер этого гиперграфа, содержащих и. Максимальную степень вершины в гиперграфе Н мы будем обозначать через А(Н).
«Московский физико-технический институт (национальный исследовательский университет)», 2023
Раскраска множества вершин V гиперграфа Н = (V, Е) называется правильной, если в этой раскраске все ребра из Е не являются одноцветными. Справедливая раскраска в г цветов — это правильная раскраска вершин гиперграфа в г цветов, в которой все цветовые классы (то есть подмножества вершин, которым присвоен один и тот же цвет) имеют мощности, отличающиеся не более чем на 1, т.е. если Vi,...,V — это цветовые классы раскраски, то должно быть выполнено
||V)| — | V'|| ^ 1 для любых г, j = 1,..., г.
1.2. История задачи
Одно из базовых утверждений теории графов, которое связывает возможность раскраски с максимальной степенью вершины, утверждает, что для любого графа G с максимальной степенью вершины A(G) существует правильная раскраска в A(G) + 1 цвет. В 1970 году Хайнал и Семереди [1] доказали фундаментальную теорему, которая утверждает, что для любого графа G существует и справедливая раскраска в A(G) + 1 цвет. Данный результат положил начало целому ряду направлений в экстремальной комбинаторике, одно из которых связано с получением аналогичных результатов для однородных гиперграфов.
Первым результатом в теории гиперграфов, который связывает возможность раскраски в заданное число вершин с максимальной степенью вершины, была известная теорема Эрдеша и Ловаса [2] 1973 года, которая утверждает, что если Н — это к-однородный гиперграф и
А(Н) ^ , (1)
ек то Н допускает правильную раскраску в г цветов. В дальнейшем оценка (1) неоднократно улучшалась. Здесь стоит отметить работы Радхакришнана и Сринивасана [3], Плухара [4], Косточки, Кумбхата и Рёдля [5], Шабанова [6], Черкашина и Козика [7], Акользина и Шабанова [8]. Наилучшие результаты были достигнуты в [3] (при г = 2), в [7] (для г > 2, но г отпосителыю невелико по отношению к Е и в [8] (г велико по отношению к кй Объединяя их, можно заключить, что если Н — это к-однородный гиперграф и
А(Н) < с (А) ^ гА, у ln к к где с > 0 — некоторая абсолютная константа, то существует правильная раскраска Н в г цветов. Обсуждение точности полученных оценок можно найти в [8].
Справедливые раскраски гиперграфов изучены заметно хуже. С помощью общей теоремы об упаковках гиперграфов из работы Лу и Секеи [9] можно вывести следующий аналог описанной выше оценки (1) Эрдеша Ловаса на случай справедливых раскрасок.
Теорема 1. (Лу, Секеи, [9]) Если Н — это к-однородный гиперграф на п вершинах, г In и
А(Н ) < гА, (3)
2ек то Н допускает справедливую раскраску в г увстов.
Тем самым достаточно лишь в два раза усилить условие на максимальную степень вершины по сравнению с (1) и можно установить не только наличие правильной раскраски в г цветов, но и сделать ее справедливой.
Результат (3) был улучшен для случая двух цветов в работе Шабанова [10] 2015 года, где было показано, что при большом числе вершин любой к-однородный гиперграф Н с условием
9 к— 1
А(Н) ^ с • , (4)
тйпг где с > 0 — некоторая абсолютная константа, обладает правильной раскраской в 2 цвета. Отметим, что результат (4) с точностью до константы совпадает с оценкой (2). При г > 2 наилучшим оставался результат (3).
В заключение отметим еще некоторые работы по справедливым раскраскам гипергра-фов. В работах [И] и [12] рассматривались подобные задачи для подкласса простых гипер-графов, а в недавних работах Ахмеджановой и Шабанова [13], [14] были получены достаточные условия наличия справедливой раскраски в терминах ограничений на число ребер гиперграфа.
1.3. Новый результат
Целью настоящей работы было улучшение оценки (3) в общем случае, для г > 2. Основной результат получен в следующей теореме.
Теорема 2. Пусть Н = (У,Е~) — к—однородный гиперграф, |У| = п, г|п, к > 4, г > 2. Существует такая абсолютная константа с > 0, что если
_ к—1
Д(Н) ^ с • (5)
V к и |У(Н)| > гзкк3, то для Н суищствуст справедливая раскраска в г цветов.
Отметим, что полученная нами оценка несколько слабее результата (2), но и раскраску мы ищем более сильную. Улучшение же по сравнению с (3) очевидно. В следующем разделе мы докажем теорему 2.
2. Доказательство теоремы
Здесь мы следуем идеям из работ [6] и [10]. План доказательства будет следующим. Сначала мы раскрасим вершины гиперграфа Н случайным образом, но так, чтобы цветовые классы были равны по мощности, а далее воспользуемся методом случайной перекраски для того, чтобы исправить одноцветные ребра в получившейся случайной раскраске. Однако при перекраске вершин мы будем сохранять баланс цветовых классов, чтобы после каждого шага перекраски раскраска оставалась сбалансированной.
2.1. Построение случайной биекции
Введем множество W с условием, что |W| = |У|. Разобьем множество |W| на г «цветовых классов» Wi,..., W,, так, чтобы Vг, j € 1,... ,г : |Wi| = \Wj | = п/г. Раскрасим каждое из данных подмножеств в соответствующий цвет, т.е. все элементы Wi будут раскрашены в цвет г. Занумеруем все элементы внутри Wi числа ми от 1 до n/г, Wi = (w1,..., w"/r). Далее, определим связанные элементы следующим образом: зададим г фиксированных биекций fi : Wi ^ Wi+i для г € 1,...,г (подмножество W, будет отображаться в подмножество Wi) по правилу fi(wi ) = w^+1. Назовем группой связанных элементов все подгруппы (в случае, если г делится нацело на 3) из трех элементов вида
(wi, wi+i, wi+2 ), j = 1,...,п/г, г = 1 mod (3), г ^ г/3.
Если остаток от деления г на 3 равен 1 или 2, то добавим к последним группам связанных еще один или два элемента, (w3r-2-cl, w^-1-a, ..., w,), г = a mod (3). Подобные группы также будем называть связанными. И соответствующие группы цветов {1, 2, 3}, {4, 5, 6}, ..., будем называть связанными.
Также рассмотрим на некотором вероятностном пространстве (П, Т , Р ) следующий набор случайных элементов:
-
1) случайную биекцию д : V ^ W с равномерным распределением на множестве всех биекций из V в W. Отображение д порождает свойство связанности на элементы V: вершины V будем называть связонними тогда и только тогда, когда будут связанными их образы в W при данной биекции.
С помощью биекции д мы индуцируем раскраску вершин в исходном множестве V: вершине н сопоставим цвет г Е {1 ...г} о д(н) G W^. Аналогично множеству W, разобьем множество V на (уже случайные) подмножества Vi,..., VT так, что все вершины подмножества V раскрашены в цвет г в изначальной раскраске.
2) Для групп связанных элементов w = (w^',..., w^) (в осн овном, b = 2) введем независимые случайные величины У) с равномерным распределением на отрезке [0,1], не зависящие также от д. Случайную величину Уд будем называть весом каждого из элементов w/,..., w3^. Биекция д индуцирует веса и на множестве вершин гиперграфа: весом вершины н будем называть вес ее образа, д(н). Вее вершииы н будем обозначать через Ху.
2.2. Алгоритм перекраски
Веса задают случайную нумерацию ст связанных групп вершин гиперграфа согласно своему вариационному ряду. Если в ребре нет связанных вершин, то она же естественным образом задаст и нумерацию на вершинах ребра. Отметим, что наличие пары связанных вершин в ребре означает невозможность его одноцветности, так что в потенциально плохих ребрах нумерация будет определена, корректно и веса, будут независимы.
В получившейся изначальной случайной раскраске некоторые ребра, гиперграфа, могли получится одноцветными, укажем алгоритм перекраски для исправления таких ребер.
Перекраска — непрерывный процесс для t Е [0,1], в рамках которого несколько меняется биекция из V в W. Каждая вершина н рассматривается в момент времени своего веса, Ау и для нее проверяются следующие условия.
-
• Вершина н принадлежит одноцветному в момент времени Ау ребру А, которое было одноцветно и в изначальной раскраске.
-
• Вершина н еще не меняла свой цвет.
-
• Вершина н — первая по нумерации ст в ребре А.
Если все перечисленные условия выполнены, то мы меняем цвета у ни всех вершин, связанных ей. Цвета меняются следующим образом.
• Пусть (ні,...,нь) — это группа связанных вершин, в которую входит н. Пусть (с,..., с + b — 1) — это их пана..тьные тщета., а. н = щ.
• Выбираем случайно и равномерно цвет из множества {с,..., с+b —1}\{с+г —1}. Пусть мы выбрали цвет с + h. Присваиваем вершине н цвет с + h, остальным вершинам — по циклу, т.е. вершина ну получает цвет с + (h + j — г mod b).
2.3. Вспомогательные факты
е С формальной точки зрения смена цветов означает частичную смену биекции. Пусть д’ — биекция до момопта рассмотрения н. тогда полагаем д'Чн) := д‘(ні+(һ+^-і modь)), з = 1,...,b, и д‘‘(ш) = д‘(ш) для всех остальных вершин.
Таким образом, в процессе перекраски мощности цветовых классов сохраняются. Для доказательства, теоремы остается показать, что в получившейся финальном раскраске, индуцированной итоговой биекцией /, вероятность наличия одноцветных ребер в гиперграфе меньше единицы.
Перед тем, как начать подробный разбор плохих случаев, приведем несколько вспомогательных технических лемм, которые помогут нам при последующих подсчетах.
Лемма 1. Пусть q,l С п/t, тогда
(n/r),(n/T)i < г-(9+/)е, где (а)ь = а(а — 1)... (а — b + 1).
Доказательство. Для начала покажем, что для любого l С n/3 выполняется неравен ство
C^VdiWdi < — 2 1 (n)2 i С
Действительно,
(n/T) i (n/r^ i = T-2 i П (n — T] )2
(n)2 i T Д (n — 2])(n — (2] + 1))
(^ С 1 Щ>11 r > 2)
С Т-21 П T - 2] < т-21 f1 + ____Y < n — 2] — 1 n — 2(l — 1) — 1
V n/37
Далее, по условию q и l не превосходят n/3. Пусть без ограничения общности l С q С n/3. Тогда получим
(п/t) , (n/r) i = (п/т) і (п/т) і ( п/t — l) • ... • ( п/t — q + 1) <
(n)q+ i (n)2 i (n — 2l) •... • (n — (q + l) + 1)
< T-21 . -( , - i ) (n — Tl) • ... • (n — r(q +1)) -( , + i )
" e (n — 2l) • ... • (n — (q + l) + 1) < e.
□
Лемма 2. Пусть ж + у + г < 3k т г ^ 3, тогда
(nM ^ (nM y (nM ^ < 2 • т-(ж+ ^ +г) ( п ) ж + У + 2
.
Доказательство. Без ограничения общности можно считать, что г ^ у ^ жиг С n/3.
Тогда
(п/гМп/гЫп/ТІ £ = T-( ^ + y + ^ )n3 тт1_____________ (n — Т])3 _____________
(n) x + y + z 1=1 (n — 3] + 3)(n — 3] + 2)(n — 3] + 1)
'У - 1
x П
1 = ж
(n — г])2
(n — ж — 2] + 3)(n — ж — 2] + 2)
z -1
• П j=y
n — T]
n — ж — у — ] + 3
x+ry + z x П j=x+y+z-2
(n — ] + 1).
В вышеприведенном выражении мы считаем, что второе произведение в правой части равно 1, если ж = у, а третье равно 1, если у = г. Заметим, что каждый множитель в первых трех произведениях не превосходит 1:
(п — Г] )3
< 1
при ] С ж — 1;
(п - 3] + 3)(п - 3] + 2)(п - 3] + 1)
(п — г]) 2
--------- --------.)..,, < 1 пРп] Е [ж,у -1];
(п -ж - 2] + 3)(п - ж - 2] + 2)
п - г] ------------—— < 1 при ] Е \у,г - 1]. п -ж -у -]+ 3
Таким образом,
(п/3Ып/3)У(п/3Д < __________ п3 __________ • г-(ж+у+г) < 2r-(x+y+z)
(п)х+у+г (п - (ж + у + г) + 1)3
в силу того, что п > г3кк3 очень велико по отношению к к и ж + у + г С 3к. □
Заметим, что описанное в условии леммы 2 неравенство естественным образом распространяется и на случай четырех множителей в числителе.
Лемма 3. Пусть ж + у + г + t С 3к, 1 С b С 3, г ^ max(b + 1, 3) — натуральные числа, тогда
(п/Г)х(п/Г)у (п/гк (Ьп/г) ~ , t У+y + z )
< 2 • b • Г .
Wz+y+z+t
Доказательство. Доказательство проводится тем же способом, что и в предыдущей лемме.
□
Далее, нам будет нужна Локальная лемма для случая отрицательно коррелированных событий. Доказательство леммы в общем параметрическом случае можно найти в главе 5 книги [15], а соответствующий подбор параметров — в работе [16].
Лемма 4. Пусть А 1 ,..., Ам — события на некотором вероятностном пространстве. Пусть для каждого события Аг выделено некоторое конечное множество dom(Aг ) с таким условием, что для любого J С {] : dom(Aj ) П dom(Aг) = 0} выполнено
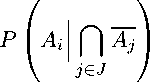
СР (Аг) .
Обозначим через DOM = U M 1 dom^) и для каждого и Е DOM введем следующий полином:
ш. (г) = ^ Р (Аг) Aom(A ) |.
i:nEdom(Ai)
Если существует такой полином ш (г) с условием ш (г) ^ шу (г) для любыж и Е DOM и г ^ 1, а такэісс у Е (0,1), такое, что ш (1/ (1 - у)) С у, іио
Р (ЙАг)
> 0 .
Также нам потребуется теорема Лу и Секеи [9] об отрицательных корреляциях в пространстве случайных биекций. Пусть U, Ү — два конечных множества одинаковой мощности, а ж — случайная биекция из U в Ү, имеющая равномерное распределение. Для любых подмножеств S С U, Т С У, |S| = |Т|, и фиксироваиной биекции у : S ^ Т , назовем каноническим событием
A(S, Т, у) = {т(v) = у(v) для лтобого v G S}.
Канонические события A(S, Т, у) и A(S', Т‘, у') конфликтуют (в терминологии Лу и Секеи), если:
1) существует v G S П S 'с условием у (v) = у'(v) или
2) существует 5 G Т П Т' с условием у-1 (J) = (у')-1 (5).
2.4. Разбор плохих случаев
т.е. если f и f' нельзя совместить в единую бпекщіто между S U S' іі Т U Т '.
Теорема 3. (Лу, Секеи, [9]) Для любых канонических событий A и B1, ..., Bs, попарно не конфликтующих с A, выполнено отношение отрицательной корреляции:
(S a| Q Bj I 3=1 Рассмотрим все плохие события, когда в финальной раскраске, индуцированной итоговой биекцией f. остались одноцветные ребра. Заметим, что если ребро А оказалось одноцветным цвета а в финальной раскраске, то оно не могло быть одноцветным цвета а в начальной раскраске, так как для вершины ребра А с наименьшим номером автоматически выполняется условие перекраски. Значит, если ребро стало одноцветным цвета а в финальной раскраске, то некоторые его вершины изначально были окрашены в другие цвета и перекрасились в процессе перекраски. При этом данные цвета обязаны быть связанными к цвету а, иначе перекраска в а невозможна, т.е. изначально в А могли быть вершины цветов из весьма ограниченного множества. Далее, каждая вершина могла перекраситься либо потому что условие перекраски выполнялось для нее самой, либо потому что условие перекраски выполнялось для какой-то связанной с ней вершины. Для каждого изначально присутствующего в ребре А цвета 3 = а мы будем рассматривать вершину v. последнюю сменившую цвет с 3 па а. Если условие перекраски выполнялось для самой v, то должно было быть ребро В, в котором эта вершина была первой, и которое было одноцветным цвета 3в начальной раскраске. Сразу сформулируем очевидное наблюдение. Утверждение 1. Ребра А и В пересекаются только по вершине v. Доказательство. В момент рассмотрения v вершины В все еще раскрашены в цвет 3. а в ребре А опа. — едиііствеішая оставшаяся вершина, цвета. 3- □ Если же условие перекраски выполнялось для вершины и, свяязанной с v, то мы получаем ребро, которое содержит и и может совершенно по-разному пересекаться с А. Начнем перебор случаев. Для каждого класса, плохих событий мы будем сразу выписывать полином для будущего применения Локальной леммы. Будем суммировать для каждой вершины и гиперграфа Н вероятности событий данного типа, в которых она участвует. В качестве параметра у удобно будет брать У = к+"1. Параметр dom мы формально опишем позднее, грубо говоря, в него войдут участвующие вершины гиперграфа, а также их образы при отображении д. В качестве оценки его мощности будем брать удвоенное число участвующих вершин. Случай 1 Ребро А стало одноцветным цвета а в финальной раскраске, при этом изначально в нем были только вершины цветов а и 3, а «1 - последняя из перекрасившихся вершин цвета 3, поменяла свой цвет, так как сама удовлетворяла условию перекраски. В силу того, что для вершины «1 выполнялось условие перекраски, значит, она была первой в некотором одноцветном ребре By. В силу утверждения 1 ребра А и B1 пересекаются только по вершине «1. Пусть также еще I — 1 вершин ребра А перекрасились из 3 в а до этого момента, значит, их вес должен быть меньше, чем у вершины «1, и при случайном выборе цвета перекраски должен был выпасть а. Эти вершины мы можем выбрать ^-1) способам и в ребре А, вершина «1 определяется однозначно из пересечения А и B1. Оставшиеся вершины ребра B1, наоборот, имеют но мер больший, чем у «1, и все изначально имеют цвет 3- Также заметим, что у нас есть г способов для выбора а финального цвета ребра А. Также обозначим (здесь и далее) через а = а(а) — количество способов для выбора связанного цвета в данной подгруппе цветов (задается выбором а). Для большинства значений а, а(а) = 2. Обозначим подобное событие через ДДА, B1) и оценим его вероятность: Р (Л1(А,BY)) ^ Е Е Q- 1)а(а) -^ 1 ■ . / x) (^)2к-1 \а(а) 1-1 1 а(а) • (1 — х)к 1dx ^ (воспользуемся леммой 1) т к < ЕЕ г1-2к - (к—1) 1 а(а)/-1 (1 — х)к 1dx т к = ЕЕ -^ • ------;— • е. а(а)1-1 (к ~ 1)! (к - 1)!(1 - 1)! (к - 1)!(- — 1)! (к + I - 1)! Оценим отношение факториалов. При I = 1 оно равно 1/к, иначе (к — 1)!(к — 1)! (к — -)!(к + I — 1)! (к — I + 1) •... • (к — 2) • (к — 1) к •... • (к + I - 2) • (к + I - 1) 1 (к — I + 1) • ... • (к — 2) • (к — 1) 1 к (к + 1) • ... • (к + I — 2) • (к + I — 1) < к Подставив полученную оценку в выражение для вероятности исходного события, получим т к Р(Л1(А,B1)) < ЕЕг1-2к а=11=1 • е • 1 < а(а)1 1к (пользуемся тем, что а(а) 3 2) к 1 ^ г2-2к.Е 2/-1 1=1 • е • - < к 2е • г2-2к 1. к Оценим локальный полином для описанного типа событий в точке у = 1/(1—у) = 1+1/к. Для любой вершины n Е V оценим число способов зафиксировать конфигурацию ребер А и B1, n Е А U B1. Сначала необходимо двумя способами выбрать, какому из двух ребер принадлежит данная вершина, А(Н) способами выбрать данное ребро, к способами выбрать, по какой вершине заданное ребро пересекается со вторым и А(Н) способами задать оставшееся ребро: Сб^ Е р(а,(а,в,)) • іЩ^с Е --2к+2 • 2 • =16 +1) (A,Bi):uEAUBi (A,BiYuEAUBi Х 2 4к ⩽ < 2е • А(Н) • к • А(Н) • --2к+2 • 2 • е1 f 1 + 1) < 4А(Н)2 • - к \ к J (используем оценку (5): А(Н) < сгк-1к-1/2) 2к+2 ^=5 < < 4 • с2 - . 2к—2 к • - 2к+2 =5 = 4с2е5< А к 20 для достаточно малой константы с > 0. Случай 2 Ребро А стало одноцветным цвета а в финальной раскраске, при этом изначально в нем были только вершины цветов а и 3. и последняя из этих перекрасившихся вершин v, поменяла свой цвет, так как условию перекраски удовлетворяла одна из связанных к v, вершин — вершина п,. При этом п, принадлежала одноцветному ребру В, цвета а, и ребро В, пересекается с ребром А. Заметим, что в данном случае ребро В,, содержащее вершину п,, может пересекаться с ребром А по нескольким вершинам начального тщета а. При этом сама, вершина, п, не может принадлежать ребру А, так как иначе ребро А не могло бы стать одноцветным. Обозначим через Т количество вершин в пересечении А и В,. Снова, вершина п, должна быть первой в ребре В,, а все вершины изначального цвета 3 в А должны иметь вес, меньший чем вес v, (который равен весу п,), поэтому среди них нет связанных вершин к вершинам В,. Кроме того, вглорав значение д(п,) и тщета, а. 3-мы автоматически выбираем и g(v,). т.к. они обязаны быть связанными. Обозначив данное событие через А2(А, В,), оценим его вероятность: ̃︀ х^—1 а1 (а) (1 — х)к ,dx = Р АА В,)) < ЕЕ “(а) • (" — ') • (к - Т • I I" (7\3(7 )'-1 а=Х 1=, \ 1 / Vo (П)2к—1 т k—l = ЕЕ а=,l=, ( 7) 2к—,—?•(?), (п)2к—Т П — -Т ︀ к.к—1 • (к — I) • Т • , .,—1 [ xl 1 • (1 — х)к , dx < а(а)1 1 0о (пользуемся тем, что ^^ < 27’ и применяем лемму 2) т к—l < ЕЕ-—2к+‘ • а=,l=, 2- П 1 • , • (к — Т)(к — ^)!(к — 1)!(/ — 1)! а(а)1—, Д!(к — Т — Г)!(к + I — 1)! ‘ Оценим последнюю дробь следующим образом: (к — Т)!(к — 1)!(Т — 1)! 1 И(к — Т — 1)!(к + I — 1)! 7' Подставив данную оценку, получим т к—l 9 _ Р (А2(А, В,)) < ЕЕ -—2к+1 • — • е • , ,,Лк — Т) = -,—2к+1 2—<2—< п а(а)1 , а=,l=, 1 ' 2е(к — Т)хС Ер 1 П J=! l=, а(а)l—, ⩽ (снова пользуемся тем, что а(а) ^ 2 и максимизируем по I А к — 1) ⩽ Мк—Цт2-2к+1 ^ 4£т3-к п п По аналогии с предыдущим случаем оценим локальный полином. Здесь при оценке числа конфигураций мы действуем точно так же, ведь ребра снова пересекаются: ■ С £ Р (^2(^,В1У) • (у)2|АиВ1| ^ £ 4ет3-к Л + к\^ (A,Bi):uEAUBi (A,Bi):uEAUBi а2 ^ 2 • А(Н) • к • А(Н) • —т3-к • е4 ^ 8е5 • (А(Н))2 к • т3 к ^ пп ^ 8е5с2 • т + к ^ ^(9) п 20 в силу начального условия п 3 тзкк3. Случай 3 Ребро А стало одноцветным цвета а в финальной раскраске, a vi — последняя из перекрасившихся вершин цвета 3, поменяла свой цвет, так как условию перекраски удовлетворяла одна из связанных vi вершин — вершина щ. При этом щ принадлежит одноцветному ребру Bi цвета. а. и ребро Bi не пересекается с ребром А. Данный случай с точки зрения оценки вероятности полностью аналогичен предыдущему, только теперь I = 0, оптимизировать по нему не нужно. Получим Р(A3(A,Bi)) ^ — п т2-2. Оценим локальный полином для данного типа событий. Сначала А(Н) способами выберем ребро, которому принадлежит вершина и. Далее, так как ребра не пересекаются, то второе ребро мы просто выбираем не более чем |S| ^ пА(Н)/к способами. В итоге -4 ® = Е Р1)) • ®2|AuB‘I (A,Bi):mGAUBi ⩽ Е (A,Bi):uEAUBi 4ке • т2-2к п (і+к )4к ⩽ ^ 2А(Н) • п • А(Н) • Ы •< к п ^ 8е5 • (А(Н))2 • т2^2 < 8е5с2• г2-2к = 8с^е5 ^(10) кк для достаточно малой константы с > 0. Случай 4 Ребро А стало одноцветным цвета а в финальной раскраске, при этом изначально в нем были только вершины цветов а и 3, и последняя из этих перекрасившихся вершин vi поменяла свой пвет. так как условию персжраски удовлетворяла одна из связаішвіх vi вершин — вершина ui. При этом ui принадлежит одноцветному ребру Bi цвета у, отличного от а п 3- Заметим, что в данном случае ребро Bi не могло пересекаться с ребром А, так как в ребре А в изначальной раскраске не было вершин цвета у. Здесь все почти аналогично предыдущему случаю, но у нас есть изначально вершины трех различных цветов, снова нет других пар связанных вершин, кроме П1 и щ, среди цветов 3 и 7- Получаем Р (А4(А,ВіУ) * е е С) =1 — •к • I • а(а) • (а(а) — 1) х 1 ("к-ДУШ--! ( * V-1 1.к-1. х./охл(1 "^* (воспользуемся леммой 2) * £ £ 2г1-а---• (к) • к • I • («(а) — 1) • 3 ()11 (1 — Щ-14т * t—11—1 П -2к + 1 1 о г к ⩽∑︁∑︁ 4ЫО(а) — 1)1-2к АА У - 1)!(к — 1)! п(а(а))1-1 Д (к +I — 1)! ⩽ г к ⩽ ЕЕ а—11—1 4к(а(а) — 1) п(а(а))1-1 т1-2к ⩽ (пользуемся тем, что 2 * а(а) * 4) * 24кт2-2к П . Оценим локальный полином для данного типа событий. Заметим, что сама конфигурация данного случая совпадает с конфигурацией из предыдущего случая, у нас просто два непересекающихся ребра. Таким образом, получаем 44)(у) = Е Р (^4(А,В1)) • (y)2^UB1| (A,Bi):uEAUBi ⩽ Е (A,Bi):uEAUBi 24 к • т2-2к П (1+к )4к ⩽ * 2А(Я) • П • А(Я> • • Г2-2к * к п * 24е4 • (А(Я))2 • т2-2к * 24е4с2• т2-2к = 2^4 * (11) к к 20 для достаточно малой константы с > 0. Остается разобрать случаи, когда в ребре А в начальной раскраске есть как минимум два других цвета, помимо финального цвета а. Пусть щ — последняя вершина, сменившая цвет на а, имеет начальный цвет 3, а вершина щ — последняя вершина, сменившая цвет на а, чей начальный цвет был не равен 3- Снова каждой из двух вершин соответствуют изначально одноцветные ребра В1 и В2, которые либо содержали щ и щ соответственно, либо содержали связанные к ним вершины. Трудность в рассмотрении данной конфигурации состоит в том, что в ребрах В1 и В2 уже могут появляться другие пары связанных вершин, веса которых являются зависимыми. Также сделаем простое наблюдение, которое показывает, что в случае перекраски из-за самих щ и щ мы имеем дело с древесной конфигурацией. Утверждение 2. В этом случае выполнено АПВ1 = {щ}, АПВ2 = {v2} и В1 ПВ2 = 0. Доказательство. В момент рассмотрения щ вершины В2 все еще раскрашены в некоторый цвет 7 = 3- а в ребре А она. едшіствешіая оставшаяся тщета, не а и нс 3- В момент рассмотрения V1 вершины В2 все еще раскрашены в цвет 3, а в ребре А она единственная оставшаяся цвета не а. Ребра В1 и В2 не пересекаются, т.к. их вершины имеют разные цвета в начальной раскраске. □ Случай 5 Ребро А стало одноцветным цвета а в финальной раскраске, при этом изначально в нем были вершины еще как минимум двух цветов. Пусть 3 — последний пропавший цвет, vi — последняя вершина цвета 3, перекрасившаяся в а. Пусть у — предпоследний пропавший цвет, V2 — последняя вершина цвета у, перекрасившаяся в а. Пусть вершины vi и V2 перекрасились, так как сами удовлетворяли условию перекраски, из-за ребер Bi и В2. Есть две принципиальные ситуации. Либо среди вершин В2 и вершин начального цвета 3 в А U Bi есть пара связанных вершин, либо такой пары нет. Рассмотрим сначала вторую ситуацию. Здесь все очень похоже на случай 1. Пусть l — число вершин начального цвета 3 в А, а т — число вершин начального цвета не а и не 3 в А. Тогда ребро Bi изначально полностью имеет цвет 3, vi — первая вершина Bi. Вершины же начального цвета 3 в А, наоборот, имеют веса меньше веса vi, и они должны перекраситься в а. Ребро В2 изначально имеет цвет у, V2 — первая вершина В2, все вершины начального цвета не 3 и не а в А имеют веса меньше веса V2 и они должны перекраситься в а. Обозначим описанное событие через Д^^А, Bi, В2) и оценим его вероятность: Р(Д^(А, Bi,B2)) У £ У У (^ - f)^ t"1 ') • °(а) • («(а) - 1) х a=i l=i m=i ЙУ—Дкi^^ (n)3k—2 X Io («(а)) (1 x)‘ i«(а)dx / (Да)) (1 У)‘1«(а)dy У (воспользуемся леммой 3) У ЕЕ Е22т—3к+2(«(а) - '- f)^-Д)х а=1 l=i m=i х Г Л1 - y)k—i(1 - x)k—1 ()m i • () i dydx = J 0 Jo V «(а) / \°(а)/ (суммируем по т под знаком интеграла) г k—i = ЕЕ2г a=il=i —3k+2 (--- 2)'/7oi(1 - s)k—i(1 - z)k—i ( , ма -1))k—1—i A1+ «(а) ) («(а)l—i dydx = (суммируем по l под знаком интеграла) = Е 2^—3k+2 ■ Oi j> - y)‘—i(1 - x)k—i(1 + ") + «X))‘—2dydx< ^ У 2т—3k+2 • 3 A e— (пользуемся тем, что «(а) 3 2) V"^- і"1 і"1—(^-ЛСу+т) У 2т 3 + • у У e “(a)dydx У ⩽ Е 2г- 3к+2 —(һ-ІДу + ж) е а(“) dydx = = Е 2г-3к+2 (^V С 64 • г3-3к, а=і ' где мы воспользовались тем, что а(а) С 4. Теперь рассмотрим ситуацию, когда все-таки имеется пара связанных вершин в конфигурации. Здесь мы проигнорируем веса вершин в принципе, а только оценим вероятность того, что каждая вершина ребра А либо имела цвет а изначально, либо его не имела, но ей выпал при перекраске цвет а, каждая вершина из Ві ил и В2 получила изначально цвет этого ребра, и, наконец, некоторая вершина из В2 оказалась связанной к какой-то вершине из А U Ві. Обозначим описан ное событие через ДІ^А, Ві ,В2^ и оценим его вероятность. Пусть I — это число вершин А, покрашенных в цвет не а изначально, тогда при выбранных связанных вершинах образ д для обоих однозначно определяется выбором образа для одной вершины Р ^(ДВ^У) с ее А 22) = 1 • а(а) • (а(а) — 1) х х ( («(а) Е-2 (п)3к—2 г • к•2к • — п • На))/ (воспользуемся леммой 2) (к — 2Х _ 2кк2 I — 2/ п • г4-3к. 2к2гк—2 3&+2 С---- > > 2г-3к+2 п ^—' ^—' В силу условия на п данное выражение меньше, чем г3 3кк2, поэтому для объединенного Д5(А, Ві, В2) = дА(А, Ві, В2) U Д^Ча, Ві, В2) выполнено Р(Д5(А, Ві, В2)) С 65 • г3-3кк-2. Оценим локальный полином для описанного типа событий в точке у. Заметим, что для того, чтобы зафиксировать данную конфигурацию из ребер А, Ві и В2 для фиксированной вершины, необходимо тремя способами выбрать, какому из трех ребер принадлежит данная вершина, А(Н) способами выбрать данное ребро, к способами выбрать, по какой вершине заданное ребро пересекается с ребром Ві и А(Н) способами задать В^ за тем к способами выбрать, по какой вершине первое выбранное ребро пересекается с ребром В2 и А(Н) способами задать В2: 45)(у) = Е Р (Дб(А,Ві,В2)) • (у)2|АиВ1иВ2| С (А,В1,В2):mG^UBiUB2 1 X 6к С Е 65 • г3-3кк-2 (1 + Ы С (А,В1,В2):меАиВ1 ив2 2 С 3 • А(Н) • к2 • (А(Н))2 • 65 • г3-3кк-2е6 С (подставляем оценку А(Н)) 3к—3 < 195е6с3----- С ° к3/2 • г-3к+3 = 195е6с3к-3/2 С — для достаточно малой константы с > 0. Случай 6 Ребро А стало одноцветным цвета а в финальной раскраске, при этом изначально в нем были вершины как минимум еще двух цветов. Пусть 3 — последний пропавший цвет, vi — последняя вершина цвета 3, перекрасившаяся в а. Пусть у — предпоследний пропавший цвет, V2 — последняя вершина цвета у, перекрасившаяся в а. Пусть вершины vi и V2 перекрасились, так как одна из них сама удовлетворяла условию перекраски, а вторая — из-за того, что условию перекраски удовлетворяла одна из связанных ей вершин. При этом ребро, содержавшее эту связанную вершину, не пересекалось ни с ребром А, ни со вторым ребром. Ситуация с ребрами почти симметричная, поэтому рассмотрим только ситуацию, когда вершина V2 удовлетворяет условию не рекраски сама, а вершина vi перекрашивается из-за связанной. Все полученные оценки будут верны, поэтому мы будем ставить коэффициент 2 при подсчете полинома. Пусть в ребре А изначально было q вершин цвета а, І вершин цвета /3, 7 вершин цвета у и s вершин оставшихся связанных цветов из данной подгруппы (напомним, что в теории у нас может быть до 5 цветов в группе). Заметим, что в данном случае вершина V2 задается из пересечения ребра А с ребром B2, а выбрать вершину vi мы можем І способами (и к способами выбрать связанную ей в ребре Bi). Как и ранее, нам необходимо задать цвета 3 и у, но заметим, что ребро Bi может иметь произвольный начальный цвет из выбранной группы цветов. Как и в предыдущем случае, рассмотрим отдельно два варианта: когда среди вершин В2 и вершин начального цвета 3 в А U Bi есть пара связанных вершин либо такой пары нет. Рассмотрим сначала вторую ситуацию и обозначим подобное событие через Л^А, Bi, B2)). Учитывая неопределенность с цветом вершин Bi. получаем Р(Л^А. Bi, B2))) С — — —^„ • („(а) - 1) • (к- ЗЗ; І)(к - 7 -1) •к • ІХ '=i l=i m=i s=0 / \ / \/ (7X-l-m-s(.7)/-l(7L+x '2 , °) (7ki 1 o 1 ‘mV ** x -X (n)3k—i X IiГ ("ТУ V (1 - y)k-i • () (1 - x)k—i'-У-Х С J0 ./0 а(а) а(а) а(а) а(а) (пользуемся леммой 3) т k—i С — — 2т—3k+i•к • '=ii=i (к -1) X Е <к; ^ 33 Г m=i \ 7 / \„(а) / — • а2(а) • (а(а) — 1) • ( ) • I / (1 - у)к i(1 - x)k i x п а(а)/ ,/о ./о (Г-е* (к - 7-1)(„3))' (“(“) - 2)1* С С ЕЕ 4г-3к+ь(к - 1) •кПТ-(а) - 1)x '=i l= X (1 -У) k—i(1 - x)k—i („7))M x-1 (к - І) (у)m—i ,^i 7 а(а) X X (1+ У(„(а) - 2))k-m—l а(а) т dydx С — 4r—3k+2 '=i k - •(а(а) - 1)x п х f f J 0 Jo к-1(1 - x)k-1Е«С -1)( ^ )w(i + ^) k-l dydx ^ ^ Е 4г-3к+2 • - («(а) - 1) Г Л1 - y)k-1(1 - x)k-1(1 + 4- + E(.MJ2) 1dydx ^ t=1 n Jo Jo V °(a) °(a) J T ^ Е 4г -3k+2 ' /e- (k-1>»+(k-1>-(^e-<k-1).+(k-l)^dydx< T ^ V 4г—3к+2 1 Г1 —(У—1)(у+У) ' / е- ДЮ dydx< T ^ Е 4г 3k+2 • ” w“) -1) () n у к - 1 ) ⩽ (пользуемся тем, что q(q) ^ 4) < 192г-3к+3 — • 1 < З84т-3к+3 • 1 п (к - 1)2< п Теперь рассмотрим ситуацию, когда в конфигурации есть пара связанных вершин. Аналогично случаю 5 мы проигнорируем веса вершин, а только оценим вероятность того, что каждая вершина ребра А либо имела цвет а изначально, либо его не имела, но ей выпал при перекраске цвет а, каждая вершина из В1 ил и В2 получила изначально цвет этого ребра, некоторая вершина В1 оказалась связаиной вершине из А, и, наконец, некоторая вершина В2 оказалось связанной к объединению вершин ребер А и В1. Заметим, что эта вершина должна быть отлична от вершины, связанной к гц в ребре В1. Обозначим описанное событие через д62)(А, В1, В2) и оценим его вероятность. Пусть I — это число вершин А, покрашенных в цвет не а изначально. Вспомним также, что для выбранной пары связанных вершинах и выбранных цветов ребер В1, В2, об раз д почти однозначно определяется выбором образа лишь для одной вершины в паре. Р(Д»'(а.В1.В2 )) < 2£ £ (к - 3 • a(a)(a(a + 1)) • к2 • к • 2кх а=1 l=1 х(тУЛГШк Н“) 7)1-1• / г <2 • 1 < (n)3k-1 зп («(а))1 (воспользуемся леммой 3) < ' . ' Е «(") і: 2г-3к+1(к - 11) « 3^^ • г4-3к. а=1 l=1 В силу условия на п данное выражение меньше, чем г3 3kп 1, поэтому для объединенного события Р(Ме(А, В1, В2)) = Р(А^(А, В1, В2)) U Р(а62(А, В1, В2)) выполнено Р(Ме(А,В1,В2)) ^ 385г-3к+3 • 1. п Оценим локальный полином для описанного типа событий в точке у. Заметим, что для того, чтобы зафиксировать данную конфигурацию из ребер А, В1 и В2 для фиксированной вершины, необходимо тремя способами выбрать, какому из трех ребер принадлежит данная вершина, А(Н) способами выбрать данное ребро, к способами выбрать, по какой вершине заданное ребро пересекается с ребром В2, А(Н) способами вьібрать ребро В2, ребро В1 просто выберем всеми возможными способами. И не забудем обратную ситуацию, когда В^ не пересекается с И. В итоге получим Осталось рассмотреть случаи, когда обе вершины vi и V2 в Ребре А перекрашиваются из-за связанных с ними вершин в ребрах Ві и В2. Здесь возможны разные варианты пересечения ребер, а также проблемы возникновения дополнительных связанных пар вершин. Сначала рассмотрим ситуацию, когда одно из ребер Ві и В2 пересекается с А. Случай 7 Ребро А стало одноцветным цвета а в финальной раскраске, в нем изначально был цвет 3, и последняя из перекрасившихся вершин цвета перекрасилась, так как условию перекраски удовлетворяла одна из связанных ей вершин в одноцветном ребре В. При этом ребро В пересекается с ребром А. Оценим вероятность искомого события. Каждая вершина В должна иметь некоторый один и тот же цвет у, не совпадающий с 3. в начальной раскраске, при этом его первая вершина v не должна принадлежать А, но должна быть связанной с одной из вершин цвета 3 в А \ В. Далее, все вершины в А \ Ві должны были получить изначально либо а, либо один из цветов, связанных с ним, а затем перекраситься в цвет а (отметим, что выбор цвета перекраски для них будет независимым). Обозначив через I мощность пересечения А и В, мы получим следующую оценку данного события ДДА, В): ~ тэг л г л А - Л (n/r)s(n/r)k(а(а)п/т) В(Л7(А, В)) ^ ^(а(а) + 1)^2^ ( „ ) а=1 s=G 2 7 7 k—l—s (n)2k-l 7 7 г • (—У ^ п а(а)) (пользуемся леммой 3) ^ 8r2 2k(2T)k321. п ^ \ (а(а) + 1)к2 • 2rl-2k2k-1-п ^=1 Теперь посчитаем локальный полином для этого типа события. Заметим, что для того, чтобы зафиксировать данную конфигурацию из ребер А и В для фиксированной вершины, необходимо двумя способами выбрать, какому из двух ребер принадлежит данная вершина, А(Н) способами выбрать данное ребро, к способами выбрать одну из вершин в пересечении и А(Н) способами выбрать ребро, которому принадлежит эта вершина: -(Д = £ В (Л7(А, В)) • (y)2|AUB| (A,B)vuEAUB ⩽ Е Sr2-2k(2r)kк21 (A,B):yGAUB (1+к Г ⩽ ^ 2А(Н)2к • 8e4r2-2k(2r)kк21 ^ 16е4с2 • (2r)kк21 ^ п п (пользуемся тем, что п 3 к3гзк^ / 16е4с2 у ^ к < 20 для достаточно малой константы с. Очень похожим образом разбирается следующий случай, когда ребра не пересекаются. Случай 8 Ребро А стало одноцветным цвета а в финальной раскраске, при этом изначально в нем были вершины как минимум еще двух цветов. Пусть 3 — последний пропавший цвет, Hi — последняя вершина цвета 3, перекрасившаяся в а. Пусть у — предпоследний пропавший цвет. V2 — последняя вершина тщета у. перекрасившаяся в а. Пусть вершины Hi 11 V2 перекрасились, так как одна из них сама удовлетворяла условию перекраски, а вторая — из-за того, что условию перекраски удовлетворяла одна из связанных ей вершин. При этом ребро, содержавшее эту связанную вершину не пересекается с ребром А, но пересекается со вторым ребром. Без ограничения общности будем считать, что вершина Hi перекрасилась из-за ребра Bi, которому она и принадлежала. Как мы помним, тогда |А П Bi| = 1. Пусть вершина V2 перекрасилась из-за ребра B2, которому принадлежала связанная ей вершина, причем ребро B2 пересекается с Bi, но не с А. Оценим вероятность искомого события. Каждая вершина Bi U B2 должна иметь некоторый один и тот же цвет 3. не совпадающий с а. в начальной раскраске. Одна из вершин B2 должна быть связанной с одной из вершин А \ Bi. Далее, все вершины в А \ Bi должны были получить изначально либо а. либо один из цветов, связанных к нему, а затем перекраситься в цвет а (снова выбор цвета перекраски для них будет независимым). Обозначив через I мощность пересечения Bi и B2. мы получим следующую опенку данного события А8(А, Bi, B2Y Р (Л8(А, Bi, B2 V- , „.гД/к - О (п/г),(п/г) )) ЩТ «<а)к2Е ( s ) 2к-М“)п/Г)к-І (п)3к-І-1 . r Д1"' < п уа(а) у (пользуемся леммой 3) Г ^ 8r3+i-3k2кк21 ^ 8r3-3k(2r)kк21. п п ⩽ Е а(а)к2 • 2гІ+Г-3к2к-І Г а=І П Распишем локальный полином для даннного типа событий в точке у. Заметим, что для того, чтобы зафиксировать данную конфигурацию из ребер А, Bi и B2 для фиксированной вершины, необходимо тремя способами выбрать, какому из трех ребер принадлежит данная вершина, А(Н) способами выбрать данное ребро, к способами выбрать, по какой вершине заданное ребро пересекается с ребром Bi (или А) и А(Н) способами задать его, затем к способами выбрать, по какой вершине ребро Bi пересекается с третьим ребром B2 и А(Н) способами задать его: - у = Е Р (A8((А,Bi,B2)) • (у)21АиВ1иВ21 ^ (A,Bi,B2):dGAUBiUB2 ⩽ Е (A,Bi,B2)vueAuBiUB2 8r3-3k(2г)кк21 п 1Х6к (1+к) ^ 3А(Н)3к2 • 8e6r3-3k(2r)kк21 п ⩽ * 24е6с3 (2г)кк5/2 „ у п < 20 для достаточно малой константы с. Здесь мы снова пользовались тем, что п 3 к3гзк. Остались лишь случаи, когда вершины vi и v2 перекрашиваются из-за связанных, но ребра Bi и В2 не Пересе каются с А. Здесь есть лишь два варианта: Bi и В2 пересекаются между собой или нет. Начнем со случая непустого пересечения, потому что он почти идентичен случаю 8. Случай 9 Ребро А стало одноцветным цвета а в финальной раскраске, при этом изначально в нем были вершины вершины как минимум еще двух цветов. Пусть 3 — последний пропавший цвет, vi — последняя вершина цвета 3, перекрасившаяся в а. Пусть у — предпоследний пропавший цвет, V2 — последняя вершина цвета у, перекрасившаяся в а. Пусть вершины vi и V2 перекрасились в силу того, что условию перекраски удовлетворяли связанные им вершины из ребер Bi и В2, причем эти ребра пересекаются между собой, но не пересекаются с А. Здесь все почти идентично предыдущему случаю. Единственное - мы должны выбрать две пары связанных вершин. Обозначив через I мощность пересечения Bi и В2, мы получим следующую оценку данного события Л9(А, Bi, В2): Р (Л9(А,Ві,В2 )) * £ («(а)+1)к4е И ^М^-М^^ a=i s=0 ^'^ (й) :—S — 3к—1 •2 (п)Чг * (пользуемся леммой 3) г - 2-1 ■3—3к(2г)кк4 -1. п2 * ^(а(а) + 1)к4• 2г1—3к2к • 2 * 20г3+1—зк2кк4^2 * 20г Распишем локальный полином для даннного типа событий в точке у. Заметим, что для того, чтобы зафиксировать данную конфигурацию из ребер А, Bi и В2 для фиксированной вершины, необходимо тремя способами выбрать, какому из трех ребер принадлежит данная вершина, А(Н) способами выбрать данное ребро, пА(Н)/к способами выбрать непересе-кающееся с ним ребро, затем к способами выбрать, по какой вершине третье ребро будет пересекаться с первым или вторым, и А(Н) способами задать это ребро: <)(у) = Е Р (М^В^)) • (y)2\AUB1UB2 * (A,B1,B2)VUEAUB1UB2 1Х6к (1+к) * 3А3(Н)п • 20е6г3—3к(2г)кк4-1 * п2 * 60е6с3 (2г)к к5/2 у п <20 для достаточно малой константы с. Случай 10 Ребро А стало одноцветным цвета а в финальной раскраске, при этом изначально в нем были вершины вершины как минимум еще двух цветов. Пусть 3 — последний пропавший цвет. vi — последняя вершина цвета 3- перекрасившаяся в а. Пусть у — предпоследний пропавший цвет, V2 — последняя вершина цвета у, перекрасившаяся в а. Пусть вершины vi и V2 перекрасились в силу того, что условию перекраски удовлетворяли связанные им вершины из ребер Bi и B2, причем эти ребра не пересекаются между собой, и не пересекаются с А. Здесь мы снова вынуждены рассмотреть два варианта в зависимости от наличия дополнительных пар связанных вершин. Начнем со случая, когда таких пар нет. Пусть l — это число вершин начального цвета 3 в А, a m — это число вершин начального цвета не а и не ДА. Далее, ребро Bi изначально полиостью имеет цвет 3. ni — первая вершина Bi и она является связанной вершине vi. Аналогии но, ребро В2 изначально полностью имеет цвет 7, П2 — первая вершина В2 и она является связанной вершине Г2- Вершины начального цвета 3 в А имеют веса меньше веса vi, и они должны перекраситься в а, а все вершины начального цвета не 3 и не а в А имеют веса меньше веса V2 и они должны перекраситься в а. Обозначим описан ное событие через ДЮ> (А, Bi, B2) и оценим его вероятность: P (ДЮ) (А, Bi, B2)) С 52 k4 52 52 (k. _ 2)(k l_ - 1) • Да) • (Да) - 1) • Д(а)х i 1 m 1 = = х (^к-ит^, ((“(“) - 1)?)m(?M?)t х /‘ (Д) Jо а(а)/ M3k (1— ^iДО)dX./о (дУД) • (^Г х m—i (1 - y)k—i dyС а(а) (воспользуемся леммой 3) < EE 55а3(а)(Да) — 1)k*2r 3k(а(а) — 1)mQ 1)( 1 ) " (~) х a=i ,=i m=i х ££(1 — y)k—i(1 — x)k—i f )m i • () \ydx = \ а(а) / \а(а) (суммируем сначала по m под знаком интеграла, а потом — по l) С 55 «(«)(«(«) — 1)22г—3kk4 • a=i (5)2 х — y)k—i(1 — ^)k—i (1 + у(Да) — 1) Да) + ж a(a) k—2 dydx< < 5Ta(Q)(a(Q) — 1)22r—3kk* • a=i (^)2 х х 3 і1 ,"•"■-..,■■ 2>7g7e—<k—i)Z+(k—2>.^dyd^^ оо (пользуемся тем, что a(a) 3 2) ^ 55 a(a)(a(a) — 1)22r—3kk* • tt=i (/c-1)(y + x) “(“) dydx< < 5 a(a)(a(a) — 1)22t3kk* • (-^ • f ^(a) ) < 1152 • r3 3kk2n 2, a=1 где мы воспользовались тем, что a(a) С 4. Теперь рассмотрим ситуацию, когда в конфигурации есть дополнительная пара связанных вершин, что не позволяет рассуждать о независимости весов. Как и в предыдущих случаях, мы проигнорируем веса вершин, а только оценим вероятность того, что каждая вершина ребра А либо имела цвет а изначально, либо его не имела, но ей выпал при перекраске цвет а, каждая вершина из Ві ил и В2 получила изначально цвет этого ребра, и, наконец, есть три пары связанных вершин: щ и некоторая вершина из Ві, v2 и некоторая вершина из В2, а также еще одна пара вершин из разных ребер. Получаем следующую оценку вероятности события ДІ20(А,Ві, В2): т Р(ДІ2о)(А,Ві,В2)) ^ Е к4 • 3к2 а=1 е (к) 1=0 - ' • (о(а) + 1)2 X X (5), («(«)ТЕ,РШЬ (п)зк •2 (П)3 • (0(0))“ < (воспользуемся леммой 3) (п )3 < 300т4-3к2кк6п-3. < £ 6к6 • (о(а) + 1)2 • 2"-3к2к а=1 По условию п к к4гзк, значит, полученное выражение меньше, чем 300т3 3кк2п2. Стало быть, в итоге Р(М1о(А,В1,В2)) ^ 1500т3-3кк2п-2. Оценим локальный полином для описанного типа событий в точке у. Заметим, что для того, чтобы зафиксировать данную конфигурацию из ребер А, Ві и В2 для фиксированной вершины, необходимо тремя способами выбрать, какому из трех ребер принадлежит данная вершина.. А(Н) способами выбрать данное ребро, а налое нс более нем \Е|2< (пА(Н))2/к2 способами выбрать оставшиеся ребра: -у = Е Р (Ао((А,В1,В2))) • (£)2|AUB1UB2I ^ (A,Bi,B2):dEAUBiUB2) 1Х6к (1+к) ⩽ ^ Е 1500т3-3к к2п-2 (A,Bi,B2 ):vGAUBiUB2) ⩽ за^ГМ)' 1500е6т3-3кк2п-2 ⩽ (пользуемся тем, что А(Н) ^ стк 1к1/2) т3к-3 < 4500е6с3 т3-3кк 4500е6с3 к3/2^ 20, для достаточно малой константы с.
2.5. Завершение доказательства Завершим доказательство. Мы хотим показать, что все плохие события видов Ді — Дщ одновременно не выполнены с положительной вероятностью. Заметим, что каждое полное событие можно представить в виде дизъюнктных объединений вида С = Li С L2, где Li — это каноническое событие в смысле Лу-Секеи, т.е. Li = Д(А, В,^с), А — подмножество вершин гиперграфа Н, В С W, а ^с — это биекция между ними, a L2 = {(^у, v € В) G Q} ˜ для некоторого борелевского множества Q С R|A|. Отметим, что для любого рассмотренно- ̃︀̃︀ го в предыдущем разделе события множество А фиксировано, но меняются В,^с,а также событие L2, зависящее от весов. В работе [10] было показано, что подобные события также удовлетворяют условию отрицательной корреляции (7) при условии отсутствия конфликта между тройками. Далее, для любого события L1 П L2 поло жим dom(L1 П L2) = A U В. Ясно, что тогда события Li П L2 и L1 П L2 не конфликтуют, если dom(Li П L2) П dom(L'i П L2) = 0. Обозначим через Ф множество всех подобных плохих событий. Для применения Локальной леммы достаточно обосновать условие на локальный полином. Согласно нашему выбору DOM = VUW. Для любой г € V положим ш(у) сумме правых частей оценок всех расссмотренных плохих событий, т.е. w(y) = w((1 — у)-1) < 10у/20 < у, что и требует лемма. Если же теперь 8 € W, то тогда соответствующий полином можно оценить следующий образом: W8(у)= 52 в(c)(y)\dom^\<52 52 в(ску)^4^. Ce^:8edom(C) veV Ae^-.vedom(C),ipc(v)=8 Остается заметить, что условие /с(г) = 8 означает, что у г всегда определен цвет в начальной раскраске и вообще образ при отображении д. Значит, все оценки вероятностей Р(С) можно дополнительно поделить на п/5 (образ для г однозначно определен) и на г (нет выбора начального цвета в конфигурации). Отсюда следует, что ^8(у)< 5 max Wv(у)< |w(y) < 5у <у. г vev 3 о Теорема 2 доказана.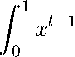
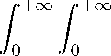
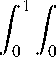
46)(у) = Е В (Ле(А,В1,В2)) • (y)2lAUB1UB2| ^
(A,Bi,B2):^gAUBiUB2
^ Е 2 • 385r-3k+3 • 1 (1 + 1} <
(A,Bi,B2)vueAUBiUB2
^ 3 • А(Н) • к • А(Н) • п • А(Н) • 770 • r3-3k • 1 (1 + 1) =
к п к
= 2310с3 ^У3 • nr-3k+31 • е6 ^ 2310 • < А
к3/2 п к3!2 20
для малой константы с.
Список литературы Справедливые раскраски гиперграфов с ограниченными степенями вершин
- Hajnal A., Szemer´edi E. Proof of a conjecture of P. Erd˝os // Combinatorial Theory and its Applications. North-Holland, London. 1970. P. 601–623.
- Erd˝os P., Lov´asz L. Problems and results on 3-chromatic hypergraphs and some related questions // Infinite and Finite Sets. — Colloquia Mathematica Societatis Janos Bolyai. 1973. V. 10. P. 609–627.
- Radhakrishnan J., Srinivasan A. Improved bounds and algorithms for hypergraph twocoloring // Random Structures and Algorithms. 2000. V. 16. P. 4–32.
- Pluh´ar A. Greedy colorings for uniform hypergraphs // Random Structures and Algorithms. 2009. V. 35. P. 216–221.
- Kostochka A.V., Kumbhat M., R¨odl V. Coloring uniform hypergraphs with small edge degrees // Fete of Combinatorics and Computer Science. — Bolyai Society Mathematical Studies. 2010. V. 20. P. 213–238.
- Shabanov D.A. On 𝑟-chromatic hypergraphs // Discrete Mathematics. 2012. V. 312. P. 441–458.
- Cherkashin D., Kozik J. A note on random greedy coloring of uniform hypergraphs // Random Structures and Algorithms. 2015. V. 47. P. 407–416.
- Akolzin I.A., Shabanov D.A. Colorings of hypergraphs with large number of colors // Discrete Mathematics. 2016. V. 339. P. 3020–3031.
- Lu L., Sz´ekely L. Using Lov´asz Local Lemma in the space of random injections // Electronic Journal of Combinatorics. 2007. V. 13. Research paper N 63.
- Shabanov D.A. Equitable two-colorings of uniform hypergraphs // European Journal of Combinatorics. 2015. V. 43. P. 185–203.
- Акользин И.А. О справедливых раскрасках простых гиперграфов // Труды МФТИ. 2017. Т. 9, № 4. С. 161–173.
- Ширгазина И.Р. Полноцветные справедливые раскраски простых однородных гиперграфов // Труды МФТИ. 2022. Т. 14, № 2. С. 169–188.
- Akhmejanova M., Shabanov D. A. Equitable colorings of hypergraphs with r colors // Journal of Mathematical Sciences volume. 2022. V. 262. P. 391–405.
- Akhmejanova M. B., Shabanov D. A. Equitable colorings of hypergraphs with few edges // Discrete Applied Mathematics. 2020. V. 276. P. 2–12.
- Alon N., Spencer J. The Probabilistic Method. 4th edition. Wiley. Hoboken, 2016.
- Kozik J. Multipass greedy coloring of simple uniform hypergraphs // Random Structures and Algorithms. 2015. V. 48. P. 125–146.


