Сравнение динамических характеристик пьезокерамических актуаторов, применяемых в вибродиагностике крупномасштабных конструкций

В процессе эксплуатации сложных инженерных сооружений возникают аварийные ситуации, предотвращение которых возможно с привлечением систем мониторинга деформационного состояния объекта. Одним из наиболее распространенных в таких системах методов является вибродиагностика. На основе анализа данных о динамическом поведении конструкции оценивается ее состояние. Обзорные работы [1 –3] демонстрируют примеры организации систем мониторинга с использованием вибродиагностики.

Возбуждение вибраций различных частотных диапазонов позволяет анализировать деформационные процессы в объекте на разных масштабных уровнях. На рисунке 1 представлена плоская рама, деформированные состояния которой сформировались в ответ на силовые импульсы различной длительности. Места приложения и направления импульсов показаны стрелками. Силовой импульс, провоцирующий собственные колебания низкой частоты, приводит к довольно равномерному деформированию всей конструкции (Рис. 1а ). Импульс в среднем диапазоне частот вызывает деформирование на уровне структурных элементов и не искажает форму конструкции в целом (Рис. 1б ). Высокочастотный импульс порождает локальный вибрационный процесс в окрестности точки его приложения (Рис. 1в ).

Известные методы вибродиагностики используют разные частотные диапазоны воздействия на инспектируемую конструкцию с целью получения отклика на интересующем масштабном уровне.

К первой группе относятся методы, которые базируются на возбуждении низкочастотных колебаний. Они применяются при анализе собственных форм и частот колебаний сложных пространственных конструкций [4 –8] . Источниками низкочастотных вибраций могут служить случайные или регулярные воздействия природного или техногенного характера, например, порывы ветра, проезд транспорта, микросейсмические колебания земной поверхности. Такие методы относятся к пассивной вибродиагностике. Они технически хорошо реализуемы, но требуют обработки непрерывного потока данных с целью выделения интервалов времени, в течение которых колебания, характеризующие собственные частоты, измеряются достоверно. Для возбуждения низкочастотных

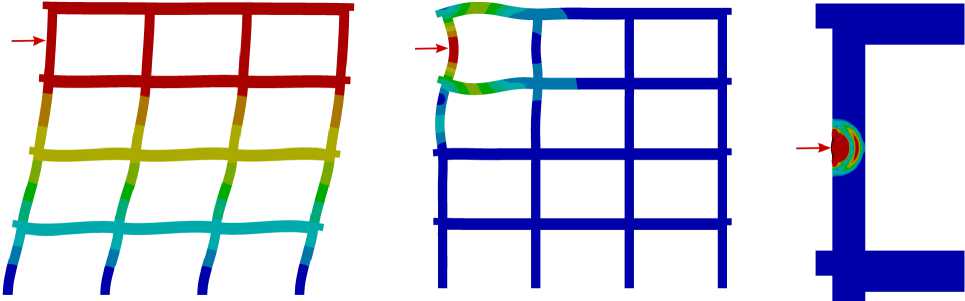
Рис. 1. Деформационный отклик конструкции на силовые импульсы трех частотных диапазонов: низшего ( а ), среднего ( б ), высокого ( в )

колебаний может использоваться и активная вибродиагностика, при которой колебания инициируются специальными вибраторами или устройствами, производящими ударные импульсы. Как известно, с ростом собственных частот увеличивается плотность их спектра и, как следствие, затрудняется их идентификация. Кроме этого, появление в объекте дефектов оказывает на собственные частоты неравномерное влияние: одни из них изменяются в большей степени, другие — в меньшей. Возможны случаи, когда частоты совпадают или меняются местами. Достигнуть однозначности идентификации удается за счет контроля формы колебаний, но в этом случае требуется увеличение числа датчиков, а также синхронизация сбора данных. У методов первой группы есть важное достоинство — возможность контроля низших собственных частот даже одним датчиком, если его расположение выбрано удачно. Однако при этом оценивается состояние всей конструкции, в том числе условия на границе, а установить причину изменения частоты и определить места появления вероятных дефектов можно только или при анализе нескольких частот, или при совместном рассмотрении форм и частот колебаний. Следует отметить, что чем ниже частота колебаний, тем она менее чувствительна к возникшим локальным дефектам.

Вторая группа вибродиагностических методов использует вибрации среднего частотного диапазона. При этом возбуждаются колебания (изгибные и крутильные) отдельных структурных элементов, таких как колонны, плиты или составные элементы ферменных конструкций. Вибрации на этих частотах характеризуются небольшим затуханием при распространении в объекте и позволяют более детально анализировать повреждения. Вместе с тем появление колебаний связано с применением актуаторов, поскольку естественных источников вибраций этого диапазона частот в конструкции, как правило, нет. Диагностическая процедура может включать гармоническое [9 –11] или импульсное [12 –14] возбуждение. При гармоническом воздействии строятся амплитудно-частотные характеристики (АЧХ) в точках регистрации отклика. Совокупность АЧХ, полученных от актуаторов, находящихся в разных точках конструкции, характеризует ее состояние в целом. При гармоническом воздействии на АЧХ влияют все элементы конструкции и граничные условия. Чувствительность к наличию дефекта увеличивается по мере приближения к нему точки регистрации, но удаленные дефекты также оказывают влияние на АЧХ. При рассмотрении переходных (волновых) процессов, вызванных импульсным возбуждением, исследуется перемещение фронта деформационной волны. Из анализа движения фронта на временном интервале соответствующего размера можно получить волновую картину, лишенную искажений за счет отражения волны на границах элементов конструкции. Чем меньше интервал времени наблюдения, тем более локализованная диагностика может быть проведена. Так можно исследовать распространение деформационной волны по разным траекториям и тем самым контролировать состояние проблемных зон. Методы второй группы являются универсальными, но требуют сложных алгоритмов обработки данных.

Методы третьей группы анализируют изменение деформационного состояния конструкции в ответ на возбуждение колебаний высокочастотного диапазона, к которым относятся волны Лэмба, поверхностные волны Релея, объемные S- и P-волны [15, 16] . При этом удается получить самую высокую детализацию дефектов. Однако высокочастотные колебания быстро затухают при распространении по конструкции. Поэтому их использование для организации непрерывного контроля всех элементов крупномасштабного объекта нецелесообразно, так как для этого требуется плотная сеть актуаторов и датчиков. Как правило, с помощью таких волн организуется контроль наиболее ответственных элементов или проводится детальная диагностика зон с дефектами.

Таким образом, при проведении вибродиагностики крупномасштабных конструкций частотный диапазон воздействия нужно соотносить с масштабами деформационных процессов, которые требуется оценить. Низкочастотные колебания обладают низкой чувствительностью к образованию локальных дефектов. С ростом частоты, с одной стороны, чувствительность к появлению дефектов увеличивается и повышается достоверность их локализации, но, с другой стороны, упругие волны, по мере их распространения в конструкции, затухают быстрее. Поэтому для организации вибрационного мониторинга наиболее перспективным является возбуждение колебаний среднего частотного диапазона. Они обеспечивают достаточную локализацию дефектов при приемлемом уровне затухания диагностических сигналов и предполагают использование актуаторов, поскольку в предмете исследования естественные источники вибраций с необходимыми частотными характеристиками, как правило, отсутствуют.

Актуаторы бывают маятниковые, электромагнитные, пьезокерамические. В сравнении с другими, пьезокерамические актуаторы обладают следующими достоинствами [10, 17] : в их конструкции обычно нет трущихся и ударно взаимодействующих частей, что обеспечивает высокую надежность и точность передачи сигналов; они позволяют реализовать импульсные и гармонические возбуждения, основная частота которых может изменяться в процессе выполнения диагностических процедур; они способны быть источниками высокочастотных (ультразвуковых) сигналов.

На сегодняшний день наибольшее распространение получили актуаторы из пьезокерамики, внедряемые в бетон [9, 11] . Также известно размещение пьезокерамических актуаторов на поверхности конструкции [18] . Еще один вид актуатора на основе пьезокерамики предложен авторами данной статьи (см. [19] ). В конструкцию актуатора входит присоединенная масса, за счет которой удается значительно интенсифицировать его воздействие. Повышение амплитуды диагностических сигналов является важной задачей, поскольку позволяет снизить общее количество актуаторов и сенсоров при диагностике крупномасштабных конструкций путем увеличения расстояния между ними.

Настоящее исследование посвящено сопоставлению динамических характеристик пьезокерамических актуаторов разных видов. Представлены результаты численного эксперимента, моделирующего процесс распространения волн в бетонных конструкциях, возбуждаемых пьезокерамическим актуатором. Анализируется интенсивность сигнала по мере удаления от актуатора. В качестве источников колебаний рассматриваются три вида актуаторов. Первый и второй из них состоят из одной пьезокерамической пластины, при этом в первом случае пластина размещается на поверхности исследуемого объекта (далее расчетный вариант 1), а во втором — внедрена в бетон (вариант 2). Действие пьезокерамического актуатора в третьем случае (вариант 3) усиливается за счет дополнительной массы. Описание и технические возможности актуатора с дополнительной массой можно найти в [19] . Цель настоящей работы заключается в сопоставлении возможностей различных актуаторов при их использовании в вибродиагностике крупномасштабных бетонных конструкций.

• 2.    Расчетные схемы

• 3.    Математическая постановка

Во всех вычислительных экспериментах пьезокерамический элемент представляет собой круглую пластину толщиной 6 мм и диаметром 30 мм. Дополнительная масса в усиленном актуаторе составляет 1.3 кг. Волновой процесс, вызванный воздействием такого актуатора, демонстрируется на примере двух конструкций — бетонном диске диаметром D = 4 м и толщиной T = 0.1 м (Рис. 2) и модельном железобетонном 4-этажном здании (Рис. 3) . Габаритные размеры здания: высота H = 6 м, ширина W = 4 м, длина L = 6 м, высота колонн 1.5 м, шаг распределения колонн 2 м. Актуатор располагается в центре О бетонного диска (Рис. 2г ) и в точке О на одной из внешних колонн здания (Рис. 3г ).

Рассмотрено шесть расчетных схем взаимодействия актуаторов с тестируемой конструкцией (3 варианта актуаторов на двух модельных объектах). Описание расчетных схем и последующая математическая постановка выполняются в правой прямоугольной системе координат Ox 1 x 2 x 3 . На рисунках 2 и 3 элементы расчетных схем пронумерованы следующим образом: 1 — диагностируемый объект, 2 — пьезокерамическая пластина, 3 — адаптер, 4 — присоединенная масса. Контактирующие элементы считаются жестко соединенными между собой. Для наглядности отображения положения актуатора на конструкции на рисунках 2а , 2в , 3а , 3в ) не показана часть области {x 1 > 0, x ₂ > 0}, а на рисунках 2б , 3б ) — часть области {x ₂ > 0, x ₃ > 0}.

Исследуются динамические деформационные процессы, возникающие при взаимодействии актуатора с диагностируемой конструкцией. Инициация возбуждения реализуется за счет подачи на пьезокерамический элемент одиночного импульса напряжения. Элементы из металла и бетона считаются однородными и изотропными. Деформирование металла и бетона описывается соотношениями линейной теории упругости [20] . Физические уравнения для бетона включают слагаемые, учитывающие диссипацию энергии за счет сил внутреннего трения [21] . Пьезокерамика является поликристаллическим материалом, в каждом кристалле которого находятся

( а )                             ( б )                             ( в )                                                                ( г )

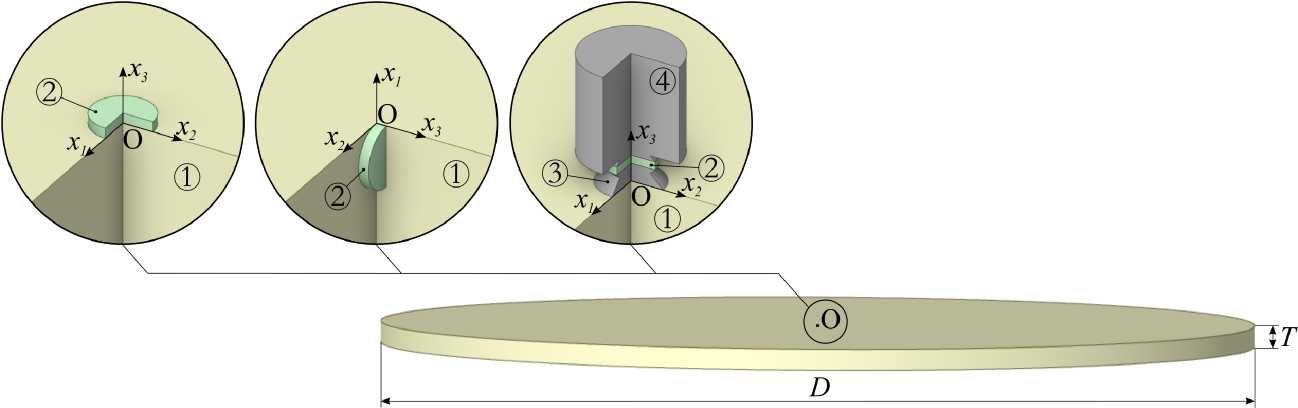
Рис. 2. Схемы установки актуатора на плите: пьезокерамическая пластина на поверхности – вариант 1 ( а ); пластина, внедренная в бетон, – вариант 2 ( б ); актуатор с присоединенной массой на поверхности – вариант 3 ( в ); положение актуатора на тестируемой плите ( г )

( а )                             ( б )                             ( в )                                                                ( г )

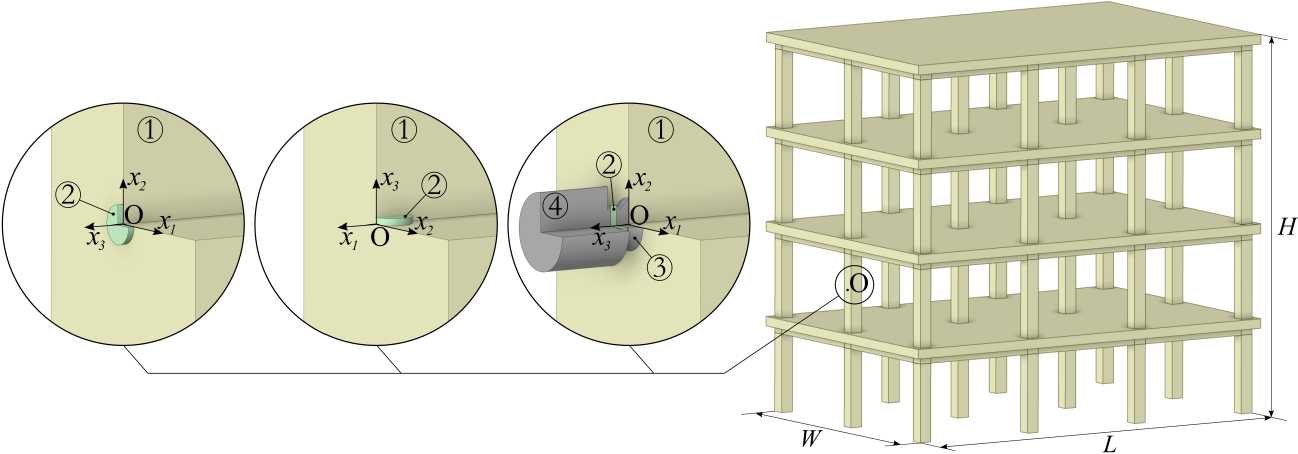
Рис. 3. Схемы установки актуатора на модельном здании: пьезокерамическая пластина на поверхности – вариант 1 ( а ); пластина, внедренная в бетон – вариант 2 ( б ); актуатор с присоединенной массой на поверхности – вариант 3 ( в ); положение актуатора на колонне модельного здания ( г )

элементарные диполи, обусловленные несимметрией строения кристаллов [22] . Такое строение позволяет пьезокерамическому элементу изменять свои размеры в электрическом поле или генерировать электрическое поле при изменении размеров. Этот материал характеризуется вектором поляризации и анизотропными электроупругими характеристиками. Его деформирование описывается в рамках связанной электромеханической постановки [22] . Во всех рассматриваемых расчетных схемах вектор поляризации пьезокерамики направлен вдоль оси x ₃ .

Математическая постановка задачи включает:

• – уравнения движения

  дЛ = _p ( k ) dUUl. dxj          dt²

  
  

  x e V ^{( k )} ,    i,j G{1,2,3},    k e{1,2,3,4},

  
  
  
  

где верхний индекс k определяет принадлежность к соответствующему элементу расчетной схемы (см. Рис. 2, 3), a ij^{( k )} , U i^{( k )} — компоненты тензора напряжений и вектора перемещений в декартовой системе координат, p ^(k) и V ^(k) — плотность и объем соответствующего тела, t — время, x = (x i ,x ₂ ,x ₃ ) — радиус-вектор точки;

– уравнения электростатики dDi(k)=0

∂xi      , x € V(k),  i €{1,2,3},  k = 2,

E.™ = -     ,

∂xi где D(k), E-Sk — компоненты векторов электрической индукции и напряженности электрического поля в декартовой системе координат, ф(k) — электрический потенциал;

– геометрические соотношения

Eij ™ =2 С ⁺ j \ x € V ( k ) , i,j €{1,2,3},   k €{1,2,3,4},

2 у Cd ^X j        ^d ^X i   у где Eij(k) — компоненты тензора деформации;

- физические соотношения для пьезокерамики, поляризованной вдоль оси х ₃ (верхний индекс k, определяющий принадлежность к пьезоэлементу, в них опущен)

^ 11 = C 11 E 11 + C 12 E 12 + C 13 E 33 — е зх Е з ,

02 2 = C 12 E 11 + C 11 E 22 +C 13 E 33 — е з1 Е з ,

0 33 = C 13 E 11 + C 13 E 22 + C 33 S 33 — e 33 E 3 ,

• ^o 23 = ^c 44 ^E 23 ^{— e} 15 E 2 ,

0 13 = C 44 E 13 — e 15 E 1 ,                x € V ⁽²⁾ ,                             (4)

0 12 = ⁽¹/²)^{( c} 11 ^— c 12 ) ^E 12 ,

D 1 = ^a 11 E 1 + ^e 15 ^E 12 ,

D 2 = a 11 E 2 +6 15 3 23 ,

D 3 = ^a 33 E 3 ^{+ e} 31 ^E 11 ^{+ e} 31 ^E 22 ^{+ e} 33 ^E 33 .

Здесь cn, c ₁₂ , c ₁₃ , c ₃₃ , c ₄₄ — модули упругости; e ₃₁ , e ₁₅ , e ₃₃ — пьезомодули; an, a ₃₃ — коэффициенты диэлектрической проницаемости;

– физические соотношения для металла

O ij ^(k) = K ^{( k )} e ^{( k )} 5 ij + 2G ^(k) dij ^{( k )} , x € V ^(k) , k €{3,4};                             (5)

– физические соотношения для бетона

• oij ^(k) = K ^(k) 0 ^(k) 5 _ij + 2G ^(k) d _ij ^(k) +в ( к ^{( k )} Q ^{( k )} ^ _ijj +2 G ^{( k}' ⁾ d _ij ^(k) ) , x € V ⁽¹⁾ , k = 1.             (6)

В (5) и (6) приняты обозначения: K ^(k) , G ^(k) — объемный и сдвиговой модули соответствующих материалов; β — параметр, определяющий диссипативные свойства бетона [21] ; δij — символ Кронекера; d ij ^(k) = E ij ^(k) — Ok^Sij /3 — компоненты девиатора тензора деформации; 0 ^(k = E ₁₁ ^(k) + e ₂₂ ^(k) + E ₃₃^(k) — объемная деформация; точка над символом означает производную по времени;

– граничные условия для электрических переменных

Ф ^(k) = 0, x € S ^(k) ,

Ф ^(k) = ф*, x € S $ ^k) ,             k = 2,                                (7)

D ^(k) n ^(k) =0, x € sD ^k) , i €{1,2,3},

• ( k )        ( k )

где Sq и S+ — электродированные поверхности пьезокерамического элемента с нулевым и заданным электрическим потенциалом ф*, Sk — неэлектродированные поверхности пьезокеармики, nj(k) — компоненты единичного вектора нормали к поверхности k-го тела. Пьезокерамический элемент имеет форму цилиндра, его ось вращения направлена вдоль координатной оси x3, S(k) — поверхность его основания (x3 = 0), а Sk) — поверхность верхнего торца. В результате задания положительного потенциала на S+k) формируются напряжения, растягивающие пьезокерамическую пластинку вдоль оси хз;

– граничные условия для механических переменных

( k ) ( k )                     ( k )

j nj =Л         ^, ij e{1,2,3},   ke{1,2,3,4},

Ui~ ' =0, xeSu , где Sf(k), Su (k) — свободные и жестко закрепленные поверхности k-го тела;

– условия для механических переменных на контактных поверхностях

ТТ. (k1)=TT.(k2)

Ui (_М Uk i ) J    ( k 2 )   ( k 2 )      ij e{1,2,3}, x e S ^{(k 1} , ^{k 2 )} ,   (k ₃ ,k ₂ ) e{(1,3),(2,3),(2,4)} ,

^ij   'nj       ^ij   njj    , где S(k1’k2) — контактирующие поверхности тел с индексами k1 и k2. Условия контакта для электрических переменных не представлены, поскольку при расчетах рассматривается только одно электроупругое тело.

Электрические и механические характеристики пьезокерамики ЦТС-19, использованные в вычислительных экспериментах, приведены в таблице 1. Параметры бетона и металла содержит таблица 2. В качестве допустимой напряженности электрического поля, прикладываемого к пьезокерамике, принято значение 2'10 ⁶ В/м. Предельные сжимающие и растягивающие напряжения для пьезокерамики, соответственно, равны –290 МПа и +15 МПа.

Таблица 1. Электромеханические параметры пьезокерамики ЦТС-19

A 11 , ГПа	A 12 , ГПа	A 13 , ГПа	A 33 , ГПа	A 44 , ГПа	α 11 /ε 0	α 33 /ε 0	ε 0 , Ф/м	e 31 , K/м 2	e 33 , K/м 2	e 15 , K/м 2	ρ (2) , кг/м 3
109	61	57	93	24	840	820	8.85·10 - 12	-4.9	14.9	10.9	7740

Таблица 2. Механические параметры бетона и металла

K (3) , K (4) ,	G (3) , G (4) ,	ρ (3) , ρ (4) ,	K (1) ,	G (1) ,	ρ (1) ,	β ,
ГПа	ГПа	кг/м 3	ГПа	ГПа	кг/м 3	с
166.6	76.9	7850	26.8	14.5	2400	3.464·10 - 7

Численная реализация задачи в представленной математической постановке осуществлялась с помощью конечно-элементного комплекса ANSYS. Рациональная степень дискретизации конечных элементов и выбор необходимого шага по времени устанавливались в ходе вычислительных экспериментов.

• 4.    Результаты моделирования

На основе математической постановки (1) – (8) методом конечных элементов решена задача динамического деформирования конструкции под действием пьезокерамического актуатора. Форма электрического сигнала Ф * (t), подаваемого на пьезокерамический актуатор, показана на рисунке 4а . Это одиночный импульс длительностью 0.2 мс с амплитудой 10 кВ, который приводит к удлинению актуатора вдоль оси х ₃ и укорачиванию в поперечном направлении. Вследствие этого на конструкцию оказывается силовое воздействие. При размещения пьезокерамического актуатора на поверхности (вариант 1, Рис. 4б ) доминирующим возбуждением со стороны актуатора является осесимметричное сжатие поверхности бетона в зоне контакта. При варианте 2 (Рис. 4в ) преобладает усилие, вызванное растяжением пластины в направлении оси х ₃ . При посредстве усиленного актуатора (вариант 3, Рис. 4г ) реализуется сжимающее усилие по нормали к поверхности бетонной плиты.

Волновые процессы в бетонной плите, вызванные силовым воздействием актуаторов, иллюстрирует рисунок 5. На нем показано распределение компоненты перемещений, направленной по нормали к плите, в момент t = 0.64 мс от начала подачи электрического сигнала на пьезокерамику. Рисунок отвечает трем вариантам силового воздействия актуатора, показанным на рисунке 4. Для каждого из них результаты представлены в сечении плиты вертикальной плоскостью, проходящей через ее центр (см. верхний ряд), и на верхней поверхности плиты (см. нижний ряд). Для наглядности отображения деформированной плиты значения перемещений в верхнем ряду увеличены в 8-10 ⁶ , 4 • 10 ⁶ и 4-10 5 раз соответственно.

Согласно рисунку 5, при первом (5а ) и третьем (5в ) вариантах размещения актуаторы дают симметричный фронт волны. При внедрении в бетон (5б ) формируется несимметричная деформационная волна с преимущественным

( г )

( a )

( б )

( б )

Рис. 4. Форма электрического сигнала ( а ) и схемы силового воздействия актуаторов: вариант 1 ( б ), вариант 2 ( в ), вариант 3 ( г )

( а )                                                   ( б )                                                   ( в )

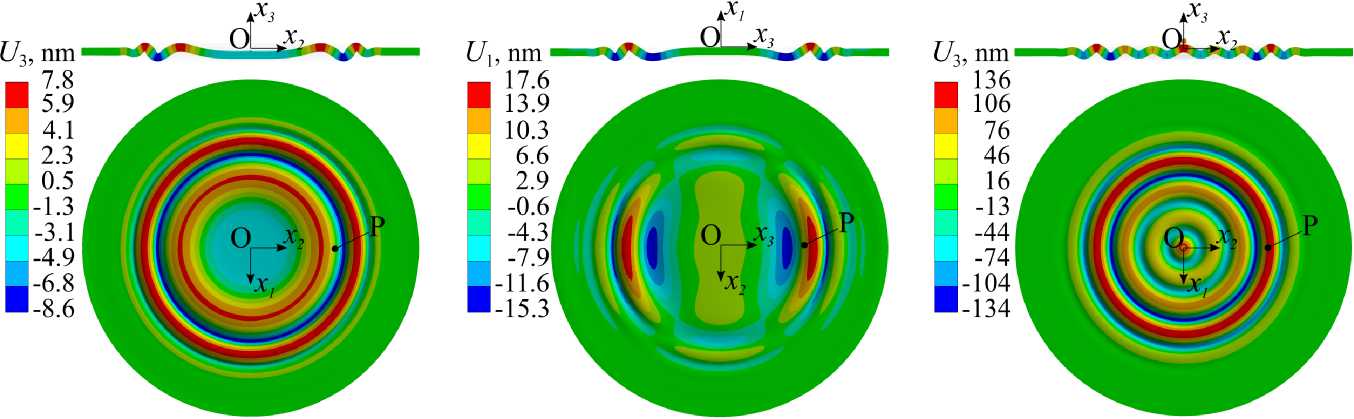
Рис. 5. Изополя компоненты перемещения, направленной по нормали к поверхности плиты, для трех видов актуатора: вариант 1 ( а ), вариант 2 ( б ), вариант 3 ( в )

распространением в направлении оси x 3 . Амплитуда генерируемой при этом деформационной волны существенно отличается. Так, при расположении на поверхности плиты (Рис. 5а ), актуатор формирует волну с максимальным значением амплитуды, равным 7.8 нм. При заглублении в бетонное тело (Рис. 5б ) возбуждается волна с амплитудой 17.6 нм, что превосходит амплитуду волны при поверхностном креплении пьезоэлемента в 2.2 раза. Использование актуатора, усиленного присоединенной массой (Рис. 5в ), позволяет получить перемещения на фронте волны с амплитудой 136 нм, что в 17 раз больше значения, соответствующего варианту 1.

На рисунке 6 для сопоставления представлены ускорения на поверхности бетонной плиты, возникающие при различных вариантах расположения пьезокерамического элемента. Приведенные виброграммы ускорения, направленного по нормали к поверхности плиты, соответствуют точке P на рисунке 5, находящейся на расстоянии 1 м от центра актуатора. Видно, что виброграммы отличаются как по форме, так и по амплитуде. Наименьшая амплитуда ускорений на фронте волны имеет место при креплении пьезокерамического элемента на поверхности плиты (вариант 1) и составляет 10 м/с ² . При вариантах 2 и 3 это значение оказывается больше в 2 и в 12 раз соответственно. Здесь необходимо заметить, что ускорения, реализующиеся во всех рассмотренных случаях, надежно регистрируются современными акселерометрами.

( а )                                                   ( б )                                                   ( в )

Время, мс                                Время, мс                                Время, мс

Рис. 6. Виброграммы ускорений для трех вариантов расположения актуатора: вариант 1 ( а ), вариант 2 ( б ), вариант 3 ( в )

Аналогичная серия вычислительных экспериментов проведена для исследования деформационного процесса, развивающегося в модельном 4-этажном железобетонном здании. Рисунок 7 демонстрирует распространение волны перемещений, инициированной актуатором с присоединенной массой. Актуатор находится на внешней колонне первого этажа (Рис. 3г). Изополя перемещений соответствуют трем моментам времени от момента подачи электрического импульса на актуатор. Для наглядности деформированная конструкция изображена с увеличением перемещений в 2· 105 раз. На рисунках значения перемещений, превышающие 0.9· 1012 м, показаны белым цветом, что позволяет отслеживать положение фронта волны в разные моменты времени. Видно, что после генерации актуатором силового импульса волна распространяется по колонне в противоположные стороны от места возбуждения. Когда волна достигает стыка колонны с плитой, происходит ее разделение: одна часть проходит дальше по колонне, другая часть уходит в плиту, третья часть отражается от стыка. В плите волна распространяется аналогичным образом: при столкновении с колонной она делится на части: одна часть огибает колонну, при этом фронт волны искажается; вторая часть уходит в примыкающие сегменты колонн; третья часть отражается. Таким образом, фронт волны по мере распространения в конструкции эволюционирует.

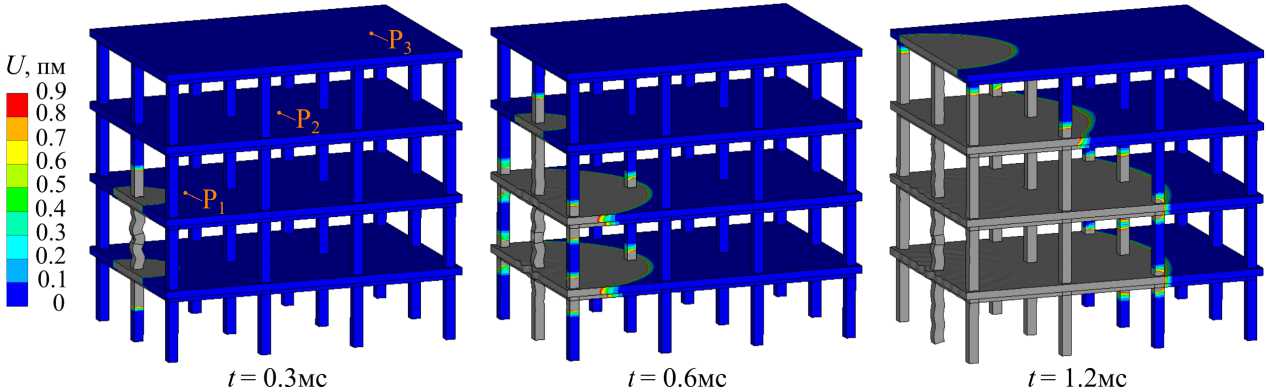
Рис. 7. Эволюция фронта деформационной волны: значения амплитуды вектора перемещения больше 0.9·10 ^{- 12} м показаны белым цветом

Представляла интерес оценка изменения интенсивности деформирования железобетонной конструкции по мере удаления от места приложения силового импульса. На рисунке 7 показаны 3 точки на каркасе модельного здания, для которых рассчитаны виброграммы ускорений. Эти точки располагаются на разных этажах и разном удалении от колонны, на которой установлен актуатор. Виброграммы компоненты ускорения, направленной по нормали к поверхности колонны, соответствующие трем вариантам расположения актуатора, приведены на рисунке 8, при этом столбцы на рисунке соответствуют виду актуатора, а строки — определенной точке регистрации.

Все виброграммы, приведенные на рисунке 8, свидетельствуют, что амплитуда ускорений быстро уменьшается при удалении от места возбуждения. Сопоставление виброграмм, полученных для модели здания и бетонной плиты, показывает, что в конструкции сложной пространственной конфигурации происходит более интенсивное затухание волнового процесса. Так, если в плите на расстоянии 1 м от точки импульсного воздействия максимальное ускорение составляет 10 м/с ² , то в многоярусном здании в точке P 1 (на расстоянии 1.7 м от актуатора) оно равно 1.5 м/с ² .

Интенсивность вибрационного процесса, инициируемого актуаторами разного вида, существенно отличается. Как отмечено ранее при рассмотрении бетонной плиты, наибольшие амплитуды ускорений отмечаются при использовании актуатора с присоединенной массой (Рис. 8в ), а наименьшие — при возбуждении вибраций с помощью пьезокерамической пластины на поверхности колонны (Рис. 8а ). В точке P ₁ , расположенной на расстоянии 1.7 м от места воздействия, амплитуды ускорения составляют 1.5, 6 и 20 м/с ² для вариантов актуатора 1, 2 и 3 соответственно.

Применение актуаторов в активной вибродиагностике сложных пространственных конструкций ставит вопрос о «зоне видимости» актуатора, то есть о возможности регистрации создаваемых им сигналов на определенном удалении от него.

Проведем оценку уровня сигнала, который измерен наиболее распространенным типом акселерометров. Среднеквадратичное значение собственных шумов акселерометра ВС110 фирмы ZETLAB не превышает 0.005 м/с ² . Если считать, что регистрируемое значение сигнала должно превосходить уровень шума не менее чем в 10 раз, то его пороговое значение составляет 0.05 м/с ² . Сопоставление этого значения с виброграммами, приведенными на рисунке 8, показывает, что максимальные значения ускорений превосходят пороговый уровень во всех точках замеров при всех вариантах расположения актуатора. Следовательно, колебания конструкции будут зафиксированы датчиками данного типа, установленными во всех указанных точках. Однако при вибродиагностике важно контролировать именно распространение фронта деформационной волны. Это значит, что нужно оценивать уровень сигнала на начальном участке виброграммы. Для 1-го варианта актуатора (Рис. 8а ) вибрационный сигнал, достигший точек P ₂ иP ₃ , имеет на фронте волны амплитуду 0.031 и 0.009 м/с ²

( а )

( б )

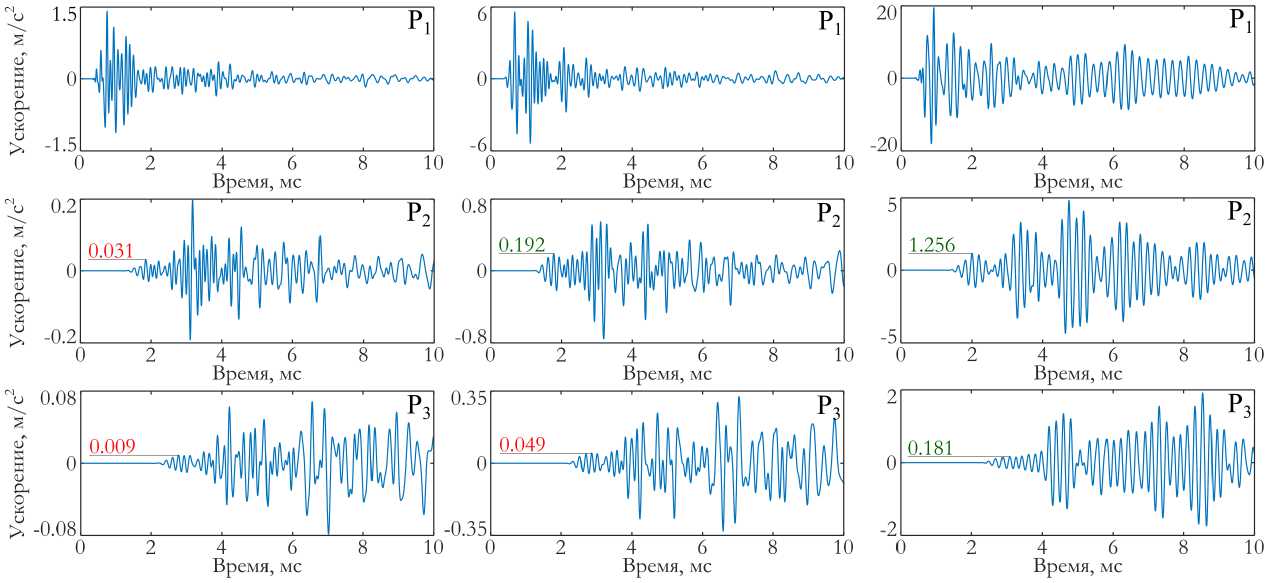
Рис. 8. Виброграммы ускорения в различных точках модельного здания для трех видов актуатора: вариант 1 ( а ), вариант 2 ( б ), вариант 3 ( в )

( в )

соответственно. Эти значения ниже установленной пороговой величины, то есть момент прихода деформационной волны в данные точки конструкции не может быть достоверно зарегистрирован акселерометром этого типа. Актуатор, погруженный в бетон (Рис. 8б ), генерирует деформационную волну, появление которой регистрируется датчиками, расположенными в точках P 1 иP 2 , но не улавливается в точке P 3 . Актуатор, усиленный присоединенной массой, возбуждает в модельной конструкции волновой процесс, надежно регистрируемый во всех трех точках.

• 5.    Заключение

Активная вибродиагностика с применением пьезокерамических актуаторов является эффективным методом оценки механического состояния конструкций. В работе рассмотрено три вида пьезокерамических актуаторов, предназначенных для вибродиагностики железобетонных конструкций. В них в качестве источника вибраций используется пьезокерамическая пластина, размещенная на поверхности бетона, заглубленная в бетон и усиленная дополнительной массой. С помощью вычислительных экспериментов продемонстрировано распространение деформационной волны, возбуждаемой этими видами актуаторов, в бетонной плите и в модельном пространственном железобетонном сооружении вида 4-этажного здания.

На основе полученных результатов сделаны следующие выводы:

– уровень силового воздействия у актуаторов разного вида существенно отличается. Пьезокерамическая пластина, расположенная на поверхности бетона, вызывает самый низкий деформационный отклик инспектируемого объекта. Амплитуда деформационной волны в этом случае оказывается ниже в 1.9 раз, чем при актуаторе, заглубленном в бетон, и в 12 раз ниже по сравнению с усиленным актуатором;

– пьезокерамическая пластина, заглубленная в бетон, возбуждает несимметричную деформационную волну, имеющую наибольшую амплитуду вдоль вектора поляризации пьезокерамики. Это обстоятельство важно учитывать при выполнении вибродиагностики;

– в конструкциях сложной пространственной конфигурации процесс распространения деформационной волны происходит нетривиальным образом: он сопровождается перераспределением и отражением волны на составляющих ее элементах, что способствует затуханию колебаний. Актуаторы, не усиленные дополнительно, могут оказаться неспособными возбудить сигнал, который может быть зарегистрирован на достаточном удалении от точки воздействия. В этом случае наилучшим решением представляется применение актуатора с присоединенной массой, порождающего деформационный отклик значительно большей интенсивности. Численный эксперимент показал, что вибрационная волна, возбуждаемая таким актуатором, успешно распространяется на значительное (более 9 м) расстояние от его местонахождения.

Таким образом, для выполнения активной вибродиагностики крупномасштабных бетонных конструкций наиболее перспективным является пьезокерамический актуатор с присоединенной массой. Он обеспечивает существенное повышение амплитуды диагностических сигналов по сравнению с актуаторами в виде пьезокерамической пластины. Использование усиленных актуаторов позволяет снизить общее количество актуаторов и сенсоров системы мониторинга за счет увеличения расстояния между ними.

Работа выполнена в рамках государственного задания, регистрационный номер темы 124020700047-3.