Сравнение классического и модифицированного методов расчета фрактальной размерности временных рядов с помощью показателя Херста

Современные средства программирования позволяют создавать аналитические платформы, которые предназначены для анализа и прогнозирования поведения сложных систем функционирование которых не подчиняется гипотезе о нормальности распределения исследуемых величин, а описывающие их временные ряды обладают свойством персистентности.

Целью настоящего исследования является разработка программного комплекса, предназначенного для решения задачи определения дробных размерностей временных рядов на основе их R/S анализа и расчета показателя Херста.

Постановка задачи r = r (t)

Пусть t-Т     - временной ряд. Тре буется определить фрактальную размерность ряда, размерность Мандельброта и корреляционное соотношение методом R/S анализа.

Метод решения

• 1.    Классический метод

Введем формальное описание классического метода, основы которого сформулированы в [1, 2].

• a.    Формирование окон (временных ин-

• _ о                те[т0,T/21      о

тервалов) шириной       0       от на-

„                  ^то >¹ „ „ _ Ат > 1

чального значения ⁰ с шагом ^ ^{т — 1}:

т = т₀ , Т/ 2, Ат

• b.    Расчет среднего значения измеренной

r (1)

величины ^x ' для всех окон ширины т , укладывающихся в T:

• 1    „ . .

*'     ^ r ( t )

т t = 1

• c.    Определение накопленной суммы отклонений от среднего для всех окон:

t

рт(t )=Е(r (i)-rO ( t=1,т) i=1

.

• d.    Вычисление размаха для всех окон:

R ( т ) = max P ( t ) - min P ( t )

^{V 7}    t е [ 1, т ] ^{Л 7}     t е [ 1, т ] ^{тХ 7}

• e.    Расчет стандартного отклонения:

• 2.    Модифицированный метод

S (т)=, 77 S( r(t)-гт)2

V ^т - ¹ 1 = 1

T

^Т€ f Для всех окон ширины ^    _

R (т)

рассчитывается среднее значение

Методологические и прикладные аспекты модифицированного (упрощенного по сравнению с классическим) изложены в [3, 4]. Рассмотрим основные этапы этого метода.

• a.    Формирование окна (временного ин-

• те[т0, T ]

тервала) шириной      0 от начально- т > 1

го значения ⁰ с шагом ^{Ат — 1}:

т = т₀ , T , Ат

.

• b.    Расчет среднего значения измеренной

r (t)

величины     в текущем окне:

т

r    Z r ( t )

т t = 1

• c.    Накопленная сумма отклонений от среднего:

t

рт( t )=£( r (i)-rr) (t=1,т)

i = 1

• d.    Размах на текущей ширине окна:

R ( т ) = max P ( t ) - min P ( t )

t е [ 1, т ] ^т            t е [ 1, т ] ^т

• e.    Расчет стандартного отклонения:

• ^{5 ( т )}=, т4 х⁽ r ⁽ t ^{) -} r - ^{) 2}

V ^т - ¹ 1 = 1

т G [ т₀ , T ]

• f.    Для каждого окна ширины     ⁰

рассчитывается (единственное) значение

1 (т)

S

.

c ^т H = ^{1 ( т )}

«Экспонента Херста» S , где с – второстепенный параметр позволяет определить искомый коэффициент H.

Характеристики временных рядов в зависимости от величины их фрактальной размерности достаточно подробно описаны, например в [1, 3]

Программная реализация и практическая апробация

На рисунке 1 представлено основное окно программы, в котором представлены исходные данные и начальные параметры показателей, используемых в расчетах.

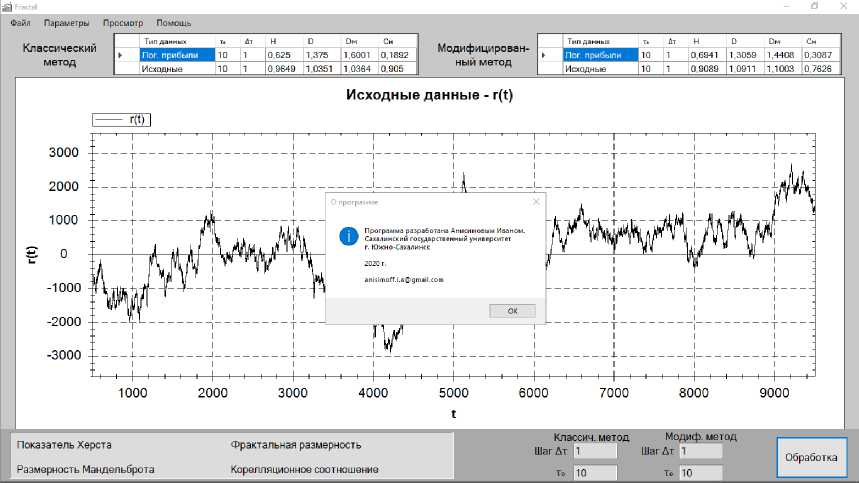
Рис. 1. Основное окно программы

Программа осуществляет расчет фрактальной размерности как для абсолютных значений исходных данных по врменному ряду, так и для так называемых логарифмичесих прибылей, что позволяет исключить взаимное влияние соседних данных. Пример графика логарифмических прибылей представлен на рисунке 2.

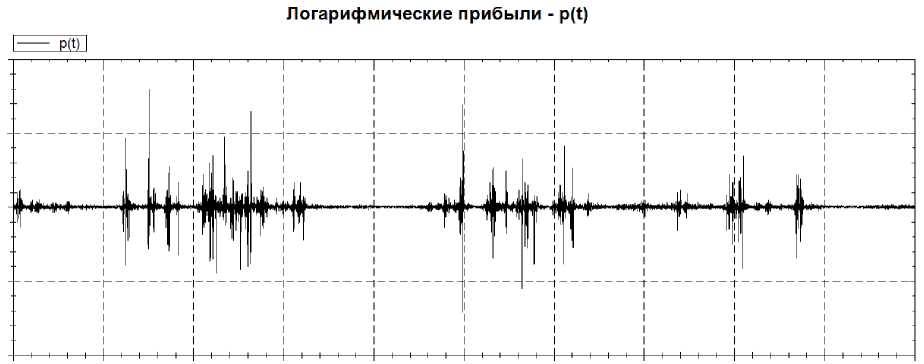
Рис. 2. Логарифмические прибыли

Программа обеспечивает возможность осуществления R/S анализа как классическим методом, так и модифицированным.

На рисунке 3 представлена экспонента Херста в двойной логарифмической шкале.

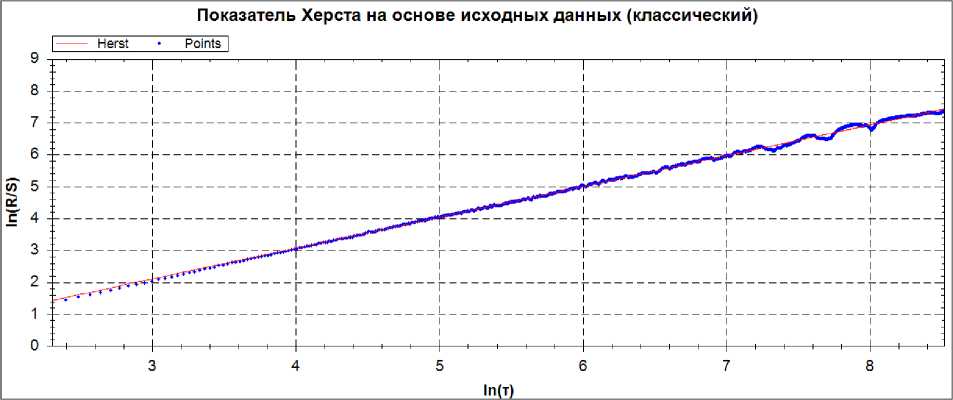
Рис. 3. Пример расчет показателя Херста. Классический метод

На рисунке 4 приведен пример расчета показателя Херста модифицированным методом.

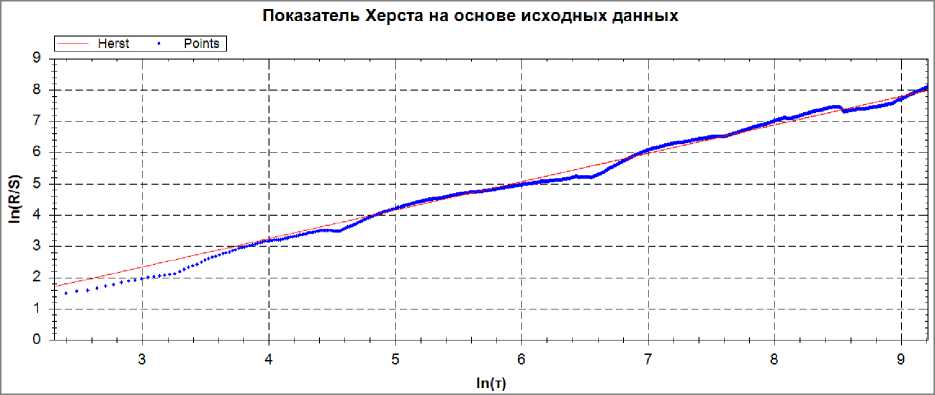
Рис. 4. Пример расчета показателя Херста. Модифицированный метод

На рисунке 5 приведен результат определения показателя Херста при использовании логарифмических прибылей.

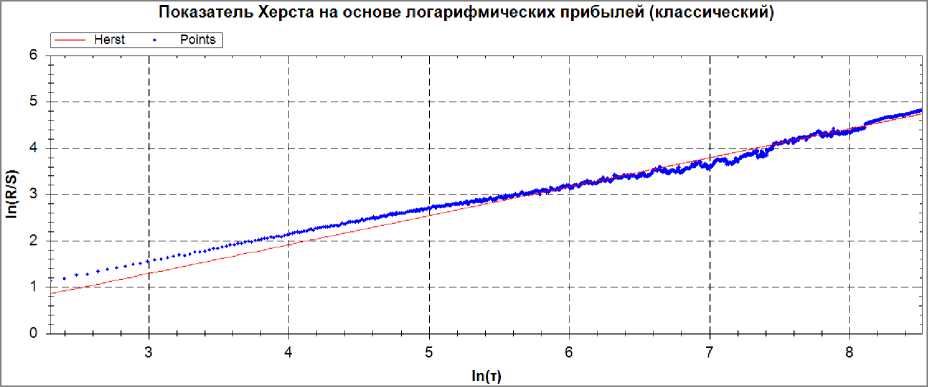
Рис. 5. Результат расчета показателя для логарифмических прибылей

В программном комплексе также предусмотрен расчет фрактальной размерности временного ряда по формуле:

D_H = 2 - H ( 1 <  D_H <  2 )

, размерности Мандельброта:

d m ⁼^г H ?

и корреляционного соотношения:

С_н = 2 2 ^{H - 1} - 1 •

Зависимость характера поведения временных рядов от величины дробной размерности и корреляционного соотношения достаточно полно представлена в [1, 3].

Заключение. Разработанное алгоритмическое и программное обеспечение дает возможность рассчитывать дробные размерности временных рядов с помощью классического и модифицированного метода. Отметим, что в случае применения классического метода ширина окон, используемых для расчета показателя Херста T ограничена величиной 2 (половиной интервала определения ряда). Модифицированный метод основан на упрощенном алгоритме. Численный эксперимент показывает, что относительная величина разности результатов, получаемых сравниваемыми методами ограничена 5%.