Сравнение методов формирования функции распределения по времени в среде моделирования GPSS для многоканальной СМО с бесконечным буфером

Автор: Галимов Р.З., Золотов А.А., Третьякова А.А.

Журнал: Форум молодых ученых @forum-nauka

Статья в выпуске: 12 (16), 2017 года.

Бесплатный доступ

В статье проведено исследование способов задания функции распределения по времени в среде моделирования GPSS. Выделены три сравниваемых подхода: по точкам, библиотечный, с помощью Гамма-функции. Рассмотрена часто встречающаяся в рамках имитационного моделирования многоканальная система массового обслуживания с бесконечным буфером. Вычислены такие показатели, как количество заявок в системе и время нахождения заявок в системе. Произведено сравнение с результатами аналитического моделирования и вычислена относительная погрешность полученных результатов.

Имитационное моделирование, задание функций, гамма-функция, библиотечные функции, функции по точкам, точность функций распределения времени

Короткий адрес: https://sciup.org/140277717

IDR: 140277717

Текст научной статьи Сравнение методов формирования функции распределения по времени в среде моделирования GPSS для многоканальной СМО с бесконечным буфером

В современном мире имитационное моделирование играет ключевую роль в анализе данных и предварительном расчете различных динамических систем. С помощью данного вида моделирования можно построить достаточно точную (в некотором приближении и с некоторыми погрешностями) модель любой сложной системы. Имитационная модель с определенной погрешностью показывает результаты функционирования реальной системы в заданных начальных условиях.

Моделирование – это метод решения задач, когда исходная (реальная) система заменяется на более простой объект, описывающий реальную систему с некоторыми допущениями, который называется моделью [2].

Имитационное моделирование применяется в различных ситуациях, например, когда эксперименты на реальной модели невозможно провести или это экономически нецелесообразно.

Имитационное моделирование – это компьютерная программа на языке имитационного моделирования (например, GPSS, Simio и др.), которая в некотором приближении описывает структуру реально существующей модели и воспроизводит ее динамическое поведение во времени.

Имитационная модель не только по свойствам, но и структуре соответствуют моделируемому объекту. Более того имеется однозначное соответствие между процессами, проходящими в имитационной модели. Существенным недостатком имитационной модели является большое время решения задачи для получения хорошей точности результатов [3].

Результатами работы модели являются значения вычисления некоторой функции от большого числа стохастически изменяющихся параметров. Как ни парадоксально, но стахастика имеет свой плюс и минус в имитационном моделировании. Элемент стохастического моделирования поведения системы оказывает положительное влияние, так как возможен разброс параметров и существует возможность получить средние или усредненные результаты. С другой стороны, требуется многократное повторение эксперимента, чтобы получился «хороший» набор экспериментальных данных. Это увеличивает время нахождения параметров функционирования системы. После проведение экспериментов обязательна обработка результатов имитационного моделирования. Чаще всего в моделях применяется статистическое моделирование, то есть воспроизведение в моделях случайных факторов, событий, величин, полей.

Стохастическое моделирование применяется в различных областях знаний и решает множество прикладных задач. Также оно применяется для исследования поведения сложных динамических систем и их последующей оценки и анализа.

В данной статье языком имитационного моделирования будет выступать язык GPSS. В языке GPSS возможно различные способы задания функций:

• Вызов нужной функции из библиотеки;
• Построение функции по точкам;
• Задание любой произвольной функции с помощью Гамма-функции.

В статье будет приведен анализ данных, полученных тремя способами задания функций, а также их сравнение с аналитическим моделированием. Будут посчитаны погрешности каждого из данных способов задания.

Смоделируем многоканальную систему с бесконечным буфером. Модель системы представлена на рис. 1.

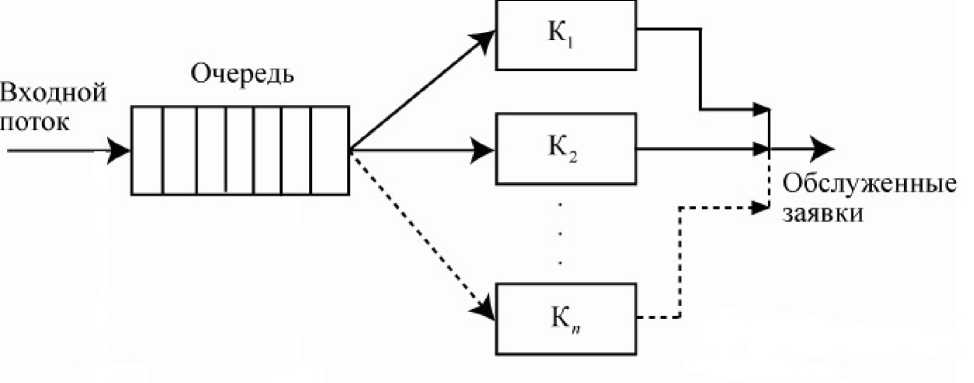
Рисунок №1. Схематическое изображение применяемой системы массового обслуживания.

Данная модель описывает широкий класс исследовательских задач и часто применяется на практике, что свидетельствует о способности корректно отображать поведение большого количества систем реального мира.

На рис.1 видно, что модель состоит из трех частей:

• Входящий поток заявок (вход системы);
• Очередь заявок на обслуживания (буфер системы);
• Обслуживающие аппараты (обслуживают заявки по заданному временному закону).

Функции распределения времени для входного потока и для обслуживания могут быть заданы различными способами, описанными выше. Рассмотрим влияние способов задания функции распределения времени и проанализируем погрешности каждого из способов задания и дадим оценку применимости того или иного способа.

Различные способы задания функций в языке имитационного моделирования

GPSS

Как отмечено выше, среда имитационного моделирования GPSS поддерживает несколько способов задания функций распределения времени [1]. Опишем более подробно вышеизложенные способы.

Задание функции распределения времени с помощью библиотечных функций

Язык имитационного моделирования поддерживают более чем десяток различных функций распределения времени. Среди них: экспоненциальная функция, функция Эрланга, биноминальная функция, нормальная функция и многие другие. Данные функции уже включены в пакет языка GPSS. Чтобы их использовать достаточно посмотреть справочник по языку GPSS, определить параметры, и функция будет работать. Это один из самых простых способов задания функций в языке имитационного моделирования GPSS.

Задание функции распределения времени по точкам

В языке имитационного моделирования GPSS также можно использовать способ задания функций распределения времени по точкам. Данный способ удобен, когда у исследователя есть точечное задание функции или функция не может быть определена формулой. Для этого вводится набор точек и далее в тексте имитационной программы вызывается данная функция. Такой способ весьма удобен при исследовании неизвестных функций распределения времени с большим набором статистических данных.

Функция, которая будет использоваться в экспериментах:

EXPON FUNCTION RN1,C23

0,0/.1,.104/.2,.222/.3,.355/.4,.510/.5,.69/.6,.915/.7,1.2/.75,1.37/.8,1.5/.84,1.83/.88,2.12/.9,2.3/.92, 2.52/.94,2.82/.95,2.98/.96,3.2/.97,3.5/.98,3.9/.995,5.3/.998,6.2/.9995,7/1,8

Задание функции распределения времени с помощью Гамма-функции

В языке имитационного моделирования GPSS также можно использовать Гамму-функцию для задания различных (произвольных) распределений. Данный способ весьма сложен, потому что требует некоторой предварительной обработки времен задания и среднего времени обслуживания. Зато данный способ подходит для моделирования любых распределений одной функцией (Гамма-функцией).

Исследование погрешности различных способов задания функций в языке имитационного моделирования GPSS

Для проведения эксперимента составим полный план эксперимента. Будем варьировать количество обслуживающих аппаратов С , а также загруженность системы р . План эксперимента представлен в таблице 1.

Таблица №1. План проводимого эксперимента

№ эксперимента	С	Р
1	1	0,2
2	2	0,2
3	3	0,2
4	4	0,2
5	5	0,2
6	1	0,4
7	2	0,4
8	3	0,4
9	4	0,4
10	5	0,4
11	1	0,6
12	2	0,6
13	3	0,6
14	4	0,6
15	5	0,6
16	1	0,8
17	2	0,8
18	3	0,8
19	4	0,8
20	5	0,8

Всего проведём 20 экспериментов. В соответствие с данным планом будет проводится имитационное моделирование для различных способов задания функций распределения времени, а также аналитическое моделирование. После этого будет проведён анализ и оценка погрешностей. За эталон будем принимать результаты аналитического моделирования.

Всего будет использоваться две основные формулы. Следующая формула определяет количество заявок в системе [5]:

L =

( К ² вар .вх + К ² обсл.вх ) Ср^с ⁺ ¹2(1 - Р ^С )

+ Ср

где L -количество заявок в системе;

К ² вар . вх - коэффициент Эрланга для входных заявок;

К ² обсл.вх - коэффициент Эрланга для процесса обслуживания;

С- количество обслуживающих аппаратов;

р - загруженность системы.

К ² вар . вх , К ² обсл.вх для экспоненциального распределения принимаем за 1.

Вычислим временя пребывания в системе [5]:

Т = L * Тх вх

, где Т – время пребывания в системе заявок;

L - количество заявок в системе;

Т_вх - расчётное время для аналитической модели.

С помощью (1,2) можно рассчитать время пребывания заявки в системе и количество заявок, находящихся в системе.

Результаты аналитического моделирования приведены в таблице 2.

Таблица №2. Результаты аналитического моделирования.

Аналитическое модели				рование
№	С	р	L	T
1	1	0,2	0,25	75
2	2	0,2	0,416667	62,5
3	3	0,2	0,604839	60,48387
4	4	0,2	0,801282	60,09615
5	5	0,2	1,00032	60,01921
6	1	0,4	0,666667	100
7	2	0,4	0,952381	71,42857
8	3	0,4	1,282051	64,10256
9	4	0,4	1,642036	61,57635
10	5	0,4	2,020692	60,62076
11	1	0,6	1,5	150
12	2	0,6	1,875	93,75
13	3	0,6	2,295918	76,53061
14	4	0,6	2,757353	68,93382
15	5	0,6	3,252949	65,05899
16	1	0,8	4	300
17	2	0,8	4,444444	166,6667
18	3	0,8	4,918033	122,9508
19	4	0,8	5,420054	101,626
20	5	0,8	5,949548	89,24322

Далее проведем 3 серии экспериментов для различного способа задания функций распределения времени. Результаты имитационного моделирования представлены в таблице 3.

Таблица №3. Результаты имитационного моделирования для различных способов задания функций распределения времени.

Исходные данные					Способ задания функции распределения времени
Исходные данные					Гамма-функция		Экспоненциальная функция		По точкам
№	С	ρ	Tвх	Tобс	L	T	L	T	L	T
1	1	0,2	300	60	0,25	75,135	0,25	75,135	0,248	74,469
2	2	0,2	150	60	0,417	62,582	0,417	62,582	0,414	62,158
3	3	0,2	100	60	0,607	60,715	0,607	60,715	0,604	60,348
4	4	0,2	75	60	0,804	60,273	0,804	60,273	0,799	59,908
5	5	0,2	60	60	1,003	60,193	1,003	60,193	0,997	59,798
6	1	0,4	150	60	0,668	100,215	0,668	100,215	0,664	99,534
7	2	0,4	75	60	0,952	71,453	0,952	71,453	0,949	71,131
8	3	0,4	50	60	1,296	64,822	1,296	64,822	1,288	64,396
9	4	0,4	37,5	60	1,665	62,438	1,665	62,438	1,654	61,976
10	5	0,4	30	60	2,041	61,267	2,041	61,267	2,032	60,916
11	1	0,6	100	60	1,506	150,611	1,506	150,611	1,498	149,616
12	2	0,6	50	60	1,869	93,584	1,869	93,584	1,865	93,156
13	3	0,6	33,3	60	2,338	77,959	2,338	77,959	2,33	77,563
14	4	0,6	25	60	2,831	70,848	2,831	70,848	2,822	70,5
15	5	0,6	20	60	3,358	67,199	3,358	67,199	3,345	66,822
16	1	0,8	75	60	4,039	303,058	4,039	303,058	4,059	303,846
17	2	0,8	37,5	60	4,414	165,698	4,414	165,698	4,439	166,132
18	3	0,8	25	60	5,027	125,841	5,027	125,841	4,987	124,503
19	4	0,8	18,75	60	5,58	104,731	5,58	104,731	5,568	104,314
20	5	0,8	15	60	6,197	93,069	6,197	93,069	6,198	92,849

Сравним полученные результаты и проведем анализ. Как уже было сказано выше, за эталон возьмем результаты аналитического моделирования и относительно них будем считать погрешность данных способов задания. Оценка погрешностей представлена в таблице 4.

Таблица №4. Оценка погрешностей между имитационным и аналитическим моделированием.

Исходные данные			Гамма-функция		Экспоненциальная функция		По точкам
№	С	ρ	ΔL,%	ΔT,%	ΔL,%	ΔT,%	ΔL,%	ΔT,%
1	1	0,2	0	0,002	0	0,002	0,008	0,007
2	2	0,2	0,001	0,001	0,001	0,001	0,006	0,005
3	3	0,2	0,004	0,004	0,004	0,004	0,001	0,002
4	4	0,2	0,003	0,003	0,003	0,003	0,003	0,003
5	5	0,2	0,003	0,003	0,003	0,003	0,003	0,004
6	1	0,4	0,002	0,002	0,002	0,002	0,004	0,005
7	2	0,4	0	0	0	0	0,004	0,004
8	3	0,4	0,011	0,011	0,011	0,011	0,005	0,005
9	4	0,4	0,014	0,014	0,014	0,014	0,007	0,006
10	5	0,4	0,01	0,011	0,01	0,011	0,006	0,005
11	1	0,6	0,004	0,004	0,004	0,004	0,001	0,003
12	2	0,6	0,003	0,002	0,003	0,002	0,005	0,006
13	3	0,6	0,018	0,019	0,018	0,019	0,015	0,013
14	4	0,6	0,027	0,028	0,027	0,028	0,023	0,023
15	5	0,6	0,032	0,033	0,032	0,033	0,028	0,027
16	1	0,8	0,01	0,01	0,01	0,01	0,015	0,013
17	2	0,8	0,007	0,006	0,007	0,006	0,001	0,003
18	3	0,8	0,022	0,024	0,022	0,024	0,014	0,013
19	4	0,8	0,03	0,031	0,03	0,031	0,027	0,026
20	5	0,8	0,042	0,043	0,042	0,043	0,042	0,04

Из таблицы видно, что погрешности минимальны и не превышают 1%. Значит все 3

способа задания распределения функции времени уместны и применимы для инженерных расчётов. Посчитаем среднюю погрешность в зависимости от загрузки системы. Для более наглядного примера построим график. График представлен на рис. 2.

Зависимость погрешности от загрузки системы

0,025

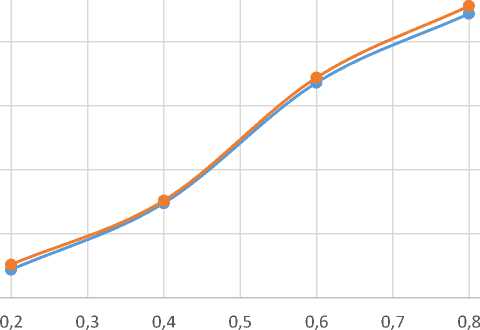
Загрузка системы

0,9

1 ■ 0,02

I CD =Г О c" 0,015 00

I—

° 0,01

a a> CL

О 0,005 c

Рисунок №2. Зависимость погрешности от загрузки системы.

Как видно из приведенного графика, погрешности в оценки количества заявок в системе и времени из пребывания в системе возрастают с ростом загрузки системы. Таким образом, точность при задании функции распределения по времени снижается при возрастании нагрузки на систему обслуживания. Однако даже при рекомендованном значении загрузки не более 75% для инженерных задач является незначительной величиной.

Из приведенного исследования видно, что погрешность между разными способами задания функций распределения времени не превышает 1%, значит они все пригодны для проведения инженерных расчетов. Разница между ними состоит в том, что каждый способ задания полезен и применим лишь в определенных условиях. Поэтому исследователь сам выбирает каким способом задания функций распределения времени пользоваться и какой способ ему удобен. Иногда данные способы взаимозаменяемые, что свидетельствует о хорошем инструменте моделирования в имитационной среде GPSS.

Список литературы Сравнение методов формирования функции распределения по времени в среде моделирования GPSS для многоканальной СМО с бесконечным буфером

Боев В. Д. Моделирование систем. Инструментальные средства GPSS World: Учеб. пособие. - СПб.: БХВ-Петербург, 2004. - 368 с.
Кирпичников А.П. Прикладная теория массового обслуживания. Казань: КГУ, 2008. 118 с.
Карташевский В.Г. Основы теории массового обслуживания. М.: Радио и связь, 2006. 107 с.
Кудрявцев Е. М. GPSS World. Основы имитационного моделирования различных систем. - М.: ДМК Пресс, 2004. - 320с.
Галимов Р.З, Золотов А.А. Исследование применимости методов аналитического и имитационного моделирования в зависимости от загруженности системы. // Молодежный научный вестник - 2017, №12 - декабрь. [Электронный ресурс]. Режим доступа: http://www.mnvnauka.ru/2017/12/Galimov.pdf

Статья научная