Сравнение общих закономерностей, характерных для структур поверхностных трещин и для напряжений в окрестности вершин пространственных трещин

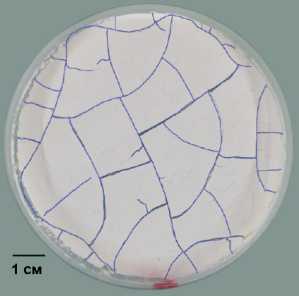
На поверхностях природных и создаваемых человеком объектов могут возникать не только одиночные трещины, но и сетки трещин. К объектам первого типа можно отнести: сланцы [1], глинистые почвы, грунты, илистые отложения при их высыхании [2–10], донья кратеров на Луне [11] и Марсе [11–13]. Ко второму типу относятся стекла [14, 15], керамика [16, 17], бетон [18], поверхность жаропрочной стали после испытания на термическую усталость [19], красочный или лаковый слой в произведениях живописи [20–22]. Типичные картины поверхностных трещин показаны на рисунке 1. Видно, что сетки трещин, вне зависимости от материала, имеют повторяющееся элементы рисунка, что привлекает внимание многих исследователей. Опубликовано большое число работ, связанных с изучением механизмов распространения трещин на поверхности разных материалов, однако до сих пор нет объяснения, почему получается тот или иной узор.

а

1 см

г

д

Рис. 1. Фотографии поверхностных трещин: треснувшая земля в Rann of Kutch (Индия) ( а ); результат лабораторного эксперимента по сушке водного раствора кукурузного крахмала [11] ( б ); поверхность высохшего солончака (Сицилия) ( в ); сеть трещин на дне ударного кратера на Марсе [26] ( г ); старая керамическая поверхность ( д ); поверхность образца из жаропрочной стали (на снимке участок размерами 320 x 240 мкм) после испытания на термическую усталость [19] ( е )

Для изучения структуры сеток поверхностных трещин широко применяется анализ цифровых изображений [23, 24] в комбинации с лабораторными экспериментами [1, 3, 4, 7, 8, 11, 19]. Помимо этого, для исследования распространения трещин часто используется метод численного моделирования [22]. Эти методы позволили определить те или иные статистические зависимости и фрактальные характеристики сеток поверхностных трещин. Интегральные функции распределения фрагментов по размеру построены в работах [2, 4, 17], функции распределения сегментов трещин по длине — в [3, 4, 17], функции распределения сегментов трещин по ширине — в [4, 7, 24], функции распределения углов между сегментами трещин — в [10, 17, 19], фрактальная размерность определена в работах [3, 6, 14, 15, 25].

При попытках найти механизмы, которые могли бы привести к построению простых моделей поведения грунтов при их высыхании и усадке, исследовано, как влияют на статистические зависимости и фрактальные характеристики структур поверхностных трещин температура [4], уровни кислотности [25] и концентрации солей [27], толщина напряжённого слоя [11].

Анализ литературы позволяет сделать вывод, что сетка трещин на поверхности материалов в основном состоит из четырёх типов фрагментов: треугольников, четырёх-, пяти- и шестиугольников, при этом наиболее распространенные пересечения линий сетки выглядят как символы Т, Y и + [3, 4, 19]. Эти формы содержат точку, в которой находится общая вершина трёх или четырёх трещин.

Пересечение трёх трещин встречается значительно чаще. В некоторых работах отмечается закономерность, а именно: углы между трещинами в основном имеют значения между 100 и 150° с пиком около 120° [10, 17, 19, 28], за пределами основного диапазона следующий пик функции распределения приходится приблизительно на 90° [2, 10, 19, 28]. Первый пик соответствует Y-конфигурации из трёх трещин, а последний пик характерен для Т- и + -конфигураций из трёх и четырёх трещин соответственно.

Трещины, как объекты исследования в рамках теории упругости, представляют интерес с точки зрения появления сингулярных решений при определении напряжённо-деформированного состояния (НДС), связанных с бесконечными значениями напряжений в вершинах и на фронтах трещин. Теоретическим обоснованием появления сингулярных решений является работа [29], где показано, что для уравнений линейной теории упругости в окрестности угловых точек имеет место решение вида ст ~ ^Kn fn rXn-1, при r ^ 0, c < ReX1 < ReX2 < < ReXn < (1) n=1

или более сложное, с логарифмическими составляющими в случае кратных точек спектра X n . Здесь: r — расстояние до угловой точки; K_n — коэффициенты интенсивности; f_n — функции углового распределения поля напряжения ст в окрестности угловой точки, в плоском случае зависящие от одной полярной угловой переменной ф (при этом c = 0), в пространственном — от двух сферических координат — ф , 9 , при c = - 0.5 .

Из решения вида (1) следует, что если имеются X n , удовлетворяющие условию Re X n <  1, то напряжения стремятся к бесконечности при r ^ 0 .

Задачам построения и приложения сингулярных решений посвящены сотни публикаций. Общую картину решений задач с особыми точками дают обзоры [30–36].

В настоящей работе представлена модель, описывающая пересечение на некоторой глубине двух, трёх, четырёх пространственных клиновидных трещин с углами раствора 90°. Приводится численный алгоритм оценки сингулярности напряжений в окрестности особых точек, обсуждаются результаты расчёта поведения напряжений и показателей сингулярности напряжений в окрестности общей вершины рассматриваемых пространственных трещин и отмечаются характерные признаки в картинах поверхностных трещин и в зависимостях поведения напряжений.

2.    Численный алгоритм анализа напряжений в окрестности вершин пространственных трещин

Идея применяемого в работе алгоритма определения степенной зависимости напряжений вблизи особых точек впервые изложена в [37] и исходит из предположения, что в достаточно малой окрестности особой точки поведение напряжений описывается одним слагаемым из представления (1). Тогда, согласно [29, 38], распределение напряжений вдоль линии, исходящей из особой точки, может быть выражено как ст = A1 rX1-1 + O (rX).

Здесь: r — расстояние от особой точки; A1 — некоторая константа, называемая коэффициентом интенсивности сингулярности; X1 — параметр, характеризующий степень сингулярности напряжений; O (rX) включает все члены с rXk, где k = 2,3, ... . При малых расстояниях r сингулярный член в уравнении (2) доминирует, и тогда это уравнение можно приближённо записать как ст ~ A1 rX1-1 или log ст = log A + (X1 - 1)log r .

В настоящей работе для определения параметра X 1 используется процедура метода конечных элементов (МКЭ) со сгущающимися к особым точкам расчётными сетками [39]. Для обнаружения зависимости (3) необходимо путём численных экспериментов найти такую дискретизацию, при которой в окрестности особой точки в ряде сеточных узлов r 1 i , r 2,..., r n , расположенных на линии, исходящей из особой точки, с приемлемой точностью выполняются соотношения:

(стА       ( r I       (ст. I       ( r I            (ст Л       ( r . I

X1 -1 ® log I — I  log I — I ® log I — I  log I — I« ... ® log I —n-1 I  log I I.

1ст2 J/     I r2 J       1стз J/     I r3 J            1стn )/     I rn )

Здесь: ст 1 , ст ₂, ^ , ст n — напряжения в узлах сетки r 1 , r ₂, ^ , r n ; X 1 — искомый показатель сингулярности напряжений. Данная зависимость позволяет вычислить значение X 1 , определяющее в окрестности особой точки поведение напряжений.

3.    Апробация алгоритма численного анализа напряжений в окрестностях особых точек

Описанный в разделе 2 алгоритм апробирован для различных типов особых точек в двумерных задачах, где наименьшее собственное значение является действительным числом [39]. В рассмотренных двумерных задачах отличие показателей сингулярности, найденных с помощью данной численной процедуры, от рассчитанных аналитически составляет не более 0.08%.

Для иллюстрации дополнительных аргументов в пользу достоверности результатов, полученных на основе численного алгоритма, в качестве примера возьмём трёхмерную задачу, связанную с определением поведения напряжений в вершине трещины, фронт которой перпендикулярен поверхности O xy (Рис. 2 а ). Сингулярность напряжений оценим в точке О. Контур сферы на рисунке 2 a представлен только для визуализации трещины в упругом полупространстве. В работе [40] эта задача решена численно, рассчитаны показатели сингулярности напряжений для изотропного и трансверсально-изотропного материалов (упругие характеристики см. в таблице 1).

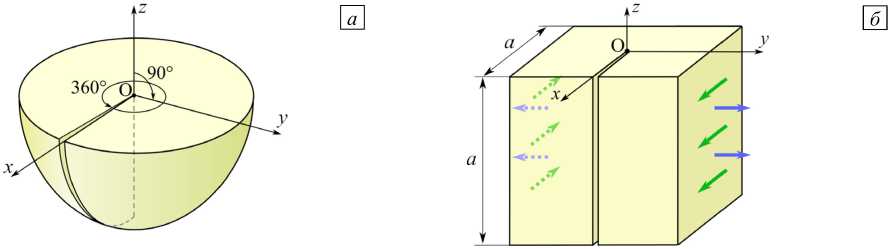
Рис. 2. Трещина, фронт которой перпендикулярен поверхности упругого полупространства ( а ) и соответствующая расчётная схема ( б )

Таблица 1. Упругие характеристики материала [40]

Материал	Ei , МПа	Gij , МПа	v i
Изотропный	21000		0.3
Трансверсально-изотропный	Er = 130300, E = E = 9377 x       yz	G xy = G xz = 4502 , G yz = 2865	v xy =v xz =v yz = 0.33

При использовании численного алгоритма в качестве расчётной схемы вместо упругого полупространства возьмём куб, размер граней которого в рассматриваемой задаче не имеет значения (Рис. 2 б ). При этом условия нормального разрыва трещины реализуются при задании на боковых гранях, параллельных плоскости O xz , нормальных перемещений, а условия поперечного сдвига — при задании на этих же боковых гранях касательных перемещений, направленных параллельно оси O x и противоположно относительно друг друга.

В таблице 2 для трещины в условиях нормального разрыва и поперечного сдвига представлены показатели сингулярности напряжений из работы [40] и рассчитанные согласно предлагаемому численному алгоритму, основанному на выделении из КЭ-решения асимптотики напряжений в соответствии с соотношениями (4). Отличие показателей сингулярности, полученных этими двумя методами, составляет не более 1.5%.

Таблица 2. Показатели сингулярности напряжений для трещины, фронт которой перпендикулярен поверхности упругого полупространства

Материал	X j (поперечный сдвиг)		X 2 (нормальный разрыв)
	Численный алгоритм	[40]	Численный алгоритм	[40]
Изотропный	0.40	0.3929	0.55	0.5483
Трансверсально-изотропный	0.46	0.4543	0.52	0.5227

4.    Результаты численных экспериментов

Для расчёта НДС в окрестности вершины нескольких пересекающихся трещин применялся МКЭ. Достоверность численных результатов обеспечивалась за счёт построения конечно-элементных сеток, сгущающихся к точке пересечения фронтов трёхмерных трещин, и выбором на основе численных экспериментов степени дискретизации, дающей необходимую точность решения. В качестве таких дискретизаций использовались конечно-элементные сетки, на которых выполнение естественных краевых условий вне трёх–четырёх элементов, примыкающих к особой точке, достигалось с погрешностью не более 1%.

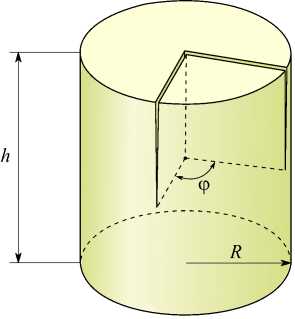
В качестве первого примера рассмотрена задача, в которой две поверхностные трещины пересекаются под углом ϕ (Рис. 3 а ) и представляются как клиновидные математические разрезы с углом раствора 90°. Прямой угол выбран для того, чтобы глубина проникания трещин была одинаковой. В качестве расчётной схемы взят цилиндр (см. Рис. 3 б ). К боковой поверхности цилиндра приложено нормальное растягивающее усилие σ ₀ . Вычисления выполнены при разных величинах угла ϕ и следующих значениях параметров: hR = 6 ; общая вершина находится на глубине hR = 1 от верхнего торца цилиндра, коэффициент Пуассона материала ν= 0.3 .

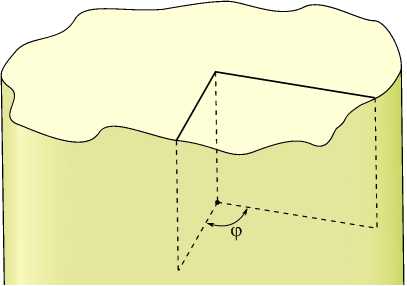
Рис. 3. Пересечение двух поверхностных трещин ( а ) и расчётная схема ( б )

б

Для сравнения НДС вблизи вершины трещины можно использовать коэффициент интенсивности напряжений (КИН). Но, поскольку при варьировании угла ϕ геометрия вблизи общей вершины фронтов двух трещин меняется, переменной будет и размерность КИН. Сопоставлять же КИН с разными размерностями некорректно. Поэтому для сравнения НДС вблизи общей вершины фронтов нескольких трещин при разных углах ϕ удобнее использовать энергетическую характеристику — плотность энергии деформаций. Значения средней плотности энергии деформаций вычислены в фиксированном объёме малой сферы, центр которой размещается в общей вершине фронтов трещин и совпадает с началом прямоугольной системы координат O xyz . Ось O y направлена по оси цилиндра.

На рисунке 4 показана сфера из 2560 конечных элементов. Радиус сферы составляет 10 ^{- 3} R . Для иллюстрации на рисунке 5 приведены зависимости от угла ϕ средней плотности энергии деформаций

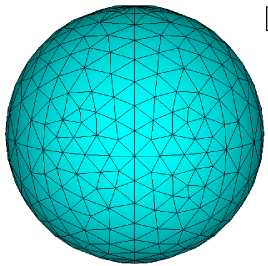
а

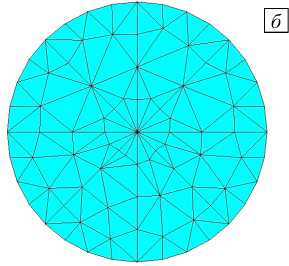
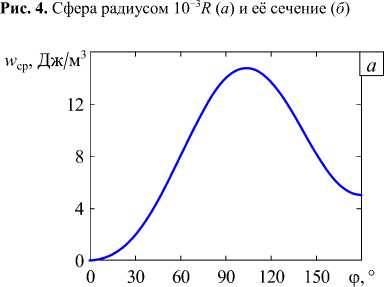
Рис. 5. Зависимость от угла ϕ средней плотности энергии деформаций между двумя трещинами: в сфере радиусом 10 ^{- 3} R ( а ); в сфере радиусом 5 ⋅ 10 ^{- 4} R ( б )

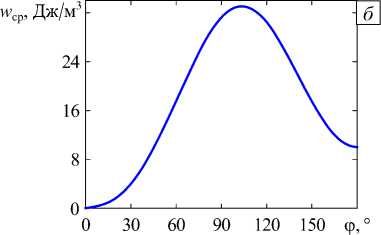
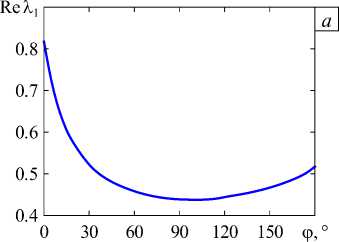
Рис. 6. Зависимость Re Х 1 от угла ф между двумя трещинами ( а ); распределение главных напряжений с 1 /о ₀ вдоль оси цилиндра в направлении от общей вершины при разных значениях угла ф ( б )

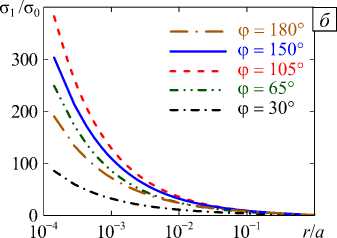
w _cp для сферы радиусом 10 ³ R и 5 - 10 4 R , а на рисунке 6 а — зависимость от угла ф собственных значений Х 1 , полученных с помощью численного алгоритма, основанного на выделении из КЭ-решения асимптотики напряжений в соответствии с соотношениями (4). В силу симметрии задачи результаты представлены до значения ф = 180 ° . В качестве дополнительной информации на рисунке 6 б для некоторых

Рис. 7. Трещины на поверхности бетона с изломами под углом ~100–110° (см. кружки)

значений угла ф показаны распределения главных напряжений о 1 вдоль оси цилиндра в направлении от общей вершины.

Из проведённых расчётов установлено, что максимумы средней плотности энергии деформаций в сфере при обоих радиусах располагаются между 100 и 110°, что позволяет говорить о том, что при угле из этого диапазона излом трещины наиболее вероятен. Вывод хорошо согласуется с картиной ломаной трещины на поверхности бетона (Рис. 7). Следует отметить, что при ф ^ 0 результаты для двух клиновидных трещин с углами раствора 90° приближаются к результатам для одной клиновидной трещины с углом раствора 90° как по величине средней плотности энергии деформаций, так и по значению показателя сингулярности напряжений Х1. Сопоставив рисунки 5 и 6б, можно сделать вывод, что максимуму средней плотности энергии деформаций и максимальной концентрации напряжений отвечает одинаковый угол ф .

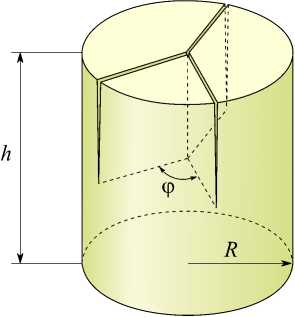
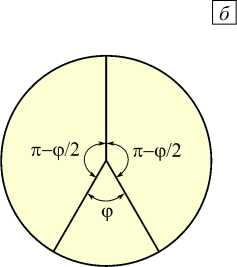
По аналогии с исследованием НДС в окрестности общей вершины двух пересекающихся трещин осуществлены численные эксперименты для различных конфигураций пересечения трёх и четырёх пространственных трещин. Для трёх трещин рассмотрены две конфигурации: Y (Рис. 8–10) и T (Рис. 11–13), а для четырёх трещин — Х-конфигурация (Рис. 14–16). Геометрия конфигураций определяется углами между берегами соседних трещин. Для Y-конфигурации два угла равны ( п-ф/ 2 ) и зависят от величины третьего угла — угла ф (Рис. 8 б ). В T-конфигурации один угол между трещинами всегда п , второй — ф , а третий — ( п-ф ) (Рис. 11 б ). Конфигурация X характеризуется двумя парами смежных углов. В одной паре углы равны ф , а в другой — ( п-ф ) (Рис. 14 б ).

а

Рис. 8. Расчётная схема пересечения трёх трещин (Y-конфигурация) ( а ) и вид сверху на торец цилиндра ( б )

Как и в задаче для двух трещин, при трёх трещинах в качестве расчётной схемы взят цилиндр, представленный рисунках 8 а, 11 а и 14 а . К боковой поверхности цилиндра приложено нормальное растягивающее усилие σ ₀ . Расчёты выполнены при разных ϕ и следующих параметрах: hR = 6 , коэффициент Пуассона материала ν = 0.3. Для всех названных конфигураций вычислены зависимости от угла ϕ средней плотности энергии деформаций (Рис. 9, 12, 15) и собственных значений λ ₁ (Рис. 10 а , 13 а , 16 а ), полученных с помощью численного алгоритма, основанного на выделении из КЭ-решения асимптотики напряжений в соответствии с соотношениями (4). Дополнительно для некоторых значений угла ϕ построены распределения главных напряжений σ ₁ вдоль оси цилиндра в направлении от общей вершины (Рис. 10 б , 13 б , 16 б ).

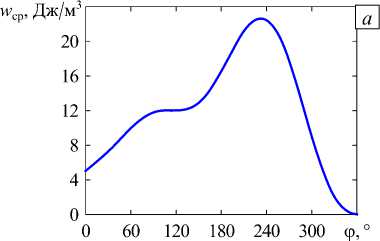
Рис. 9. Зависимость от угла φ средней плотности энергии деформаций при Y-конфигурации: в сфере радиусом 10 ^{- 3} R ( а ); в сфере радиусом 5 ⋅ 10 ^{- 4} R ( б )

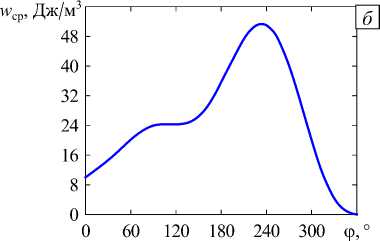
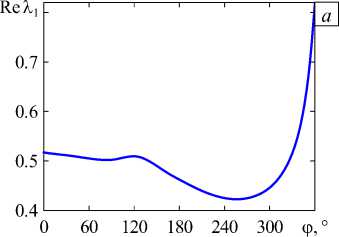
Рис. 10. Зависимость Re λ ₁ от угла ϕ для Y-конфигурации трёх трещин ( а ); распределение главных напряжений σ ₁ σ ₀ вдоль оси цилиндра в направлении от общей вершины при различных значениях угла ϕ ( б )

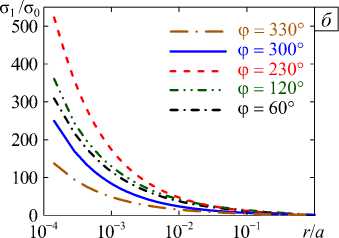
Проведённые расчёты позволили установить, что при Y-конфигурации локальные максимумы средней плотности энергии деформаций для сферы обоих радиусов располагаются между 110 и 115°. Это совпадает с наблюдаемой закономерностью, заключающейся в том, что углы между трещинами в основном лежат в диапазоне между 100 и 150° с пиком около 120° [10, 17, 19, 28]. Однако глобальным максимумам при обоих радиусах отвечают углы со значениями между 225 и 235°, и соответствующие им Y-конфигурации в картинах реальных сеток трещин не встречаются. Уровень средней плотности энергии деформаций, близкий к локальному максимуму и больший, характерен для угла ϕ от 100 до 290°, при этом два других угла ( π-ϕ I 2 ) будут находиться в диапазоне от 130 до 35°. Из сопоставления

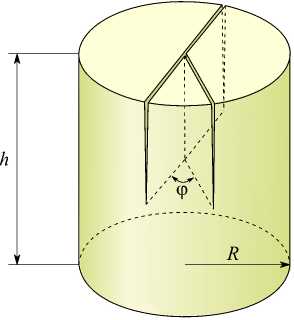
Рис. 11. Расчётная схема пересечения трёх трещин (T-конфигурация) ( а ) и вид сверху на торец цилиндра ( б )

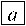
б

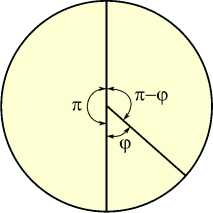
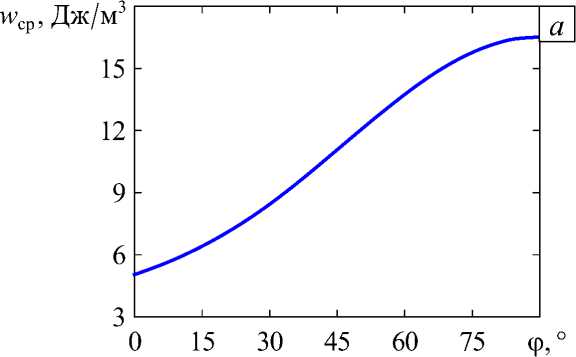
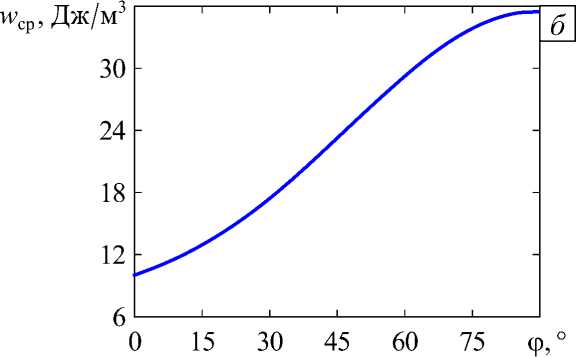
Рис. 12. Зависимости от угла ф средней плотности энергии деформаций при T-конфигурации в сфере радиусом 10 ³ R ( а ) и радиусом 5 - 10 " ⁴ R ( б )

ReX]

0.51 И

0.5 -

0.49 -

0.48 -

0.47 -

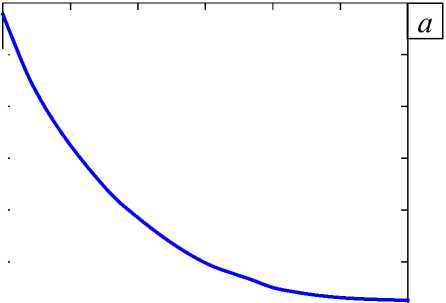
0.46-----------1-----------1-----------1-----------1-----------1-----------

0    15   30   45   60   75 ф,

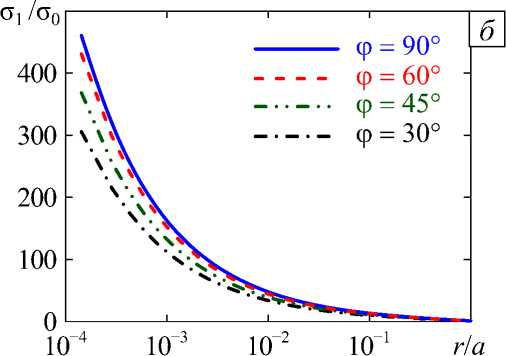
Рис. 13. Зависимость от угла ф величины Re Х 1 для трёх трещин (T-конфигурация) ( а ); распределения главных напряжений с 1 /с₀ вдоль оси цилиндра в направлении от общей вершины при разных значениях угла ф ( б )

результатов на рисунках 9 и 10 б следует, что обнаруженная для двух трещин качественная корреляция между средней плотностью энергии деформаций и асимптотикой главных напряжений вблизи общей вершины трёх трещин также имеет место и для Y-конфигурации.

В силу симметрии T-конфигурации результаты на рисунках 12 и 13 представлены до значения ф = 90 ° . Видно, что максимумам средней плотности энергии деформаций в сфере при обоих радиусах отвечает угол ф = 90 ° (то есть симметричная T-конфигурация). Именно она встречается в картинах сеток поверхностных трещин [3, 4, 11, 19, 27] (см. Рис. 1 б ). Сопоставление результатов на рисунках 12 и 13 позволяет сделать вывод, что и для Т-конфигурации свойственна качественная корреляция между средней плотностью энергии деформаций и асимптотикой главных напряжений вблизи общей вершины.

При пересечении четырёх трещин с X-конфигурацией (Рис. 14) в силу симметрии последней результаты на рисунках 15 и 16 представлены до ф = 90 ° . Проведенные расчёты позволили установить, что максимумы средней плотности энергии деформаций для сферы обоих радиусов и наименьшее значение показателя сингулярности располагаются при угле ф = 90 ° (когда все углы между четырьмя трещинами равны), что также совпадает с наблюдаемой закономерностью, заключающейся в том, что четыре трещины чаще сходятся под углом примерно 90° [2, 10, 19, 28]. Сопоставив рисунки 15 и 16, можно сделать вывод, что и для X-конфигурации имеет место качественная корреляция между средней плотностью энергии деформаций и асимптотикой главных напряжений вблизи общей вершины.

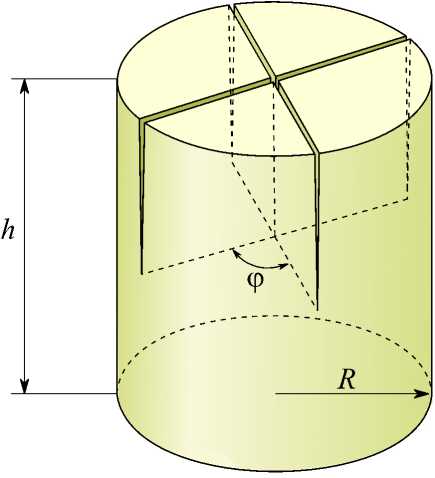
Рис. 14. Расчётная схема пересечения четырёх трещин (X-конфигурация) ( а ) и вид сверху на торец цилиндра ( б )

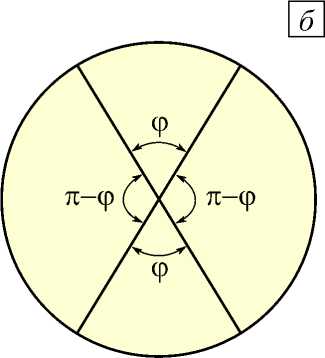
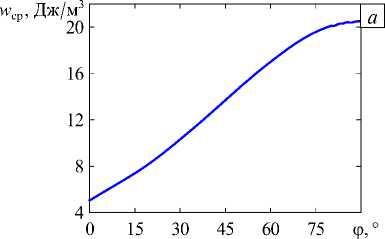
Рис. 15. Зависимость средней плотности энергии деформаций от угла ф для четырёх трещин в сфере с радиусом 10 ³ R ( а ) и

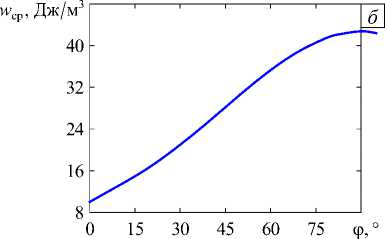
в сфере с радиусом 5 - 10 -4 R ( б )

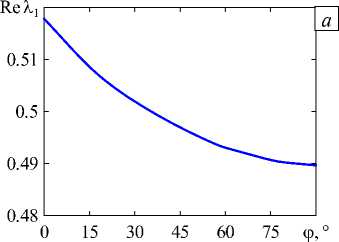
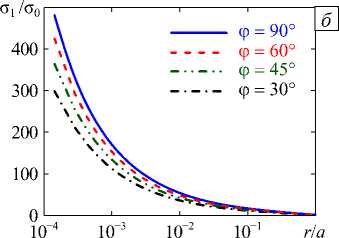
Рис. 16. Зависимость Re Х 1 от угла ф для X-конфигурации четырёх трещин ( а ); распределения главных напряжений п /О о

вдоль оси цилиндра в направлении от общей вершины при различных значениях угла ф ( б )

5.    Заключение

Проведено сопоставление результатов численного моделирования пересечения двух, трёх, четырёх трещин на поверхности изотропного полупространства с реальными картинами сеток поверхностных трещин. Представлен численный алгоритм анализа напряжений в окрестности особых точек в трёхмерных телах. Разработанный алгоритм апробирован для различных типов особых точек в двумерных задачах и в трёхмерной задаче, связанный с оценкой поведения напряжений в точке выхода на поверхность перпендикулярного ей фронта одиночной пространственной трещины.

Продемонстрировано, что алгоритм позволяет рассчитать показатели сингулярности напряжений в общей вершине пространственных трещин. Для двух трещин, пересекающихся под углом ф , обнаружена корреляция между величиной угла излома линии сетки трещин на поверхности и значением угла ф , при котором достигается максимум средней плотности энергии деформаций в малой сфере, центр которой расположен в общей вершине. Для трёх трещин рассмотрены две наиболее распространённые конфигурации: Y и T.

Установлено, что для T-конфигурации максимуму средней плотности энергии деформаций и наименьшему значению показателя сингулярности отвечает угол ф = 90 ° , что полностью соответствует симметричной T-конфигурации, встречающейся в реальных картинах поверхностных трещин. В случае Y-конфигурации глобальный максимум средней плотности энергии деформаций и наименьшее значение показателя сингулярности достигаются при определяющих конфигурацию значениях угла ф , которые не присутствуют в реальных картинах поверхностных трещин. Однако диапазон изменения угла 100 < ф <  290 ° , для которого характерен высокий уровень средней плотности энергии деформаций, полностью содержит в себе углы от 100 до 150°, присущие Y-конфигурациям реальных трещин.

Для X-конфигурации из четырёх трещин выявлено, что максимум средней плотности энергии деформаций и наименьшее значение показателя сингулярности имеют место, когда все углы между четырьмя трещинам равны. Это также совпадает с наблюдаемой в реальных картинах трещин закономерностью, что четыре трещины чаще сходятся под углом около 90°, то есть в симметричной + -конфигурации.

Во всех приведённых в работе задачах обнаружена прямая зависимость между средней плотностью энергии деформаций и асимптотикой главных напряжений вблизи общей вершины пространственных трещин.

Работа выполнена при финансовой поддержке РФФИ и Пермского края (проект № 20-41-596007).