Сравнение оптимальных режимов водогазового воздействия в рамках одномерной и двумерной постановок задачи фильтрации

Для повышения нефтеотдачи пластов применяют различные методы, например, закачивают в них воду и/или газ. Вода действует как поршень и способствует движению нефти к добывающим скважинам. Газ может растворяться в нефти и тем самым снижать ее вязкость и увеличивать объем. К хорошо растворяющимся в нефти газам относится углекислый газ (СО2) [1, 2]. Помимо этого, СО2 является парниковым газом, поэтому для решения проблемы глобального потепления актуально уменьшение его выбросов в атмосферу. Одной из мер декарбонизации служит улавливание и захоронение CO2 в нефтяных пластах [3–5]. Для того чтобы увеличить добычу нефти, необходимо определить, какие режимы водогазового воздействия на нефтяные пласты являются оптимальными.

Цель этого исследования — во-первых, понять, как меняется расчетная эффективность закачки при переходе от 1-D к 2-D гидродинамическому моделированию площадной разработки месторождений, во-вторых, выяснить, можно ли для расчета оптимальных режимов водогазового воздействия ограничиться только 1-D моделированием. Для сравнения рассматриваются результаты исследования оптимальных режимов водогазового воздействия в рамках 1-D постановки задачи, ранее представленные в [6].

Выбор наилучшего варианта системы разработки нефтяного месторождения и оценка эффективности водогазового воздействия осуществляются по коэффициенту охвата залежей вытеснением. Коэффициент

охвата вытеснением определяется как отношение нефтенасыщенного объема пласта, охваченного процессом вытеснения, ко всему нефтенасыщенному объему этого пласта в выбранном условном расчетном контуре [7]. В численном моделировании фильтрации коэффициент охвата представляется в виде:

NM Kохв =E Vdr Vj, где V и V — поровые дренируемые и общие нефтенасыщенные объемы расчетных ячеек с номерами i и j , N — число дренируемых ячеек, а M — общее число ячеек. Считаем, что ячейка дренируется — «охвачена вытеснением», если в течение какого-либо расчетного времени значение насыщенности закачиваемой воды (или газа) увеличивается на 0,05. В соответствии с определением, Ктв =1 в 1-D моделировании и Ктв < 1 в 2-D моделировании. Таким образом, сравнение 1-D и 2-D моделирования направлено на оценку влияния коэффициента на расчетные оптимальные режимы водогазового воздействия.

Известно (см. [8]), что неоднородность среды влияет на охват пласта вытеснением, так как низкопроницаемые включения мешают движению жидкости или газа. В этом случае могут образовываться дополнительные области, не охваченные вытеснением, что приведет к снижению коэффициента охвата. В данной работе такие эффекты не учитываются, предполагается, что пористая среда является однородной, то есть значения пористости и проницаемости одинаковы во всех точках пласта.

2.    1-D и 2-D постановки задач

Рассмотрим изотермическое одномерное течение в области 0 < x < L однородной пористой среды, которая насыщена углеводородной смесью, состоящей из трех компонентов: CH 4 , C 6 и C 16 (Рис. 1 а ). Здесь C₆ и C₁₆ — углеводородные соединения (алканы), имеющие шесть и шестнадцать атомов углерода соответственно. Предполагаем, что углеводородная смесь состоит из 20% CH₄, 40% C₆ и 40% C₁₆. Далее моделируем фильтрацию, связанную с закачкой в пласт СО₂, который может в значительных объемах растворяться в нефти. Таким образом, далее исследуется фильтрация четырехкомпонентной смеси СО 2 -СН 4 -С 6 -С 16 . В начальный момент времени t = 0 распределения давления P _Q = 13,9 МПа, температуры T = 93°C и полных мольных концентраций компонентов смеси z = { 0; 0,2; 0,4; 0,4 } однородные.

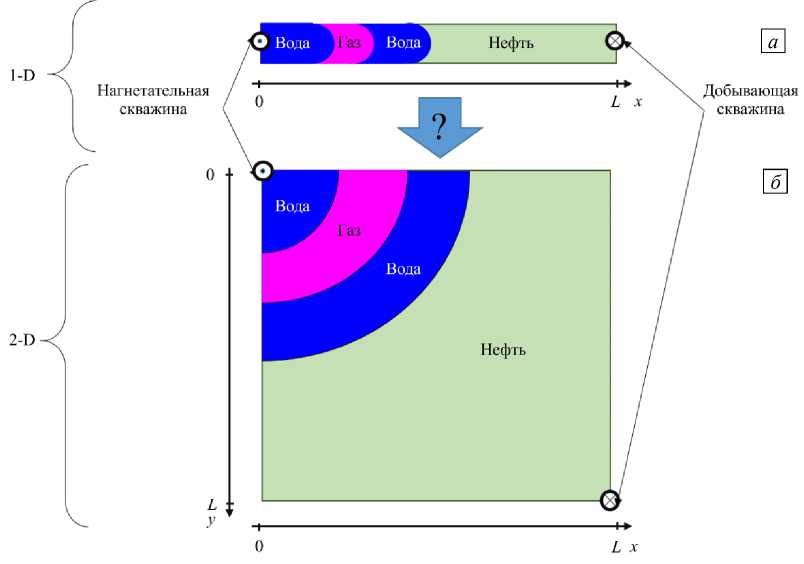
Рис. 1. Схема к постановке задачи

Вытеснение нефти моделируется на примере двух источников, размещенных в точках с координатами x = 0 (нагнетательная скважина) и x = L (добывающая скважина), которые открываются при 1 = 0. Нагнетательная скважина работает при постоянном объемном расходе Q , который задается исходя из пластовых давления и температуры для любой вытесняющей жидкости. Добывающая скважина работает при постоянном забойном давлении, равном начальному пластовому давлению P .

Обсудим четыре основных стратегии закачки. Во-первых, положим, что нефть вытесняется путем закачки воды. Эта стратегия, обозначаемая символом W, соответствует заводнению, применяемому в качестве вторичного метода извлечения нефти. Вторая стратегия — это непрерывная закачка CO2; она обозначается символом G. Следующие две стратегии предполагают поочередную подачу воды и газа. Так, при стратегии WG сначала в течение определенного периода времени нагнетается вода, а затем газ. Стратегия GW представляет собой обратную к W+G последовательность: первым закачивается газ, а затем вода.

По аналогии с одномерным течением рассмотрим двумерное течение в области 0 < x < L, 0 <  y <  L однородной пористой среды (Рис. 1 б ). Параметры среды возьмем такие же, как и в одномерной задаче, а вытеснение нефти будем моделировать с помощью источников, размещенных в точках с координатами (0, 0) (нагнетательная скважина) и ( L , L ) (добывающая скважина) и открывающихся в момент 1= 0 . Такое расположение отвечает пятиточечной схеме расстановки скважин [9]. Подобная система представляет собой квадрат, в углах которого находятся добывающие скважины, а в центре — скважина нагнетательная. В силу симметрии размещения скважин проанализируем фильтрацию только в одном квадратном элементе. Для него отношение нагнетательных и добывающих скважин составляет 1:1, при этом нагнетательная и добывающая скважины располагаются в его противоположных углах

Используем стандартную композиционную модель, описывающую течение жидкости и газа в пористых средах [6]. Считаем, что течение изотермическое, капиллярное давление равно нулю. Основные уравнения фильтрации имеют вид:

• ⁵ 1 ( ^Ф ( р g c g ( i ) s g +Р o c o ( i ) s o ) ) ^{+ V} " ( p g c g ( i ) u g +P o c o ( i ) u o ) = ^{0 (} i = 1,..,⁴⁾ , ⁽¹⁾

5t (фр wsw ) + V-(P wuw ) = 0 , (2)

K u =-K — VP (j = g, w, o), (3) Pj где 5, =5/51, ф — пористость, р — плотность, с^ — массовая концентрация i -го компонента в j -й фазе, s — насыщенность, u — вектор скорости фильтрации, K — абсолютная проницаемость пористой среды, K — относительная фазовая проницаемость, р — динамическая вязкость. Индексы g , o и w обозначают, соответственно, параметры газа, нефти и воды. Уравнения (1) и (2) — это законы сохранения массы i -го компонента углеводородной смеси и воды, а уравнение (3) есть закон Дарси.

Для расчета парожидкостных равновесий в системе CO 2 –CH 4 –C 6 –C 16 используем кубическое уравнение состояния Соаве–Редлиха–Квонга с коррекцией объемов [10, 11]. Из решения уравнения состояния определим параметры р ,, с^ и s_y для газа и нефти ( j = g , o ), а также количество фаз в системе для заданных P , T и z . Вязкость рассчитаем с помощью корреляций Лоренца–Брэя–Кларка [12]. Параметры воды считаем постоянными: p_w и p_w= 0,35 сП. Для других величин возьмем значения: сжимаемость скелета пористой среды равна 0; ф= 0,1 ; K_x = K = 10⁵ мД; L = 100 м; расход Q = const , но различен в разных расчетах.

Согласно закону Дарси, давление P обратно пропорционально проницаемости K , поэтому вследствие большого значения проницаемости оно незначительно отклоняется от начального значения P и не влияет на парожидкостные равновесия. Используем корреляции Кори [13] для относительной проницаемости двухфазных течений вода–нефть и газ–нефть:

2 К ($ 1 = s w - swc K w ( s w )    1 1           1 V    1   s wc J (     s„ K g ( ■ > = 0-74li g V 1    s wc

,25                                                         2,75 ,      K row ( S w ) = 0,8 | 1 - s w - s or I    , 1 — s — s V      wc    or J                                     (4) 1,8                                                           2,75 )        K  /  if 1— s g — s wc — s or ) J ,         rog ( g )    V    1 — S wc — S or   J     ,

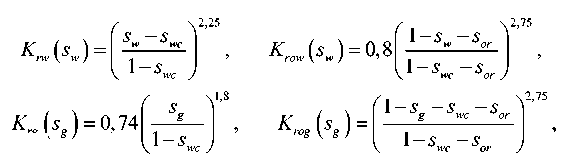
где ^s w_с= 0,16 — неснижаемая насыщенность воды, s_or= 0,24 — остаточная насыщенность нефти. Коэффициенты в уравнениях (4) выберем в соответствии с кривыми относительной фазовой проницаемости, используемыми в [14]. Применим усредненное по объему приближение для относительной проницаемости нефти в трехфазном течении:

Kro

'w - s wc ) K row ( s w ) + s g K rog

(sg ))/(sw - swc - sg ) .

Композиционное моделирование в рамках численного решения конечно-разностных аналогов уравнений (1)–(3) проведем с помощью гидродиномического симулятора MUFITS [15]. В связи с необходимостью сопряжения расчета гидродинамики углеводородной смеси со сложными термодинамическими расчетами ее парожидкостных равновесий 2-D моделирование требует значительных вычислительных ресурсов. Вследствие этого существенно замедляются расчеты оптимальных параметров водогазового воздействия, которые требуют выполнения нескольких десятков композиционных расчетов фильтрации. Для ускорения процесса счета применим гибридный метод оптимизации, использующий как стохастические, так и градиентные алгоритмы и предполагающий построение последовательности композиционных моделей возрастающей сложности [16]. Критерием оптимальности режимов является максимальная экономическая прибыль, то есть чистая приведенная стоимость — Net Present Value (NPV * ).

Введем целевую функцию J :

J =

NPV * = j

C

( 1 + D ) ‘‘"d*

dt ' ,

где D — ставка дисконтирования (процентная ставка, используемая для пересчета будущих потоков доходов в единую величину текущей стоимости), t — период дисконтирования [17, 18]. Параметр C определяется как разность между доходами с продажи нефти ( rq ) и расходами на закачку воды ( rq ) и газа ( rq ), а также в дальнейшем на их сепарацию и утилизацию ( rq и rq ): C = r_oq_o - r wi q wi - r wp q wp - r gi q gi - r gp q gp , где r — стоимость единицы массы закачиваемых, добываемых и утилизируемых компонентов, а q — их массовый расход. Числовые значения параметров r указаны в работе [6]. Параметр r — чистая прибыль от продажи нефти, которая зависит как от рыночной цены нефти, так и параметров налогообложения. Современный диапазон рыночных цен 60–80 $/баррель соответствует значению r в диапазоне 10–20 $/баррель.

Для масштабирования результатов моделирования удобнее обезразмерить соотношение (5) и привести его к следующему виду [6]:

PVI

NPV ( PVI ) = j ^— exp ( V Q ) ^{V ( PVI )} d ( PVI' ) ^ max , ^{0 r} o ^Q

где Q =------ ds ---- = const — безразмерная скорость закачки, V,  — объем порового пространства,

VhC log (1 + D)                                                         hc занятого нефтью в момент t = 0, PVI — количество закачанных поровых  объемов, а NPV = NPV*/(rV с) — безразмерная чистая приведенная стоимость закачки. Таким образом, необходимо найти такое значение закачанного объема, при котором значение NPV максимально.

• 3.    Результаты

  • 3.1.    Сравнение результатов 1-D и 2-D моделирования

Проведем сравнение результатов расчета эффективности закачки газа в рамках 1-D и 2-D постановок задачи. Подробное исследование на основе одномерной модели содержится в работе [6]. Рассчитаны оптимальные стратегии при различных скоростях закачки Q . Рассмотрим рисунок 2, где штриховые линии соответствуют одномерной постановке задачи. Наибольшие значения NPV достигаются при высоких скоростях закачки. При снижении Q значения NPV уменьшаются. Так, оптимальной стратегией при высокой скорости закачки ( 1J Qe [ 0; 0,6 ] ) является стратегия GW. Далее, при понижении скорости закачки, наилучшей становится стратегия WG.

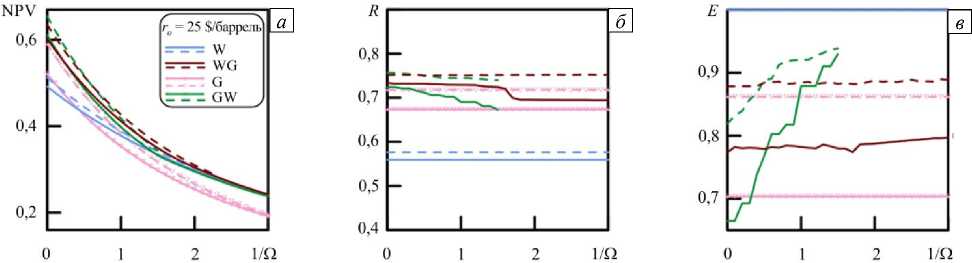
Рис. 2. Эволюция чистой приведенной стоимости ( NPV ) ( а ), коэффициента извлечения нефти ( R ) ( б ) и коэффициента захоронения CO 2 ( E ) при различных стратегиях и условии, что r_o = 25 $/баррель; штриховые линии отвечают 1-D постановке, сплошные линии – 2-D постановке

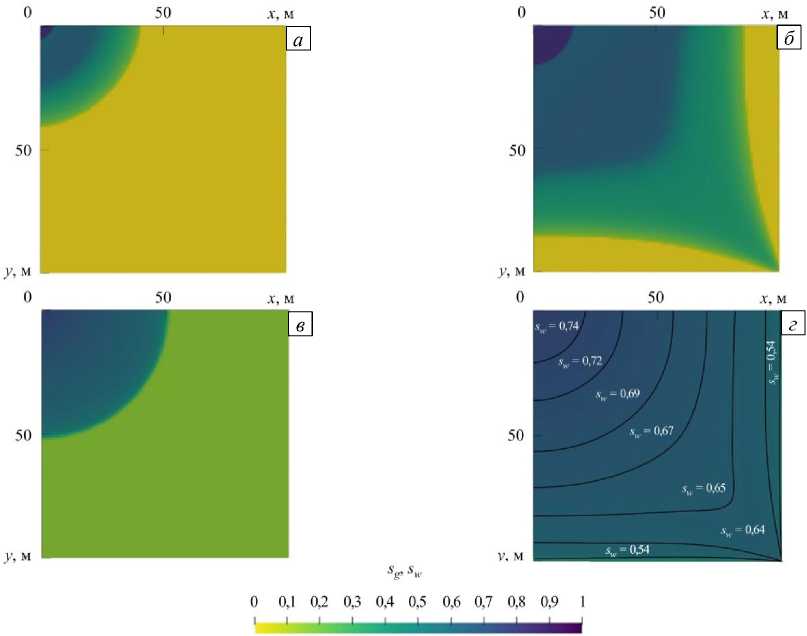
Рис. 3. Распределение насыщенности CO 2 в стратегии G ( а , б ) и воды в стратегии W ( в , г ) при П= 0,5 в различные моменты времени: PVI = 0,074 ( а , в ) и PVI = 1,227 ( б , г )

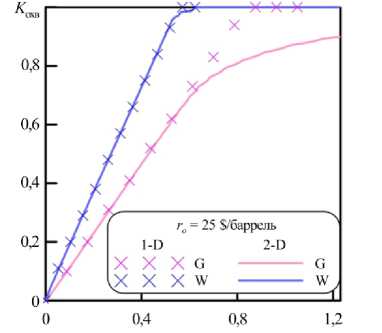
Рис. 4. Коэффициент охвата нефти при непрерывной закачке CO 2 и воды (стратегии G и W)

Перейдем к рассмотрению 2-D случая. При малых временах фронт вытеснения распространяется осесимметрично рядом с нагнетательной скважиной (Рис. 3). Далее, при приближении к добывающей скважине, фронт вытягивается, а вдоль границ x = L и y = L остаются не охваченные вытеснением области. При этом газ растворяется в нефти, снижает ее вязкость и вместе с ней перемещается к добывающей скважине. Вода, действуя как поршень, способствует движению нефти также к добывающей скважине, поэтому коэффициент охвата нефти для стратегии W больше, чем для стратегии G (Рис. 4). При стратегии G в 2-D случае он остается меньше единицы, в отличие от 1-D случая, где вытеснением охвачен весь объем породы и коэффициент охвата нефти равен 1. Согласно определению, коэффициент охвата является монотонно возрастающей функцией времени. В 1-D случае при закачке газа K изменяется от 0 до 1, в 2-D случае — от 0 до 0,9 (Рис. 4). При стратегии W значения K достигают единицы как в 1-D, так и в 2-D случае. Следовательно, параметры NPV , эффективность захоронения CO2 ( E ) и коэффициент извлечения нефти ( R ) имеют большую величину, то есть кривые, соответствующие 1-D случаю, лежат выше, чем кривые для 2-D случая (см. Рис. 2).

• 3.2.    Влияние цены нефти на оптимальную стратегию

Экономическая ситуация в мире постоянно меняется, и рыночная цена нефти нестабильна. Поэтому с целью выявления оптимальных стратегий проведена серия расчетов при различных значениях r : 6,25; 9; 18; 25; 50 $/баррель. На основе полученных результатов построена карта стратегий. Рассмотрим 1-D случай (Рис. 5 а ): низкие значения r отвечают стратегии W, так как закачка воды требует меньших расходов, чем закачка CO 2 . Более высокие значения r , например т_о = 50 $/баррель, соответствуют стратегиям GW при 1/ О е [ 0; 0,3 ] и WG при 1) О е [ 0,3; 3 ] .

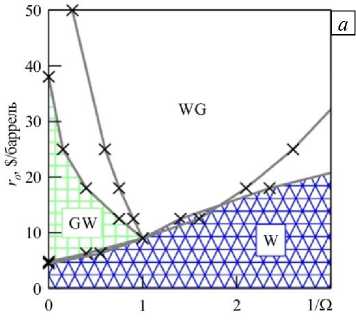
Рис. 5. Карта оптимальных стратегий в 1-D ( а ) и 2-D ( б ) случаях при различных значениях r_o и О

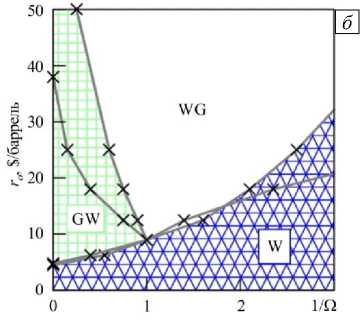
В 2-D случае (Рис. 5 б ) область, соответствующая стратегии WG, имеет большую площадь, чем в 1-D случае. Большие значения r_o и высокие скорости закачки О отвечают оптимальной стратегии WG, то есть закачке воды с последующей закачкой газа. Далее, при уменьшении площади WG на карте, уменьшается и r , а при высокой скорости закачки оптимальной становится стратегия GW. Дальнейшее снижение скорости закачки делает оптимальной стратегию W. Итак, при понижении цены нефти оптимальной является стратегия с закачкой воды как в 1-D, так и в 2-D случаях. Как видно из рисунка 5, области оптимальных стратегий в обоих случаях имеют качественно одинаковый вид.

• 3.3.    Эффективность захоронения углекислого газа

Так как СО2 считается парниковым газом, то рассмотрим также альтернативный критерий оптимизации — максимальный объем закачанного СО2. Для оценки эффективности захоронения углекислого газа введем параметр, характеризующий отношение массы газа, находящейся в пласте, к массе, закачанной в пласт:

i ( q gi - q gp ) dt '

E = ⁰--> max .

t i qgpdt'

По аналогии с рисунком 5 построена карта оптимальных стратегий эффективности захоронения СО₂ при различных ценах нефти и скоростях закачки (Рис. 6 а ). Для сравнения обе карты наложим друг на друга (см. Рис. 6 б ). Таким образом, можно выделить области оптимальных стратегий для критериев (6) и (7) с их одновременным использованием при оценке стратегии. Так существуют области WG, согласующиеся с более высокими значениями чистой прибыли при 1( Ое [ 0;0,9 ] и 1( Ое [ 1;3 ] , и область GW, находящуюся в соответствии с более низкими значениями чистой прибыли при 1( О е [ 0,3; 1 ] .

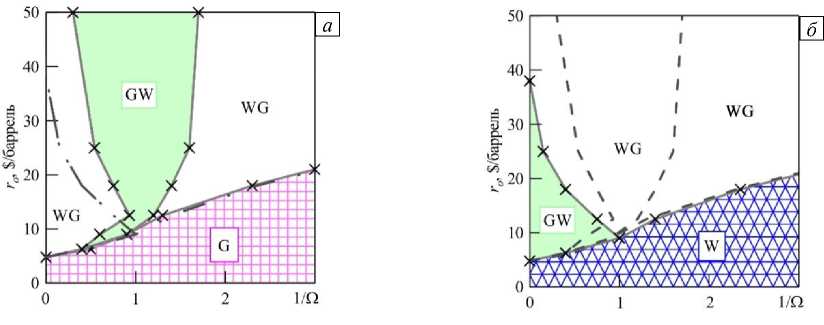
Рис. 6. Оптимальные стратегии при разных критериях оптимизации: ( а ) – (7), штрихпунктирные линии соответствуют критерию (6); (б) – (6), штриховые линии соответствуют критерию (7)

• 3.4.    Сравнение результатов расчетов на различных сетках

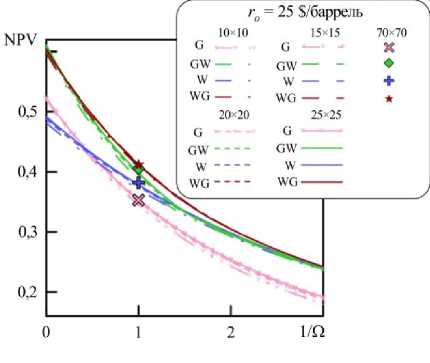
В данной работе рассмотрен резервуар размерами L х L Расчетная область равномерно разбивалась на 25×25 ячеек. Такая сетка выглядит достаточно грубой. Однако при переходе от 1-D к 2-D модели пласта существенно увеличивается трудоемкость оптимизационных вычислений (требуются множественные расчеты при различных параметрах нагнетания [15]). Для оценки погрешности вычислений использовались различные расчетные сетки. С этой целью апробированы четыре сетки с числом ячеек 10×10, 15×15, 20×20, 25×25, то есть количество ячеек от сетки к сетке увеличивалось на 125, 175 и 225, в связи с этим возрастало и время, затрачиваемое на моделирование фильтрации.

Оценим, насколько хорошо результаты вычислений соответствуют друг другу. Как видно из рисунка 7 а , линии, рассчитанные на сетке 10×10, лежат ниже графиков, отвечающих другим, более мелким, сеткам. Однако данные расчетов на всех сетках хорошо согласуются друг с другом, из чего можно сделать вывод, что измельчение сетки сказывается незначительно.

а

Рис. 7. Зависимости NPV, полученные с использованием разных сеток: от 1/ О ( a ); от числа ячеек при О = 1 ( б )

г = 25 $/баррель

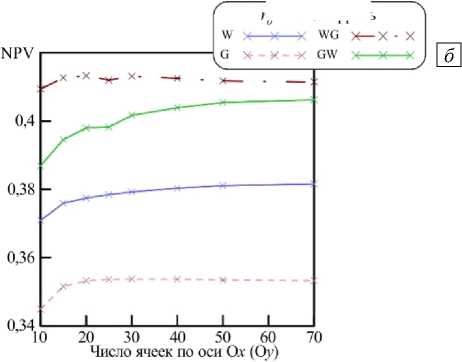
Рассмотрим, как зависит значение NPV в различных оптимизированных стратегиях при зафиксированной скорости закачки ( О = 1) от увеличения количества ячеек сетки (Рис. 7 б ). Значение NPV в стратегии GW растет при измельчении сетки от 10×10 до 30×30 ячеек. Однако в остальных стратегиях при сетках с большим, чем 20×20 числом ячеек, значения NPV изменяются мало. Результаты расчетов на сетке 70x70 при О = 1 также показаны на рисунке 7 а . Из рисунка видно что, рассчитанные на более мелкой сетке значения NPV для стратегий G и WG совпадают со значениями на сетке 25×25, а для стратегий W и GW они чуть больше. Следовательно, расчетная сетка 25×25 позволяет получать достаточно точные результаты.

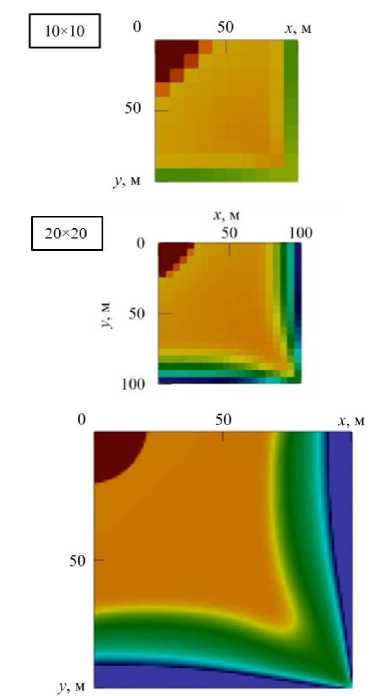
Рассмотрим, как выглядит фронт вытеснения на разных сетках при закачке CO 2 согласно стратегии G (Рис. 8). Вблизи нагнетательной скважины значения насыщенности газа ( s ) максимальны. Вдоль границ x = L и y = L насыщенность минимальна. Как видно на рисунке 8 б, на сетке 100x100, вдоль границ

а

б

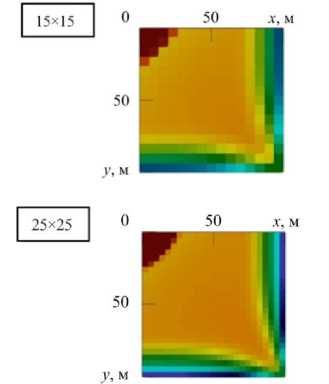
Рис. 8. Распределение насыщенности CO 2 при 1/ Q = 3 на расчетных сетках 10*10, 15x15, 20×20, 25×25 ( а ) и 100×100 ( б ) в момент его прорыва (PVI = 1,227) к добывающей скважине (стратегия G)

x = L и y = L насыщенность нулевая. Так как другие сетки имеют более крупные ячейки, то значения проницаемостей в этих ячейках осредняем. Как можно видеть, течение качественно не меняется при измельчении сетки, что подтверждает сеточную сходимость решения.

• 3.5.    WAG и SWAG стратегии водогазового воздействия

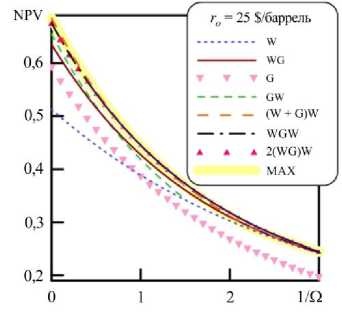
Введем новые обозначения: для одновременной закачки воды и газа — (W+G), и для n повторений последовательности WG (циклов WAG — Water–Alternating–Gas [19]) — n (WG). Так, аббревиатура (W+G)W обозначает стратегию, которая начинается с одновременной подачи в пласт двухфазной смеси воды и газа, и далее осуществляется переключение на закачку воды. Эта стратегия определяется тремя параметрами, а именно продолжительностью стадий (W+G) и W и объемной долей газа на первой стадии. Аббревиатура 2(WG)W обозначает стратегию, начинающуюся с двух одинаковых циклов WAG (вода закачивается первой, затем производится закачка газа), далее снова подается вода. Для этой стратегии также необходимо знать три параметра — продолжительности каждой независимой стадии.

Обратимся к рисунку 9. В области 1( Qe [ 0;0,4 ] , соответствующей быстрой закачке, можно видеть,

а

Рис. 9. WAG и SWAG стратегии закачки газа в 1-D ( a ) и 2-D ( б ) случаях

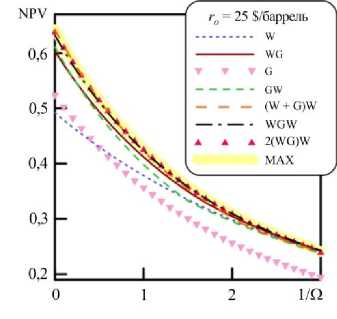
б

что более эффективной становится стратегия WGW. Аналогичная картина наблюдается при одномерной постановке задачи. Быстрой закачке 1J Qe [ 0;1 ] , отвечает оптимальная стратегия (W+G)W, а интервалу 1/ О е [ 1; 3] — стратегия 2(WG)W. Отметим, что результаты расчетов WAG и SWAG стратегий хорошо согласуются друг с другом как в 1-D, так и в 2-D случае. Из этого следует, что эти оптимальные стратегии водогазового воздействия в 1-D и 2-D случаях качественно совпадают.

4.    Заключение

Проведено сравнение решений одномерной и двумерной задач фильтрации с целью поиска оптимального водогазового воздействия на нефтяной пласт (то есть определения последовательности этапов закачки воды и/или газа). Показано, что:

• 1.    Поочередная закачка воды и газа позволяет получить большее значение NPV, чем закачка газа или воды по отдельности. Этот результат согласуется с работами [2, 19], где также продемонстрировано, что водогазовое воздействие экономически может быть более целесообразным методом увеличения нефтеотдачи. Однако, в настоящей работе и в [6] выявлено, что результат зависит от скорости нагнетания О . Так, при медленном темпе закачки и низких значениях цены нефти т_о оптимальной стратегией является W. При 2-D постановке задачи и r = 25 $/баррель оптимальной стратегией закачки при 1/0 е [ 0; 0,4 ] становится (W+G)W, то есть одновременная закачка воды и газа с последующей закачкой воды, далее, при 1( О е [ 0,4; 3] — WGW — последовательная закачка воды, газа и воды.

• 2.    Вычисленные области оптимальных стратегий закачки углекислого газа качественно совпадают друг с другом при 1-D и 2-D постановках задачи. Это дает возможность применения 1-D расчетов для определения оптимальных стратегий площадной закачки воды и газа.

• 3.  Значения NPV, соответствующие 2-D случаю, всегда ниже значений 1-D. Это происходит

• 4.  Существуют области оптимальных стратегий закачки, совпадающие при различных критериях

• 5.    Рассчитываемые параметры течения качественно не изменяются при использовании сеток с разной степенью дробления.

вследствие уменьшения объема пласта, охваченного вытеснением.

оптимизации.

Работа выполнена при финансовой поддержке РФФИ (проект № 20-31-80009).