Сравнение схем с расщеплением потока для численного решения уравнений Эйлера сжимаемого газа
Автор: Смирнова Н.С.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Математика
Статья в выпуске: 1 (37) т.10, 2018 года.
Бесплатный доступ
Статья посвящена сравнению схем с расщеплением потока для уравнений Эйлера сжимаемого газа. Рассматриваются четыре схемы с расщеплением потока: Steger- Warming, van Leer, AUSM+-up и Toro-V´azquez. Проводится серия вычислений на ряде одномерных тестов, а также задаче двойного Маховского отражения. Результаты рас- четов позволяют сделать вывод о преимуществе методов van Leer и AUSM+-up над другими подходами c расщеплением потока.
Уравнения эйлера, схемы с расщеплением потока, схема steger- warming, схема van leer, схема ausm+-up, схема toro-v´azquez, схема hllc, задача двойного маховского отражения
Короткий адрес: https://sciup.org/142215012
IDR: 142215012 | УДК: 519.63
Текст научной статьи Сравнение схем с расщеплением потока для численного решения уравнений Эйлера сжимаемого газа
В газовой динамике широко используется модель идеального газа. [1], движение которого описывается с помощью уравнений Эйлера. Для получения численного решения уравнений Эйлера, сжимаемого газа, рассматриваются противопоточные схемы. Дискретизация уравнений на. сетке осуществляется с учетом направления распространения возмущения, что позволяет учитывать физические свойства, течения. Существуют два. основных подхода, для выявления направления потока: методы типа. Годунова. [2], [3] и методы с расщеплением потока. [4].
Первый подход основывается на. модели, в которой поток на. границе между ячейками аппроксимируется с помощью точного или приближённого решения задачи о распаде произвольного разрыва. К схемам типа. Годунова, относятся HLL (Harten-Lax-van Leer) [5], HLLC (Harten-Lax-van Leer-Contact) [6] и др.
Во втором подходе для аппроксимации потока используется интерпретация, в которой взаимодействие между ячейками осуществляется через группы частиц, перемещающихся между ячейками и имеющих заданное распределение скоростей. Для разделения групп © Смирнова Н. С., 2018
«Московский физико-технический институт (государственный университет)», 2018
частиц на движущиеся «назад» и «вперед» применяют декомпозицию вектора невязкого потока на несколько частей. В настоящее время этот подход активно применяется в аэродинамике, так как имеет ряд преимуществ. Он достаточно быстро определяет направление распространения возмущения и имеет сравнительно простое расширение для расчетов реальных газов. Кроме этого, методы расщепления потока хорошо применимы для неявных схем, которые при решении задач аэродинамики являются предпочтительнее явных методов. Но уменьшенная сложность таких схем по сравнению со схемами типа Годунова приводит к ухудшению разрешения разрывов, в особенности контактных волн. К схемам с расщеплением потока относятся схемы: Steger-Warming [7], van Leer [8], AUSM+-up (Advection-Upstream-Splitting-Method) [9], Toro-Vazquez [10], [11] и др.
В данной работе проводится сравнение схем с расщеплением потока для уравнений Эйлера сжимаемого газа в приложении к течениям с большими числами Маха. В качестве основных критериев сравнения выступают надежность счета, точность разрешения контактных разрывов и отсутствие паразитных решений на ударной волне, таких как «карбункул».
Работа организована следующим образом: в и. 2 рассматриваются уравнения Эйлера и их дискретизация, в и. 3 описываются четыре схемы с расщеплением потока (Steger-Warming, van Leer, AUSM+-up, Toro-Vazquez), n. 4 посвящен результатам расчетов на ряде тестовых задач и сравнению данных схем.
-
2. Уравнения Эйлера
Рассмотрим гиперболическую систему уравнений газовой динамики в переменных Эйлера. Данная система выражает три основных закона сохранения — массы, импульса и энергии. В трехмерном случае система уравнений Эйлера сжимаемого газа в дивергентной форме выглядит следующим образом:
U + I- F + I- G + у H = 0 . (1) at ох оу OZ
Вектор U является вектором консервативных переменных, aF, G и H физические потоки в X, У и Z направлениях соответственно, которые представляют собой функции зависимости от консервативных переменных и задаются таким образом:
Е = р • (+ е), V2 = u2 + v2 + w2, где е — внутренняя энергия газа.
Для замыкания уравнений необходимо уравнение состояния газа, которое задает внутреннюю энергию. Для совершенного газа, уравнение состояния имеет следующий вид:
е(р-р) = рғЭ) - здесь у — показатель адиабаты.
Для дискретизации уравнений Эйлера сжимаемого газа используется метод конечных объемов [4]. Этот метод требует расчета численного потока по нормали к рассматриваемой ячейке, элемента расчетной сетки. В данной работе проводились вычисления на структурированной декартовой сетке, поэтому далее будем рассматривать лишь поток F в Х-направлении. Для трехмерной декартовой сетки конечно-объемная схема с потоком в Х-направлении записывается в виде консервативной схемы:
и Г+1
= U i
At
— Аж (Fi+ 2
-
F -- . >■
где численные потоки F +1, F —i через границы ячейки г могут быть найдены с помощью схем типа Годунова или схем с расщеплением потока.
В представленной работе были получены численные решения уравнений Эйлера в одномерной и двумерной постановке. Из трехмерного случая можно легко перейти к двумерному и одномерному: в первом случае приняв скорость w равной нулю, а во втором случае обнулив скорости г и w в векторе потока F.
-
3. Схемы с расщеплением потока
-
3.1. Метод Steger-Warming
В данном разделе рассмотрим четыре метода разбиения потока для расчета численных потоков в консервативной схеме (2): метод Steger-Warming [7], метод van Leer [8], метод AUSM+-up [9] и метод Toro-Vazquez [10], [11]. Описание первых двух схем также приведено в книге Е.Ф. Торо [4].
Метод Steger-Warming [7] был развит как обобщение противопоточных методов на дозвуковые области течений газа. Данная схема расщепления основана на декомпозиции вектора потока на два вектора F + и F -, у которых матрицы Якоби имеют неотрицательные и неположительные собственные значения соответственно.
Рассмотрим диагональную матрицу Л, составленную из собственных чисел Ai матрицы Якоби A = dU вектора потока. Можио представить матрицу Л в виде суммы матрицы Л +. у которой собственные числа А+ неотрицательные, и матрицы Л - с неположительными собственными числами А-:
Л = Л + + Л -.
Стегер и Уорминг предложили взять собственные числа А± равными
А± = 2(А ±|А|).
Матрицу A можно выразить через диагональную матрицу с помощью формулы
A = КЛК -1,
K — матрица из соответствующих собственных правых векторов. Далее, используя свойство однородности вектора потока, получаем расщепление газодинамического потока:
F = AU = КЛК -1 и = К ( Л + + Л -) К -1 и = ( A + + A -) U = F + + F -.
Собственные числа матрицы Якоби вектора потока в системе уравнений Эйлера (1) таковы:
А1 = и — а, А2 = Аз = А4 = и, А5 = и + а.
Составляющие газодинамического потока определяются следующим образом:
/ а ± +2(7 — 1)А± + А± \
F ± = f-
(и — а) А± + 2(7 — 1)иА± + (и + а) А± гА± + 2(7 — 1) г А± + гА± wA± + 2(7 — 1)wA± + wA±
\ (Н — иа)А± + (7 — 1)V2A± + (Н + иа)А± / где Н — энтальпия, определяемая следующим выражением:
Е + р п2 + V2 + w2 а2
Р 2 + 7 - 1"
Запишем численный поток через грань г + 2 для схемы (2), применив идею построения противопоточных схем:
гг+ 2 = f + ( ud + F-(ur+1). (3)
Численный поток Ғ^і на границе между двумя ячейками гиг + 1 интерпретируется как композиция компоненты потока Ғ+ . движущейся впер ед из левой ячейки г, и компоненты потока Ғ-1, идущей назад из правой ячейки г + 1.
При таком методе расщепления вектора потока при аппроксимации конвективных членов возникает диффузионный член первого порядка, что позволяет устойчиво рассчитывать скачки в течении газа, но использование данной схемы приводит к неблагоприятным результатам в звуковой точке.
-
3.2. Метод van Leer
Ван Лир [8] предложил сделать расщепление потока для уравнений Эйлера, как и в методе Steger-Warming, на два таких слагаемых, что матрица Якоби первого слагаемого обладает неотрицательными собственными числами, а матрица Якоби второго - неположительными собственными числами. Ван Лир сформулировал условия, которым должно удовлетворять данное расщепление:
-
1) Компоненты /+ и / потоков F± повторяют симметрию / относительно числа Маха, т.е / + (М ) = ±/ -(-М ). осли /(М) = ±/(-М).
2) Матрицы Якоби
а + = dF+
9 U ’
A -
d F-
dU
должны быть непрерывными.
ТТ А -I- А —
-
3) При дозвуковом течении расщепленные потоки вырождены, т.е А+ и A имеют ну
левое собственное число.
-
4) Потоки Ғ±должны быть непрерывны:
Ғ+ = Ғ если М > 1;
Ғ- = Ғ если М < 1.
-
5) Составляющие Ғ± — полиномы от числа Маха наименьшей степени.
Условия (1) и (2) были введены для устранения особенностей в звуковой точке и для получения более гладкого численного решения. Условие (4) гарантирует, что данное расщепление в сверхзвуковых областях сводится к стандартному противопоточному методу. Наконец, условие (5) позволяет однозначно найти расщепленние газодинамического потока.
Исходя из вышеизложенных требований, ван Лир построил расщепление для системы уравнений Эйлера (1):
Ғ± = ± 1 ра(1 ±М )2
'здесь число Наха, М = ^.
Как и в схеме Steger-Warming, расчет численного потока на границе осуществляется с помощью схемы (3).
Ван Лир оценивает устойчивость данной схемы с помощью неравенства
Сс, ,sА (М + „ ) 6 Д+ММ—л .
^ Аж 1 у ±3
Заметим, что Ссц = Ссц(М ). Возьмем показатель ;учиабаты для воздуха, у = 1.4:
cm x = 1 , | м । = 1 ,
С^ м 0 . 636 ..., |М| = 0 .
Таким образом, условие устойчивости в зависимости от числа Маха М может быть сильнее для данного метода, чем для схемы Годунова или Steger-Warming, у которых CCji 6 1. Следовательно, для получения устойчивого численного решения с помощью схемы van Leer будет требоваться больше времени.
3.3. Метод AUSM+-ир
Основная идея семейства схем AUSM (Advection-Upstream-Splitting-Method) заключается в представлении конвективной волны и акустической волны как два физически различных процесса. Невязкий поток в схеме AUSM+-пр [9] расщепляется на конвективный поток и поток с давлением:
F = FC ± P = mФ ± P, где m = ри, Ф = ( 1 и г w Н У, P = ( 0 р 0 0 0 )Т.
В зависимости от процесса, первое или второе слагаемое играет ключевую роль. Например, при нагреве стенки в пограничном слое поток массы оказывает большее влияние, а. поперек разрыва. - давление.
Конвективная часть представляет собой произведение скалярной величины-массы на. вектор Ф. Числовой поток на границе между двумя ячейками можно записать следующим образом:
m ± Im I , m — | m I F 2 = ф+ ± ф- ± p N
N = ( 0 пж ny пг 0 )Т.
Данный метод позволяет вычислять поток на границе между произвольно расположенными ячейками с введением внешней к границе ячейки г нормали n = ( пж, Пу , пг). В данной работе расчеты проводятся на. декартовой сетке, поэтому в этом случае вектор нормали на правой границе ячейки г задается как n = (1 , 0 , 0). Далее индексы l , r будут обозначать значения величин слева, и справа, от границы.
Поток массы
Поток массы через границу между ячейками рассчитывается по противопоточному правилу:
. \ PL, Мі/2 > 0, m = М1/2“1/2 1 PK, М1/2 < 0.
Число Маха. на. границе определяется как сумма, неотрицательной, неположительной и диффузионной составляющей:
М1/2 = М + ± М - ± Мр,
М + 11 М
выражаются аналогично формулам в методе van Leer с помощвю полиномиаль-
ной функции от величины М :
±_ Г 2(М ±|М|),
М =| ±4(М ± 1)2 ± 8(М2 - 1)2,
|М| > 1.
|М| < 1.
Vn
М = — о1/2
u·n
.
о1/2
Третье слагаемое Мр — это диффузионный член, который вводится для улучшения численных расчетов при низких и трансзвуковых значений числа Маха:
Мр =
-
К р max(1 - аМ2, 0) Та
-—_
PR
-
PL
POl/2 ’
М 2
мL + мR
2 ,
P L + PR
P 2
.
С помощью функции max диффузионный член исчезает при больших числах Маха и влияет на расчет числа Маха на границе при М 2< К Область значений чисел Маха, в которой этот член появляется, регулируется с помощью параметра а, который принимает положительные значения меньше единицы. Коэффициент Кр можно варьировать в промежутке от нуля до единицы. Функция /а определяется таким образом:
/а(Мо) = Мо(2 - Мо),
где
М2 = min(1, max(М 2,МС0).
Мсо — «cut-off» параметр, обычно берется такого же порядка, как число Маха на бесконечности М^ (в невозмущенном пространстве). Мсо не должно обращаться в ноль, иначе это будет приводить к численной ошибке.
Скорость звука на границе между ячейками выражается так:
01/2 = min(oL,OR), _ о*2 _ о*2
L max(o*,V+) , R max(o*,-V„7)1
здесь о* — критическая скорость звука, полученная из условия, что локальное значение числа Маха равняется единице:
о*2
2(7 - 1)„ ---------и .
7 + 1
Потоковая часть с давлением
Вектор давления зависит только от между ячейками следующим образом:
давления, которое аппроксимируется на границе
P = Р +|а • PL + Р |а • PR + Pu,
здесь Р ± — полином пятой степени от числа Маха:
Р ± = / 2(1 ± 8І9п(М)),
[ 4(М ± 1)2(2 щ М ) ± аМ(М 2
- 1)2 ,
|М| > 1.
|М| < 1.
а = Т7(-4 + 5Та ) е [
А]
4’ 16]
Как и для потока массы, здесь вводится диффузионный член pu:
Pu = -Ku •Р + •Р • (PL + PR) • (Тааі/2) • (V~ - VT+).
Во всех нижепредставленных вычислениях параметры в схеме AUSM+-ир полагались равными следующим величинам:
а = 1, Мсо = М^, Кр = 0.25, Ku = 0.75.
-
3.4. Метод Toro-Vazquez
Торо и Васкес-Сендон [10], [11] предложили метод расщепления, в котором поток F ( U ) представляется в виде суммы конвективной части A ( U ) и части с давлением P ( U ):
/ pm \ ри2 + р
F(U) = puv I = A(U) + P(U), puw
\u( 2 pV 2 + pe + р))
где A(U) 11 P(U) задаются столбцами:
A(U) = и
( P pu pv
— u K ( U ) ,
P(U) =
pw
\ 2 pVP
/ 0
р
\ u(pe + р)/
Обратим внимание, что конвективная часть не содержит переменной давления. Все переменные р входят во вторую потоковую часть.
Система уравнений Эйлера разбивается на две системы:
U + dL A = 0 at ох
и
It и + Г p = о - at ох
Рассмотрим последовательно систему с потоковой частью P(U) и систему с потоковой частью A ( U ).
Система с потоковой частью P(U)
Запишем данную систему в терминах физических переменных где
|
p^ |
0 |
0 |
|
и |
0 |
0 |
|
V — v , B — |
0 |
0 |
|
w |
0 |
0 |
|
\ р) |
0 |
др |
0 0 0
0 0 р
0 0 0
0 0 0
0 0 и)
Собственные числа матрицы B
Ai — 2 (u - А)< А2 — A3 — А4 —
0 <Х5
= |( и + А ) ,
где
А — -
Заметим, что данная система является гиперболической, так как все собственные числа вещественны, а соответствующие им правые собственные векторы линейно независимы. Так как и всегда меньше А, то поток в этой системе дозвуковой. Это значит, что в исходной системе Эйлера трансзвуковые области течений газа не требуют введения дополнительных поправок во избежание возникновения особенностей в звуковой точке.
Далее рассмотрим локальную задачу Римана:
Д V + B(V) 7 V = 0, at ' / ox , x < 0, x > 0.
( ү, = ү и
v ( - 0) ={ v R ; v+ „
Собственным числам A2,3,4 соответствует контактный разрыв, сопровождающийся скачком плотности со значения p l на pr. Слева и справа от контактной волны идут «нелинейные» волны. Будем искать п* и р* в области между левой и правой волнами. Решение получим путем аппроксимации с помощью инвариантов Римана:
п."+ 2
Р*+ 2
C r u r - C l u l C r - C l
C r P l - C l P r C r - C l
- c r - c l (p r - PL),
+ 2 C r — C l ( h r - nL ) ,
где
C l = P l (u l - AL), O r = p r (u r + Ar).
Этот способ плохо реализуется при наличии сильных ударных волн для задачи Римана в консервативных переменных U = (р, рп, pv, pw,E)T.
Теперь можно найти численный поток давления
|
0 р*+ 2 |
|
|
P .+2 = |
0 0 1 А п*+ 2 р*+ 2 у |
Конвективная система
Легко показать, что конвективная система является слабогиперболической, так как собственным числам соответствует неполный набор линейно независимых правых векторов. Конвективную часть запишем следующим образом:
A ( U ) =
|
/ рп \ |
/ Р |
|
рп2 |
рп |
|
рпv = п К ( и ) , |
K ( U ) = pv |
|
рпw |
pw |
|
\ 2РпУ 2/ |
\ 2pV 7 |
, что можно интерпретировать как перенос вектора K (массы, импульса, кинетической энергии) со скоростью п. Для построения численных потоков конвективной системы Торо и Васкес-Сендон предложили 2 алгоритма.
Схема ТУ
Схема основана на представлении конвективного потока:
A(U) =п*+1K, где п*+ 1 — конвективная скорость между узлами гиг + 1, которая находится из задачи Римана для системы с потоком P(U). Численный поток рассчитывается по противопоточ- ному правилу:
A + 2 = п*+ 2
K V,
и кг+1,
если п* ! > 0. г+ 2
если п* ! 6 0. г+ 2
Схема TV-AWS
Торо и Васкес-Сендон представили модификацию схемы, предложенной в методе Zha-Bilgen [12] для конвективной системы.
A+ 2 = A+ + A-+1, где
A- = 2(1 — »№*, а+ = 2(1 + сиНК, ш = ЦиГ) =
Уё+Т^Т,
е - малая положительная величина, например, е = 0.1.
Численное решение уравнений Эйлера с помощью метода Toro-Vazquez можно найти, используя консервативную схему (2), где численный газодинамический поток равен следующей сумме:
F i+2 = A i+ 2 + P i+2.
В работе конвективный поток рассчитывался с помощью схемы TV.
-
4. Результаты расчетов
-
4.1. Одномерные задачи
В данном разделе представлены численные решения одномерных и двумерных уравнений Эйлера для сжимаемого газа на примере двух одномерных тестов и задачи двойного маховского отражения.
Для повышения порядка точности результатов в двумерном случае применялась конечно-объемная схема WENO (Weighted Essentially Non-Oscillatory) [13], [14]. Обозначим схемы с потоком X как WENO-Х. Тогда, например, схема с потоком, вычисляемым с помощью метода HLLC, будет обозначаться как WENO-HLLC.
Схемы WENO-Х используют выпуклую линейную комбинацию шаблонов из трех точек с адаптивными коэффициентами для блока реконструкции. Адаптивный шаблон строится таким образом, чтобы он не пересекал разрыв, иначе возникает эффект Гиббса, т.е. если какой-то шаблон содержит разрыв, то соответствующий весовой коэффициент должен быть близким к нулю. Данная схема WENO-Х имеет 5-й порядок по пространству и 3-й по времени.
В представленной работе были получены численные решения одномерных уравнений Эйлера с помощью четырех схем с расщеплением потока: Steger-Warming, van Leer, AUSM+-up и Toro-Vazquez. Расчеты данных методов сравниваются с точным решением на примере двух тестовых задач, постановка которых взята из книги Е.Ф. Торо [4].
В качестве начальных данных рассматриваются две области с газом, разделенные перегородкой жд. Слева и справа от мембраны в момент времени t = 0 задаются векторы начальных значений физических переменных V l = (p l ,u l ,Pl)T и V r = (p r ,u r ,P r )T• В следующий момент времени перегородка жд убирается, и решается задача о распаде разрыва (задача Римана). В зависимости от тестовой задачи с течением времени формируются различные конфигурации разрывов.
Численные и точные решения были найдены в области 0 < ж < 1 . Проводилось сравнение полученных результатов при разбиении отрезка [0;1] на М = 100 и М = 1000 ячеек. Число Куранта было взято равным 0.9 (C cfl = 0.9) для всех методов, кроме van Leer, для него C cfl = 0.6. Начальные значения физических величин в тестовых задачах приведены в табл. 1.
Таблица!
Начальные данные для тестовых задач
|
Тест |
PL |
RL |
PL |
PR |
RR |
PR |
|
1 |
1.0 |
0.75 |
1.0 |
0.125 |
0.0 |
0.1 |
|
2 |
5.99924 |
19.5975 |
460.894 |
5.99242 |
-6.19633 |
46.0950 |
Тест 1
Тест 1 является модификацией задачи Сода при добавлении начальной скорости газа, помещенного слева от перегородки tq. Этот тест позволяет выявить, может ли численный метод допустить нарушение энтропийного условия. Решение данной задачи состоит из волны разрежения, контактной волны и правой ударной волны.
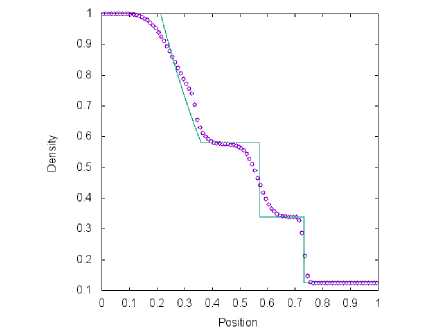
а) Сетка содержит М = 100 ячеек
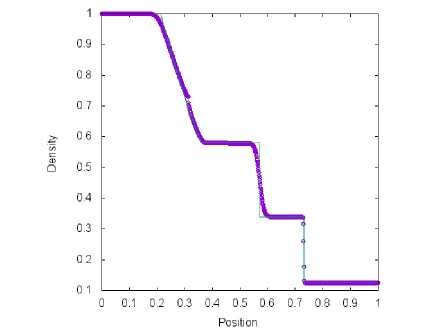
б) Сетка содержит М = 1000 ячеек
Рис. 1. Решение тестовой задачи 1 с помощью метода. Steger-Warming (символ) и точного решения (линия) в момент времени t = 0.2 пр и жо = 0.3
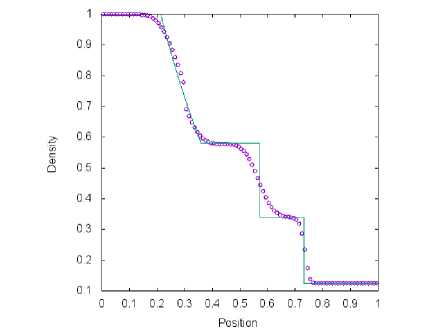
а) Сетка содержит М = 100 ячеек
Рис. 2. Решение тестовой задачи 1 с помощью метода, van Leer (символ) и точного решения (линия) в момент времени t = 0.2 пр и жо = 0.3
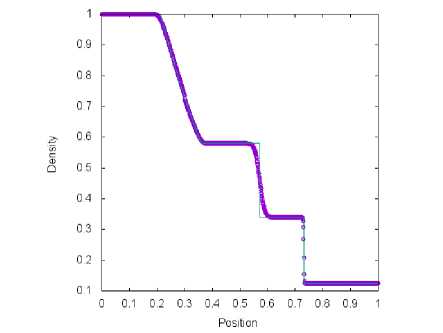
б) Сетка содержит М = 1000 ячеек
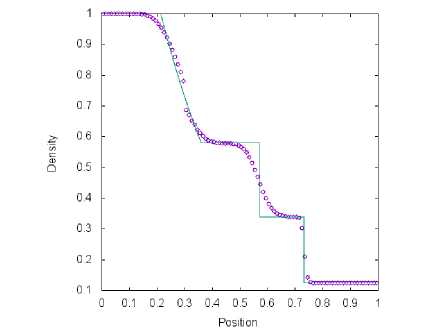
а) Сетка содержит М = 100 ячеек
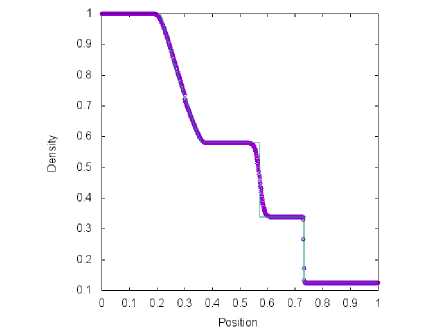
б) Сетка содержит М = 1000 ячеек
Рис. 3. Решение тестовой задачи 1 с помощью метода AUSM+-ир (символ) и точного решения (линия) в момент времени t = 0.2 пр и t q = 0.3
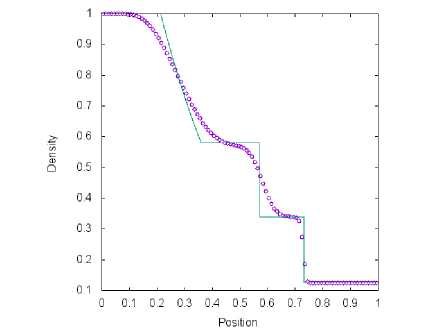
а) Сетка содержит М = 100 ячеек
Рис. 4. Решение тестовой задачи 1 с помощью метода. Toro-Vazquez (символ) и точного решения (линия) в момент времени t = 0.2 пр и t q = 0.3
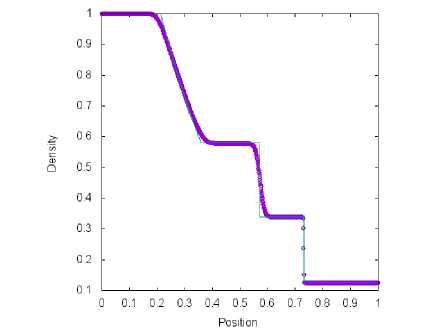
б) Сетка содержит М = 1000 ячеек
На рис. 1, 2, 3 и 4 представлены результаты решения тестовой задачи 1 для четырех схем. На рисунках проиллюстрирована зависимость плотности газа от координаты пространственной оси. Все схемы обеспечивают хорошее разрешение ударной волны и хуже справляются с контактной волной. На рис. 1, 2 и 3 возникает провал в разреженной волне в связи с невыполнением энтропийного неравенства в звуковой точке. Схема. TV (рис. 4) позволяет избежать этой ошибки. При увеличении числа, ячеек на. координатной оси можно увидеть на. графиках быструю сходимость численных результатов, полученных с помощью четырех методов, к точному решению.
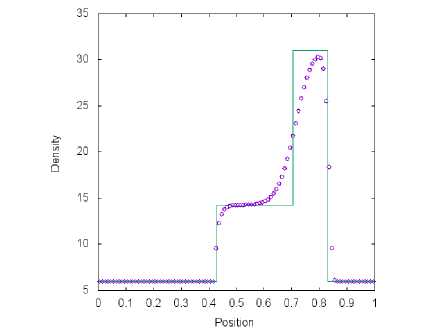
Тест 2
Тест 2 используется для проверки точности и устойчивости численного решения. В результате распада, разрыва, данной задачи возникают две ударные волны с контактной волной между ними.
а) Сетка содержит М = 100 ячеек
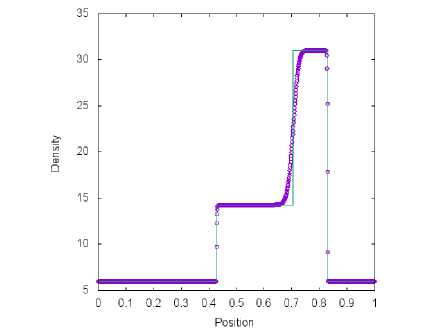
б) Сетка содержит М = 1000 ячеек
Рис. 5. Решение тестовой задачи 2 с помощью метода. Steger-Warming (символ) и точного решения (линия) в момент времени t = 0.035 пр и t q = 0.4
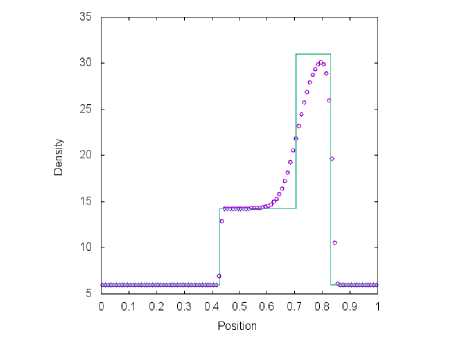
а) Сетка содержит М = 100 ячеек
Рис. 6. Решение тестовой задачи 2 с помощью метода, van Leer (символ) и точного решения (линия) в момент времени t = 0.035 пр и t q = 0.4
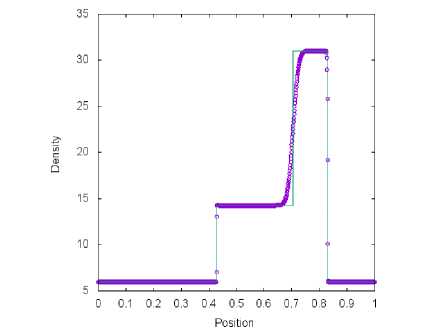
б) Сетка содержит М = 1000 ячеек
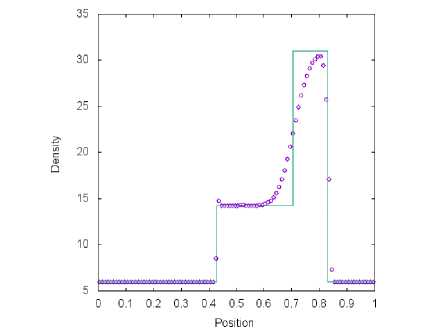
а) Сетка содержит М = 100 ячеек
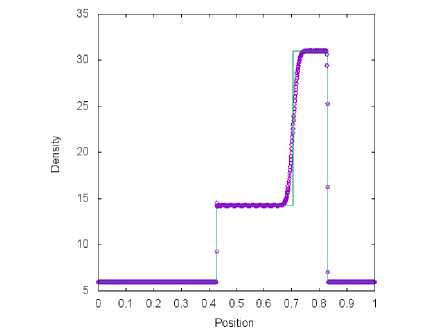
б) Сетка содержит М = 1000 ячеек
Рис. 7. Решение тестовой задачи 2 с помощью метода AUSM+-нр (символ) и точного решения (линия) в момент времени t = 0.035 пр и t q = 0.4
-
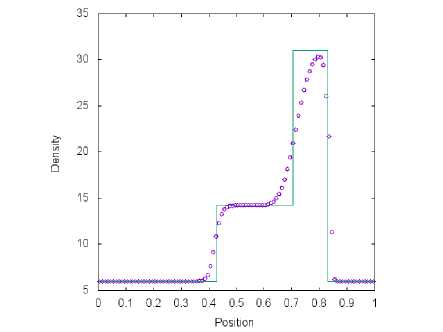
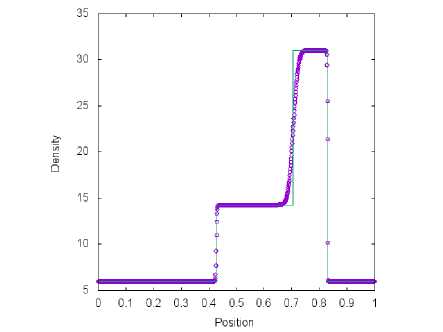
а) Сетка содержит М = 100 ячеек б) Сетка содержит М = 1000 ячеек
-
4.2. Задача двойного маховского отражения
Рис. 8. Решение тестовой задачи 2 с помощью метода. Toro-Vazquez (символ) и точного решения (линия) в момент времени t = 0.035 пр и х0 = 0.4
Результаты расчетов четырех схем, представленные на рис. 5, б, 7 и 8, сравниваются с точным решением. На полученных графиках зависимости плотности газа, от координаты сильная правая ударная волна хорошо прорабатывается во всех методах. Левая ударная волна лучше разрешена для схем van Leer (рис. 6) и AUSM+-пр (рис. 7) в сравнении с методами Toro-Vazquez (рис. 8) и Steger-Warming (рис. 5). Данные алгоритмы плохо выделяют контактные волны при заданном разбиении [0;1] на М = 100 ячеек. При уменьшении шага по координатной оси X численные результаты, полученные с помощью четырех способов расщепления потока, сходятся к точному решению.
Задача двойного маховского отражения [14], [15] тестирует численные схемы на способность обнаружить и разрешить неустойчивые контактные разрывы, а. также на. склонность к проявлению эффекта, «карбункула». Задача, не имеет точного аналитического решения, лишь экспериментальные подтверждения возникновения сложной ударно-волновой структуры [16].
В данной работе задача, формулируется следующим образом. Вычислительная область представляет собой прямоугольник размерами [0; 4] х [0; 1]. В начальный момент времени t = 0 сильная ударная волна с числом Маха М = 10 движется направо под углом 60° к горизонтальной оси X из положения х = j. Перед ударным фронтом давление и плотность газа задаются равными: р = 1 и р = 1.4. Расчет ведется с числом Куранта CFL = 0.45.
Программа, получающая численное решение задачи двойного маховского отражения, взята, из статьи [14]. Программа, была, модифицирована, добавлением численных расчетов потоков van Loor. WENO-AUSM+-up и WEXO-TV.
На рис. 9-20 представлены результаты, полученные с помощью методов WENO-HLLC, WENO-VanLeer, WENO-AUSM+-up и WENO-TV в момент времени t = 0.2. Расчеты были произведены на последовательности сеток с размерами 1920 х 480, 3840 х 960 и 5760 х 1440. Схема. Steger-Warming здесь не рассматривалась, так как в одномерном случае она. показала, результаты на. тестовых задачах хуже остальных.
При данном нерегулярном взаимодействии ударной волны с поверхностью возникают два. маховских отражения. Первое сопровождается появлением тройной точки, из которой исходит ударная отраженная волна, ножка. Маха, и контактный разрыв между ними. По мере удаления от тройной точки контактный разрыв теряет устойчивость. Второй контактный разрыв можно заметить вблизи нижней границы расчетной области. Взаимодействуя друг с другом, контактные разрывы образуют характерную связку, завихрения. В свою очередь, в отраженной волне появляется вторая тройная точка с дополнительным скач- ком уплотнения, который становится слабее и исчезает при приближении к контактному разрыву.
Наибольшую трудность у численного метода вызывает точность разрешения треугольной области с контактными разрывами. Схемы WENO-HLLC, WENO-VanLeer, WENO-AUSM +-up и WENO-TV дают схожие результаты на сетке 1920x480 (рис. 9-12). Сравнивая полученные результаты на более подробной сетке 3840 x 960, можно отметить, что схема WENO-HLLC (рис. 13) наиболее точно прорабатывает контактные разрывы, а схема WENO-TV (рис. 16) не справляется с неустойчивостью. При дальнейшем измельчении сетки схемы WENO-VanLeer (рис. 18) и WENO-AUSM+-пр (рис. 19) лучше разрешают треугольную область, чем WENO-HLLC (рис. 17) и WENO-TV (рис. 20).
Данная задача в связи с наличием сильных ударных волн вызывает проявление в схемах «карбункул»-неустойчивости. При решении теста на сетке 3840 x 960 методом WENO-TV (рис. 16) в ножке Маха явно виден нефизический излом, который и является проявлением эффекта «карбункула», что приводит к значительному искажению течения. При использовании схемы WENO-HLLC (рис. 13) не возникает ярко выраженного эфекта «карбункула», но наблюдается изгиб в ножке Маха. Схемы WENO-VanLeer (рис. 14) и WENO-AUSM+-up (рис. 15) более устойчивы к данному эффекту. На подробной сетке 5 760 x 1440 схема WENO-HLLC (рис. 17) дает значительный изгиб ножки Маха, который ухудшает разрешение треугольной области с контактными разрывами. Схема WENO-AUSM+-up (рис. 19) начинает проявлять склонность к «карбункулу».
Стоит подчеркнуть, что контактные разрывы - физические неустойчивые структуры. В реальности такие завихрения возникают из-за наличия в среде вязкости и теплопроводности, т.е такие структуры можно получить при численном решении уравнений Навье-Стокса. К уравнениям Эйлера, обладающим нулевой физической вязкостью, можно перейти при устремлении числа Рейнольдса к бесконечности в уравнениях Навье-Стокса. При численном решении уравнений Эйлера в качестве вязкости выступает схемная вязкость. Методы расчета уравнений Навье-Стокса также обладают схемной вязкостью, но при малых числах Рейнольдса физическая вязкость подавляет схемную. При увеличении же числа Рейнольдса схемная вязкость начинает играть большую роль. Задача двойного маховсокого отражения позволяет оценить схемную вязкость. Методы с большой схемной вязкостью проявляют сильные диссипативные свойства и размывают неустойчивые структуры. На основе представленных результатов можно заключить, что подход WENO-HLLC обладает меньшей схемной вязкостью, чем методы WENO-VanLeer, WENO-AUSM+-up и WENO-TV.
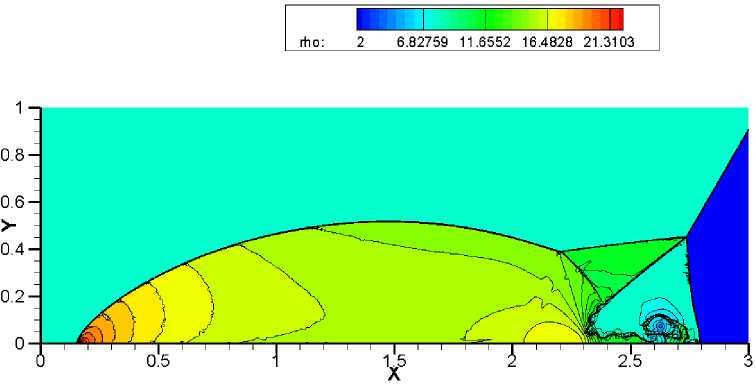
Рис. 9. Решение задачи двойного маховского отражения с помощью метода. WENO-HLLC. Сетка 1920 x 480. 30 контуров в диапазоне от 2 до 22
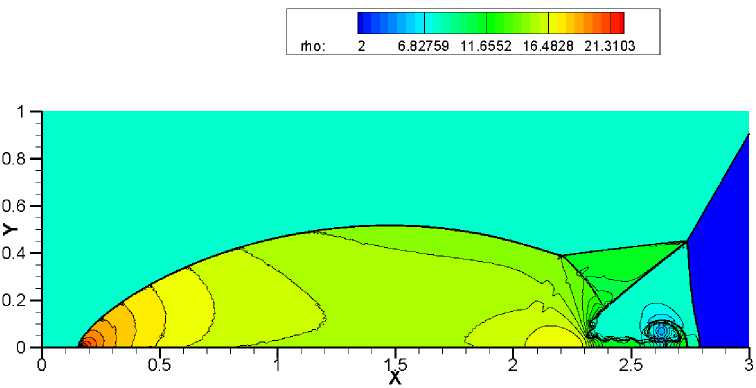
Рис. 10. Решение задачи двойного маховского отражения с помощью метода. WENO-VanLeer. Сетка 1920 х 480. 30 контуров в диапазоне от 2 до 22
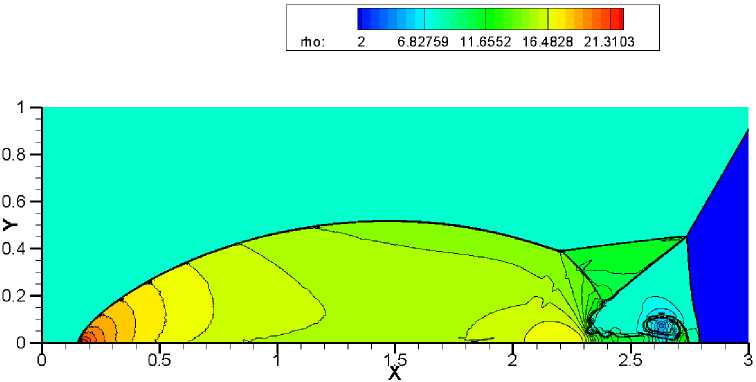
Рис. 11. Решение задачи двойного маховского отражения с помощью метода WENO-AUSM+-нр. Сетка 1920 х 480. 30 контуров в диапазоне от 2 до 22
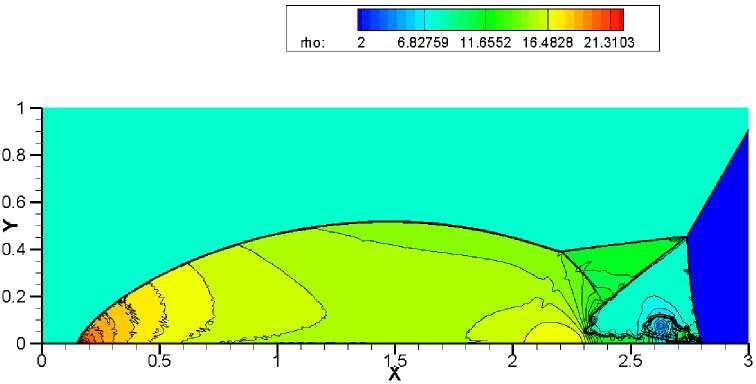
Рис. 12. Решение задачи двойного маховского отражения с помощью метода. WENO-TV. Сетка 1920 х 480. 30 контуров в диапазоне от 2 до 22
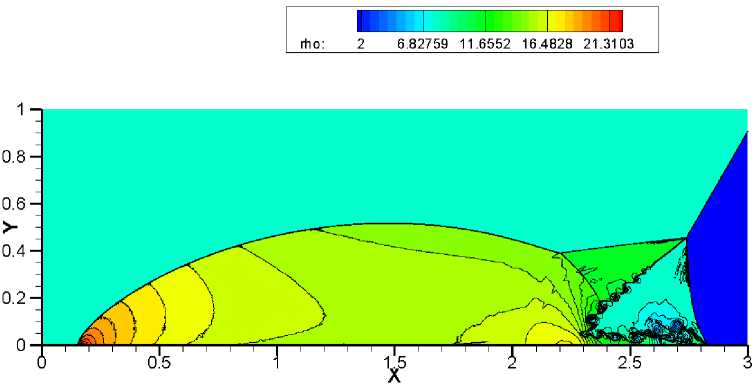
Рис. 13. Решение задачи двойного маховского отражения с помощью метода. WENO-HLLC. Сетка 3840 х 960. 30 контуров в диапазоне от 2 до 22
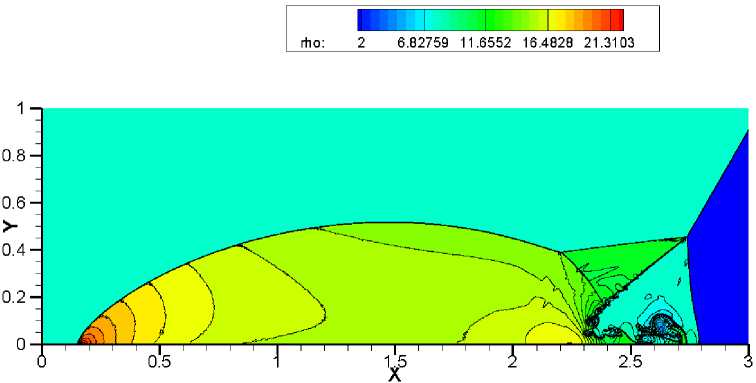
Рис. 14. Решение задачи двойного маховского отражения с помощью метода. WENO-VanLeer. Сетка 3840 х 960. 30 контуров в диапазоне от 2 до 22
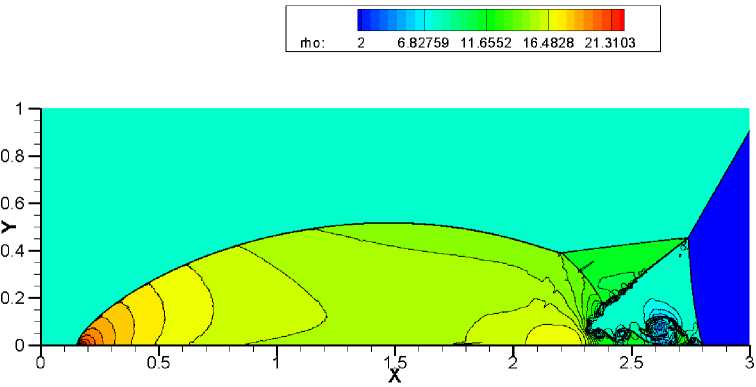
Рис. 15. Решение задачи двойного маховского отражения с помощью метода WENO-AUSM+-нр. Сетка 3840 х 960. 30 контуров в диапазоне от 2 до 22
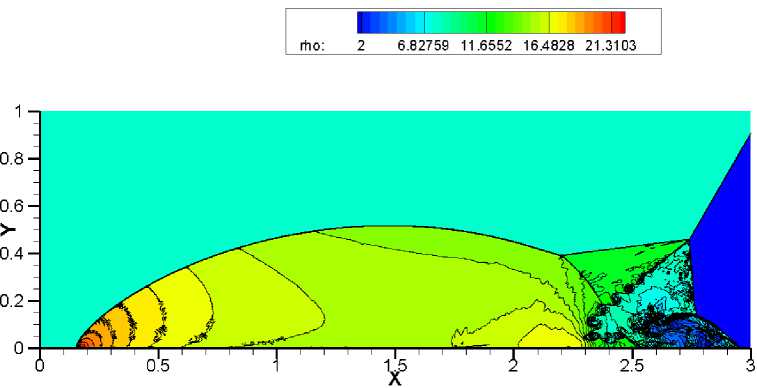
Рис. 16. Решение задачи двойного маховского отражения с помощью метода. WENO-TV. Сетка 3840 х 960. 30 контуров в диапазоне от 2 до 22
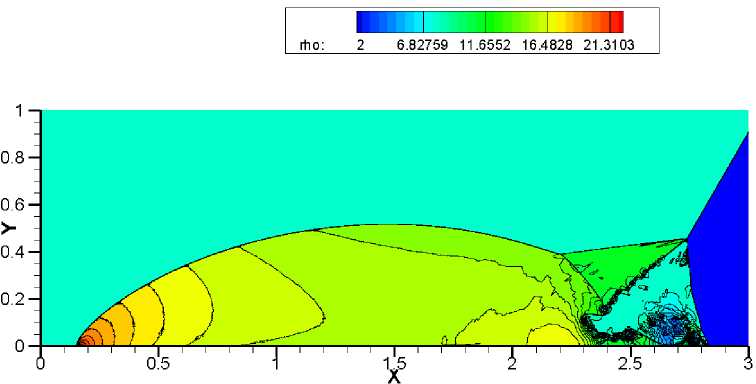
Рис. 17. Решение задачи двойного маховского отражения с помощью метода. WENO-HLLC. Сетка 5760 х 1440. 30 контуров в диапазоне от 2 до 22
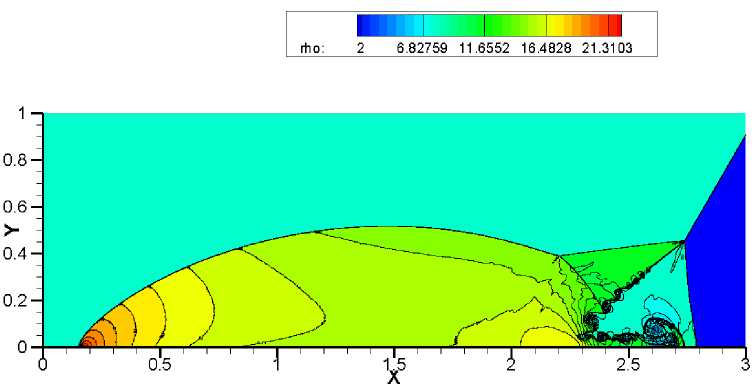
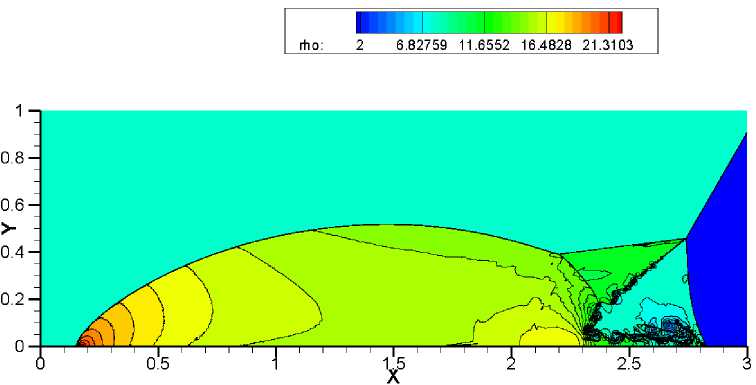
Рис. 19. Решение задачи двойного маховского отражения с помощью метода WENO-AUSM+-ир. Сетка 5760 х 1440. 30 контуров в диапазоне от 2 до 22
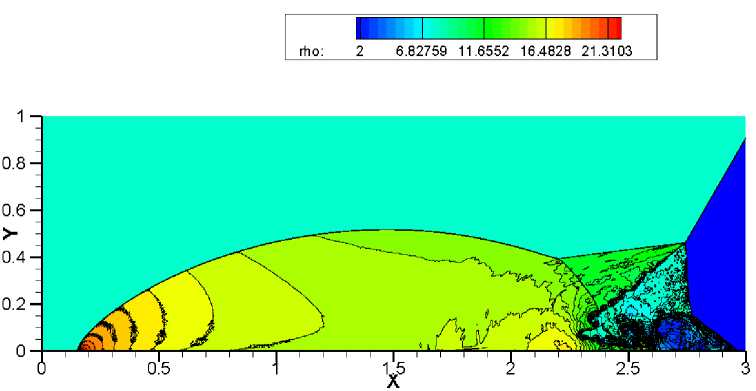
Рис. 20. Решение задачи двойного маховского отражения с помощью метода. WENO-TV. Сетка 5760 х 1440. 30 контуров в диапазоне от 2 до 22
-
5. Заключение
В настоящее время схемы с расщеплением потока, активно используются в аэродинамике. В данной работе проведено сравнение схем с расщеплением потока, разработанных в последнее время: Steger-Warming,van Leer, AUSM+-up, Toro-Vazquez, и хорошо себя зарекомендовавшей схемы типа. Годунова. HLLC, чтобы выявить наиболее эффективный метод расчета. Были получены численные решения уравнений Эйлера, для сжимаемого газа. на. примере одномерных тестов и задачи двойного маховского отражения.
Расчетные исследования позволили сделать следующие выводы. Схема. Steger-Warming наименее предпочтительна, для использования в задачах газовой динамики. Метод Toro-Vazquez хорошо применим в одномерных задачах, но проявляет «карбункул»-неустойчивость и не разрешает неустойчивые структуры в задаче двойного маховского отражения. В двумерной задаче схема HLLC показывает хорошее разрешение контактных разрывов, но имеет тенденцию к образованию «карбункула». Схемы van Leer и AUSM+-up дают лучшие результаты при моделировании сильных ударных структур.
Список литературы Сравнение схем с расщеплением потока для численного решения уравнений Эйлера сжимаемого газа
- Эглит М.Э. Лекции по основам механики сплошных сред. М.: Книжный дом «ЛИБРОКОМ», 2010.
- Годунов С.К. Разностный метод численного расчета разрывных решений уравнений гидродинамики//Математический сборник. 1959. T. 47, №3. C. 271-306.
- Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений. М.: Физматлит, 2001.
- Toro E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics. Springer, 2009.
- Harten A., Lax P.D., van Leer B. On upstream differencing and Godunov-type schemes for hyperbolic conservation laws//SIAM Review. 1983. V. 25, N 1. P. 35-61.
- Toro E.F., Spruce M., Speares W. Restoration of the Contact Surface in the Harten-Lax-van Leer Riemann Solver//Journal of Shock Waves. 1994. V. 4, N 1. P. 25-34.
- Steger J.L., Warming R.F. Flux Vector Splitting of the Inviscid Gasdynamic Equations with Applications to Finite Difference Methods//Journal of computational physics. 1981. V. 40, N 2. P. 263-293.
- Van Leer B. Flux-Vector Splitting for the Euler Equations//Eighth international conference on numerical methods in fluid dynamics. 1982. P. 507-512.
- Liou M.-S. A sequel to AUSM, Part II: AUSM+-up for all speeds//Journal of Computational Physics. 2006. V. 214, N 1. P. 137-170.
- Toro E.F., V´azquez-Cend´on M.E. Flux splitting schemes for the Euler equations//Computers and Fluids. 2012. V. 70. P. 1-12.
- Toro E.F., Castro C.A., Lee B.J. A novel numerical flux for the 3D Euler equations with general equation of state//Journal of Computational Physics. 2015. V. 303. P. 80-94.
- Zha G.-C., Bilgen E. Numerical solutions of Euler equations by using a new flux vector splitting scheme.//International Journal for Numerical Methods in Fluids. 1993. V. 17, N 2. P. 115-144.
- Jiang G.S., Shu C.W. Efficient implementation of weighted ENO schemes//Journal of Computational Physics. 1996. V. 126, N 1. P. 202-228.
- Titarev V.A., Toro E.F. Finite-volume WENO schemes for three-dimensional conservation laws//Journal of Computational Physics. 2004. V. 201, N 1. P. 238-260.
- Woodward P.R., Colella P. The numerical simulation of two-dimensional fluid flow with strong shocks//Journal of Computational Physics. 1984. V. 54, N 1. P. 115-173.
- Семенов А.Н., Березкина М.К., Красовская И.В. Классификация разновидностей отражения ударной волны от клина. Часть 2. Экспериментальное и численное исследование разновидностей маховского отражения//Журнал технической физики. 2009. T. 79, №4. C. 52-58.


