Сравнение скорости обработки транзакций в распределенных системах на основе распределенного реестра и направленного ациклического графа

В настоящее время наблюдается повышенный интерес к технологии распределенных реестров. Предполагается, что данная технология позволяет устранить ряд ограничений, присущих применяемым сегодня методам хранения данных, например, проблемы безопасности хранения и передачи данных и масштабируемости систем.

Технология распределенных реестров – это подход к обмену и хранению информации, при котором [1; 2]:

• •    каждый участник может обладать полноценной копией хранимых данных;

• •    синхронизация копий реестра происходит на основе протокола достижения распределенного консенсуса, то есть соглашения среди участников на добавление новой информации;

• •    каждый участник взаимодействия может иметь доступ к истории транзакций.

В классической технологии построения распределенного реестра у пользователей нет прямого доступа к самому реестру. Когда пользователь хочет добавить транзакцию в реестр, ему приходится отдавать поручение производителю верифицированных записей реестра (записи назовем блоками, а производителей – блок-продюсерами или майнерами). Майнеры решают, какую транзакцию добавить в следующий блок. У них есть эксклюзивный доступ к блокам и право решать, чью транзакцию принять для добавления в реестр с учетом применяемого алгоритма консенсуса. Таким образом, майнеры являются посредниками между пользователями и распределенным реестром. Но также майнеры являются гарантом роста сети и поддержания безопасности за счет внутренних механизмов взаимодействия узлов распределенных реестров.

Котилевец Игорь Денисович старший преподаватель кафедры цифровых технологиий обработки данных, МИРЭА – Российский технологический университет, Москва. Сфера научных интересов: базы данных, теория графов, системы массового обслуживания, технология распределенных реестров, интернет вещей. Автор более 50 опубликованных научных работ.

Однако данная технология имеет ограничение, которое замедляет ее внедрение в различные сферы жизни, например промышленность. Классический распределенный реестр не решает проблему масштабируемости, так как происходит снижение пропускной способности и скорости транзакций при существенном росте объемов транзакций из-за необходимости добавления транзакций в единую цепочку блоков и невозможности разделить процесс обработки в несколько потоков [3–5].

Для решения данной проблемы необходимо изменить архитектуру классического реестра и отказаться от логики блоков и блок-продюсеров. Для выстраивания цепочки блоков необходимо соединение самих транзакций путем включения в каждую транзакцию хешей нескольких предыдущих транзакций. В результате получается структура, известная в математике как направленный ациклический граф (Directed Acyclic Graph – DAG).

В данной работе приводится сравнительный анализ параметров математических моделей классического распределенного реестра и системы на основе направленного ациклического графа.

Модель распределенного реестра

В качестве параметров сравнения классического распределенного реестра и системы на основе направленного ациклического графа выбраны: время обработки одной транзакции, пропускная способность, количество устройств в сети, загруженность системы. Данные параметры необходимо рассчитать на основе входных параметров: количество устройств в сети, интенсивность поступления транзакций, время обработки транзакции одним устройством. Для расчета распределенной сети, построенной на основе классического распределенного реестра, можно представить систему обработки транзакции и создания нового блока как систему массового обслуживания. Системы массового обслуживания (далее – СМО) – это системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания. Данную математическую модель можно использовать в моделировании системы распределенных реестров, так как в качестве заявок могут выступать транзакции, а в качестве системы каналов обслуживания – устройства обрабатывающие транзакции. Рассмотрим классический распределенный реестр как одноканальную СМО с неограниченной очередью. Пусть все устройства в сети имеют одинаковую скорость обработки транзакции µ (пропускную способность):

Сравнение скорости обработки транзакций в распределенных системах ...

Ц=—, to6

где t _o6 - время обработки транзакции.

Данный параметр зависит от множества факторов: мощность устройства, загруженность устройства другими процессами, пропускная способность канала передачи, ско- рость передачи по каналу связи и др.

Новые транзакции поступают в систему с интервалом по заданному закону распределения с математическим ожиданием M ( x ) . Тогда интенсивность поступления заявок X = M ( x ) .

СМО с неограниченной очередью может находиться в бесконечном числе состояний. На Рисунке 1 представлен граф состояний системы обработки транзакций ( S ₀ – система свободна; S ₁ – система занята, обрабатывается транзакция, транзакций в очереди нет; S ₂ – система занята обработкой транзакции, в очереди на обработку 1-я транзакция; S ₃ – система занята обработкой транзакции, в очереди на обработку 2-я транзакция, и др.) [6].

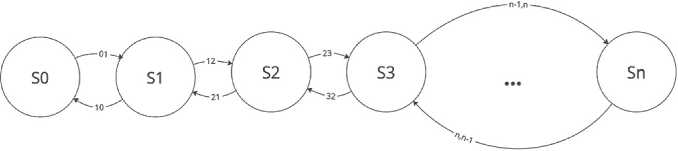
Рисунок 1. Граф состояний системы обработки транзакций

Загруженность системы обработки входящих транзакций можно определить как вероятность ненахождения системы в состоянии S ₀. Обозначим величину вероятности нахождения системы в состоянии S ₀как p ₀. Тогда будет справедливо равенство

201 p 0 = 2 p1 ,                                      (2) где 210 - интенсивность перехода системы из состояния S0; 201 - интенсивность перехода из состояния S0 в состоянии S1.

Для p ₁ справедливо выражение

2 Р 1 = 2 21 Р 2 .                                   (3)

Аналогично для p _k. В общем случае вероятность пребывания системы в состоянии определяется следующим соотношением:

2 k , k + 1 p k = 2 k + 1, k p k + 1 .                                          (4)

Тогда система уравнений примет вид

Л и p 0 = Л .0 p 1, 2 12 p 1 = 2 21 p 2,                                             , _ ' ■           -                                                 (5) 2 k , k + 1 p k = 2 k + 1, k p k + 1.

Для решения данной системы уравнений выразим все значения через p ₀. Например,

для p1 справедливо P1 =201 pо ;                                         (6) 210 для p2

_ ^X 12 „ _ ^X 12 Л и „

Р 2 =У P i = ; i Р ⁰ .                                (7)

^X 21      ^X 21 ^X 10

Следует обратить внимание, что в числителе выражения (7) стоят интенсивности, идущие слева направо (см. Рисунок 1). Эти интенсивности одинаковы для всех переходов направо и равны X , а переходы налево, которые представлены интенсивностями в знаменателе, равны ц [7]. Тогда справедливо выражение:

Г х)k

Рк =1 — I Р0 .(8)

V М )

Вероятность всех возможных n состояний

n

^Р, = 1,(9)

то есть

, х   ,Г х Y     ( х У   ,     ( x ) n ,

Р 0 +— Р 0 +| —I Р 0 +| —I Р 0 + ^ + Н1 Р 0 = ¹ .

ц    V ц )    V ц ) V ц )

Отсюда p ₀ можно найти по формуле

Р0 =.

Е П ^” [ X |

' =⁰ V ц )

В знаменателе получен ряд геометрической прогрессии

S = a(1-q) n

Числовое значение выражения (12) (то есть сумма всех членов геометрической про- грессии) находится по формуле

_ a ^{( 1 -} qn )

Sn = 1 - q ’ при n^№ и при a = 1.

Тогда выражение суммы ряда геометрической прогрессии

Решение данного предела

n lim¹ - ^- n -^w 1 — q

.

A q l < 1, ^{1 —} q

Так как интенсивность и пропускная способность не могут быть отрицательными числами, то знак модуля можно убрать. Таким образом, ряд сходится, когда выполняется условие

X<1.                                     (16)

ц

При выполнении условия (16) система обработки транзакций, представляющая из себя СМО, находится в стационарном состоянии, при этом очередь не накапливается до бесконечности, и можно рассчитать среднее время обработки транзакций.

Сравнение скорости обработки транзакций в распределенных системах ...

Для удобства обозначим величину X / Ц как р . Чтобы найти среднее время обработки транзакций, сначала найдем среднее количество устройств, находящееся в системе обработки транзакций в случайный момент времени. Для одноканальной СМО с неограниченной очередью данное значение можно найти по формуле

L cucm =       .                                        ⁽¹⁷⁾

• 1    - С

По формуле Литтла найдем среднее время обработки транзакции:

Т _о6 =

Lcucm

X

— 1

р =   t o6   =1 ¹ _— X I

X(1—р)  1—Xto6  (to6    J

Из выражения (18) можно сделать вывод, что при увеличении t _o6 увеличивается T _o6 ,

• и при увеличении X также увеличивается T _o6 .

Стоит отметить, что данная закономерность прослеживается именно на интервале области допустимых значений параметров t _o6 и X :

[ t o6 е [ 0; +» ) ,

T o6 =ре [ 0; +» ) ,                                 (19)

[ t o6 Xе [ 0;1 ) .

На Рисунке 2 представлен график зависимости T _o6 от t _o6 и X .

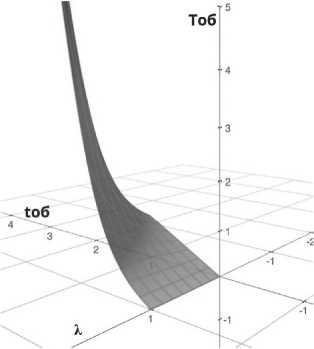
Рисунок 2. График зависимости времени обработки транзакции от t _o6 и X

Из (16) и Рисунка 2 можно сделать вывод, что для поддержания системы в стационарном состоянии необходимо ограничить число входящих транзакций, а значит, ограничить количество устройств в распределенном реестре (проявляется взаимная зависимость параметров n (количество устройств в сети) и X ). То есть n ^да , X^w , а значит, T _о6 ^^да . Из этого следует, что горизонтальное масштабирование системы с помощью увеличения количества устройств приведет к увеличению времени обработки транзакций устройствами сети.

Проблему ограниченности потока входящих заявок в распределенную систему может решить DAG – ациклический направленный граф.

Транзакции, исходящие из устройств, составляют набор узлов DAG. Множество его ребер получается следующим образом: когда появляется новая транзакция, она должна подтвердить k других транзакций для общего k ≥ 2 предыдущих транзакции; данные подтверждения представлены направленными ребрами. Чтобы создать транзакцию, пользователи-устройства должны находиться в рабочем состоянии (например, передавать данные другим устройствам) и подтверждать другие транзакции.

На Рисунке 3 представлен пример направленного ациклического графа. Вершины графа – это транзакции, а направленные дуги показывают, какие транзакции подтверждаются другими транзакциями. A, B, C, D, E, F, G, H – это обозначения набора устройств распределенного реестра. Линии перпендикулярные оси абсцисс показывают принадлежность транзакции к определенному устройству распределенной сети. По оси ординат обозначены номера транзакций в порядке добавления в DAG. Транзакции под номерами 16–18 пока не являются подтвержденными.

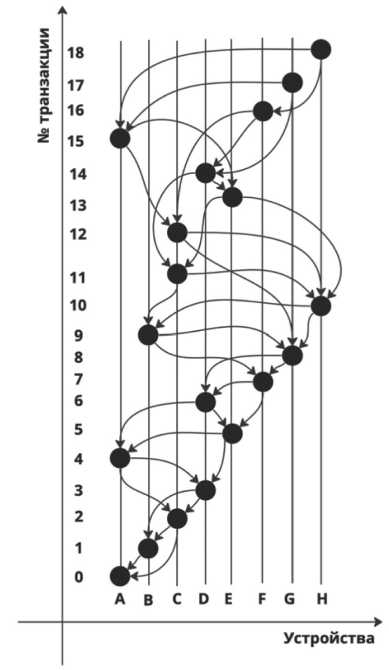
Рисунок 3. Пример ациклического направленного графа

Главное преимущество DAG по сравнению с классическим распределенным реестром в том, что система может обрабатывать транзакции в многопоточном асинхронном режиме (то есть несколько транзакций могут обрабатываться различными устройствами в несколько потоков, при этом время начала и конца обработки транзакции у различных обрабатывающих транзакцию устройств не совпадает). На Рисунке 4 серым цветом в качестве примера отмечены новые транзакции, которые поступили в систему одновременно. Данные транзакции будут обрабатываться параллельно в несколько потоков, при этом время конца обработки может не совпадать.

Сравнение скорости обработки транзакций в распределенных системах ...

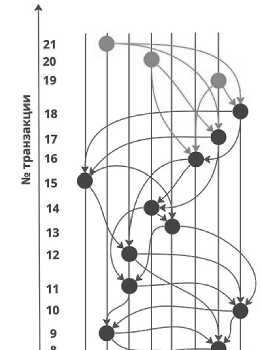
Рисунок 4. Одновременное формирование новых узлов

В соответствии с теорией массового обслуживания данная система принадлежит к классу многоканальных СМО с неограниченной очередью. Количество каналов n в данной системе будет равно количеству устройств, отправляющих транзакции.

Пусть, как и в случае с распределенным реестром, рассмотренном выше, время обработки транзакций для всех устройств в любой момент времени равно t _об, тогда в данном случае условием стационарности системы будет являться выражение (условие стационарности для многоканальной СМО)

<1.                                            (20)

n

Из (20) следует, что у сети DAG есть преимущество по стационарности в сравнении с классическим реестром в n раз, если сравнивать с выражением стационарности системы классического распределенного реестра (16).

Количество транзакций в системе обработки транзакций можно определить следующим образом:

n + 1

Lcucm = LO4 + P =     , 0 .2 + P ,                            (21)

1 P I

n ■ n !l 1I

V n)

где L_O4 - количество заявок, находящееся в очереди на обработку.

Среднее время обработки транзакции определяется по формуле (18), как и в случае с реестром. Подставив в выражение (18) результаты из формулы (21), получим выражение

То« =---(^ *, p°, + >0..                         (22)

„п,Г1 -^to.I Л

V n )

Значение p ₀ можно найти с помощью вычисления суммы модифицированного ряда геометрической прогрессии:

n ^^ i

^ У .                          (23)

i = 0 ^{1 !}

Данный ряд является степенным рядом, который сходится в значении e ^P .

Таким образом, p ₀ определяется соотношением

р e Р 0 =

( n ^да i

(t^^.

- 1

= e

р

.

В итоге получим соотношение для расчета времени обработки транзакции в распределенной сети ациклического направленного графа

T ₀6 =

( X t o6 ) n ^{+ 1}

e - Xto6

n • n

—

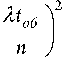
+ to6 .

X

При n ^w первое слагаемое выражения (21) будет стремиться к нулю, и T06 ^ t06 (см. Рисунок 5). По оси ординат отмечено время обработки системой относительно времени обработки транзакции отдельным устройством, по оси абсцисс – количество устройств в сети.

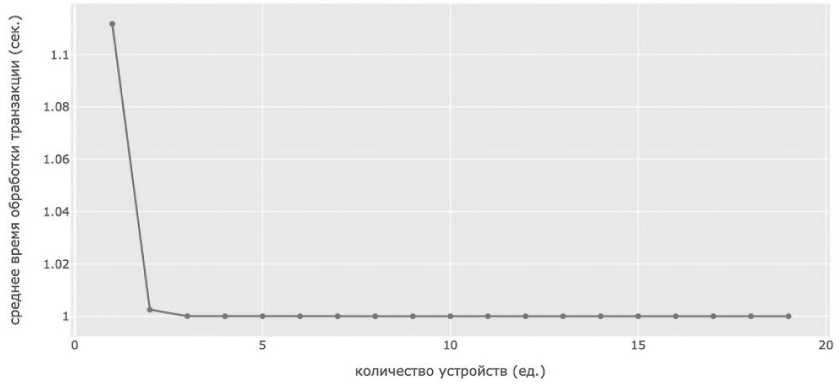
Рисунок 5. График зависимости времени обработки транзакции от количества устройств в сети DAG

В сети DAG время практически не зависит от количества устройств.

Стоит отметить, что при одной и той же величине t _обпропускная способность с ростом количества устройств в распределенном реестре остается неизменной, а в DAG увеличивается в n раз. Таким образом, в DAG становится выгодно увеличивать объем сети (см. Рисунок 6).

Если допустить, что увеличение количества устройств приведет к повышению интенсивности (что может быть обусловлено отправкой транзакций подтверждения), то получится зависимость, представленная на Рисунке 7.

Можно заметить, что для DAG большее число устройств в сети повышает ее устойчивость.

В работе были учтены такие факторы, как время обработки транзакции устройствами, интенсивность поступления транзакций в систему, количество устройств. Пропускной способностью каналов связи можно пренебречь в связи с тем, что устройства передают малые по объему пакеты данных. Тем не менее есть неучтенный незначительный фактор – время отклика устройств. Для этого проведен сравнительный анализ показателей скорости, результаты которого представлены в Таблице.

Сравнение скорости обработки транзакций в распределенных системах ...

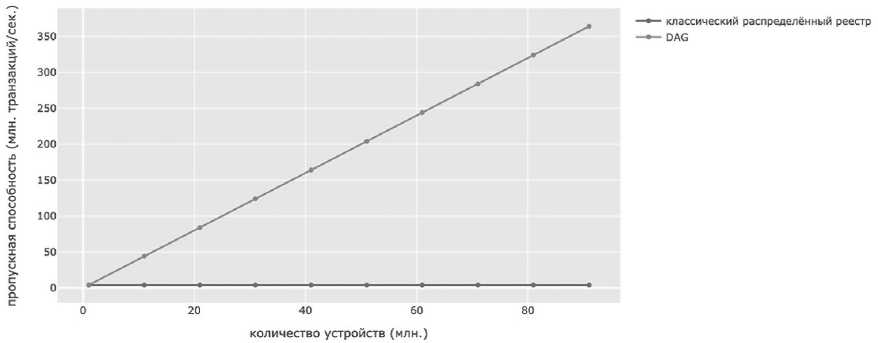
Рисунок 6. График зависимости пропускной способности от количества устройств в сети

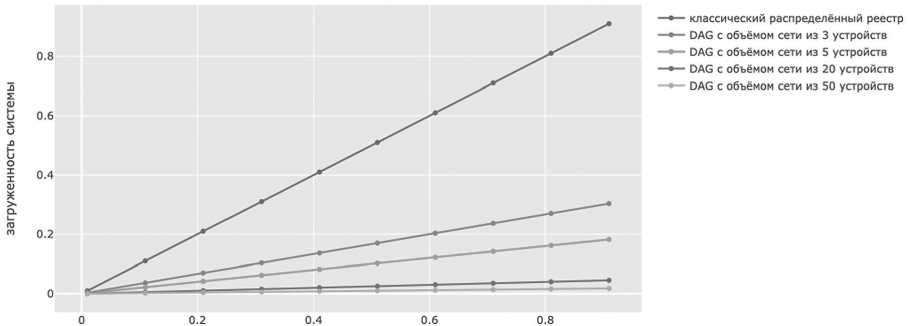
ср. время обработки транзакции одним устройством (сек.)

Рисунок 7. Зависимость загруженности системы от среднего времени обработки транзакций для различных распределенных реестров

Таблица

Показатели скорости работы распределенного реестра и ациклического направленного графа при различных величинах интенсивности

Интенсивность нагрузки	Время обработки транзакций распределенным реестром, сек.	Время обработки транзакций ациклическим направленным графом, сек.
0,1	0,006	0,005
0,25	0,007	0,005
0,5	0,011	0,006
0,75	0,018	0,006
0,9	0,081	0,007
0,95	0,126	0,007
0,99	0,708	0,007

Заключение

В работе с помощью законов теории массового обслуживания для классического распределенного реестра и ациклического направленного графа выведены формулы, по которым можно рассчитать время обработки транзакции в системе. Математически доказаны преимущества направленного ациклического графа по скорости обработки транзакций и по пропускной способности по сравнению с классическим распределенным реестром. Таким образом, переход от классического распределенного реестра к DAG может решить проблему масштабирования, так как при росте объемов транзакций данная структура только повышает свою пропускную способность.