Сравнение спектрального метода расчета открытых диэлектрических волноводов с лучевым методом и методом частичных областей

Открытые диэлектрические волноводы (ОДВ) и устройства на их основе находят широкое применение в технике СВЧ-, КВЧ- и оптического диапазонов волн. В работе [1] был предложен спектральный метод анализа открытых диэлектрических волноводов, основанный на методе интеграла Фурье [2] и модифицированном методе Галеркина [3]. Изложим основные положения указанного метода.

Рассмотрим ОДВ с произвольным поперечным сечением (рис. 1).

Функция, задающая значение диэлектрической проницаемости в каждой точке сечения, определяется следующим образом:

s ( x , y )

J s ( x , y ) , [ ^s вн , w <

I x | <  w П | y | <  h , |x | U h < | y |,

то есть в пределах поперечного сечения S ОДВ

(внутри пунктирного контура, рис. 1) диэлектрическая проницаемость задается функцией s ( x , y ) , в окружающем пространстве S_BH диэ-

лектрическая проницаемость имеет постоянное значение s_вн (область вне пунктирного контура).

Компоненты электрического поля в такой

структуре должны удовлетворять уравнениям Максвелла, скалярная форма записи которых

имеет вид

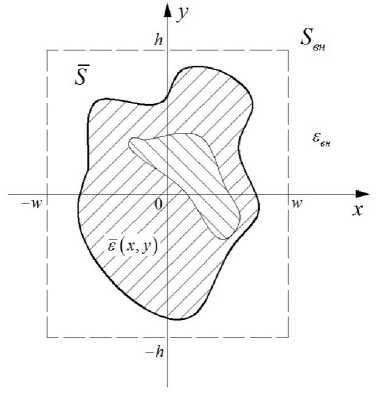
Рис. 1. ОДВ с произвольным поперечным сечением

d2 Ex d у У d2 Ey dx 2

d² Ez d x ²

+ (k0s(x, y) — e2 ) Ex

+ ( k 2 ^s( x , y ) ^— р² ) E y

+

—

—

d² E_u    8E

---^y + i p^ E z = 0; d x d y    d x

d² E_x    ._n d E_{z   n}

---x + i P —- = 0; (1) d x d y     d y

d² E                  d E_x    ^d E y

---- + k 2 s ( x , у ) E z + i P — x + i P—= 0.

d у ²                    d x      d У

Решения системы уравнений (1) представим в виде интегралов Фурье [2]:

да да

E x ( x , y ) = J J a ( p, k ) e ^— i ^{p x}e ^— i ^{K y}d p d к ;

—да —да да да

E_y ( x , y ) = J J b ( p, к ) e ^— i ^{p x}e ^— i ^{K y}d p d к ;        (2)

—да —да

да да

E z ( x , y ) = J J c ( p, к ) e ^- i ^p x e - i ^K y d p d к .

-да -да

Особенность представления полей в виде (2)

состоит в том, что компоненты электрического поля записываются независимо друг от друга со спектральными коэффициентами a (p, к) , b (p, к) и c (p, к) . Для установления связи между последними, а значит, между компонентами Ex , Ey и Ez, подставляем выражения (2) в систему (1), в результате чего получаем:

да да

• -    J J a ( p, к ) к² e ^- i ^p x e ^- i ^к y d p d к +

  -да -да

да да

• +    ( k 0 s ( x , y ) - P 2 ) J J a ( p, к ) e ^- i ^p x e ^- i ^к y d p d к +

  -да -да

да да

• +    J J b ( p, к ) p ■ к e ^- i ^p x e ^- i ^к y d p d к +

  -да -да

да да

• +    в J J ^C ( p , к ) p e ^- i ^p x e ^- i ^к y d p d к = 0;

  -да -да

да да

• - J J b ( p, к ) p² e ^- i ^p x e ^- i ^к y d p d к +

  -да -да

да да

• +    ( k 2 s ( x , y ) -в² ) J J b ( p, к ) e ^- i ^p x e ^- i ^к y d p d к +

  -да -да

да да

• +    J J a ( p, к ) p ■ к e ^- i ^p x e ^- i ^к y d p d к +

  -да -да

да да

• +    в J J ^c ( p, к ) к e ^- i ^p x e ^- i ^к y d p d к = 0;

  -да -да

да да

• - J J c ( p , к ) p 2 e ^- i ^p x e ^- i ^к y d p d к-

  -да -да

да да

• - J J c ( p, к ) к² e ^- i ^p x e ^- i ^к y d p d к +

  -да -да

да да

+ k 2 s ( x , y ) J J c ( p, к ) e ^- i ^p x e ^- i ^к y d p d к +

-да -да да да

+ в J J a ( p, к ) p e ^- i ^p x e ^- i ^к y d p d к +

-да -да да да

+ в J J b ( p, к ) к e ^- i ^p x e ^- i ^к y d p d к = 0.

-да -да

Используя равенства да

J e ^- i ^p x ■ e i ^ ^x dx = 2n-5 ( ^-p ) ,

-да да

J e-iky ■ eiZy dy = 2n-5(Z-k), -да где 5 — дельта-функция Дирака, произведем над записанной системой двумерное преобразование Фурье, то есть каждое уравнение системы (3) умножим на ei^x ■ eiZy и проинтегрируем по переменным x и y в пределах от -да до да. В ре- зультате получаем систему трех однородных интегральных уравнений Фредгольма 2-го рода относительно спектральных функций a (p, к) , b (p, к) и c (p, к) из представления Фурье (2):

4л2a (£, z) ■ (k2Sвн - в2 - z2 ) + да да          г h w

+ ko J J a (p,к) J J (s( x, y ) ^ вн) x

-да -да          - h - w x e i(p ^ xe i(к Z)ydxd,y dp dк +

+ 4n² b (^H^ + 4n² c (^, Z)-p.^ = 0;

4n2 b (^, Z).(k22s вн -в2 -^2) + да да            i- h w

+ k2 J J b (p, к) J J (^( x, y )-e вн ) x

-да -да          - h - w                            (4)

x e i ^(p ^ ) x e i ^{(к Z)} y dxdy d p d к +

+ 4n² a ( ^,ZM^ + 4n² c ( ^, Z ) -p-Z = 0;

4n2c (^,z) ■ (k02sвн -^ 2-Z2) + да да            |- h w

+ k2 J J c (p, к) J J (^( x, y )-e вн )x

-да -да          - h - w x e i(p ^) xe i(к Z)ydxdy dp dк +

+ 4n² a (^в^ + 4n² b ( ^,Z ) -P-Z = 0.

При решении этой системы неизвестные функции a ( p, к ) , b ( p, к ) и c ( p, к ) будем искать в виде разложений [3] по полиномам Эрмита с весовыми функциями:

N        («p)2 (Хк)2 a (p, к)=^ ane 2 e 2 Hkn («p) Hmn (хк); n=0 N       («p)2 (Хк)2 b (p, к)=^ bne   2 e 2 Hkn («p) Hmn (хк);(5) n=0 N       («p)2 (Хк)2 c (p, к)=^ cne   2 e 2 Hkn («p) Hmn (Хк), n=0 где N = (N + 1)2 - 1, а индексы kn и mn определяют- ся как mp+(n+1).r = p, kp+(n+1).r = r, p = 0,1,..., N, r = 0,1,...,N; а и x — масштабирующие коэффициенты, подбирая которые можно влиять на скорость сходимости представлений (5). При проведении расчетов полагаем, что а = x = 1 ko, где ko – волновое число свободного пространства. а и x вычисляются один раз для какой-нибудь одной частоты.

Подставляем (5) в систему (4). Умножаем каждое из уравнений поочередно на функции

( а^ ) ²    ( XZ ) 2

Fq (Z, Z) = e 2 e 2 Hkq «) Hmq (xZ) , q = 0,1, ... N и интегрируем по переменным £ и Z в пределах от -да до да. Используя соотношения ортогональности [4] полиномов Эрмита с весовыми функ- циями да e-(ар) Hk (ар) ■ Hk (ар) dР = nq

-да

0,

2 ^kq k q !

^п          , ^kn = ^kq ,

а kn * kq;

да да

j J e ^(ар) e ^(xk) H k n ( ар ) H m n ⁽ x^{k ) X}

-да -да х Hkq (°Р) Hmq (xK) dРdк =

2 ^{kq +} m q k ! m !

- 1% q = „----------,

= I               «x n = q,

0, n * q, получаем СЛАУ относительно неизвестных ко эффициентов разложения an, bn и cn n = 0,1,..., N:

4П² ( ( k g2 _e вн -в² ) ^- I ) + k g ² W

4n² K

4 п 2 в J

4n² K

4n² ( ( k 2 _e вн -в² ) ^- I ) + k 2 W

4п²в J

4п²в J

4п²в J

4n² ( k 2 _S вн %- I - I ) + k²2 W

a

■ b

c

= 0,

где в — продольное волновое число. Матрица системы имеет размерность 3( N + 1)² х 3( N + 1) 2 . Приравнивая ее определитель нулю, получаем

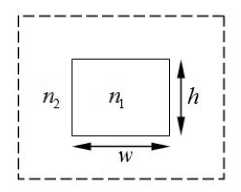
Рис. 2. Геометрические размеры поперечного сечения полоскового волновода

спектральный метод лучевой метод

h=4 мкм, w=3 мкм

EM

HE®

EH®

HEm

I*

+

t

t

,t

t

t

t 1

t

ЕНж

f, ТГц

Рис. 4. Дисперсионные характеристики первых пяти волн полоскового волновода мо сначала найти корни дисперсионных уравнений волн симметричных пленочных волноводов с толщиной w и h.

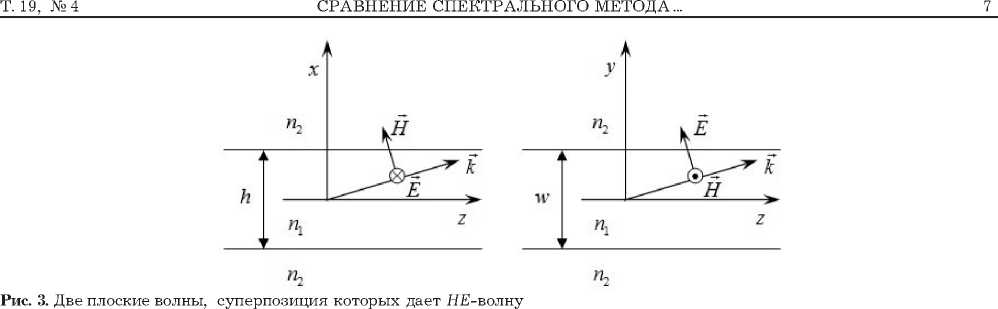
В качестве примера рассмотрим алгоритм расчета дисперсионных характеристик волн HE_mn с четным индексом m и нечетным индексом n . Ориентацию осей x и y выбираем так, как показано на рис. 3. На фиксированной частоте находим корни в н дисперсионного уравнения волн H_m симметричного слоя с толщиной h

Uh ■ tg (Uh/2) = VH , (6) где uH = hko^ln2 - pH , vH = hko^eH - n2 . (7) вh в выражениях (7) — нормированное на ko продольное волновое число, uH и vH – нормированные на ko поперечные волновые числа в полоске и окружающей его среде, соответственно. Уравнение (6) соответствует четным m (волнам с четными и нечетными индексами соответствуют [5] различные дисперсионные уравнения).

Затем находим корни в e дисперсионного уравнения волны E_n симметричного слоя с толщиной w (индекс n – нечетный):

-VE ■ tg (uE/2) = uE (n2 /ni )2, где uE = wko^n! - pE , vE = wkoл]pE - n2 .

Определив в h и в e , находим соответствующие им значения u_H , u_E и подставляем их в формулу, связывающую волновые числа:

22  2

в = Vn1 - uH - uE , где в — нормированное на ko продольное волновое число волны HEmn с четным индексом m и нечетным n.

На рис. 4 приведены дисперсионные характеристики первых пяти волн полоскового волновода. Расчет производился двумя методами — спектральным (полагалось, что N = 14) и лучевым. Из рис. 4 видно, что два метода дают хорошее совпадение в области высоких частот.

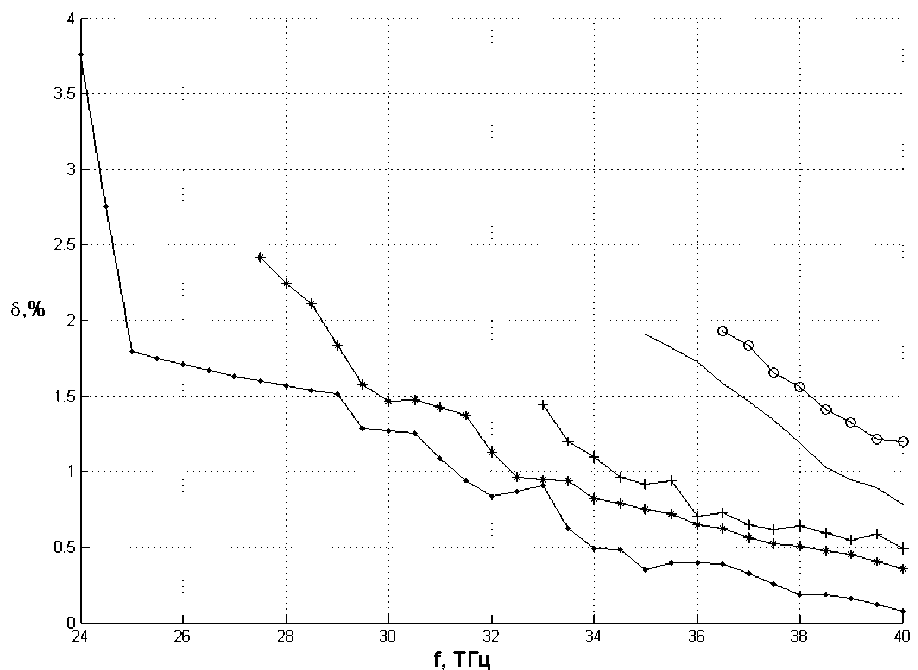
Рис. 5. Относительное расхождение между коэффициентами замедления для волн, дисперсионные характеристики которых рассчитаны двумя методами (рис. 4)

В приближении к критическим частотам расхождение увеличивается.

Классификация волн была произведена с помощью лучевого метода. Однако, на более высоких частотах классификация волн становится затруднительной, так как для определения дисперсионных характеристик приходится решать целых восемь дисперсионных уравнений, которые, вообще говоря, позволяют различать НЕ и ЕН- волны, а также устанавливать четность, либо нечетность одного из индексов. Для определения же порядка следования индексов нет никакой дополнительной информации.

Для численной оценки расхождения, даваемого двумя методами, воспользуемся выражением:

δ = βSPEC - βRAY100%, βHE где βSPEC и βRAY – коэффициенты замедления, рассчитанные спектральным и лучевым методами, соответственно; βHE – коэффициент замедления основной волны, рассчитанный спектральным методом (для основной волны параметр βSPEC совпадает с βHE). Зависимость параметра δ от частоты для первых пяти волн полоскового волновода (рис. 4) представлена на рис. 5.

Из рис. 5 видно, что погрешность лучевого метода возрастает с увеличением номера волны. Она (погрешность) связана с тем, что в приближении лучевой модели плоские волны, образующие поле, рассматриваются попарно независимо: не учитывается взаимодействие плоских волн взаимно ортогональной поляризации. Тем не менее, на высоких частотах оба метода дают хорошее совпадение.

Для основной волны в области низких частот сравниваемые методы дают не только количественное, но и качественное отличие. Это связано с тем, что на низких частотах перестает выполняться условие применимости лучевого подхода [5]: h ; w >> λ.

Таким образом, за исключением низкочастотной области лучевой метод при расчете полосковых световодов дает вполне достоверные результаты. В СВЧ-диапазоне целесообразно использовать волновой подход. Можно сделать вывод, что лучевой метод является действенным в оптическом диапазоне, то есть когда полосковые ДВ являются световодами.

Сравнение спектрального метода с методом частичных областей

В современных телекоммуникационных системах широкое распространение получили многослойные волоконные световоды с круглым поперечным сечением. Для расчета таких световодов в работе [6] предложен эффективный метод, позволяющий избежать вычисления определителей плохо обусловленных матриц. Метод является строгим, поэтому его можно использовать для проверки спектрального метода.

В качестве примера рассмотрим световод с поперечным сечением, представленным на рис. 6.

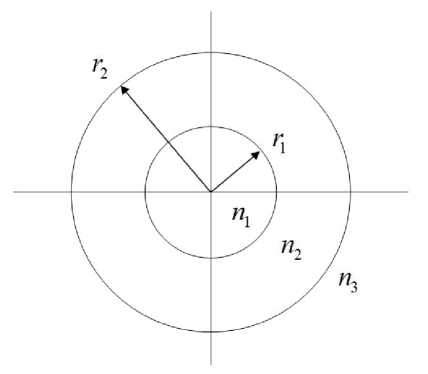
Рис. 6. Поперечное сечение трехслойного ОДВ

Зададимся следующими параметрами:

• — r = 1 мкм, Г 2 = 2 мкм;

• - п 1 = 1.48 , n ₂ = 1.1418 , n 3 = 1.45.

В этом случае рассматриваемый световод имеет W -образный профиль показателя преломления (такие световоды называются световодами с депрессированной оболочкой).

Использование спектрального метода для расчета дисперсионных характеристик таких ОДВ предполагает вычисление двукратных интегралов по круговой области. В [7] приводится формула для вычисления таких интегралов:

JJ f ( x , У ) dxdy =

C

= n a

г 1               10

■  ~ f (0, °)+^^ p1 mf (x1 m, y1 m ) + u           m=1

⁺ ^^ ^p 2 m f ^{( x} 2 m , ^y 2 m )

m = 1

+ o ( a ¹⁰ ) ,

в которой коэффициенты p1m , p2m и координаты ( x1 m, У1 m ) , ( x2m, У2m ) вычисляются по форму лам:

/6 - V6

x =

1 m V 10

6 - V6   . [ 2 nm )

y =          a sin ;

^{1 m} V 10 I 10 )

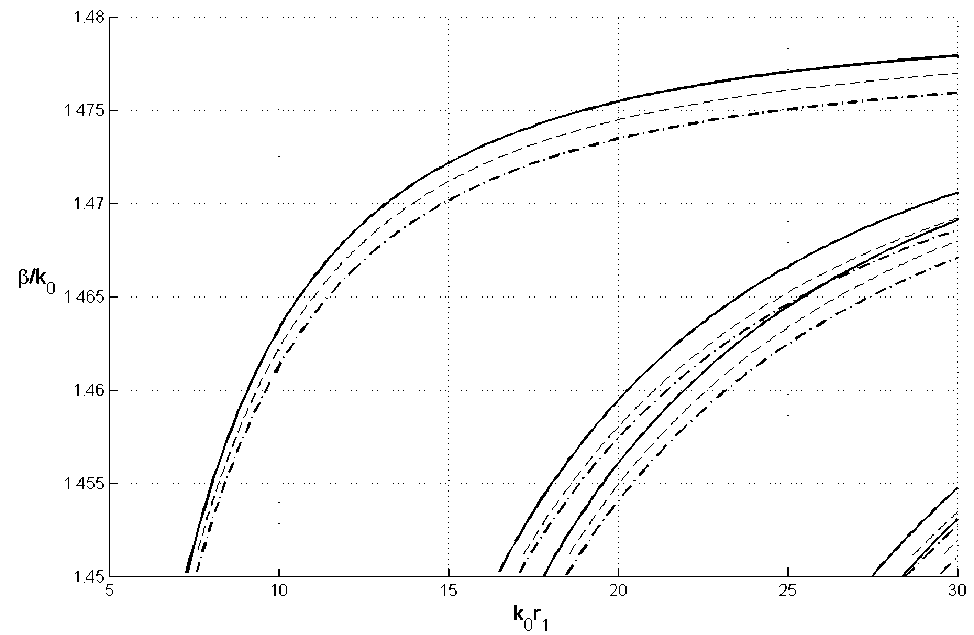
Рис. 7. Дисперсионные характеристики гибридных волн ОДВ с азимутальным индексом n = 1

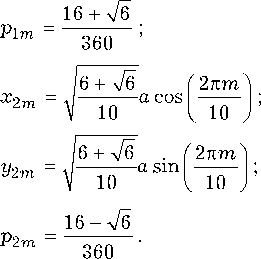
a – радиус круговой области.

На рис. 7 сравниваются дисперсионные характеристики гибридных волн с азимутальным индексом n = 1, полученные двумя методами. Чтобы не загромождать рисунок, дисперсионные характеристики симметричных волн и волн с азимутальными индексами n > 1 не показаны. Сплошной линией показаны зависимости, полученные путем строго расчета [6]. Штрих – пунктирной и пунктирной линиями показаны дисперсионные характеристики, полученные спектральным методом при N = 6 и N = 9, соответственно.

Из рис. 7 видно, что для волн высших типов спектральный метод дает более медленную сходимость, по сравнению с основной волной. Тем не менее, уже при N = 14 дисперсионные характеристики, рассчитанные двумя методами, становятся графически неразличимы, как для основной волны, так и для других гибридных волн. Полученный на тестовом примере результат подтверждает действенность спектрального метода.