Сравнительная оценка методов кластеризации в работе с большими данными

В сфере информационных технологий на данный момент активно применяется термин Big Data или "Большие данные". Единого общепринятого определения данному понятию не существует. Наиболее правильным и полным, на наш взгляд, является такое: комплекс методов, средств и научно обоснованных подходов к анализу больших массивов данных с целью использования в практической деятельности, то есть, по сути, технология обработки и анализа непрерывно стремительно поступающих огромных массивов разнородной информации.

Big Data представляет собой структурированные и неструктурированные данные большого объема, а также инструменты для работы с ними, что предоставляет возможности для широкого их использования в различных народнохозяйственных сферах, таких как финансы, здравоохранение, маркетинг, средства массовой информации.

Исходя из определения, при таких параметрах входных данных возникает проблема их корректной фиксации, систематизации, обработки, анализа и хранения, для чего и применяются методы кластерного анализа, которые могут выступать в качестве именно начального шага в работе ввиду того, что эти алгоритмы опираются, прежде всего, на такую характеристику Big Data, как мощность рассматриваемого озера всех типов "сырых" данных, так называемый размер входа n [1]. Такие методы могут быть полезными лишь для предварительного анализа, поскольку позволяют учесть специфику больших данных в оценке лишь по одному, рассматриваемому ниже параметру – сложности алгоритмов.

Сложность алгоритма – это количественная характеристика, которая говорит о том, сколько времени либо какой объем памяти потребуется для его выполнения.

При анализе сложности для класса таких задач определяется некоторое число, характеризующее некоторый объем данных – размер входа n.

Таким образом, полагаем, что сложность алгоритма – некоторая функция размера входа. Сложность алгоритма, очевидно, может быть различной при одном и том же размере входа, но различных входных данных.

Понятие "О-сложность" алгоритмов введено для того, чтобы измерять скорость роста функции в зависимости от входных данных [2]. В математике "O" используется для обозначения "order of" (порядка) и позволяет сравнивать функции роста для оценки верхней границы (наихудшего случая), временной сложности алгоритма.

Кроме очевидной экономии различного рода ресурсов, временных и аппаратных, и ускорения процесса обработки больших объемов непрерывно поступающей информации, кластеризация может дать базовые представления о закономерностях внутри таких данных.

Кластеризация – задача разбиения заданной выборки объектов на непересекаю-щиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались. Под схожестью обычно понимается близость друг к другу относительно выбранной метрики. Для осуществления данного процесса применяются специальные разработанные алгоритмы кластерного анализа. Однако не существует универсального алгоритма, и поэтому возникает необходимость понимания, в каких случаях какой подход предпочтительнее.

В связи с этим подробно рассмотрим наиболее известные алгоритмы и сделаем вывод относительно их применимости в сфере больших данных.

Иерархическая кластеризация

Данный метод основан на построении иерархической структуры кластеров, представленной в виде дерева или дендрограммы. (рис. 1).

Данный метод включает в себя два типа – агломеративный и дивизивный (англ. divisive).

Агломеративный вариант работает по принципу от меньшего к большему, т. е. процесс начинается с каждого объекта в собственном кластере и последовательно проводится объединение ближайших кластеров до тех пор, пока все объекты не окажутся в одном кластере.

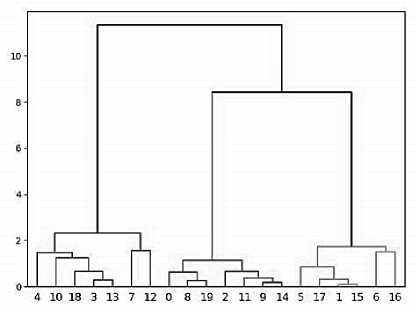
Рис. 1. Итог работы иерархического метода кластеризации

В случае дивизивного типа действуют наоборот: начинают с одного кластера, а затем разделяют его на более мелкие.

Для работы данного алгоритма требуется решить, какие данные между собой следует объединять в кластеры, для этого выбирается метрика, количественно характеризующая сходство или несходство данных между собой [3].

Одними из наиболее применимых метрик являются евклидово d(p,q')(1) и манхэттенское d (2) расстояния:

d(p, q} = ^Z^pPk—qk^(1)

d = lx2 -%i| + \У2 — У1| .(2)

Основными преимуществами данного алгоритма являются наглядная визуализация результатов, что означает высокую интерпретируемость, а также отсутствие необходимости вручную задавать необходимое количество кластеров, так как алгоритм строит все доступные уровни иерархии.

Алгоритмическая сложность данного алгоритма кубическая, то есть равна O(n3).

Это означает, что время выполнения алгоритма пропорционально кубическому объему входных данных и будут требоваться значительные аппаратные мощности.

Нельзя не отметить низкую устойчивость алгоритма к шумам и выбросам, то есть к появлению точек, не принадлежащих ни одному из кластеров и экстремально отличающихся от остального массива заданных точек, например отрицательное число в массиве положительных.

Также стоит сказать о невозможности визуализации работы алгоритма в виде разбиения на кластеры как произвольной, так и какой-либо фиксированной геометрической формы, к примеру, круга или сферы, за исключением дендрограммы, а также чувствительности алгоритма к метрике расстояний. Под чувствительностью к метрике подразумевается вероятность получить разные результаты в зависимости от выбора той или иной метрики.

Как итог, можно сделать вывод о нецелесообразности использования рассматриваемого алгоритма при работе с большими данными.

K-means

Данные алгоритмы кластеризации представляют собой группу алгоритмов на основе центроидов. Центроид – средняя точка или центр массы фигуры или множества заданных точек.

Суть алгоритма k-means заключается разбивке данных на k точек, где k – заданное количество кластеров и каждый кластер представляет собой группу точек, центр которых является центроидом (рис. 2) [4].

Clusters of customers

Careful Standard

Target Careless Sensible Centroids

20       40       60       80      100     120      140

Annual Income (kS)

Рис. 2. Визуальное представление алгоритма k-means

Получение масштабируемых алгоритмов основано на идее отказа от локальной функции оптимизации. Парное сравнение объектов между собой в алгоритме k-means есть не что иное, как локальная оптимизация, так как на каждой итерации необходимо рассчитывать расстояние от центра кластера до каждого объекта.

Данный алгоритм является довольно простым в реализации, также он легко масштабируется. Но в то же время его применение ведет к большим вычислительным затратам.

Также имеется ряд минусов, таких как слабая устойчивость к шуму, чувствительность к задаваемым параметрам и начальным центроидам, необходимость задавать число нужных кластеров, строгая форма кластеров сферической формы.

Алгоритмическая сложность алгоритма является плавающей величиной, она оценивается как O(k×n×t), где k – количество центроидов, n – общее количество точек, а t – количество итераций, и чаще всего, в том числе и в случаях значительного увеличения потока данных, она является полиномиальной.

Как итог, можно утверждать, что применять данный алгоритм при обработке больших данных нерационально.

DBSCAN

DBSCAN – алгоритм кластеризации, основанный на плотности, который используется для разделения наборов данных на группы, основанные на пространственной близости точек (рис. 3) [5]. Под плотностью понимается количество точек в заданном пространстве.

Для работы алгоритма требуется задать два параметра необходимых для создания кластеров – "eps" (радиус окрестности в которой ищутся соседи) и "min_samples" (минимальное количество точек, необходимое для определения кластер.

DBSCAN обладает следующим рядом преимуществ: автоматическое определение количества кластеров, возможность создания кластеров произвольной формы, устойчивость к шуму и простота реализации.

Но у него есть такие минусы как чувствительность к параметрам eps и min_samples.

В лучшем случае алгоритмическая сложность DBSCAN будет линейнологарифмической. Время выполнения алгоритма, очевидно, растет быстрее, чем линейно, но медленнее, чем квадратично: O(n×log n), в худшем случае она составляет O(n2), такая сложность будет получена, если не будут использоваться пространственные индексы [6].

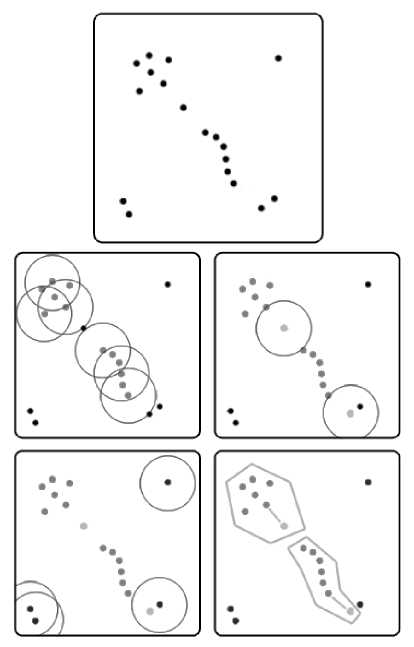
Рис. 3. Визуальное представление алгоритма DBSCAN

Пространственные индексы – структуры данных, используемые для оптимизации выполнения запросов, которые требуют доступа к пространственным объектам, таким как точки, линии, полигоны и т. д.

Исходя из вышеизложенного, мы можем сделать вывод, что данный алгоритм вполне применим для работы с большими данными, однако лишь в том случае, если будут созданы пространственные индексы для точек, что существенно сократит время его выполнения.

OPTICS

Данный алгоритм, так же, как и DBSCAN, основан на плотности.

OPTICS работает путем построения графа достижимости, который представляет собой граф, где вершинами являются точки данных, а ребрами – расстояния между ними (рис. 4).

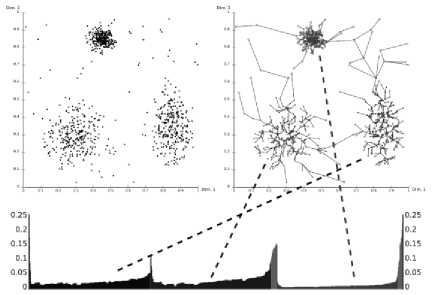
Рис. 4. Визуальное представление алгоритма OPTICS

Алгоритм затем упорядочивает точки в зависимости от их достижимости, которая определяется как максимальное расстояние до ближайшей точки с более низкой плотностью [7].

Кластеры определяются как связные компоненты в графе достижимости, где связность определяется порогом достижимости. Под порогом достижимости понимается максимальное расстояние, на котором две точки могут быть связаны и считаться частью одного кластера.

Говоря о преимуществах данного алгоритма, следует отметить его универсальность по отношению к различным типам данных, высокую устойчивость к шуму, но, будучи алгоритмом того же типа что и DBSCAN, он сильно зависит от параметров "eps" и "min_samples", и он более сложен в интерпретации.

Говоря об алгоритмической сложности, мы можем сказать, что по данному параметру он аналогичен DBSCAN, то есть она колеблется от O(n×log n) до O(n2) в зависимости от того, использовали мы пространственные индексы или нет, но, если сравнивать OPTICS и DBSCAN, то, в целом, первый будет быстрее на больших наборах данных [8].

В итоге мы можем сделать вывод, что данный алгоритм – наиболее предпочтительный для работы с большими данными из всех вышеперечисленных вариантов.

CURE

CURE – частный случай иерархической кластеризации, который использует набор представителей для определения принадлежности объекта к определенному кластеру (рис. 5) [9].

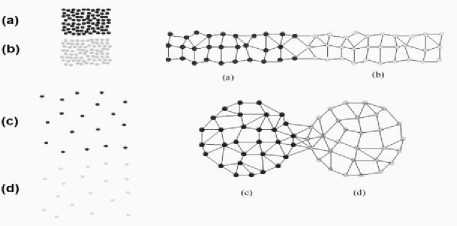
Рис. 5. Визуальное представление алгоритма CURE

Он хорошо подходит для кластеризации наборов числовых данных, особенно в случаях, когда:

• •    присутствуют выбросы: CURE менее чувствителен к выбросам, чем другие алгоритмы кластеризации;

• •    кластеры имеют сложную форму: CURE способен находить кластеры произвольной формы, а не только сферические или эллиптические;

• •    кластеры имеют разный размер: CURE может обнаруживать кластеры разных размеров, что не всегда возможно в случае других алгоритмов.

Алгоритмическая сложность фиксированная, не плавающая, составляет O(n×log n), а к преимуществам нужно отнести масштабируемость, устойчивость к выбросам и создание кластеров произвольной формы, но, к сожалению, он сложен в реализации и так же, как и DBSCAN и OPTICS, зависим от параметров [10].

Будучи алгоритмом, специально созданным для обработки больших данных, он наиболее предпочтителен при их обработке.

Суммируя ранее сделанные выводы, приведем сравнение представленных алгоритмов по следующим критериям:

• a)    преимущества;

• b)    недостатки;

• c)    сфера применения;

• c)    алгоритмическая сложность.

Иерархическая кластеризация

• a)    простота реализации, наглядность;

• b)    нежелательность использования на больших объемах данных, чувствительность к метрике расстояний, неспособность формировать произвольные формы кластеров;

• c)    биоинформатика, бизнес, обработка изображений, поиск информации;

• d)    O(n³).

k-means

• a)    простота реализации, предпочтительность применения на малых объемах данных;

• b)    низкая устойчивость к шуму, невозможность формировать произвольные формы кластеров;

• c)    сегментация клиентов, классификация документов, анализ записей звонков;

• d)    O(k×n×t).

DBSCAN

• a)    устойчивость к шуму, находить кластеры произвольной формы и разного размера, простота реализации;

• b)    чувствительность к выбору параметров, невозможность находить кластеры иерархической структуры;

• c)    медицина, анализ географических данных [11];

• d)    от O(n×log n) до O(n²).

OPTICS

• a)    устойчивость к шуму, находить кластеры произвольной формы и разного размера, простота реализации;

• b)    чувствительность к выбору параметров, невозможность кластеры иерархической структуры;

• c)    анализ геоданных, биоинформатика, телекоммуникации;

• d)    от O(n×log n) до O(n²).

CURE

• a)    устойчивость к шуму, находит кластеры произвольной формы и разного размера;

• b)    чувствительность к выбору параметров, сложность реализации;

• c)    обработка изображений, медицина, финансы [12].

• d)    O(n×log n).

Заключение

На основе проведенного анализа сделаем вывод, что среди представленных алгоритмов кластеризации наиболее предпочтительными при работе с большими данными являются DBSCAN, OPTICS и специально созданный для их обработки CURE.