Сравнительная оценка методов расчета открытых диэлектрических волноводов с произвольным поперечным сечением

Открытые диэлектрические волноводы (ОДВ) и устройства на их основе находят широкое применение в технике СВЧ-, КВЧ- и оптического диапазонов волн [1; 2], поэтому задача расчета характеристик волн ОДВ со сложной формой поперечного сечения является весьма актуальной. В настоящее время для расчетов спектра волн ОДВ привлекаются приближенные методы геометрической оптики [3–5], используются приближенная модель Гоэлла [3; 6], модель Веселова – Шлоссера, основанная на замене ОДВ экранированным ДВ с удаленной экранирующей поверхностью [3; 7]. Рассмотрим кратко суть этих методов и укажем их недостатки.

Для приближенного расчета ОДВ может быть применена лучевая модель [3–5], описывающая распространение светового потока с позиций геометрической оптики. Распространение света при этом описывается на основе траектории одного из световых лучей, которая формируется полным внутренним отражением от границ раздела сред с разными показателями преломления. Достоинство метода в том, что в ряде случаев есть возможность получить аналитическую запись дисперсионных уравнений, которые, тем не менее, будут являться приближенными.

Однако использование лучевого метода ограничено условием применимости геометрической оптики, согласно которому геометрические размеры волновода должны намного превосходить длину волны излучения. Для градиентных волноводов [3; 8] накладывается дополнительное условие: показатель преломления должен слабо изменяться в пределах длины волны. Только в этом случае удается получить аналитические представления дисперсионных уравнений. Реальные ОДВ часто не удовлетворяют требованиям геометрической оптики, поэтому их лучевой анализ может носить лишь качественный характер. Еще один недостаток лучевой модели состоит в том, что она не учитывает взаимодействие плоских волн, образующих моды ОДВ.

В модели Веселова – Шлоссера [3; 7] диэлектрический волновод помещается в соосный идеально проводящий экран. Расчет такой структуры проводится на основе метода частичных областей (МЧО). Согласно МЧО [9] рассматриваемая экранированная структура разбивается на отдельные области, для каждой из которых формулируется краевая задача на основе уравнения Гельмгольца относительно продольных компонент векторов Герца. Решения, полученные с учетом нулевых граничных условий на идеально проводящих стенках, содержат неизвестные постоянные коэффициенты. Сшивание полей на границах выделенных областей приводит к бесконечной системе линейных однородных алгебраических уравнений (СЛАУ) относительно неизвестных коэффициентов разложения поля. Дисперсионное уравнение получается © Раевский С.Б., Седаков А.Ю., Титаренко А.А., 2016

путем приравнивания нулю определителя этой системы. В предположении, что при достаточном удалении экрана направляющая структура ведет себя как ОДВ, полученное дисперсионное уравнение может рассматриваться как дисперсионное уравнение волн ОДВ. Нестрогость и определенная некорректность такой постановки задачи заключается в том, что введение экранирующей поверхности предполагает наличие нулевых граничных условий, которые не могут быть удовлетворены никаким экспоненциально спадающим полем.

Модель Гоэлла [3; 6] основывается на разложении полей в ряды по цилиндрическим функциям: поле внутри волновода представляется в виде ряда по функциям Бесселя, вне его – по функциям Ханкеля. Для составления дисперсионного уравнения и определения коэффициентов разложения используется метод коллокаций: тангенциальные составляющие поля на границе раздела сред сшиваются в N точках (узлах коллокации), число которых определяет порядок получаемой СЛАУ относительно коэффициентов разложения поля. К достоинствам данного метода следует отнести сравнительную простоту его алгоритмизации, однако, как указано в [6], данный метод применим лишь при невысоком значении диэлектрической проницаемости волновода и при выполнении определенных геометрических соотношений в пределах поперечного сечения ОДВ. Более того, данный метод обеспечивает точное выполнение граничных условий только в узлах коллокации. При этом не существует четко обоснованных рекомендаций касательно выбора расположения этих узлов. По сути, метод является интерполяционным и не предполагает строгого решения.

В работах [10–12] рассмотрен ряд численных и аналитических методов, позволяющих производить расчет слабонаправляющих ОДВ. Ключевым в теории таких волноводов является скалярное уравнение [12]:

52v 32v

—7 + —-V Vb v = - V f (^, n)v , (1) d^2 dn где под v понимается поперечная компонента электрического поля волноводной моды; ^ = xM-1, n = yM-1; M — масштабный фактор, характеризующий поперечный размер волновода. При записи данного уравнения использовано представление диэлектрической проницаемости в виде

^s ( x , У ) = ^s _s + ^s R ^f ( ^ n ) , где s _s и s r — соответственно комплексная и вещественная константы; f ( £ , n ) — функция, удовлетворяющая условию f ( £ , n ) ^ 0 при р = ^^ + n 2 ^ ^да . В приведенном уравнении фигурируют также параметры V = k y M sRr , b = y(s r , Y = в 2 / k 2 , где в — продольное волновое число. В работе [12] предлагается метод интегрального уравнения, который позволяет решать уравнение (1) даже для волноводов, описываемых комплексной функцией f ( ^ , n ) . Однако, данный метод принципиально применим только для слабонаправляющих ОДВ, что ограничивает область его использования.

Расчет ОДВ с произвольным распределением диэлектрической проницаемости по поперечным координатам на строгом электродинамическом уровне может быть произведен с помощью численных метода конечных элементов [13–16]. Однако практическая реализация данного метода сопряжена со значительными вычислительными трудностями [13; 16].

Таким образом, все перечисленные методы имеют те или ограничения, основным из которых является слабонаправляемость структуры. Только конечно-разностные методы дают универсальный подход к расчету ДВ с произвольным неоднородным поперечным сечением. Но при этом неизбежно встает проблема больших временных затрат, что затрудняет решение задач проектирования и синтеза функциональных узлов устройств СВЧ-, КВЧ- и оптического диапазонов волн.

В работе [17] предложен спектральный метод анализа открытых диэлектрических волноводов, основанный на методе интеграла Фурье [12; 18] и модифицированном методе Галеркина [19– 21]. Этот метод отличается высоким быстродействием и позволяет производить обоснованный расчет регулярных открытых диэлектрических волноводов с произвольным распределением диэлектрической проницаемости по поперечной координате. Метод является универсальным и позволяет рассчитывать ОДВ с любой геометрией поперечного сечения и высокими значениями диэлектрической проницаемости по сравнению с диэлектрической проницаемостью окружающего пространства.

В настоящем докладе ставится задача расследовать возможности предложенного в работе [17] метода и разработать рекомендации по его

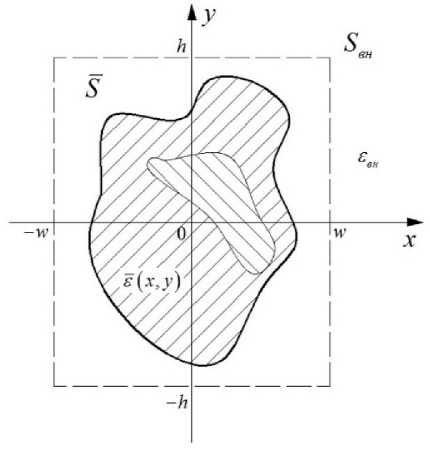
Рис. ОДВ с произвольным поперечным сечением

б( X, у)

J б ( X , y ) , [б вн , w <

I x | <  w П | y | <  h , |x | U h < |y |,

то есть в пределах поперечного сечения S ОДВ (внутри пунктирного контура, рис.) диэлектрическая проницаемость задается функцией б ( x, у ) , в окружающем пространстве S_BH диэ-

лектрическая проницаемость имеет постоянное значение б вн (область вне пунктирного контура).

Компоненты электрического поля в такой

структуре должны удовлетворять уравнениям Максвелла, скалярная форма записи которых

имеет вид:

EX + (k2s( x, у ) — p2) Ex — ду     х                ’

—

д ² E^    5Е

---y + ie^Ez = 0; дx ду     д x

применению к расчету ОДВ со сложными поперечными сечениями.

Целесообразность проводимого рассмотрения заключается в:

– проверке действенности метода для расчета ОДВ сложного поперечного сечения, с большим числом точек геометрических сингулярностей;

– исследовании характеристик ОДВ с расширенным числом степеней свободы;

– проверке плавности предельного перехода от крестообразного ОДВ, как волновода со множеством точек геометрических сингулярностей, к прямоугольному ОДВ, гарантирующей корректность и общность алгоритма;

– расчете новой направляющей структуры типа двойного гребневого волновода (ОДВ с крестообразным поперечным сечением) как базовый для построения функциональных узлов СВЧ- и КВЧ-диапазонов;

В настоящей работе спектральный метод использовался также для проверки точности лучевого метода как достаточно простого и физически наглядного.

Составление алгоритма расчета характеристик ОДВ спектральным методом

Изложим суть спектрального метода, предложенного в работе [17]. Рассмотрим ОДВ с произвольным поперечным сечением (рис.).

Функция, задающая значение диэлектрической проницаемости в каждой точке сечения, определяется как:

—у + (k2s( x, у ) — в2) Еу — д x х'

—

д2Еж   .D дEzп

---x + i в — z = 0; д x д у

д2Е7 д2Е7, 2

1гт + ^iz + k0s( x, у) Ez +

д x    ду дЕ     дЕ

• + i p^ E x + i в — ^у = 0.

• д x     д у

Метод отличается высоким быстродействием и позволяет производить высокоточный расчет характеристик ОДВ. Так, для компьютера на базе процессора Intel Core i5 с тактовой частотой 2.67 ГГц время расчета дисперсионных характеристик составило порядка 1,5 минут (полагалось, что N = 14).

Полученные численные результаты позволили выявить ряд особенностей дисперсионных характеристик волн крестообразного ОДВ. В частности, было установлено, что путем из- менения геометрических размеров поперечного сечения этого ОДВ, а также выбором функции распределения диэлектрической проницаемости по поперечному сечению, возможно увеличить область одномодовости ДВ по сравнению с полосковым волноводом. Варьирование параметров крестообразного ОДВ приводит к качественным изменениям в поведении дисперсионных характеристик. По сравнению с полосковым волноводом, на характеристиках волн высших типов крестообразного ДВ имеются точки перегиба, в которых коэффициент дисперсии d2в/dto2 (здесь в не нормировано) обращается в нуль, поэтому из выражения для групповой скорости

• 1    _ d p

Upp   dto получаем

d2P _ d Г 1 ) _^ durp _ 0dto2   d to(urpj     v2p dto      , то есть значение групповой скорости волн в точках перегиба достигает экстремума. Для полоскового ДВ такую особенность можно отметить только у основной волны.

Учитывая быстродействие разработанного алгоритма, а также его применимость для расчета дисперсионных характеристик ОДВ с большим числом степеней свободы, рекомендуется использовать его для решения задач синтеза.