Сравнительно-аналитическая характеристика показателей рассеивания при стрельбе различными боеприпасами

Двадцатое столетие характеризовалось большим количеством вооруженных столкновений по всему миру, поэтому военная инфраструктура стран в этот период развивалась очень стремительно. Каждое государство пыталось занять лидирующую позицию, улучшая и модернизируя свое вооружение, военную технику и техническое оснащение.

Одним из наиболее распространенных видов оружия того времени являлся миномет, поскольку он применим для поражения как живой силы противника, так и легкобронированной техники, а также легких фортификационных сооружений. Кроме того, минометы в сравнении с другими артиллерийскими орудиями очень мобильны, что позволяет использовать их в труднодоступных местах, где невозможно применить другие типы артиллерийского вооружения.

В данной работе были рассмотрены выстрелы к минометам трех стран: России, США и Франции. Все снаряды к ним имеют калибр 120 мм.

Российский миномет «Нона-М1» с осколочно-фугасным снарядом ЗВОФ68 характеризуется следующими параметрами [3]:

• •    угол бросания – 60^о;

• •    угол поворота – 8^о;

• •    начальная скорость полета снаряда – 367 м/с;

• •    масса снаряда – 16,1 кг.

Характеристики американского миномета М-120 со снарядом М933 [4]:

• •    угол бросания – 65^о;

• •    угол поворота – 14^о;

• •    начальная скорость полета снаряда – 310 м/с;

• •    масса снаряда – 13,2 кг.

Параметры для французского миномета МО-120-RT-61 со снарядом PRAB [5]:

• •    угол бросания – 55^о;

• •    угол поворота – 14^о;

• •    начальная скорость полета снаряда – 315 м/с;

• •    масса снаряда – 18,6 кг.

Траектория полета снаряда определяется большим числом параметров, значения которых при каждом выстреле несколько отличаются от значений, полученных при ранее проведенных выстрелах.

Вследствие этого конкретная траектория всегда отличается от предыдущей. Это несовпадение траекторий однотипных снарядов выстреливаемых из одного оружия при одинаковых расчетных условиях называется рассеиванием.

Характеристики же рассеивания (кучности) являются одним из основных показателей эффективности стрельбы. Для их определения используются опытные значения этих характеристик, получаемые для отстрелянной группы по формуле [1]:

В^ = 0.6745

N

Ж -5 ) i = 1

N - 1

где В^ - статистическая оценка вероятного (срединного) отклонения точек падения по координате £=x, z.

Чтобы более наглядно представить процесс выстрела из каждого рассматриваемого орудия, в программной среде MatLab была создана баллистическая модель, учитывающая характеристики данных орудий и математическую модель атмосферы. С ее помощью в процессе имитации стрельбы были построены вертикальная и горизонтальная траектории движения снаряда, а также получены следующие характеристики рассеивания:

• •    характеристика рассеивания снарядов по дальности ^Вд ;

• •    характеристика рассеивания снарядов по направлению Вб .

Движение снаряда в любой точке траектории описывается системой дифференциальных уравнений. Если положить, что полная аэродинамическая сила определяется наиболее значимой из своих составляющих - силой лобового сопротивления Х а и в любой момент времени направлена противоположно вектору скорости, то систему дифференциальных уравнений движения снаряда можно представить в виде [1]:

' mv = - ^X _a - mg о sin 0 ; mv O = - mg ₀ cos 0 ;

<

- mv cos Oy = 0;

x = v cos O cos y ;

У д = v sin 0 ;

z_g = - v cos O sin y ,

К дифференциальным уравнениям движения снаряда присоединены уравнения математической модели атмосферы:

^тy_g ) = ^T N ⁽ У д )+M Уд );

P 0 = P 0 N +^A p о ;

^{П (}У д ) = —

д 0 N y g

^{R t (} У д )

^{П (} У д );

P ⁽ У д ) = P 0 ^{П (} У д );

Р ⁽ У д ) =

P ⁽ У д ) . ^{R T (} У д )’

a ⁽ У д ) = 7 X ^{R T (}У д ) ;

W = 0;

^ W = 0;

0w = 0, где т (Уд) - нормальный закон изменения виртуальной температуры с высотой:

f 289 - 6,328 - 10 ^{- 3} у„ , если 0 <  у, <  9324 м, gg

Т ( Уд ) = ^ 230 - 6,328 - 10 ^{- 3}( y_g - 9324) + 1,172 - 10 ^{- 6}( y_g - 9324)², если 9324 м <  y_g <  12000 м

221,5, если y_g >  12000 м ,

P_o - давление воздуха у поверхности Земли на уровне моря;

P_OjV - нормальное атмосферное давление воздуха у поверхности Земли на уровне моря;

Ap0  - отклонение давления воздуха от нормального у поверхности Земли на уровне моря;

п(yg)  - функция изменения относительного давления с высотой;

g0N   - ускорение свободного падения Нормальной артиллерийской атмосферы;

R - газовая постоянная сухого воздуха;

p ( y_g ) - функция изменения давления воздуха с высотой;

р ( У₈ ) - функция изменения плотности воздуха с высотой;

a ( y_g ) - функция изменения скорости звука с высотой;

X - показатель адиабаты воздуха;

Система (2) интегрируется при следующих начальных условиях: t=0, v=v o , 0=0 0 , w=V 0 , X g =y g =Z g = 0.

Интегрирование данной системы проводилось с помощью метода Рунге-Кутты 4 порядка, поскольку он является одним из наиболее точных и дает наименьшие погрешности при расчетах. Отличительной чертой данного метода является то, что при вычислении следующей точки x_m+1,y_m+1 используется информация только о точке x_m ,y_m , но не о предыдущих [2].

Для более достоверной оценки рассеивания снарядов при стрельбе было смоделировано 100 теоретических траекторий полета при одних и тех же начальных условиях для каждого орудия. Графики полученных результатов представлены на рисунках 1-6.

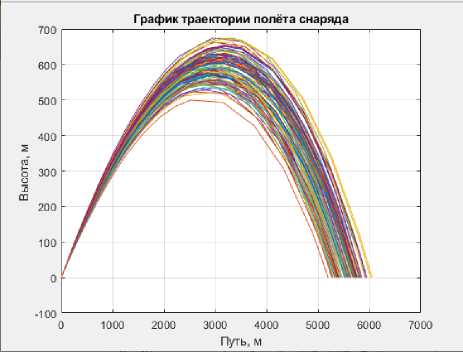
Рисунок 1 - Траектория полета снаряда ЗВОФ68

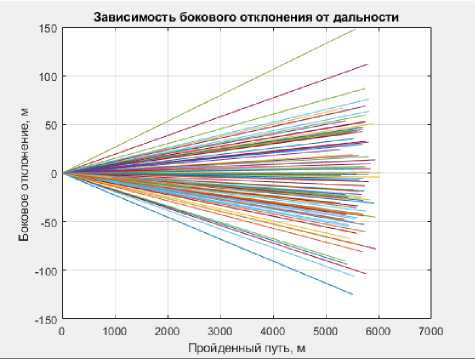
Рисунок 2 – Зависимость бокового отклонения снаряда ЗВОФ68 от дальности

полета

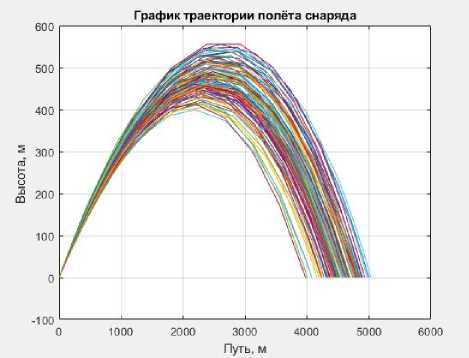
Рисунок 3 - Траектория полета снаряда М933

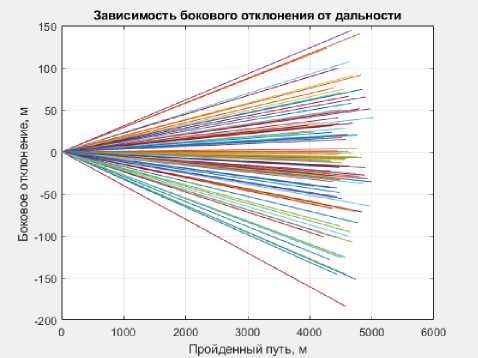
Рисунок 4 – Зависимость бокового отклонения снаряда М933 от дальности

полета

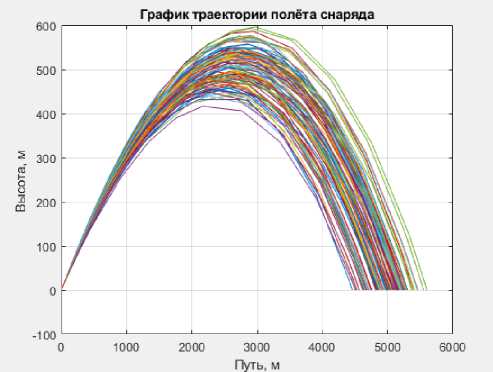
Рисунок 5 - Траектория полета снаряда МО-120-RT-61

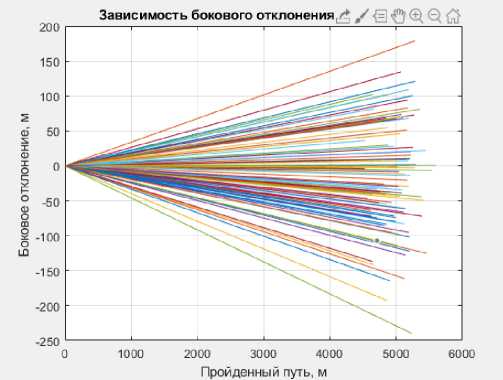
Рисунок 6 – Зависимость бокового отклонения снаряда МО-120-RT-61от дальности полета

С помощью графиков и расчетной программы были получены следующие характеристики эффективности стрельбы для орудия каждой страны:

• 1)    Российский миномет:

• a.    средняя дальность стрельбы – 5623 м;

• b.    Вд = 126 м;

• c.    Вб =33 м.

• 2)    Американский миномет:

• a.    средняя дальность стрельбы – 4505 м;

• b.    Вд = 149 м;

• c.    Вб =45 м.

• 3)    Французский миномет:

• a.    средняя дальность стрельбы – 5030 м;

• b.    Вд = 147 м;

• c.    Вб =52 м.

Исходя из анализа полученных результатов можно придти к выводу, что, при наибольшем значении дальности полета снарядов наименьшие характеристики рассеивания как по дальности, так и по направлению имеет русский миномет «Нона-М1».

Кроме того, следует отметить, что знание характеристик кучности стрельбы необходимо не только баллистикам, составляющим таблицы стрельбы или инженерам, разрабатывающим новое вооружение. Знание данных характеристик приносит пользу и непосредственно артиллеристам, поскольку позволяет понять, сколько снарядов необходимо выпустить по цели, чтобы гарантировать попадание.