Сравнительное исследование геометрических характеристик микрокапилляров для проведения химических реакций

В последние годы значительно возрос интерес к использованию микрокапилляров в химических реакциях [1–2], что связано с их особыми характеристиками, такими как высокий коэффициент теплопередачи и возможность точного контроля процессов на микроуровне. Эти свойства делают микрокапилляры идеальными инструментами для исследований в области химии, фармацевтики и биотехнологий. Развитие микрорадиаторных технологий привело к новым возможностям повышения эффективности химических реакций за счет оптимизации смешивания реагентов на микроскопическом уровне. Одним из ключевых факторов, влияющих на производительность микрокапилляров, является их геометрия, которая определяет динамику потоков и степень смешивания жидкостей.

В данной работе проводится сравнительное исследование геометрических характеристик различных типов микрокапилляров, применяемых в химических реакциях. Основное внимание уделяется влиянию геометрии на эффективность смешивания и взаимодействия реагентов при низких значениях числа Рейнольдса. Этот аспект имеет решающее значение для разработки более эффективных микрореакторов, способных улучшить результаты во множестве областей – от синтеза лекарственных препаратов до производства высококачественных наноматериалов.

Прогресс в микро- и нанотехнологиях также сыграл важную роль в развитии микрокапилляров. Каналы диаметром менее 1 мм обеспечивают значительно более высокий коэффициент теплопередачи по сравнению с традиционными реакционными сосудами, что повышает энергоэффективность процессов и снижает затраты. Малые размеры каналов увеличивают удельную площадь поверхности, способствуя лучшей теплопередаче.

Исследования показывают [1, 3], что для оптимизации теплопередачи и минимизации гидравлического сопротивления необходимо учитывать геометрию микрокапилляров. Форма канала, его диаметр и структура внутренней поверхности оказывают непосредственное влияние на поведение жидкости и газов в микрокапилляре, что, в свою очередь, определяет общую эффективность реакций. Кроме того, вариации в этих параметрах могут привести к значительным изменениям в кинетике химических процессов, что делает их важным фактором при разработке и оптимизации микрореакторов.

Основной реакцией для выявления подходящей геометрии микрокапилляров будет являться альдольная конденсация ацетона [4] в условиях щелочной среды, в результате которой выходит важное промышленное вещество, широко используемое в производстве красок, чернил, лаков, клеящих составов, виниловых смол и сополимеров, а также в синтезе пестицидов и в качестве промежуточного соединения для органического синтеза. Альдольная конденсация ацетона является многоступенчатой реакцией [5–6], в ходе которой из ацетона, воды и щелочного катализатора образуются промежуточные соединения (диацетоновый спирт и мезитилоксид) и побочные продукты (оксилитон и тяжёлые соединения), с получением целевого продукта – изофорона [7]. Коммерческая эффективность этого процесса зависит от контроля над специфичностью реакции и поддержания высокой селективности в рамках стехиометрических соотношений. Одним из ключевых параметров работы установки является селективное использование ацетона в процессе получения 3,5,5-триметил-2-циклогексен-1-она. На селективность оказывают влияние такие факторы, как температура, давление, концентрация реагентов и гидродинамические условия, а применение микрофлюидных технологий может способствовать повышению селективности до 10–15% [8].

Цель работы – сравнительное исследование геометрических характеристик микрокапилляров различных форм для оптимизации проведения химических реакций, а также анализ влияния этих характеристик на такие ключевые параметры, как перепад давления, смешивание и массоперенос в микрофлюидных системах с использованием программы COMSOL Multiphysics.

Материалы и методы

В данном исследовании будут рассматриваться серпантинообразной, фрактальной и лобулярной формы микрокапилляра (рисунок 1) [19–20]. Лобулярная, в дальнейшем «лобуляр», форма микроканалов увеличивает площадь поверхности, улучшает удержание жидкости, снижает гидродинамическое сопротивление и риск запирания потока, а также повышает прочность и устойчивость к механическим нагрузкам. В серпантинообразных, в дальнейшем «серпантин», микрокапиллярах, благодаря многократным изменениям направления потока, удается добиться более равномерного распределения реагентов по всему объему, что важно при проведении экзотермических реакций. Фрактальные, в дальнейшем «фрактал», микрокапилляры представляют собой сочетание извилистых и ветвящихся каналов, что позволяет эффективно управлять потоками на микроуровне и минимизировать потери давления.

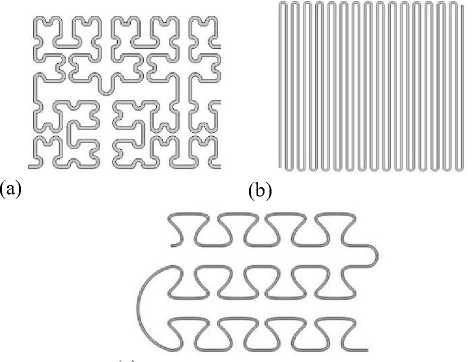
Рисунок 1. Раз(лcи) чные формы микроканалов (a – фрактал, b – серпантин, c – лобуляр)

Figure 1. Different shapes of microchannels (a – fractal, b – serpentine, c – lobular)

Данные формы микроканалов были выбраны за их способность обеспечивать высокую эффективность реакций в условиях низких чисел Рейнольдса, а также за их способность к улучшению теплопередачи и перемешивания. Кроме того, исследование этих геометрий позволило глубже понять, как их особенности влияют на процессы гидродинамики и теплопередачи, что важно для дальнейшего улучшения и оптимизации микрореакторных систем.

Кинетические параметры получения 3,5,5-триметил-2-циклогексен-1-она были получены по справочным данным из работы [9–13], прописанные в таблице 1. В качестве критерия оптимальности потока использовалась средняя молярная концентрация 3,5,5-триметил-2-цик-логексен-1-она на выходе из реакционного микрокапилляра [14–16].

Альдольная конденсация ацетона (1–5) – процесс многостадийный [17–18], включающий следующие реакции:

k 1

2 C3 H6 O ^ C6 H12 O2

^

k 2

k 3

C6 H12 O2 ^ C6 H10 O + H 2 O(2)

^

k 4

k 5

C3 H6 O + C6 H10 O ^ C9 H14 O + H 2 O(3)

^

k 6

k 7

CH14O + CHO ^ CHO + HO(4)

k 8

• 2 CHO ^ CHO + H 2O(5)

Таблица 1.

Кинетические параметры стадий получения 3,5,5-триметил-2-циклогексен-1-она

Table 1.

Kinetic parameters of the steps in the preparation of 3,5,5-trimethyl-2-cyclohexen-1-one

Реакция Reaction	Константа Constant	Предэкспонтенциальный множитель Pre-exponential multiplier	Энергия активации, кДж/кмоль Activation energy, kJ/kmol
1	k1	4,08 x 102, м3ч/кмоль	14650
	k2	3,37 x 109, 1/ч	34400
2	k3	7,19 x 1015, 1/ч	90000
	k4	5,98 x 108, 1/ч	53038
3	k5	3,19 x 1017, м3ч/кмоль	93259
4	k7	5,35 x 102, м3ч/кмоль	34400
5	k8	4,52 x 1014, м3ч/кмоль	90000

Для сравнительной характеристики микрокапилляров различной геометрии будет применялся ряд методов исследования, с использованием программы COMSOL Multiphysics, что обеспечит комплексный анализ и моделирование различных аспектов работы микрокапилляров. Программа COMSOL позволяет интегрировать различные физические процессы и управлять ими в едином программном окружении. В рамках этого исследования использовались следующие методы и уравнения:

Анализ скорости потока и распределения скорости. В COMSOL Multiphysics применялось решение уравнений Навье–Стокса для анализа скорости потока и распределения внутри микрокапилляров. В программе для моделирования потока используется уравнение:

• p(— + v V v ^ = V p + p V ² v + f    (6)

• <5 1        J

где p - плотность жидкости, v - вектор скорости, p - давление, p - динамическая вязкость, f – внешняя сила.

Моделирование реакционно-диффузионных процессов. Уравнение для моделирования реакционно-диффузионных процессов в микроканалах с учетом конвективного переноса, диффузии и химической реакции описывается в интерфейсе

Transport of Diluted Species и выглядит следующим образом:

с„ P vL Pe =

x

ас

— + V ( - D V С + vC ) = R д t      ^v               '

где C – концентрация вещества, D – коэффициент диффузии, v – вектор скорости потока, R – скорость химической реакции.

Моделирование критерия Рейнольдса. Используя встроенные физические интерфейсы для моделирования течения жидкости, можно рассчитать скорость потока, профиль давления и другие параметры, необходимые для вычисления критерия Рейнольдса по формуле:

Re = P d p

где р - плотность жидкости, v - средняя скорость потока, d – гидравлический диаметр микроканала, ^ - динамическая вязкость жидкости.

Моделирование критерия Пекле. Немаловажным параметром является критерий Пекле, характеризующий соотношение между конвективными и молекулярными процессами переноса теплоты. Данный критерий можно также задать в программе и рассчитать по формуле:

где с – удельная теплоемкость при постоянном давлении, р - плотность жидкости, v - скорость потока жидкости относительно поверхности теплообмена, L – характерный линейный размер поверхности теплообмена, x – коэффициент теплопроводности жидкости

Результаты и обсуждения

0D моделирование . Для корректного моделирования в программной среде COMSOL сначала необходимо провести верификацию кинетических расчётов в 0D. Для этого был использован модуль «Reaction Engineering» COMSOL, основанный на стандартных уравнениях для расчёта кинетических параметров. Входными данными служили концентрации: 0,010324 моль/л ацетона и 0,0135 моль/л воды. На рисунке 2 (a) показано распределение концентраций ацетона и воды, полученных в результате моделирования на основе кинетических параметров реакции. Также данный модуль позволяет визуализировать кинетические кривые концентраций изофорона и основных побочных продуктов (рисунок 2 (b)).

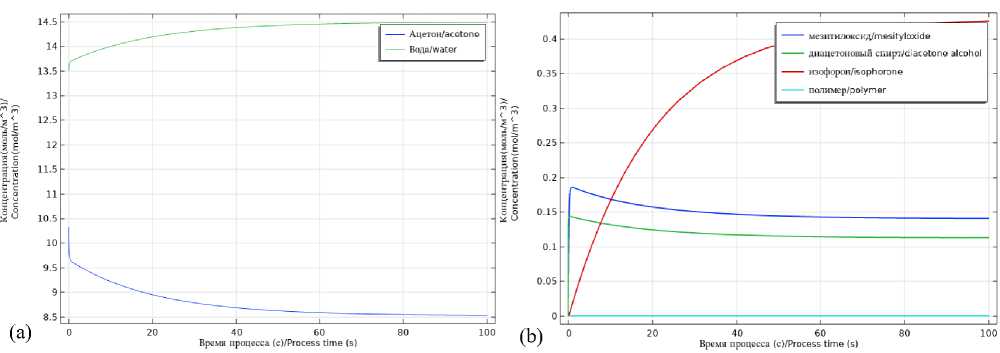
Рисунок 2. Кинетические кривые компонентов (a – исходные вещества, b – изофорон и основные побочные продукты)

Figure 2. Kinetic curves of components (a – starting substances, b – isophorone and main by-products)

2D моделирование . Для определения наиболее эффективной геометрии необходимо, чтобы площадь каналов была неизменной, и она равна ~ 20 см². На входе также задавался и в последующем варьировался объемный расход исходных компонентов. Исходным значением является 0,25 мл/мин по ацетону и воде. Варьировался параметр от исходного значения до 2 мл/мин с шагом 0,25 мл/мин. Концентрации данных веществ совпадают с заданными при 0D моделировании.

По окончании расчетов были выведены графики зависимостей различных параметров друг от друга. Так, при изучении зависимости концентрации изофорона на выход от расхода поступающих реагентов (рисунок 3) видно, что при геометрии «фрактал» достигается максимальный выход продукта ~ 2%.

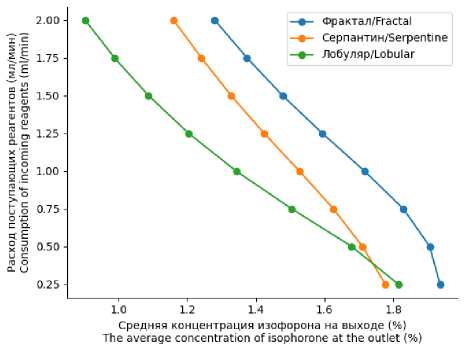
Рисунок 3. Зависимость средней концентрации изофорона на выходе от расхода поступающих реагентов Figure 3. Dependence of average isophorone concentration at the outlet on the flow rate of incoming reagents

В системе необходимо поддерживать оптимальный перепад давления, чтобы не возникало рисков, снижения энергоэффективности и затруднения контроля над важными параметрами, что может негативно сказываться на эффективности процессов. Рассматривая рисунок 4, видно, что при геометрии «фрактал» возникает больший перепад давления, чем при системе «лобуляр».

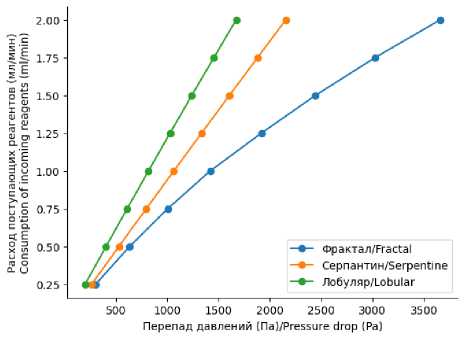
Рисунок 4. Зависимость перепада давления от расхода поступающих реагентов

Figure 4. Dependence of pressure drop on the flow rate of incoming reagents

На рисунке 5 представлена зависимость перепада давления от числа Рейнольдса для трех геометрий микроканалов. Геометрия «фрактал» демонстрирует наибольший перепад давления, достигая более 3500 Па при Re ~ 60, что связано с высокой сопротивляемостью потоку из-за сложной траектории. «Серпантин» показывает более умеренный рост давления (около 2500 Па при тех же условиях), обеспечивая лучшее соотношение сопротивления и контроля потока. Наименьший перепад давления наблюдается для формы «лобуляр», где при Re = 60 перепад давления составляет около 1500 Па. Это делает геометрию грибы оптимальной для минимизации гидравлических потерь и энергозатрат в системе микроканалов.

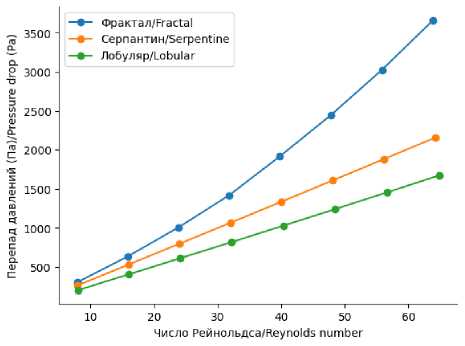
Рисунок 5. Зависимость критерия Рейнольдса от перепада давления в системе микрокапилляров

Figure 5. Dependence of the Reynolds criterion on the pressure drop in the microcapillary system

В микроканалах необходимо поддерживать доминирование конвективного переноса над молекулярной диффузией, что характеризуется числом Пекле [10]. На рисунке 6 видно, что концентрация 3,5,5-триметил-2-циклогексен-1-она на выходе уменьшается с увеличением числа Пекле для всех трех геометрий, что свидетельствует о лучшем перемешивании в системе. Геометрия «лобуляр» демонстрирует наибольший эффект уменьшения концентрации при увеличении числа Пекле, что говорит о более интенсивном перемешивании и лучшей диффузии. Наименьшее снижение концентрации наблюдается у геометрии «фрактал», что связано с более низкой эффективностью перемешивания в такой форме.

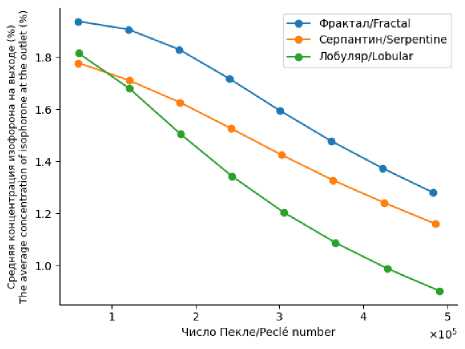
Рисунок 6. Зависимость числа Пекле от средней концентрации изофорона на выходе

Figure 6. Dependence of the Peclet number on the average isophoron concentration at the outlet

С ростом числа Рейнольдса также наблюдается снижение концентрации изофорона для всех геометрий (рисунок 7). Однако, как и в случае с числом Пекле, наибольшее снижение демонстрирует геометрия грибы, что указывает на ее преимущество в интенсификации массо-обмена и перемешивания при более высоких скоростях потока.

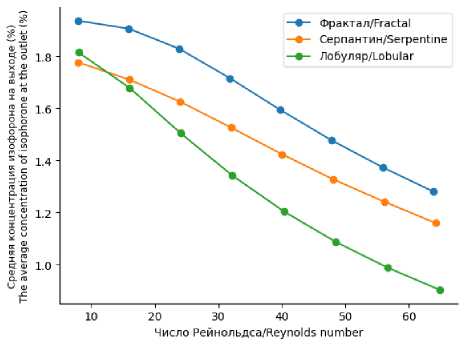
Рисунок 7. Зависимость числа Рейнольдса от средней концентрации изофорона на выходе

Figure 7. Reynolds number dependence on the average isophoron concentration at the outlet

Заключение

В результате проведенного сравнительного исследования геометрических характеристик микрокапилляров для проведения химических реакций были получены данные о влиянии формы микроканалов на основные параметры, такие как перепад давления, эффективность перемешивания и транспортные свойства.

Геометрия микроканалов значительно влияет на перепад давления и эффективность смешивания. Микроканал типа "фрактал" показал наибольший перепад давления при всех значениях числа Рейнольдса, что связано с его сложной траекторией. С другой стороны, форма «лобуляр» показала минимальные гидравлические потери, что делает её предпочтительной для снижения энергозатрат в микросистемах. Анализ числа Пекле показал, что геометрия «лобуляр» обеспечивает наилучшее перемешивание за счет эффективного конвективного переноса, особенно при высоких значениях числа Пекле. Это подтверждает ее преимущество в задачах, где важен интенсивный массоперенос. При увеличении числа Рейнольдса, наблюдалось улучшение смешивания во всех геометриях. Однако микроканал «лобуляр» показали наиболее резкое снижение концентрации изофорона на выходе, что свидетельствует о лучшем перемешивании даже при относительно небольших затратах энергии. Перепады давления в микроканалах должны оставаться в пределах, позволяющих поддерживать оптимальный режим течения без чрезмерного увеличения энергетических затрат. Геометрия «лобуляр» в этом аспекте снова показала наилучшие результаты, обеспечивая минимальные потери давления при сохранении высокой эффективности перемешивания.

Таким образом, можно заключить, что геометрия микроканалов играет ключевую роль в оптимизации рабочих параметров микрофлю-идных систем. Форма «лобуляр» представляется наилучшей в условиях, где критичны минимизация гидравлических потерь и максимальная эффективность перемешивания.