Сравнительный анализ методов фильтрации шума при низкотемпературном воздействии на биоткани

DOI:

Решая практически все научные или технические проблемы, приходится сталкиваться с обработкой различных сигналов. Информация, записанная в виде сигналов, может храниться, передаваться, обрабатываться как в виде непрерывных функций, а также и в цифровой форме. Однако в настоящее время предпочтение отдается цифровым методам обработки сигналов с использованием компьютерных технологий. Методы цифровой обработки сигналов занимают очень важное место в решении широкого класса задач в различных областях науки и техники. Эти методы в настоящее время являются активно развивающейся областью информационных технологий [1; 5; 6; 8]. Обнаружение и извлечение значимой информации из записанного сигнала, фильтрация шума и улучшение качества сигнала, а также восполнение недостающих данных во многих случаях являются одними из основных целей обработки сигнала.

На качество сигналов существенно влияет шум различного происхождения. Фильтрация шума выполняется во временной или частотной области, в зависимости от решаемой проблемы. Для этого обычно считается, что существует довольно значительная разница в спектральных характеристиках сигналов и шума. Классические алгоритмы фильтрации сигналов в частотной области обычно основаны на использовании различных интегральных преобразований сигналов, в частности на преобразовании Фурье [6–8].

Низкотемпературное воздействие на биоткани неизбежно сопровождается различными видами шума. При воздействии на биоткань низкими температурами регистрируемый сигнал датчиками может быть искажен шумом, который вызван различными факторами: технический шум (шум датчиков, электронных цепей), биологический шум (колебания биологических процессов в ткани), внешние факторы (движение пациента, вибрации, электромагнитные помехи).

Для устранения искажений, фильтрации шумов в настоящее время используется достаточно широкий набор алгоритмов [6; 7]. Однако данные алгоритмы не дают оценку качества сглаживания. Получается, что главная проблема всех методов – отсутствие критерия оценки качества сглаживания.

В работах Ю. Каламбет, С. Мальцева, Ю. Козьмина [7; 8] авторы предлагают алгоритм цифровой фильтрации. Данный алгоритм основан на минимизации доверительного интервала аппроксимации. В статье приводятся примеры для обработки. Данные примеры позволяют согласиться с утверждением, что «предложенный алгоритм ставит точку в дискуссии о том, какой метод фильтрации шумов лучше». В работах [7; 8] авторами также предложена технология сравнения и отбора методов сглаживания в применении к определенным задачам. Сравнительная оценка была проведена с использованием различных методов сглаживания: медианное сглаживание, скользящее среднее, адаптивное сглаживание и т. д.

В работе [5] приведены результаты исследований по уменьшению и устранению шума на снимках с использованием методов фильтрации.

Цель настоящей работы – провести сравнительный анализ методов фильтрации шума, возникающих при низкотемпературном воздействии на биоткани.

В данной работе предложены методы фильтрации шума: медианное сглаживание, скользящее среднее, фильтр Калмана, метод наименьших квадратов. Данные для обработки, полученные в процессе решения задачи с фазовыми переходами, описывают тепловой процесс низкотемпературного воздействия на биологической ткани.

Полученные в настоящей работе результаты можно применить для повышения точности диагностики и лечения в здравоохранении, а также расширения возможности биологических исследований.

1. Постановка задачи

При деструкции биологических тканей в различных областях медицины применяются достаточно протяженные плоские аппликаторы [2–4; 15; 17; 19; 20]. Определение динамики температурного поля в этом случае сводится к решению следующей задачи со свободными границами для нелинейных эволюционных уравнений [9; 10; 14; 18]:

0

—--Hu = —H ^(t), x = 0, dx

u(_S(t),t) = 0,  " ''/"

u(0,ti) = 1;

ti 2: u_xx—_-2 — =0, 0 R 4

uxx — dt = ue, x (t)

—--Hu = —H ^(t), x = 0, dx

Mx* = ⁰,

= Px*_t, u(x* (t),t) = 1, x*

u(s(t),t) = 0, " \'/    "

u(0,t2) = u_n;

t >t2: uxx — dt = ue,  x * *(t)

—--Hu = —H уН), x = 0, dx

M_x** =^0,    1^1    = ^Pxt*, ^u(x**^(t),t) = ¹

Ldxj _x**

u(s(t),t) = 0,   ^&u(S^^,t) =0,

^[u]x* = ⁰ [lx]   = ^Px* ^u(x*^(t),t) = ¹

В (1)-(3) требуется определить температурное поле u = u(x,t) и границы x** = = x**(t), x* = x*(t), s = s(t). Остальные величины (1)-(3) a, H, P, P1 - известные параметры, u₀(x), cp(t) — известные функции, a 6 в < 1, a²= ||p, H = a^1,

w = aw₀, w₀= Ckm_k, a =

[T - (T - T*)] 1 в, ф = 1 + |uA(t) - |, uA(t) = ua (1 - e-2), ua = Ы*, P = = (T -T*), P = Лр, un = И**, T = 36,7°C, T* = 0 ± 3°C, T** = 0 ± 30 °C, TA — температура аппликатора, Л, с, р, Л — теплофизические харак теристики биологической ткани, ck, mk — теплоемкость и скорость массы крови; в — параметр нелинейности; знак черты относится к незамороженной, снизу к замороженной области биологической ткани, [ 5 означает скачок стоящей под ним функции.

В начальный период времени происходит только охлаждение биологической ткани. Динамика процесса охлаждения описывается решением задачи со свободной границей [9; 10; 14; 18]:

u_xx - dt = и^в,  0 0 < t < ti,

u(x, 0) = u0(x), 0 < x < s(0),   (s(0) = 0), du

—--h(u -uA(t)), x = 0, 0 < t < t1, dx

u(s(t),t) = 0,   ^du(^^),t) =0, 0 i,

u(0, t1) = 1.

Разработаны программные комплексы для ЭВМ «Плоско-параллельная гипотермия и криодеструкция биологической ткани в медицине» [12], «Компьютерное моделирование низкотемпературного воздействия на биологические ткани в криохирургии» [11]. Каждый комплекс состоит из программ: программа 1 определяет максимальный размер замораживания, температуру биологической ткани в начале процесса охлаждения методом Ньютона – Рафсона, динамику температурного поля; программа 2 строит график динамики температурного поля.

В предлагаемой работе требуется определить температуру криозонда для низкотемпературного воздействия на биологические ткани, которая не навредит биоткани, причем температуру необходимо определить максимально точно.

2.    Источники шума и методы их фильтрации при низкотемпературном воздействии на биоткани

При низкотемпературном воздействии на биологическую ткань шумы могут возникнуть от различных источников. И прежде чем рассматривать методы фильтрации шума, приведем в данной работе некоторые основные источники шума.

Одним из источников шума являются температурные флуктуации: микроскопические колебания температуры в тканях, обусловленные тепловым движением молекул. Причиной шума могут быть погрешности сенсоров, связанные с ограниченной точностью и чувствительностью датчиков температуры, теплового потока и других параметров. Шумы могут быть связаны с шумом оборудования: шум, генерируемый криогенным оборудованием (насосы, компрессоры, системы управления). Биологическая изменчивость тоже является источником шума. Данный шум связан с неоднородностью и изменчивостью биологических тканей.

Различные методы фильтрации шума могут быть применены к данным при низкотемпературном воздействии. Наиболее распространены из них: скользящее среднее, медианный фильтр, фильтр Калмана, вейвлет-преобразование, методы машинного обучения и др. [6; 7; 13].

Скользящее среднее (Moving Average) является одним из простых и эффективных методов для сглаживания данных путем усреднения значений в скользящем окне. Данный метод может размывать резкие изменения, и эффективен для устранения высокочастотного шума.

Медианный фильтр, как пишут авторы работы [16], используется в цифровой обработке сигналов и изображений для снижения уровня шума. Согласно методу медианного фильтра каждое значение заменяется медианой значений по соседству, обработанные выборки в окне фильтра сначала сортируются по возрастанию или убыванию. А значение в середине отсортированного списка отправляется на вывод фильтра. Если объем данных четный, то выходное значение фильтра равно среднему значению двух выборок в середине упорядоченного списка [16]. Этот метод по сравнению с другими методами фильтрации более устойчив к выбросам, чем метод скользящей средней.

Фильтр Калмана является итеративным алгоритмом для оценки состояния системы на основе шумных измерений. Может эффективно фильтровать шум при наличии динамической модели процесса.

Вейвлет-преобразование (Wavelet Transform) позволяет разложить сигнал на различные частотные компоненты и отфильтровать шум на основе анализа вейвлет-коэф-фициентов. Данный метод хорошо подходит для обработки нестационарных сигналов и сохранения локальных особенностей.

Методы машинного обучения (методы, основанные на обучении с учителем и без учителя) могут быть использованы для обучения модели, способны определять шум от полезного сигнала. Выбор оптимального способа фильтрации зависит от типа шума, характеристик сигнала, доступных вычислительных ресурсов и целей исследования. Для простого сглаживания и удаления высокочастотного шума могут быть использованы скользящее среднее или медианный фильтр. Для более точной фильтрации, когда требуется сохранить детали и локальные особенности, лучше использовать фильтр Гаусса или вейвлет-преобразование. Если имеется динамическая модель процесса, то фильтр Калмана может быть очень эффективным. Методы машинного обучения могут быть применены для фильтрации сложного и нерегулярного шума, но требуют значительного объема данных и вычислительных ресурсов.

3.    Скользящее среднее для фильтрации шума

Среднее значение фильтрации шума в стационарном временном ряду определяется как математическое ожидание любого единичного значения [8; 16]. Как пишут авторы работ [8; 16], это связано с его стационарностью и математическим ожиданием, которое не зависит от времени наблюдения. В качестве оценки среднего значения в данном методе используется среднее значение выборки значений ряда, определяемое как сумма значений ряда, деленная на их общее количество. Проведены расчеты программным комплексом и найдены значения температуры x_k.

Сначала создается новый набор средних арифметических значений, рассчитывае- мых для временных интервалов длиной q:

q+k

Е ^х(^ х(к) = =----, к =1,2,...,п — q + 1,

q где q означает длину периода сглаживания, к — порядковый номер среднего значения. Выбор продолжительности периода сглаживания зависит от типа временного ряда, а также и от цели сглаживания. Выбор делается исследователем. Простое сглаживание основано на этой серии [16].

При применении скользящей средней в 2к + 1 данных вычисляется среднее значение, которое считается сглаженным значением в средней точке к + 1. Это означает, что вес каждой точки равен 1 / (2к + 1). Сжатие данных, при котором среднее значение берется вместо нескольких последовательных точек, является частным случаем скользящего среднего. Чрезмерная частота использования этого метода не повышает точность анализа. При этом увеличивается время обработки данных и объем памяти. Когда данные сжимаются, то постоянная времени увеличивается в п раз, а количество шума уменьшается примерно в п раз. Вместо простого среднего исследователи часто используют средневзвешенное значение [16].

Составлены новые ряды для температуры из простых средних арифметических значений, для промежутков длиной 2, 3, 4, 5 (см. табл. 1). Проведя сравнительный анализ, можем утверждать, что чем промежуток больше, тем возникает больше шума.

4.    Медиа´нный фи´ льтр как метод оптимизации шума

Медиана временного ряда, используемого в срединном фильтре, определяется как медиана распределения реализаций случайной функции в момент времени t. Это означает, что медиана — это действительное число, вероятность превышения которого для любого измерения равна 0,5. Для стационарного временного ряда это значение не зависит от времени наблюдения [8; 16].

Этот метод основан на вычислении скользящей медианы. Чтобы найти значение скользящей медианы в точке t, сначала вычисляется медиана значений ряда во временном интервале [t — q, t + q]. Основным преимуществом использования данного метода для фильтрации шума является его устойчивость к выбросам [6–8; 16].

По данному алгоритму, как пишут авторы работ [6–8; 16], для моментов времени t, отстоящих от начала или конца ряда менее чем на q точек, вычисление медиан становится невозможным. Чтобы не сужать область определения сглаженного ряда по сравнению с исходным рядом, используется метод устранения краевых эффектов, согласно которому в качестве сглаженного значения для х(0), где 0 — начальный момент времени, предлагается взять медиану трех точек: х(0), х(1) и 3х(1) — 2х(2). Для последнего момента времени х(п) можно использовать ту же аналогичную формулу.

Для оценки медианы выборки серии используется среднее значение. Это означает, что используется центральный член или половинная сумма центральных членов измерительной последовательности. Предполагается, что выборочная последовательность предварительно упорядочена по возрастанию [8; 16]. Полусумма центральных членов составляет 32,31. Погрешность при применении медианного фильтра носит неустойчивый характер, что не совсем подходит для низкотемпературного воздействия на живые биологические ткани.

5.    Фильтр Калмана для оптимальной фильтрации шума

Фильтр Калмана является онлайн-фильтром. Метод фильтрации Калмана фокусируется на фильтрации значения в последней по времени из измеренных точек. Этот метод используется, когда новое значение формируется из предыдущего результата фильтрации. Отфильтрованное значение — это взвешенная сумма последнего измеренного значения и предыдущего сглаженного значения. Если коэффициенты в методе постоянны, то метод называется экспоненциальным сглаживанием. В общем, фильтр Калма-на создает своего рода модель самонастройки для изменяющихся состояний системы. Сглаживание выполняется на их основе. Фильтр Калмана может быть линейным или нелинейным [6–8; 16], что зависит от решаемой проблемы и обрабатываемых данных.

Таблица 1

Расчеты с использованием метода скользящей средней для фильтрации шума (Calculations using the moving average method for noise filtering)

	Промежуток длины 2		Промежуток длины 3		Промежуток длины 4		Промежуток длины 5
x(k)	Ср. знач.	Погр.	Ср. знач.	Погр.	Ср. знач.	Погр.	Ср. знач.	Погр.
35,98	35,825	0,155	35,67	0,31	35,5175	0,4625	35,366	0,614
35,67	35,515	0,155	35,36333	0,306667	35,2125	0,4575	35,062	0,608
35,36	35,21	0,15	35,06	0,3	34,91	0,45	34,762	0,598
35,06	34,91	0,15	34,76	0,3	34,6125	0,4475	34,468	0,592
34,76	34,61	0,15	34,46333	0,296667	34,32	0,44	34,232	0,528
34,46	34,315	0,145	34,17333	0,286667	34,1	0,36	33,94	0,52
34,17	34,03	0,14	33,98	0,19	33,81	0,36	33,65	0,52
33,89	33,885	0,005	33,69	0,2	33,52	0,37	33,362	0,528
33,88	33,59	0,29	33,39667	0,483333	33,23	0,65	33,074	0,806
33,3	33,155	0,145	33,01333	0,286667	32,8725	0,4275	32,732	0,568
33,01	32,87	0,14	32,73	0,28	32,59	0,42	32,45	0,56
32,73	32,59	0,14	32,45	0,28	32,31	0,42	32,172	0,558
32,45	32,31	0,14	32,17	0,28	32,0325	0,4175	31,896	0,554
32,17	32,03	0,14	31,89333	0,276667	31,7575	0,4125	31,622	0,548
31,89	31,755	0,135	31,62	0,27	31,485	0,405	31,35	0,54
31,62	31,485	0,135	31,35	0,27	31,215	0,405	30,756	0,864
31,35	31,215	0,135	31,08	0,27	30,54	0,81	30,54	0,81
31,08	30,945	0,135	30,27	0,81	30,3375	0,7425	30,326	0,754
30,81	29,865	0,945	30,09	0,72	30,1375	0,6725	30,114	0,696
28,92	29,73	0,81	29,91333	0,993333	29,94	1,02	29,904	0,984
30,54	30,41	0,13	30,28	0,26	30,15	0,39	30,02	0,52
30,28	30,15	0,13	30,02	0,26	29,89	0,39	29,762	0,518
30,02	29,89	0,13	29,76	0,26	29,6325	0,3875
29,76	29,63	0,13	29,50333	0,256667
29,5	29,375	0,125
29,25

Применяя программный комплекс [3;4], найдены значения температуры X_k, но полученные результаты могут иметь небольшие погрешности, поэтому вместо значения x_k получаем:

Vk = Xk + ek.                                     (5)

В (5) e_k — ошибка программы, то есть случайная величина. Из неточных показаний мы должны получить значение X_k,_o, максимально близкое температуре, которая будет безопасна для биоткани.

Пусть мы знаем управляющее воздействие s_k. В качестве управляющего воздействия могут быть: температура инструмента, скорость охлаждения, время воздействия на биоткань и другие параметры, используемые при воздействии на биоткань. Тогда, зная значение на к-м шаге, мы можем получить значение на (к + 1)-м шаге:

Xk+1 = Xk + Sk.

В реальности не имеется возможности учесть все внешние факторы, влияющие на биоткань при низкотемпературном воздействии, поэтому (6) принимает вид:

Xk+1 = Xk + Sk + nk, где nk — ошибка, вызванная внешним воздействием, самой биотканью и т. д.

Это означает, что на (к + 1)-м шаге имеем неточное показание у, неточно рассчитанное значение X_k+1, полученное из значения X_k,_o на предыдущем шаге:

Xk+1 = Xk,o + Sk.

Для фильтрации применим фильтр Калмана, идея которого заключается в том, чтобы из двух неточных значений, взяв их с разными весовыми коэффициентами, получить точную оценку искомого значения.

Определяемая температура тогда определяется по формуле:

Xk+i,o = Kk+iyk+i + (1 — Kk+i) Xk+1.

Путем математических вычислений можно получить формулу для расчета коэффициента Калмана. С ростом к коэффициент Калмана всегда стремится к определенному значению K:

Xk+i,o = KVk+i + (1 — K) Xk+i.

где Xk+i = Xk.

Если предположить, что не знаем управляющее воздействие на биоткань s_k, тогда формула упрощается и имеет вид:

Xk+1,0 = Kyk+i + (1 — K) Xk+i,o.

В случае, когда датчик очень точный, то весовой коэффициент K должен быть близок к единице. В противном случае, K должен быть ближе к нулю.

В таблице 2 X(k) — вычисленные значения температуры с применением программного комплекса [10], e(k) — возможная ошибка программы, s(k) — управляющее воздействие s_k, n(k) — ошибка, вызванная внешним воздействием, самой биотканью и т. д., X(k, 0) — максимально близкое температуре, которая будет безопасна для биоткани, X(k + 1) — значение температуры в следующий момент времени, X(k + 1, 0) —

Фильтр Калмана (Kalman filter)

Таблица 2

ST ST ^ sr ^ -S' + + ^ + $ % 35,98 0,02 0 0,21 35,98 36 36 36 36,02 0,50 0,49 0 36 35,67 0,33 10 0,30 36,30 36 36,32 10 36,30 35,36 0,36 20 0,61 36,34 35,73 36,09 20 36,34 35,06 0,06 30 0,91 36,04 35,12 35,18 30 36,04 34,76 0,24 40 1,21 36,21 35 35,23 40 36,21 34,46 0,46 50 1,51 36,44 34,93 35,39 50 36,44 34,17 0,17 60 1,80 36,14 34,34 34,51 60 36,14 33,89 0,12 70 2,09 36,09 34 34,12 70 36,09 33,88 0,12 80 2,09 36,09 34 34,12 80 36,09 33,30 0,30 90 2,68 36,27 33,60 33,90 90 36,27 33,01 0,01 100 2,96 35,99 33,02 33,04 100 35,99 32,73 0,27 110 3,24 36,24 33 33,26 110 36,24 32,45 0,45 120 3,52 36,42 32,90 33,35 120 36,42 32,17 0,17 130 3,80 36,14 32,34 32,51 130 36,14 31,89 0,10 140 4,08 36,08 32,00 32,10 140 36,08 31,62 0,38 150 4,35 36,35 32 32,37 150 36,35 31,35 0,35 160 4,62 36,32 31,69 32,04 160 36,32 31,08 0,08 170 4,89 36,05 31,15 31,23 170 36,05 30,81 0,19 180 5,16 36,16 31 31,18 180 36,16 28,92 0,08 190 7,05 36,05 29 29,07 190 36,05 30,54 0,45 200 5,43 36,43 31 31,45 200 36,43 30,28 0,28 210 5,69 36,26 30,56 30,85 210 36,26 30,02 0,02 220 5,95 36,00 30,04 30,06 220 36,00 29,76 0,23 230 6,21 36,21 30 30,23 230 36,21 29,50 0,49 240 6,47 36,47 30 30,49 240 36,47 29,25 0,25 250 6,72 36,23 29,50 29,75 250 36,23 максимально близкое температуре, которая будет безопасна для биоткани в следующий момент времени, у(к) — неточное показание, рассчитанное по формуле (5), у(к + 1) — неточное показание на к + 1-м слое, К — коэффициент Калмана, t(k) — время воздействия на биоткань, у* — оптимальное показание, полученное с применением фильтра Калмана, к = 0,..., 25.

Результаты расчета показали, что коэффициент Калмана равен 0,500003 (табл. 2). Это означает, что датчик не совсем точный, но не совсем плохой.

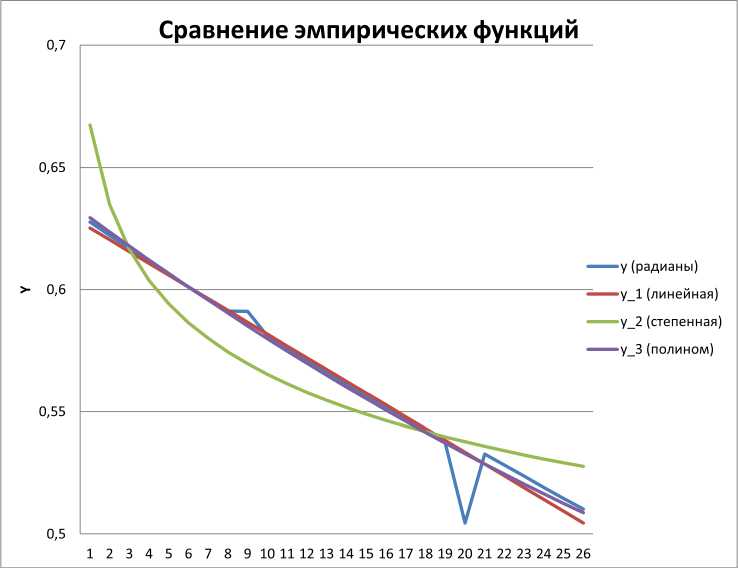
6.    Методы машинного обучения

В статистике понятие линейной регрессии играет очень важную роль, которую применим теперь для анализа данных. Одним из самых популярных алгоритмов для моделей машинного обучения является метод наименьших квадратов (МНК). Наименьшие квадраты – один из вариантов его реализации. Линейная регрессия позволяет решить проблемы подгонки прямой линии, проходящей через ряд точек. Он используется для отбора данных в машинном обучении, а сам метод наименьших квадратов используется для минимизации ошибок путем создания метрики ошибок [16].

Данные для определения погрешностей приведены в следующей таблице (табл. 3).

Таблица 3

Исходные данные (Initial data)

х	у (градусы)	у (радианы)
0,01	35,98	0,62765
0,02	35,67	0,62224
0,03	35,36	0,61684
0,04	35,06	0,6116
0,05	34,76	0,60637
0,06	34,46	0,60114
0,07	34,17	0,59608
0,08	33,89	0,59119
0,09	33,88	0,59102
0,1	33,3	0,5809
0,11	33,01	0,57584
0,12	32,73	0,57096
0,13	32,45	0,56607
0,14	32,17	0,56119
0,15	31,89	0,5563
0,16	31,62	0,55159
0,17	31,35	0,54688
0,18	31,08	0,54217
0,19	30,81	0,53746
0,2	28,92	0,50449
0,21	30,54	0,53275
0,22	30,28	0,52822
0,23	30,02	0,52368
0,24	29,76	0,51915
0,25	29,5	0,51461
0,26	29,25	0,51025

Используя метод наименьших квадратов, аппроксимируем эти данные линейной зависимостью у = ах+Ъ, степенной зависимостью у = ах^ь и квадратичной зависимостью у = ах² + Ъх + с.

Для линейной зависимости значения коэффициентов а и Ъ по методу наименьших квадратов находим из системы уравнений

F а^х2 + Ъ^х_{ = ^2х_{у_{, [   а^Хг + Ъп = ^уг.

В результате получается:

У1 = -0,4826! + 0,63.

Для аппроксимации данных степенной зависимостью произведем замену переменных X = ln(i), У = ln(y) и составим таблицу экспериментальных данных в новых переменных (X, У) (табл. 4).

Таблица 4

Исходные данные в новых переменных

(Initial data in new variables)

X = ln(x)	У = in(y)
-2	-0,20228
-1,69897	-0,20604
-1,52288	-0,20983
-1,39794	-0,21353
-1,30103	-0,21726
-1,22185	-0,22102
-1,1549	-0,2247
-1,09691	-0,22827
-1,04576	-0,2284
-1	-0,2359
-0,95861	-0,2397
-0,92082	-0,24339
-0,88606	-0,24713
-0,85387	-0,25089
-0,82391	-0,25469
-0,79588	-0,25838
-0,76955	-0,26211
-0,74473	-0,26586
-0,72125	-0,26965
-0,69897	-0,29715
-0,67778	-0,27348
-0,65758	-0,27719
-0,63827	-0,28093
-0,61979	-0,28471
-0,60206	-0,28852
-0,58503	-0,29222

Найдем значения коэффициентов а и b по методу наименьших квадратов из системы уравнений

Г а £ X,²+ b £ X, = £ X,y,

\   а ^£X, + bn = ^£У,.

Составим расчетную таблицу (см. табл. 5).

В результате получается

У2 = 0,4789х^-0’⁰⁷².

Таблица 5

Расчетная таблица (Calculation table)

X = ln(x)	У = ln(y)	X 2	ХУ
-2	-0,20228	4	0,4046
-1,69897	-0,20604	2,886499	0,3501
-1,52288	-0,20983	2,31916	0,3195
-1,39794	-0,21353	1,954236	0,2985
-1,30103	-0,21726	1,692679	0,2823
-1,22185	-0,22103	1,492914	0,2701
-1,1549	-0,2247	1,333799	0,2595
-1,09691	-0,22827	1,203212	0,2503
-1,04576	-0,2284	1,093609	0,2388
-1	-0,2359	1	0,2359
-0,95861	-0,2397	0,918928	0,2298
-0,92082	-0,2434	0,847907	0,2241
-0,88606	-0,24713	0,785096	0,2189
-0,85387	-0,25089	0,729097	0,2142
-0,82391	-0,25469	0,678826	0,2098
-0,79588	-0,25838	0,633425	0,2056
-0,76955	-0,26211	0,592209	0,2017
-0,74473	-0,26586	0,554619	0,1979
-0,72125	-0,26965	0,520196	0,1944
-0,69897	-0,29714	0,488559	0,2076
-0,67778	-0,27347	0,459387	0,1853
-0,65758	-0,27719	0,432408	0,1823
-0,63827	-0,28093	0,407391	0,17931
-0,61979	-0,28471	0,384138	0,1764
-0,60206	-0,28852	0,362476	0,1737
-0,58503	-0,29222	0,342256	0,1709

Значения коэффициентов а, Ь, с при аппроксимации квадратичной зависимостью по методу наименьших квадратов находим из системы уравнений

' а Е -4 + Ь Е -3 + с £ -2 = Е ^у*, < аЕ-3 + Ь^х²+ сЕ-* = Е^ж^’ аЕ^Xi + ЬЕ^Xi + с^п = ЕУ*'

В результате их выравнивания получена функция

У3 = 0,4192х²- 0,5958х + 0,6353.

Далее находим отклонения и суммы квадратов отклонений.

Суммы квадратов отклонений получаются 0,001028, 0,005958, 0,000913 соответственно.

Выясним, какая из трех линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Для этого сравниваем суммы квадратов. Очевидно, что 0,000912868 меньше, чем остальные значения, а это означает, что третья линия лучше в смысле метода наименьших квадратов выравнивает данные (см. рис. 1).

7.    Сравнительный анализ методов фильтрации

Проведем сравнительный анализ использованных методов фильтрации шума. Анализ проведем по эффективности, по ограничениям, по вычислительным затратам, по применению данных методов для фильтрации шума.

В методах, основанных на скользящем средневзвешенном значении, возможно сглаживание по четному числу точек. В большинстве случаев результат для средневзвешенного значения соответствует центру массива данных, то есть абсцисса с симметричным окном 2к попадает в середину между к-й и k + 1 точками битовой сетки. Поскольку задача фильтрации шума обычно не включает смещение разрядной сетки, на практике этот вариант сглаживания используется редко. Массив обрабатываемых исходных данных должен быть больше, чем окно фильтра. Методы, основанные на скользящем средневзвешенном значении с окном 2к + 1, не могут рассчитать приблизительное значение в первой и последней к точках массива данных, поэтому для оценки значений в этих точках необходимо использовать дополнительные условия [8; 16].

Таблица 6

Квадрат отклонений (Square of deviations)

(у - У1)2	(у - У2)2	(У - Уз)2
0,000006	0,001563	0,000003
0,000004	0,000155	0,000002
0,000002	0,000000	0,000001
0,000001	0,000061	0,000000
0,000000	0,000149	0,000000
0,000000	0,000216	0,000000
0,000000	0,000260	0,000000
0,000000	0,000282	0,000001
0,000020	0,000461	0,000035
0,000001	0,000245	0,000001
0,000001	0,000209	0,000001
0,000001	0,000171	0,000001
0,000001	0,000130	0,000001
0,000002	0,000090	0,000001
0,000002	0,000053	0,000001
0,000001	0,000026	0,000001
0,000001	0,000008	0,000001
0,000001	0,000000	0,000000
0,000001	0,000005	0,000000
0,000840	0,001105	0,000807
0,000017	0,000010	0,000017
0,000019	0,000034	0,000014
0,000022	0,000075	0,000011
0,000025	0,000134	0,000007
0,000028	0,000212	0,000004
0,000033	0,000304	0,000002

Рис. 1. Сравнение эмпирических функций (y – исходные данные, y_1 – линейная зависимость, y_2 – степенная зависимость, y_3 – квадратичная зависимость) (Comparison of empirical functions (y – initial data, y_1 – linear dependence, y_2 – power dependence, y_3 – quadratic dependence))

При проведении сравнительного анализа методов сглаживания особое внимание следует уделять качеству сглаживания в области базовой линии. Чем лучше приближена непиковая базовая линия, тем точнее будет ваш прогноз для пика. Размер обрабатываемой площади практически не зависит от того, как сглаживается площадь пика, поскольку все методы, основанные на скользящем средневзвешенном значении, оставляют площадь неизменной. Однако на сглаживание также в значительной степени влияет способ построения базовой линии [7; 8; 16].

Оказалось, что метод скользящего среднего, медианный фильтр имеют среднюю эффективность. А у фильтра Калмана и методов машинного обучения эффективность высокая.

По ограниченности: скользящее среднее размывает резкие изменения. Медианный фильтр характеризуется задержкой сигнала и сохранением ступенчатых шумов.

Основное преимущество сглаживания медианы, полученного после анализа, по сравнению со сглаживанием скользящей средней заключается в том, что результаты становятся более устойчивыми к выбросам. Если в данных есть выбросы, связанные с ошибками измерения, сглаживание с использованием медианы обычно приводит к более плавным или, по крайней мере, «более надежным» кривым по сравнению со скользящим средним с тем же окном.

Основным недостатком сглаживания медианы является то, что этот метод приводит к более неровным кривым без явных выбросов, чем сглаживание скользящей средней [6– 8; 16]. Тот же результат достигается, когда этот метод применяется к нашим данным. И этот метод не допускает использования весов, что также является его недостатком.

Метод скользящих средних основан на предположении, что при определении средних значений исключаются случайные отклонения, а при сглаживании фактические значения ряда заменяются средними значениями, которые характеризуют среднюю точку периода скольжения [16].

В фильтре Гаусса параметры требуют настройки, а фильтр Калмана требует модель процесса.

Методы машинного обучения требуют больших объемов данных для обучения.

По вычислительным затратам: высокие затраты потребуются при применении фильтра Калмана и методов машинного обучения, а низкие затраты – при применении скользящего среднего и медианного фильтра.

Сравнительный анализ по применимости: скользящее среднее применяется для сглаживания данных, устранения высокочастотного шума. Медианный фильтр используется для устранения выбросов, сглаживания данных. Фильтр Калмана применяется для фильтрации динамического шума, требует знания о системе. Для удаления сложного шума при наличии достаточного количества данных применяют методы машинного обучения.

Заключение

Фильтрация шума является важным этапом при обработке данных, полученных при низкотемпературном воздействии на биологической ткани. Выбор подходящего метода фильтрации должен быть основан на тщательном анализе характеристик шума и данных, а также на понимании преимуществ и ограничений каждого метода.

Оптимизация фильтрации шума при низкотемпературном воздействии будет способствовать повышению точности диагностики и лечения в здравоохранении, а также расширению возможности биологических исследований.

Полученные результаты в работе откроют новые возможности для развития применения низких температур в медицине, биологии, и появятся предпосылки для формирования новых научных направлений на стыке наук.

Дальнейшие исследования в этой области должны быть направлены на разработку новых и усовершенствование существующих методов фильтрации, с акцентом на специфические требования задач криобиологии и криотехнологии.