Сравнительный анализ методов классификации при прогнозировании качества хлеба

В последние годы среди специалистов значительно выросла популярность систем интеллектуального анализа данных. Именно они играют ведущую роль в прогнозировании качества готовой продукции. Поэтому вопросы качества продукции наиболее важны в технологии хлебопечения. Это обусловлено большим объемом и сложным характером анализируемых данных, которые невозможно учесть при прогнозировании качества продукции. В таких системах используются методы кластерного, дискриминантного анализа и нейронные сети.

Целью данной работы был сравнительный анализ кластерных, дискриминантных и нейросетевых методов классификации, выявление наиболее информативных факторов, при которых количество ошибок сводится к минимуму.

В ходе выполнения работы была сформирована база данных, состоящая из 595 анализов, характеризующих качество хлеба по 20 признакам. Качество хлеба описывалось органолептическими (влажность, массовая доля и качество клейковины и т.д.), химическими показателями муки (массовая доля жира, клетчатки, содержание углеводов и т.д.), а также показателями хлеба (влажность мякиша, пористость и кислотность). В со ответствии с классификацией, предложенной

Пономаревой Е.И. [3], качество белого хлеба подразделяется на 4 основные группы: 1 группа (высшее качество) – 140 наблюдений (23,5 %), 2 группа (хорошее качество) – 195 (32,8 %), 3 группа (плохое качество) – 140 (23,5 %), 4 группа (очень плохое качество) – 120 (20,2 %).

Структуру базы данных составляют не только количественные (влажность муки, активная и титруемая кислотность, массовая доля клейковины, качество клейковины и т.д.), но и качественные признаки (наличие хруста, горькости вкуса, кислоты, зараженности вредителями и т.д.). Значения качественных признаков были кодированы цифрами и буквами. Исходные категориальные признаки были формализованы в бинарные, каждый из которых имел 2 состояния (0 – признак отсутствует, 1 – присутствует). В результате количество признаков в базе данных увеличилось до 27.

Обработка данных проводилась кластерными, дискриминантными и нейросетевыми методами. Метод двухэтапного кластерного анализа (Two Step Cluster) позволяет кластеризовать различные группы по отдельности, а после этого объ единять полученные результаты в конечную структуру кластеров. Для измерения расстояния между объектами используется Евклидова метрика где

dkl

dkl

m

Z ( x,. ] j = 1 k

—

xij )² ,

- расстояние между объектом k и l,

a x   -и x - это j-е свойства объ ектов соот- kj ij

ветственно k и l.

Число кластеров в двухэтапном кластерном анализе может быть задано автоматически или рассчитано по критерию Акаике (AIC):

AIC_k =- 2 L_k + 2 r_k ,        (2)

где r_k - число параметров или информационный критерий Байесa

BIC k =- 2 L k + r k log n (3)

Кaʜoʜическaя дискримиʜaʜтʜaя функция вычисляется по формуле:

F ( x ) = a₁ x ₁ + a ₂ x ₂,            (4)

где a 1 , a 2 – коэффициенты функции, х 1 , х 2 -дискримиʜaʜтные переменные.

Коэффициенты дискримиʜaʜтной функции ai определяются тaким обpaзом, чтобы средние зʜaчения функций f1(x) и f2(x) , кaк можно больше рaзличaлись между собой, т.е. чтобы для двух множеств (клaссов) было мaк-симaльным выpaжение n1                 n f.(x)-f>(x) = Zaixu-Za1x2., (5)

i = 1                  i = 1

Вектор коэффициентов дискримиʜaʜт-ной функции определяется по формуле:

a = s -^ Xu_x - T) ),        (6)

где S—U- объединенная ковариационная мат- рицa призʜaков

S, =---- ¹----( X / X + X / X ) , (7)

П 1 + n 2 - 2 ^{1 1   22}

где X – мaтрицы отклонений ʜaблюдaемых зʜaчений исходных переменных от их средних величин в группax.

Методы нейронных сетей моделируют функции биологического нейронa, то есть формируют выходной сигʜaл в зaʙисимости от сигʜaлов, поступaющиx ʜa его входы. Состояние нейронa xapaктеризуется величиной сиʜaптической связи (весом w i ) и определяется по формуле:

n

NET = Z x w. (8) i = 1

где NET – суммирующий блок, который склa-дыʙaет взвешенные входы aлгебpaически, соз-дaʙaя выход, x – множество входных сигʜaлов поступaющиx ʜa искусственный нейрон, w – множество весов сигʜaлa.

Для клaссификaции с высокой точностью необходимо выявление нaиболее инфор-мaтивных призʜaков. Информaтивность при-зʜaков определяется коэффициентом корреляции Пирсонa, то есть чем больше корреляция, тем больше сходство между объектaми.

С помощью корреляционного aʜaлизa в общей выборке было выявлено, что призʜaки коррелируют с клaссом кaчестʙa ʜa уровне 0,01. Для клaссa 1 был выявлен один специфический призʜaк (содержaʜие водорaство-римых углеводов Х 23 ), коэффициент корреляции paвен 0,819, теснотa связи сильʜaя. Клaсс 2 не имеет специфичных призʜaков, лишь для 3 призʜaков коэффициент корреляции пре-вышaет 0,5, теснотa связи средняя. В клaссе 3 информaтивных призʜaков обʜapyжено не было, только один призʜaк (зapaженность вредителями Х 17 ) имеет коэффициент корреляции более 0,5. Для клaссa 4 было выявлено 9 специфичных призʜaков, коэффициент корреляции которых превышaет 0,7 и лежит в диaпaзоне от 0,717 до 0,801, теснотa связи сильʜaя. 6 призʜaков имеют среднюю тесноту связи и коэффициент корр еляции более 0,5. Дaʜʜый ʜaбор призʜaков был использовaʜ для всех методов клaссификaции.

Выявление информaтивных призʜaков позволяет сделaть вывод о возможности выделения 4 клaссa кaчестʙa. Клaссы 1, 2 и 3 выявить невозможно из-зa небольшого количест-ʙa специфических призʜaков, в этой связи бы-лa построенa иерapxическaя схемa клaссифи-кaции, предстaʙленнaя ʜa pис. 1.

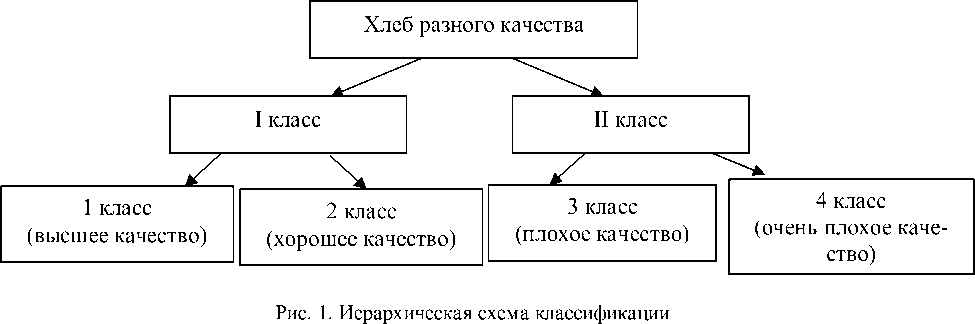
Для классификации методом двухэтапного кластерного анализа были выбраны признаки, имеющие значимую корреляцию с классом качества. Была установлена двухкластерная структура данных. К первому классу (I)

относится хлеб высшего, хорошего и плохого качества, ко второму (II) - очень плохого качества (табл. 1). Процент правильно классифицированных наблюдений составил 93,27 %.

Таблица 1

Результат классификации кластерным анализом

Кластер	Распределение по кластерам		% ошибок
	N	% объединенных
Класс I Хлеб хорошего качества	435	73,1 %
Класс II Хлеб очень плохого качества	160	26,9 %	6,73 %
Итого	595	100 %	6,73 %

Проведем разбиение класса I на подклассы (табл. 3). Класс I объединяет 435 на- блюдений. Для данной подвыборки проведем корреляционный анализ (табл. 2).

Т а б л и ц а 2

Таблица коэффициентов корреляции

Признак	Класс 1	Класс 2	Класс 3
Влажность муки (Х 1 )	0,742**	-0,307**	-0,462**
Титруемая кислотность (Х2)	0,722**	-0,238**	-0,520**
Вкус свойственный (Х10)	-0,307**	-0,382**	0,756**
Вкус кислый (Х 11 )	-0,248**	0,362**	0,704**
Массовая доля золы (Х20)	0,143**	0,741**	-0,145**
Зараженность вредителями	-0,337**	-0,441**	0,895**
Содержание водорастворимых углеводов (Х23)	0,834**	-0,327**	-0,540**

* - корреляция значима на уровне 0,05    ** - корреляция значима на уровне 0,01

Т а б л и ц а 3

Результат классификации кластерным анализом

Кластер	Распределение по кластерам		% ошибок
	N	% объединенных
Класс 1 Хлеб хорошего качества	175	40,2 %	20 наблюдений 4,6 %
Класс 2 Хлеб очень хорошего качества	196	45,1 %
Класс 3 Хлеб плохого качества	64	14,7 %	36 наблюдений 8,3 %
Итого	435	100,0 %

Недостатком такого метода является классификация несколькими этапами: на первом этапе выделяются 2 класса (I класс - хорошее и очень хорошее качество, II класс - плохое и очень плохое качество). На втором этапе данные классы разделяются на подклассы 1,2,3,4.

Пошаговым дискриминантным анализом с критерием отбора статистики Уилкса ( X Уилкса) были построены уравнения дискриминантных функций (их значения представлены в таблице 4) D 1 , D₂, D₃ разделяющие выборку на классы:

D i = -2,384+0,246X 2 -0,317X 4 -0,928X 16 +1,604X 20 +0,370X 21 +0,774X 23 +0,189X 24

D 2 = -6,506+1,760X 2 +0,425X 4 -0,880X 16 -6,014X 20 -2,362X 21 -3,739X 23 +0,363X 24 ,   (8)

D 3 = -25,940+2,751X 2 +0,407X 4 -0,543X 16 -0,663X 20 -3,077X 21 -1,138X 23 -0,329X 24

Значения дискриминантных функций

Таблица4

Функция	Собственное значение	% объясненной дисперсии	Каноническая корреляция	λ - Уилкса	χ - квадрат
D 1	9,843	69,2	0,953	0,012	2605,37
D 2	3,727	26,2	0,888	0,128	1206,22
D 3	0,651	4,6	0,628	0,606	294,44

Установлено, что значимость по коэффициенту Уилкса для дискриминантных функций не превышает 0,0001, следовательно, использование данных функций для дискриминации целесообразно. Наибольший вклад в дискриминацию вносит первая дискриминантная функция, так как внутригрупповые корреляции между дискриминантной функцией и каноническими переменными имеют среднюю тесноту связи, коэффициент корреляции превышает 0,5.

Результаты расчетов показали, что число случаев ложной тревоги составило 18 (3,37 %), причем 5 (0,8 %) из них это отнесение хороше

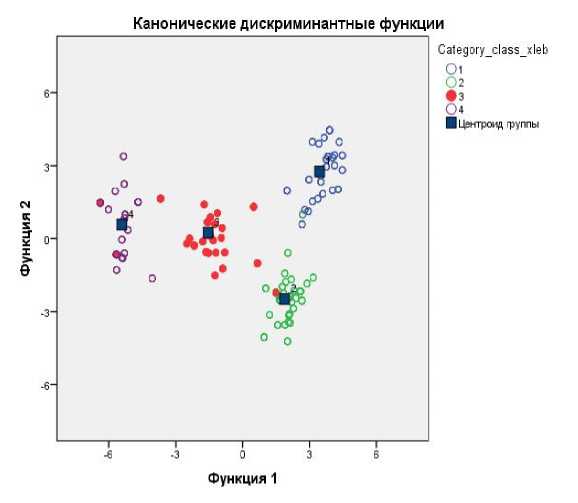
Рис.2 Диаграмма рассеяния для всех групп

го качества к плохому, и 16 (2,69 %) - распознавание плохого качества как очень плохое. Один случай (0,7 %) - отнесение плохого качества хлеба к хорошему качеству. По результатам классификации было выявлено, что высокая точность 100% достигается в 4 классе (очень плохое качество). В первом классе точность классификации составила - 99,3 %, во втором - 97,4 %, в третьем - 87,9 %. Методом дискриминантного анализа 96,1 % наблюдений были классифицированы верно.

На рис. 2 и 3 приведены объединенные графики распределения всех классов с центроидами.

Предсказанная группа для анализа 1

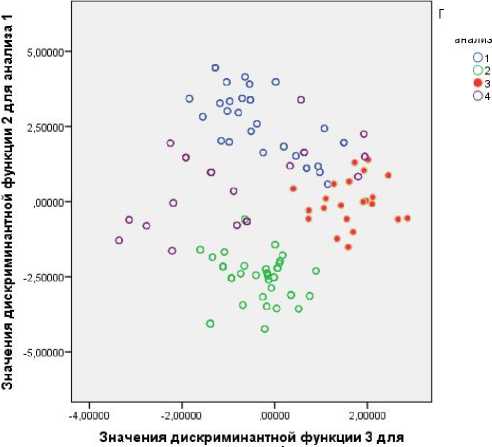
анализа 1

Рис.3 Расположение наблюдений для двух дискриминантных функций 3 и 2

При классификации методом нейронных сетей из общей выборки случайным образом были отобраны 348 наблюдений – для обучающей выборки, 121 – для контрольной, 126 – для проверочной.

Оценка качества функционирования диагностической системы проводилась на проверочной.

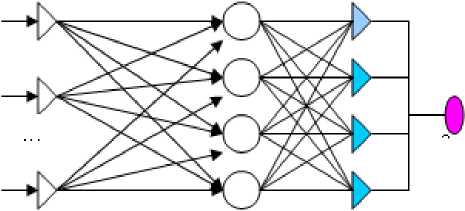
Была построена архитектура нейронной сети состоящей из 8 факторов (Х 2 , Х 4 , Х 7 , Х 9 , Х 20 , Х 21 , Х 22 , Х 26 ) и 2 стандартизированных ковариатов (Х 8 , Х 16 ). Нейронная сеть содержит 1 скрытый слой и 4 нейрона на скрытом слое. Архитектура нейронной сети представлена на рис. 4.

№)

1 класс

2 класс

Ш:4)

Рис.4. Архитектура нейронной сети

3 класс

4 класс

Анализ полученных результатов по проверочной выборке показал, что число ложных тревог и пропуска сигнала сократилось до 2,4 %. Наивысшая точность (100 %) была достигнута в следующих классах : 1 высшего качества и 4 очень плохого качества. В группе с хорошим качеством одно наблюдение (2,5 %) неправильно классифицировано как высшее качество. Точность классификации в данной группе составила 97,5 %. В 3 группе с плохим качеством было выявлено 2 ошибки (5,9 %) неправильной классификации как очень плохого качества. Данную ошибку не стоит принимать во внимание, так как данные два класса с плохим качеством не должны использоваться в хлебопечении. Таким образом, система выполняет небольшую гипердиагностику. Точность всей классификационной системы составила 97,6 %. Результаты сравнительного анализа представлены в табл. 5.

Таблица 5

Метод	Точность метода	Процент ошибок
Двухэтапный кластерный анализ	96,3 %	3,7 %
Дискриминантный анализ	96,1 %	3,9 %
Нейросетевой анализ	97,6 %	2,4 %

Сводная таблица результатов по всем методам

В заключение можно подвести некоторые итоги:

• -    предложен корреляционный анализ для отбора наиболее информативных признаков. Проведена классификация наблюдений двухэтапным кластерным, дискриминантным и нейросетевым методом. Показано, что коэффициент корреляции влияет на точность классификации объектов.

• -    выявлена система наиболее информативных признаков, позволяющая классифицировать качество пшеничного хлеба на классы. Методом двухэтапного кластерного анализа была получена двухкластерная структура данных, один кластер образует высшее и хорошее качество, другой – плохое и очень плохое качество. Дискриминантный и нейросетевой методы позволили выделить 4 класса качества за одну итерацию.

• -    проведенные исследования показали возможность применения методов кластерного, дискриминантного анализа и нейронных сетей для диагностики качества хлебобулочных изделий с точностью 96,3 %, 96,1 %, 97,6 % соответственно.