Сравнительный анализ методов нормализации контраста изображений

С появлением в мире технологий, способных обрабатывать визуальную информацию, появилась необходимость в улучшении качества изображений. Одна из важных характеристик изображения – его контрастность. Нормализация контраста помогает минимизировать влияние неоднородного освещения и улучшает результаты работы с изображениями. Например, многие алгоритмы компьютерного зрения, такие как распознавание объектов, детектирование границ и классификация, чувствительны к качеству изображения [1–3]. Для визуализации результатов работы алгоритмов используется язык программирования python версии 3.13 с использованием библиотек pywt, cv2 и numpy в среде разработки PyCharm ¹ .

Алгоритмы нормализации глобального контраста

Контраст изображения может быть количественно оценен на основе гистограммы распределения яркости [4]. Для изображений с высокой степенью контрастности харак-

1 Python 3.13.1 documentation // Python. URL: (дата обращения: 09.11.2024).

Дубровская Елена Андреевна магистрант, Национальный исследовательский университет «МЭИ», Москва. Сфера научных интересов: разработка программного обеспечения, информационные системы. Автор шести опубликованных научных работ.

терно равномерное распределение интенсивности светлых и темных пикселей; при этом пиксели концентрируются преимущественно вблизи экстремумов диапазона яркости. Гистограмма изображения, прошедшего процедуру нормализации контраста, как правило, охватывает весь динамический диапазон яркости, демонстрируя его более полное использование.

В данной работе будут рассмотрены методы нормализации контраста после преобразования аналогового сигнала в цифровой формат, поскольку именно на этом этапе появляется возможность эффективно корректировать параметры изображения с учетом его особенностей [5].

В работе описан алгоритм на основе накопительной функции, а также представлен линейный метод нормализации глобального контраста изображения.

Алгоритм на основе накопительной функции. Алгоритм, основанный на накопительной функции распределения (CDF), используется для нормализации глобального контраста изображения. Начальным шагом является формирование массива из 256 элементов, который представляет собой накопленное распределение уровней интенсивности пикселей в гистограмме изображения. Заполнение этого массива осуществляется путем суммирования значений гистограммы для каждого уровня интенсивности по формуле

CDF(i) = ^ h(i) ,                                 (1)

i = 0

Сравнительный анализ методов нормализации контраста изображений где CDF(i) – значение накопительной функции i-го уровня яркости, поступающее в массив; h(i) – значение гистограммы изображения i-го уровня яркости; i – значения яркости от 0 до 255 включительно.

На графике (см. Рисунок 1) отображена накопительная функция для изображения размера изображения N на M . На горизонтальной оси расположены значения от 0 до 255, характеризующие значения яркости i -го уровня, на вертикальной – накопительные значения CDF(i) , полученные при суммировании количества пикселей яркости i -го уровня по гистограмме.

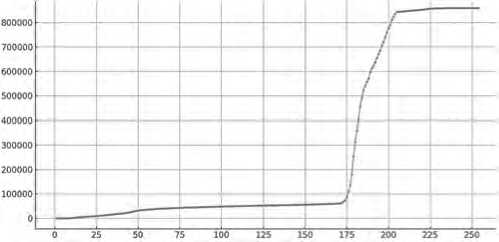
Рисунок 1. Накопительная функция Источник: составлено авторами

Наклон графика накопительной функции распределения характеризует скорость уве- личения суммарной интенсивности пикселей по мере продвижения по уровням яркости в исходной гистограмме. Чем более крутым является наклон графика на определенном интервале, тем большее количество пикселей с соответствующим уровнем яркости присутствует в изображении.

Следующим этапом является построение функции преобразования, которая на осно- ве накопительной функции переназначает исходные уровни яркости на новые значения, способствуя усилению общего контраста. Функция преобразования определяется по формуле

_f(i)= CDF(i)(L-1) NM

где f(i) – новое значение яркости значение, поступающее в массив трансформации;

CDF(i) – значение накопительной функции в точке интенсивности i ;

L – количество возможных уровней интенсивности (256 для 8-битных изображений);

N , M – длина и ширина оригинального изображения в пикселях.

В функции преобразования входные значения интенсивности пикселей отображаются по горизонтальной оси графика, тогда как соответствующие им выходные значения – новые уровни яркости после трансформации – располагаются по вертикальной оси. Оба набора значений лежат в диапазоне от 0 до 255.

На заключительном этапе алгоритма происходит замена интенсивности каждого пикселя изображения на новое значение, определенное функцией преобразования. Этот процесс итеративно проходит по всем компонентам пикселей, поэтому общее количество итераций соответствует размеру массива, содержащего данные этих компонент. Исходное значение яркости пикселя используется как индекс для доступа к массиву преобразования, после чего новое значение интенсивности записывается в результирующий массив. В итоге из этого массива формируется нормализованное изображение с улучшенными характеристиками яркости и контраста.

Однако данный метод может иметь ограничения при применении к изображениям с бимодальной гистограммой, имеющей два выраженных пика (см. Рисунок 2). В таких случаях, особенно когда один пик значительно превышает другой, функция преобразования может демонстрировать резкий градиент между пиками. Это может привести к чрезмерному усилению определенных уровней интенсивности и подавлению других, что вызывает искажение цвета, потерю деталей в ключевых областях и появление артефактов или шума [6]. Данная ситуация представлена на Рисунке 3.

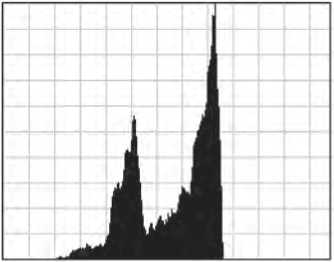
Рисунок 2. Бимодальная гистограмма

Источник : [7]

Рисунок 3. Оригинальные изображения: а – изображение без изменений; б – искаженное изображение с бимодальной гистограммой Источник:

Для предотвращения таких проблем может быть использован линейный алгоритм, который увеличивает контраст изображения, позволяя избежать появления артефактов.

Линейный алгоритм. Работа линейного алгоритма с постоянными коэффициентами имеет четыре этапа. На первом этапе по проценту от общего числа пикселей будут определяться пороговые значения x₁,x₂ . Для их нахождения устанавливаются пороги, соот-

Сравнительный анализ методов нормализации контраста изображений ветствующие определенному проценту ( a ) от общего числа пикселей [8]. Пороговое значение определяется по формуле threshold=NMa ,                                (3)

где threshold – число пикселей, при достижении которого устанавливаются пороговые значения с каждой стороны; a – выбранный процент (2,5 %); NM – ширина и высота изображения соответственно.

Пороговые значения x₁,x₂ определяются как уровни яркости, при которых накопленная сумма пикселей достигает threshold с начала и с конца гистограммы соответственно. Выбор метода установки порогов влияет на определение значимой части гистограммы, которая будет использована для построения массива трансформации. Метод установки порогов по проценту 5 от общего числа пикселей является наиболее распространённым из-за своей универсальности и снижения риска потери информации в важных областях гистограммы [9].

Второй этап – расчет коэффициентов угла наклона ( k ) и сдвига ( b ) после определения пороговых значений. Для определения этих коэффициентов используются линейные уравнения, необходимые для растяжения диапазона яркостей от a до полного диапазона [0,255]. Коэффициент k определяет угол между прямой и положительным направлением оси x , что влияет на контраст изображения. Система уравнений имеет вид

Г k₂X 1 +b₂=0 ,

[ k₂X 2 +b₂=255 ,

Г 255 k= , 2 X 2 -X 1

и - 255X 1 b= , _ 2 X 2 —X 1

где X1 – первое с начала значение яркости, которое больше среднего; X2 – первое с конца значение яркости, которое больше среднего; k2 и b2 – коэффициенты угла и сдвига соот- ветственно. Ограничение: X2 ^ X1.

Коэффициент b отвечает за сдвиг графика вдоль оси OY :

если b > 0, то график функции перемещается со сдвигом на b единиц вверх вдоль оси OY ;

если b < 0, то график функции перемещается со сдвигом на b единиц вниз вдоль оси OY .

От данного коэффициента будет зависеть степень яркости измененного изображения.

Третий этап – создание функции преобразования, которая заполняется значениями, полученными по линейной формуле с использованием коэффициентов:

f(i)=ki+b ,                                          (5)

где f(i) – новое значение интенсивности пикселя;

• k – коэффициент, который определяет наклон функции преобразования и влияет на контраст изображения;

• b – коэффициент, который отвечает за сдвиг по оси яркости, влияя на общую яркость результирующего изображения;

i – значение текущей яркости пикселя в диапазоне от 0 до 255.

На Рисунке 4 представлена функция преобразования, полученная с использованием линейного алгоритма.

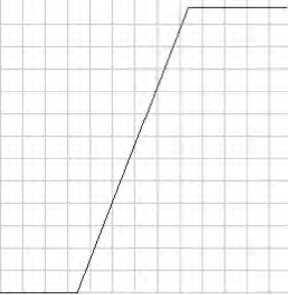
Рисунок 4. Функция преобразования, полученная с использованием линейного алгоритма Источник: составлено авторами.

Последний этап – трансформация компонент пикселей исходного изображения. Каждое значение яркости пикселя заменяется на соответствующее новое значение из массива преобразования. Этот процесс применяется ко всем компонентам пикселей (например, к красному, зеленому и синему каналам в RGB-изображениях) и аналогичен для различных алгоритмов нормализации [10]. На Рисунке 5 представлены результаты нормализации контраста изображения с помощью линейного алгоритма.

Рисунок 5. Результаты нормализации контраста изображения с помощью линейного алгоритма

К достоинствам линейного алгоритма можно отнести то, что он позволяет избежать резких перепадов между соседними значениями в массиве преобразования, что способствует более плавной нормализации изображения без существенных искажений цвета.

Ниже представлена сравнительная Таблица, отображающая оценку яркости и контраста изображений по трем методам глобальной оценки контраста. Оценки даны для оригинального изображения (см. Рисунок 3, а ), нормализованного изображения с помощью алгоритма на основе накопительной функции (CDF) (см. Рисунок 3, б ) и с помощью линейного алгоритма (LIN) (см. Рисунок 5). Оценки контраста рассчитаны методами RMS-контраста, энтропийного контраста и контраста по диапазону [11].

Сравнительный анализ методов нормализации контраста изображений

Таблица

Сравнительная характеристика оценки контраста для оригинальных изображений

Метод оценки	Рисунок 3, а , ORIG	Рисунок 3, б , CDF	Рисунок 5, LIN
Яркость	131	128	161
RMS-контраст	31	72	77
Энтропийный контраст	9,73	13,25	11,84
Контраст по диапазону	0,853	0,977	0,997

Источник: составлено авторами.

По результатам, приведенным в Таблице, можно заметить, что при оценке контраста методом RMS и контрастом по диапазону наибольшее значение у изображения, нормализованного с помощью линейного алгоритма, которое не имеет артефактов. При оценке энтропийным контрастом наибольшее значение у изображения, нормализованного с помощью алгоритма на основе CDF. Однако высокая оценка по энтропийному контрасту не всегда коррелирует с лучшим визуальным качеством изображения, так как артефакты увеличивают разнообразие и равномерность распределения интенсивностей пикселей, что повышает энтропию изображения и, следовательно, энтропийный контраст [11–14].

Из двух описанных методов выбор сделан в пользу линейного алгоритма за счет его универсальности. Представленные методы нормализации контраста изображения наиболее эффективны с точки зрения вычислительных ресурсов и времени. Результаты таких алгоритмов более предсказуемыми, так как они основаны на фиксированных математических формулах и алгоритмах. Эти методы применяют заранее определенные операции к пикселям изображения, не изменяясь в зависимости от данных, что приводит к меньшей универсальности. Это означает, что выбранные методы будут давать лучший результат нормализации контраста в случае подбора каждого алгоритма для определенной задачи.